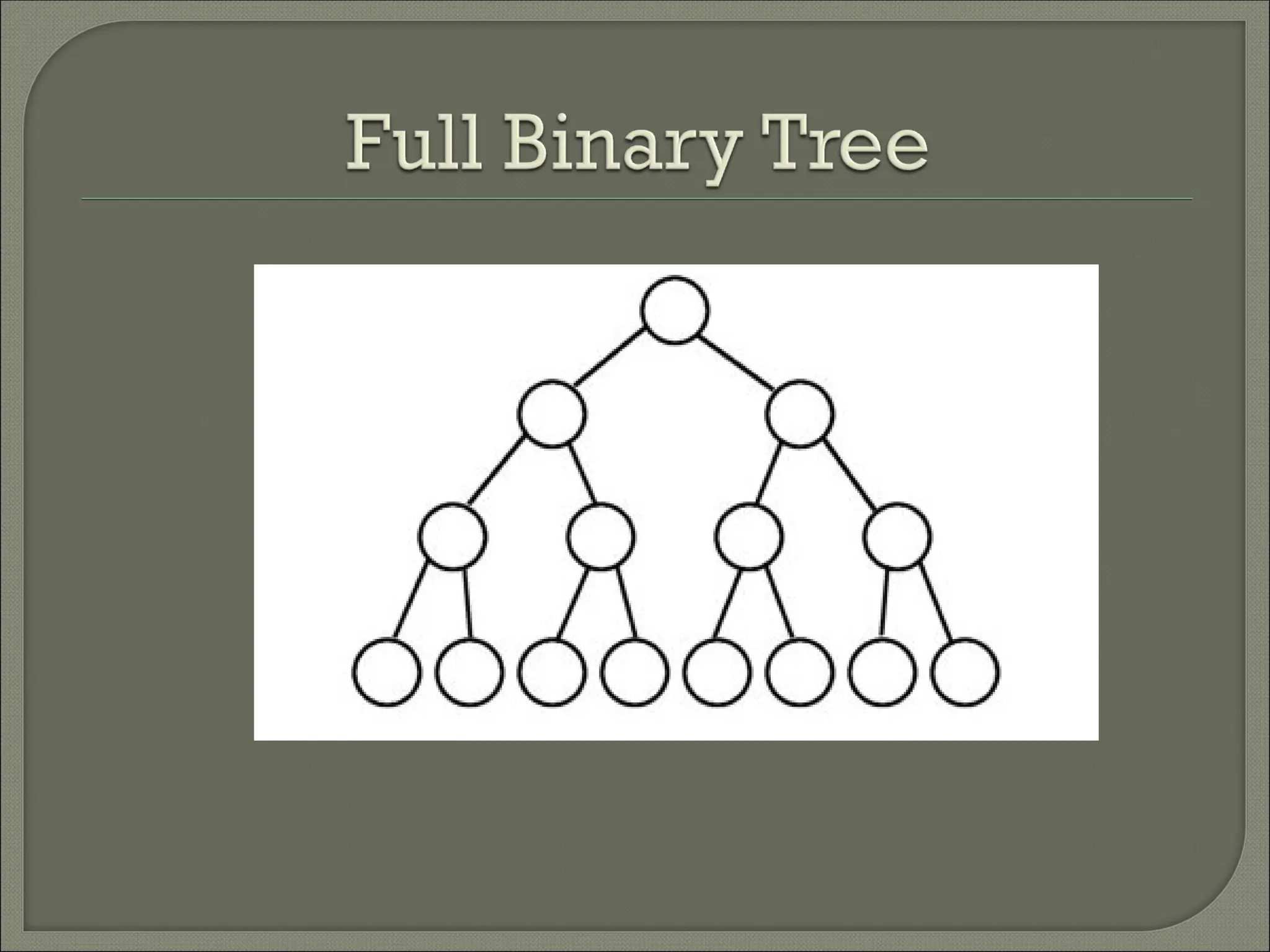
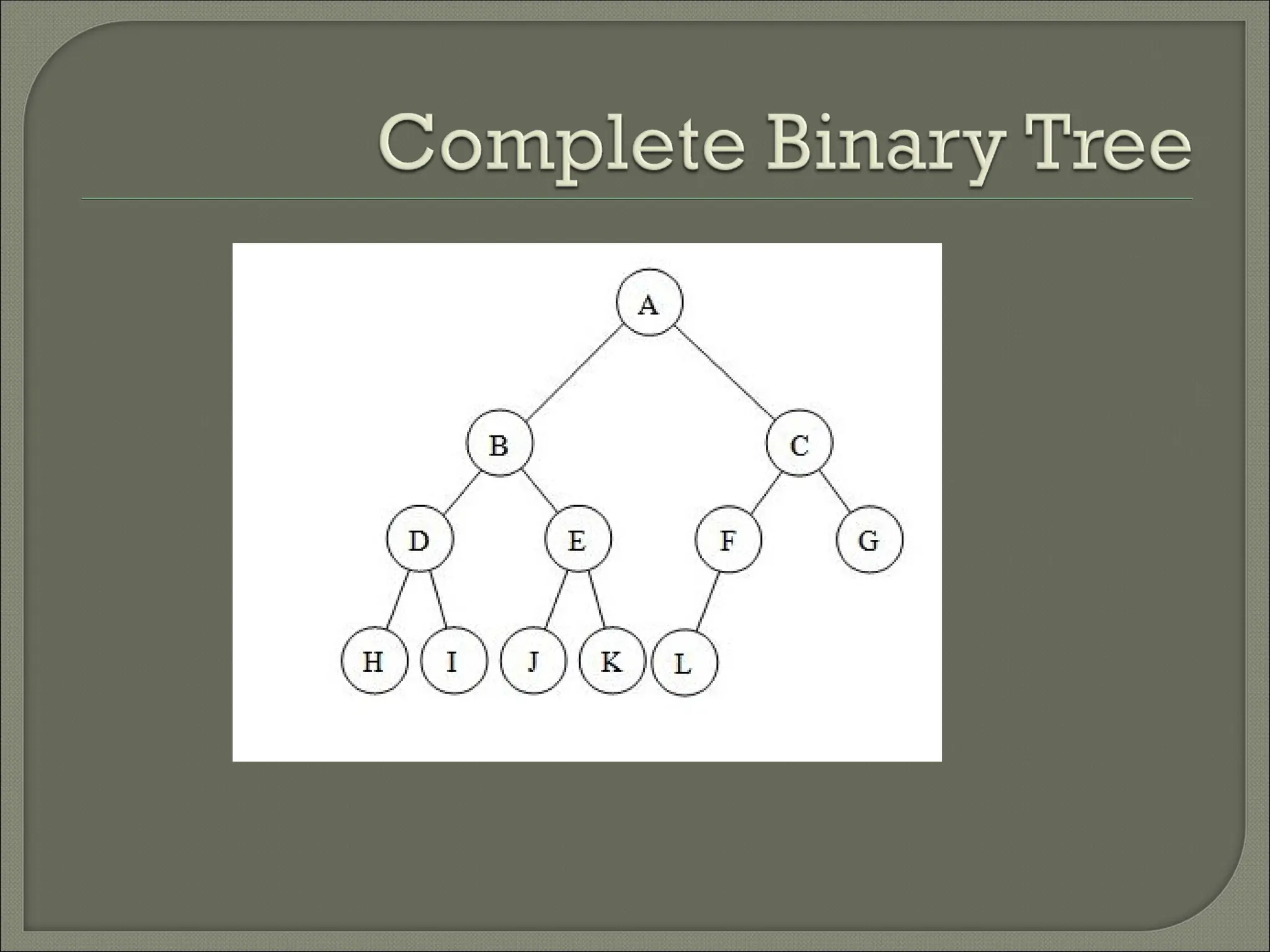
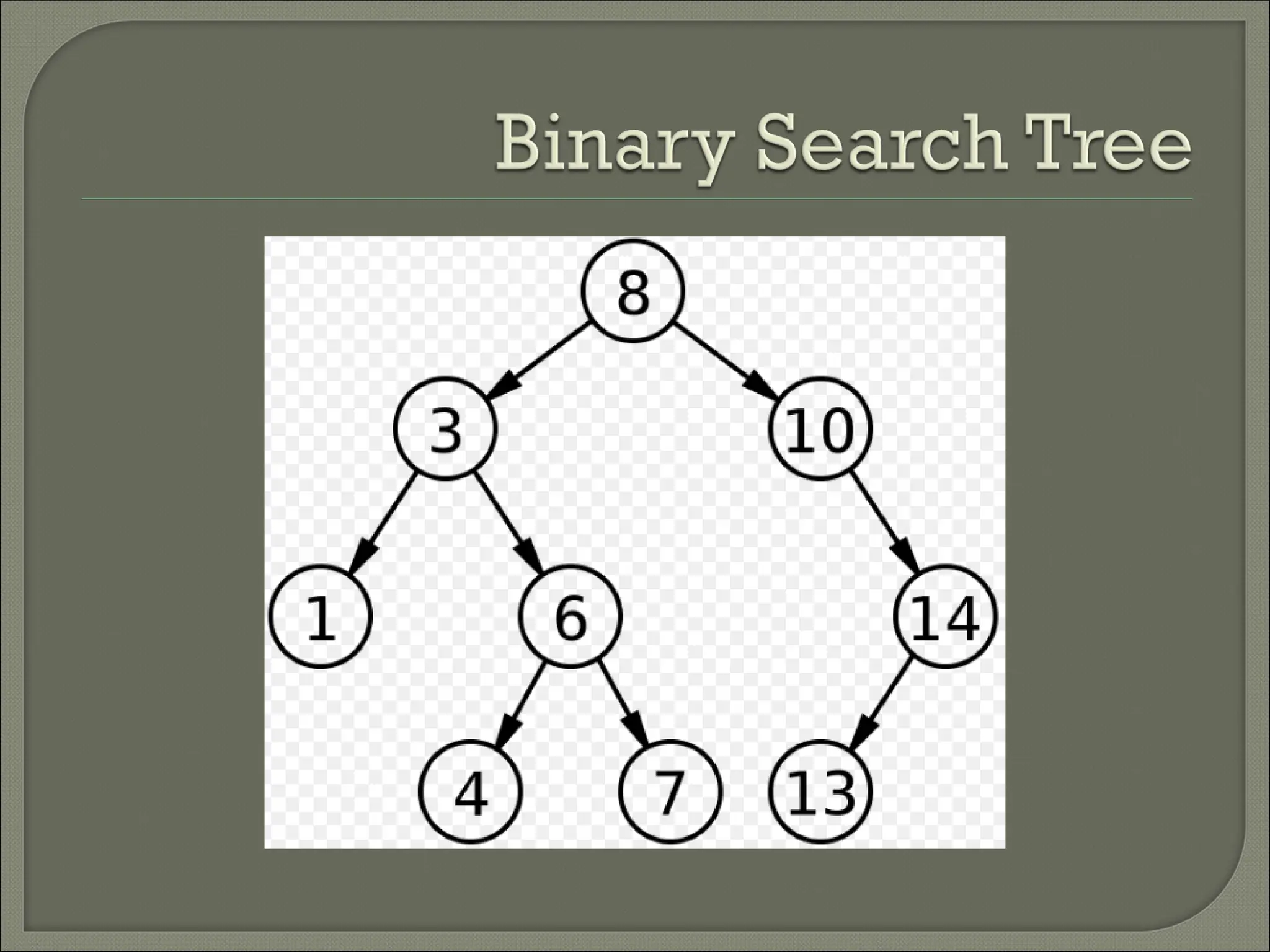
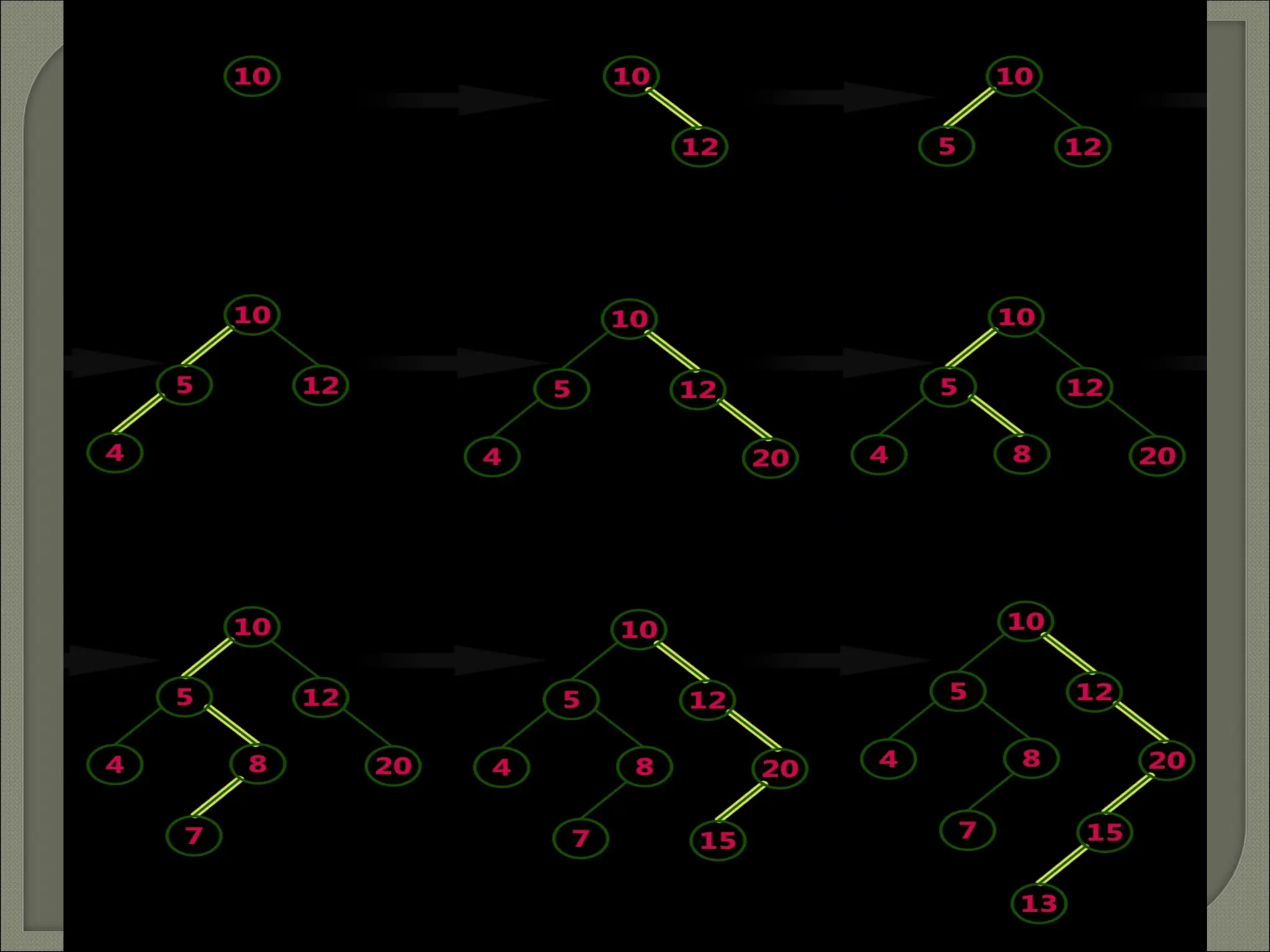
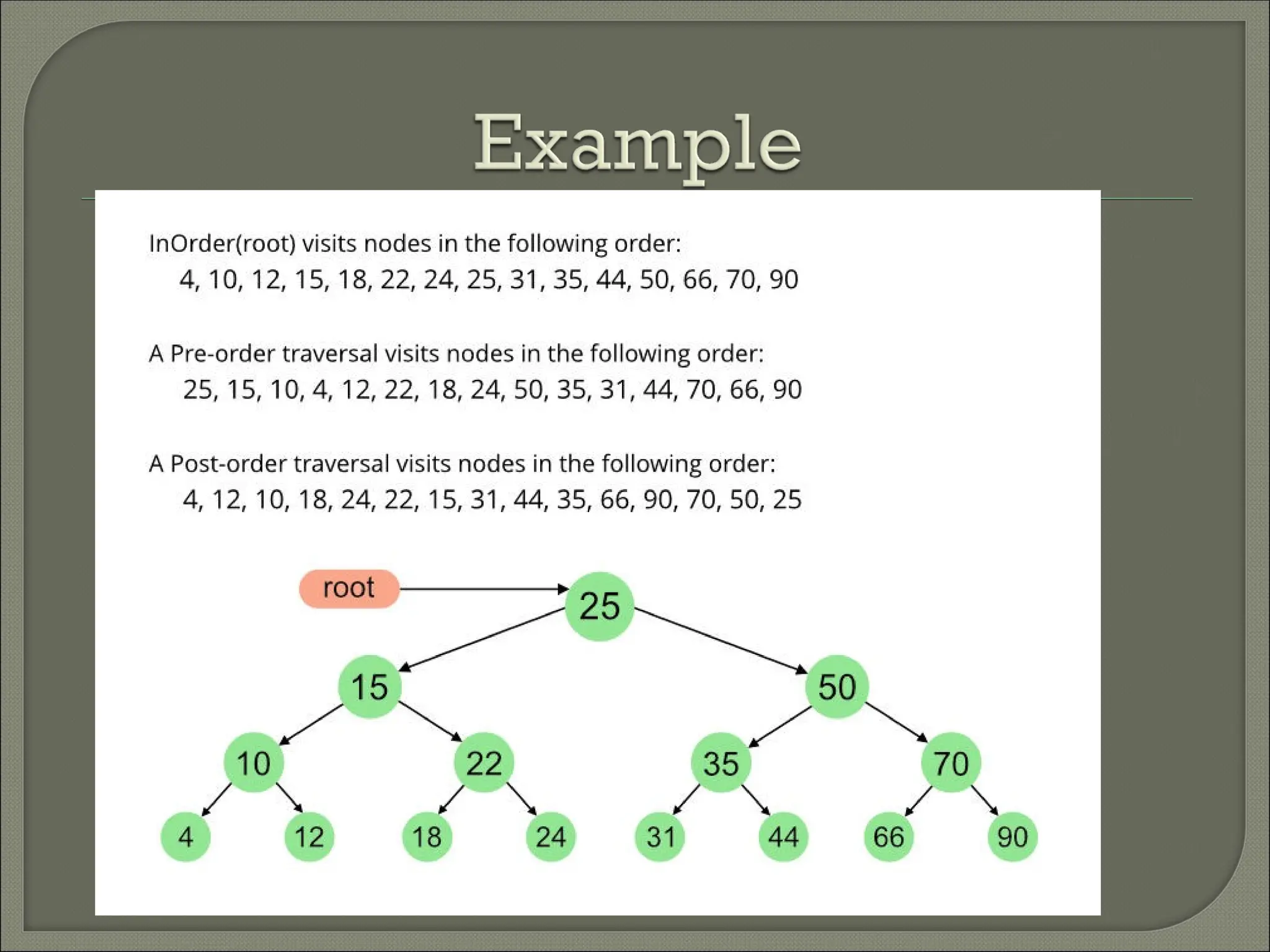
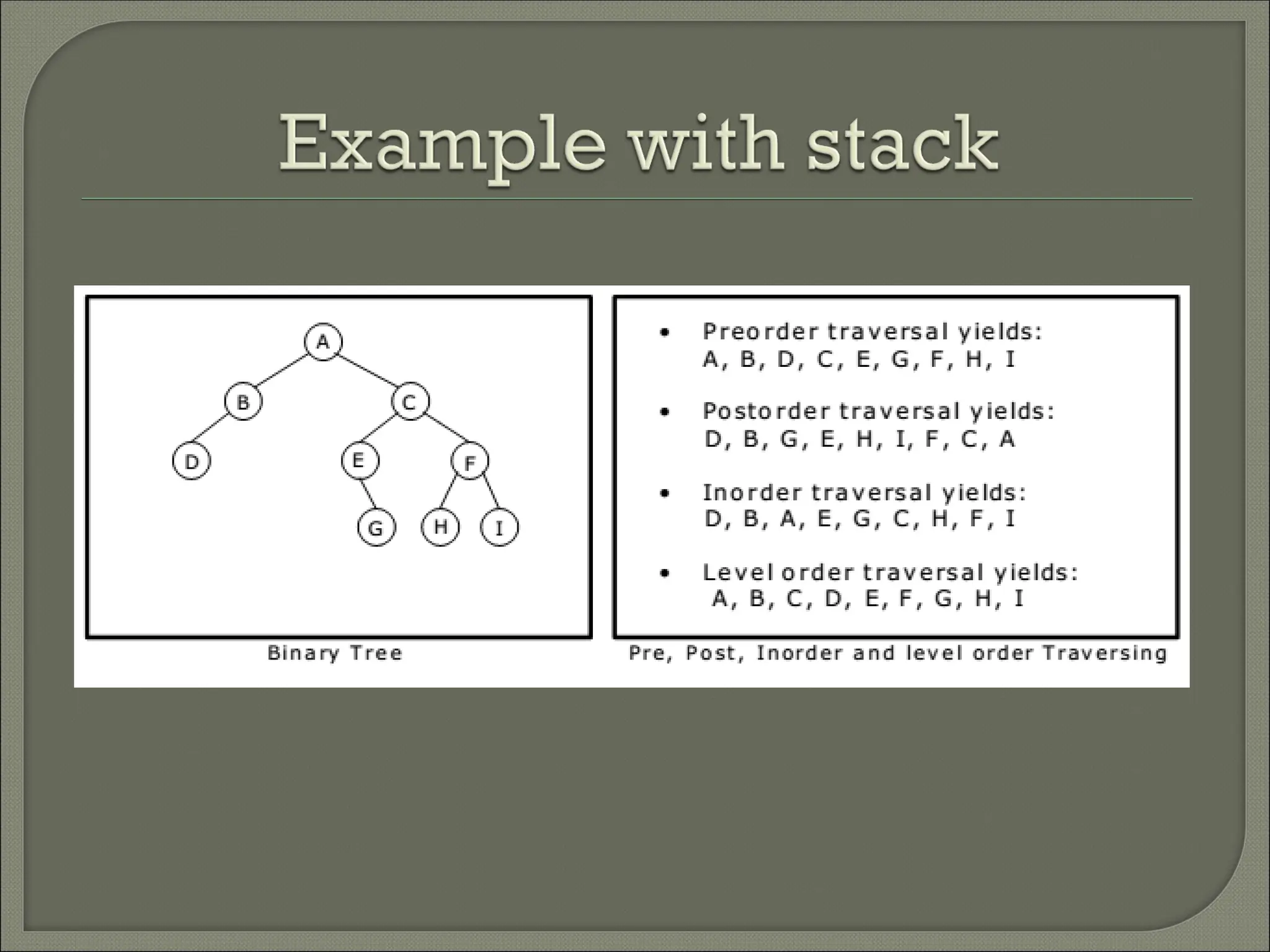
The document outlines the characteristics and operations of binary trees, including full and complete binary trees. It details the processes for searching, inserting, and deleting nodes within a binary search tree, providing step-by-step instructions for each operation. Additionally, it illustrates in-order, pre-order, and post-order tree traversals along with a sequence for constructing a binary search tree.