Download as PDF, PPTX
Uploaded byMohammad Tawfik
Introduction to Numerical Analysis
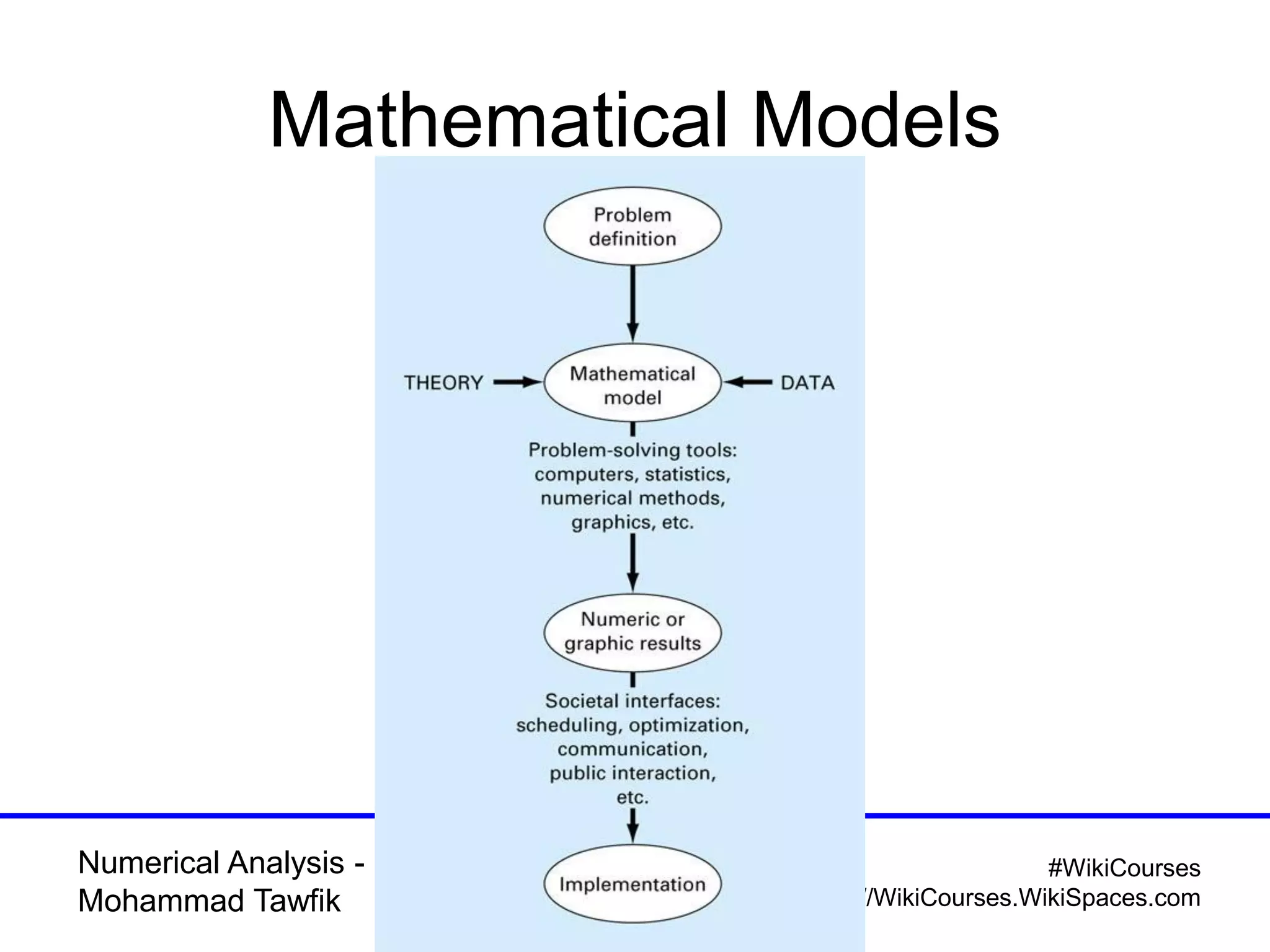
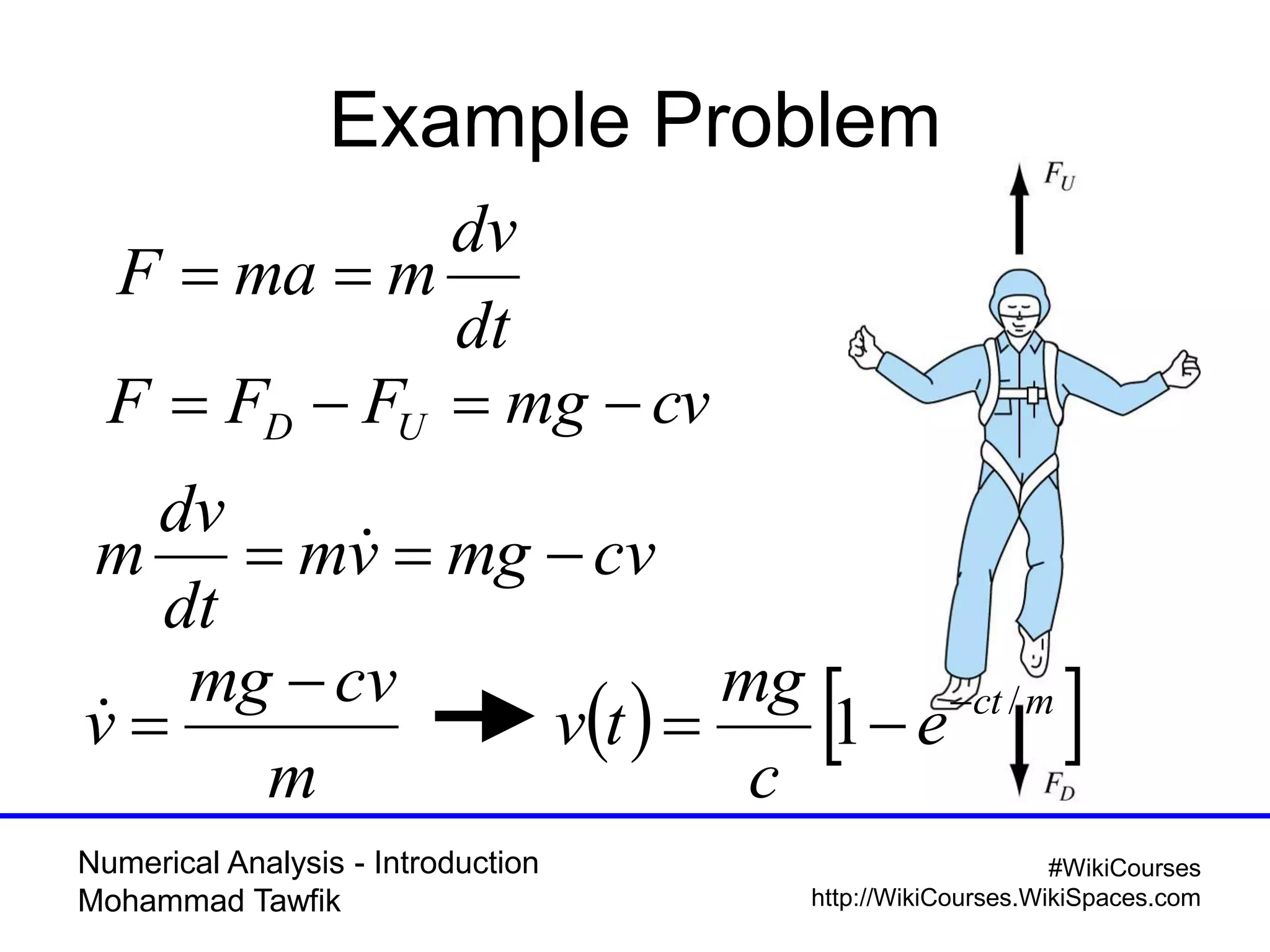
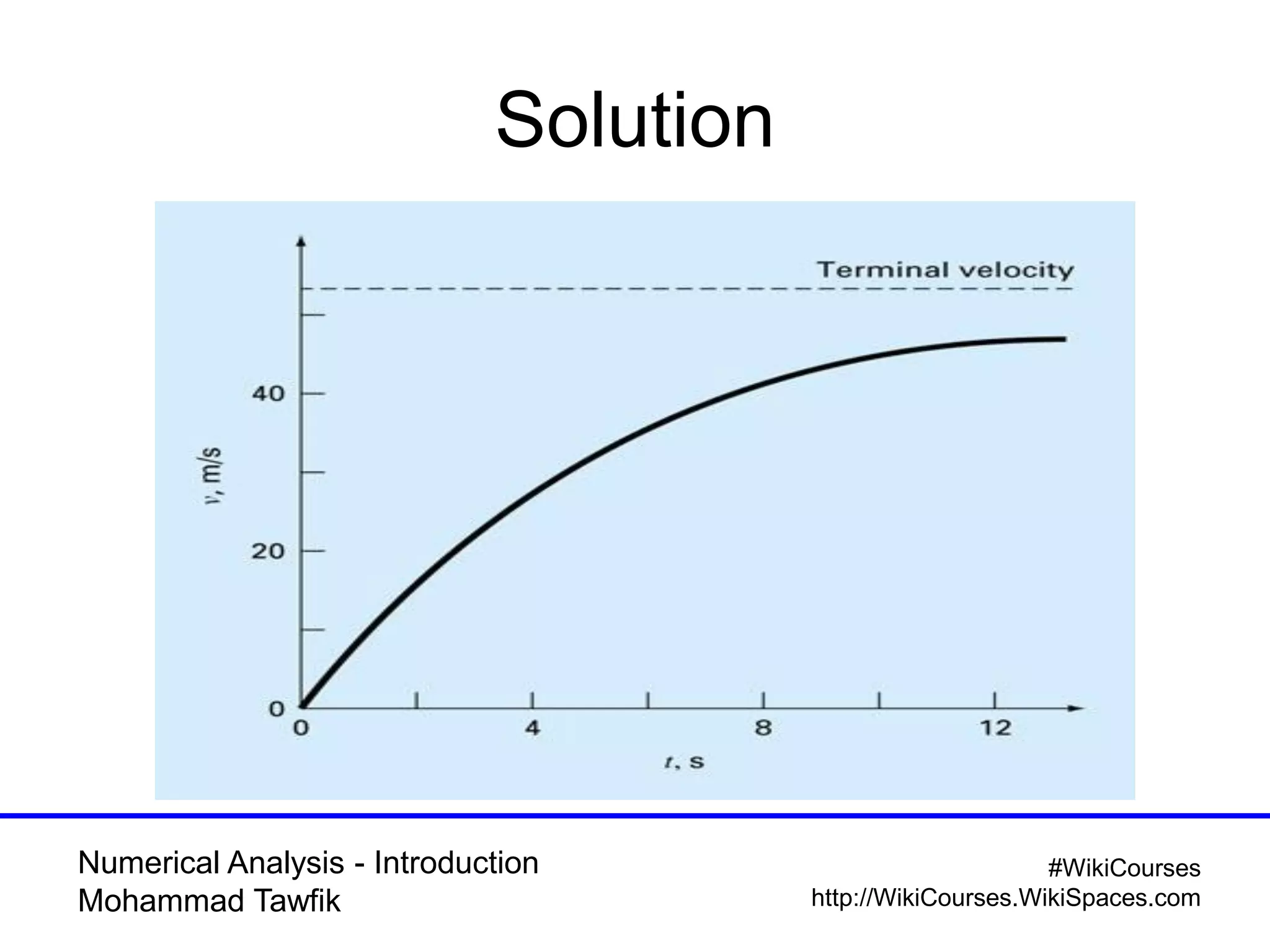
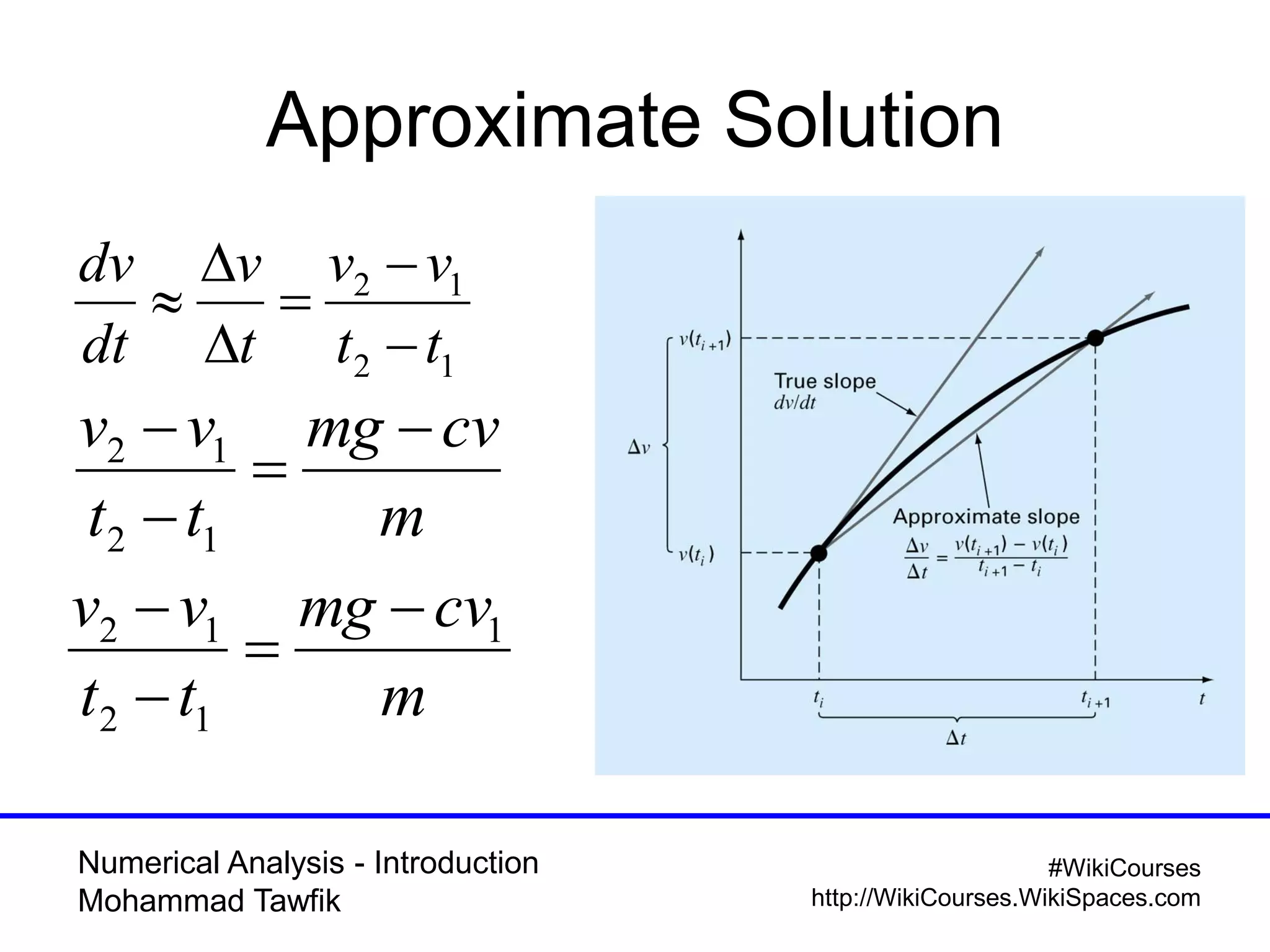
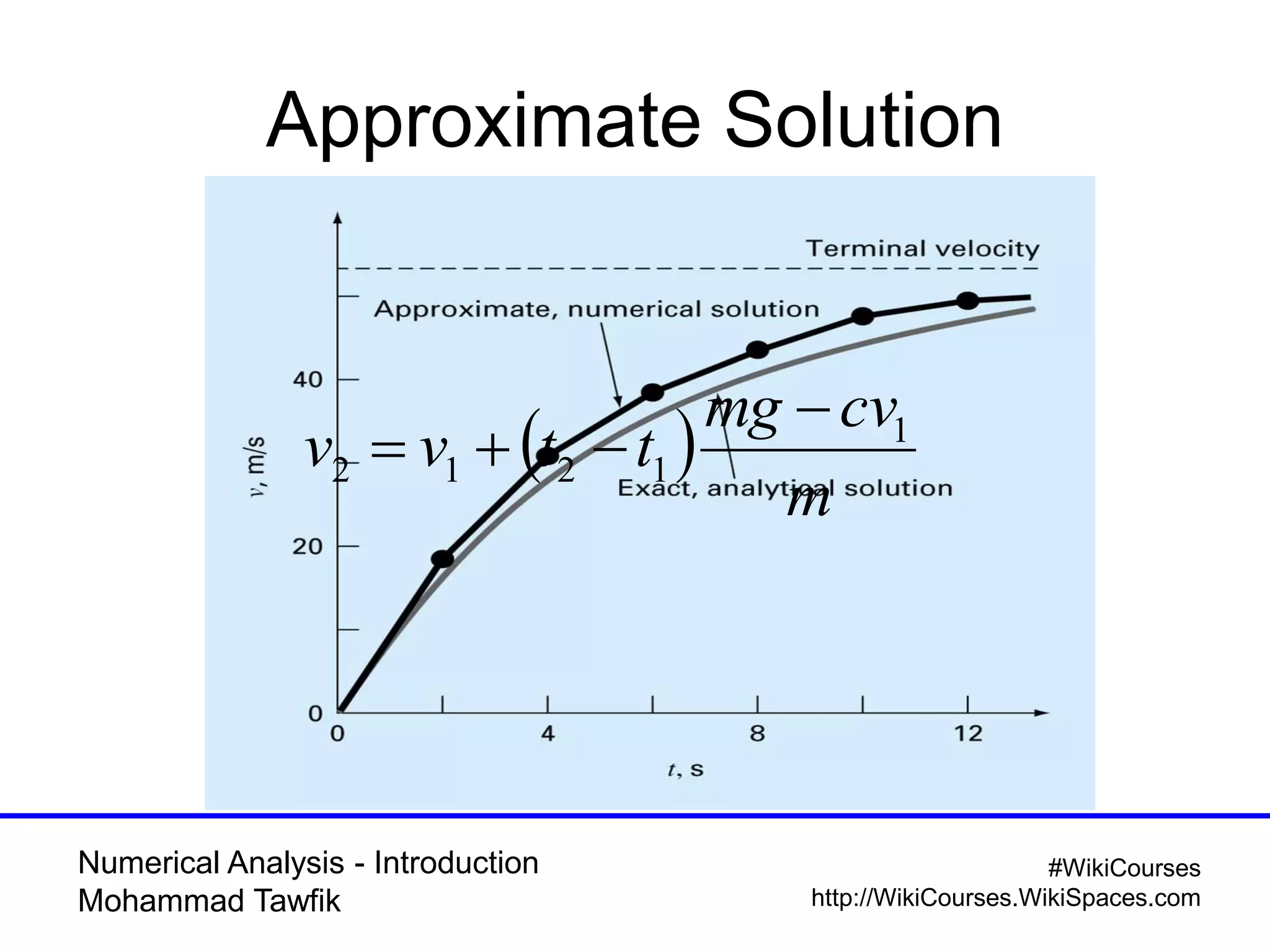
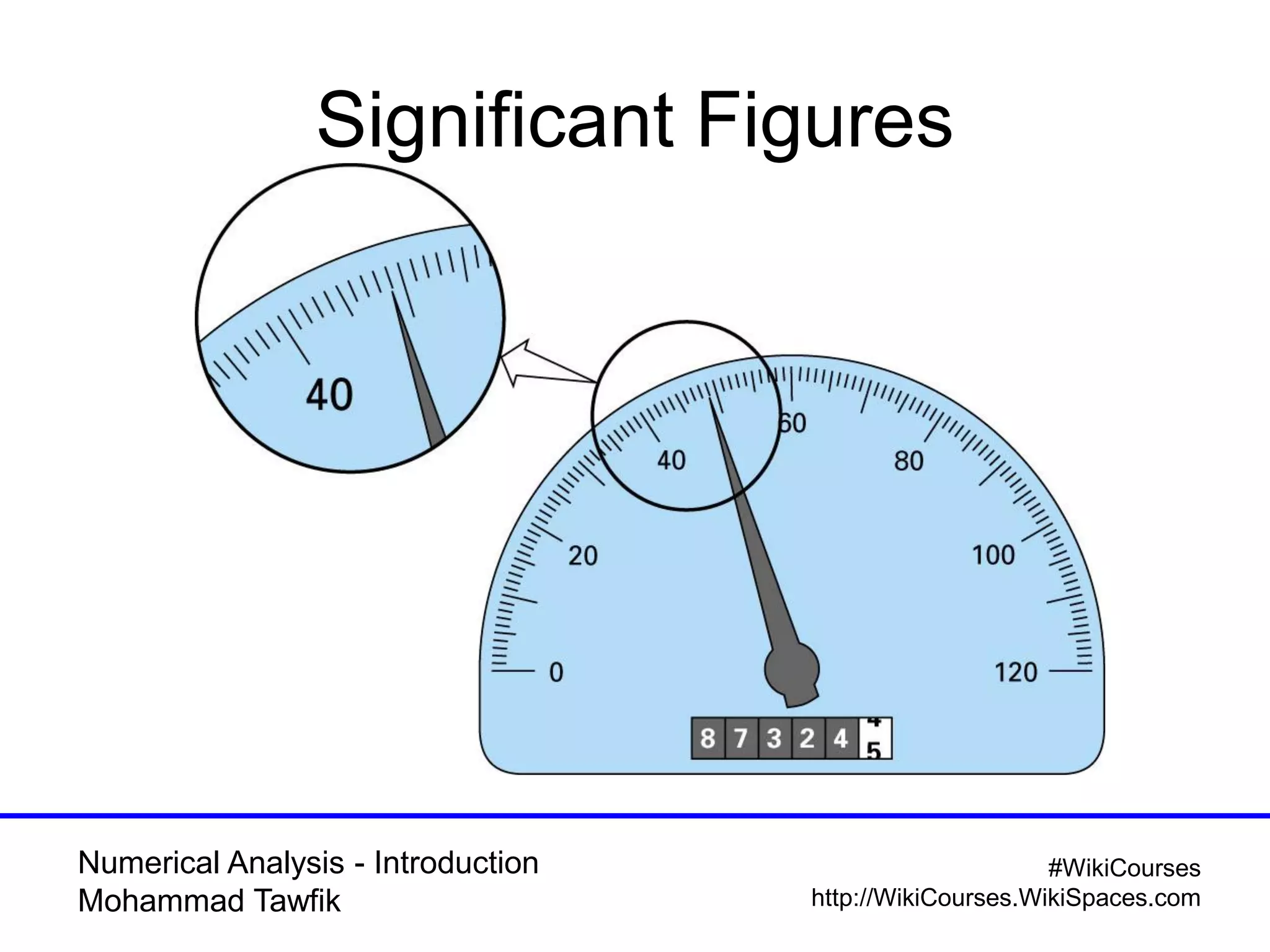
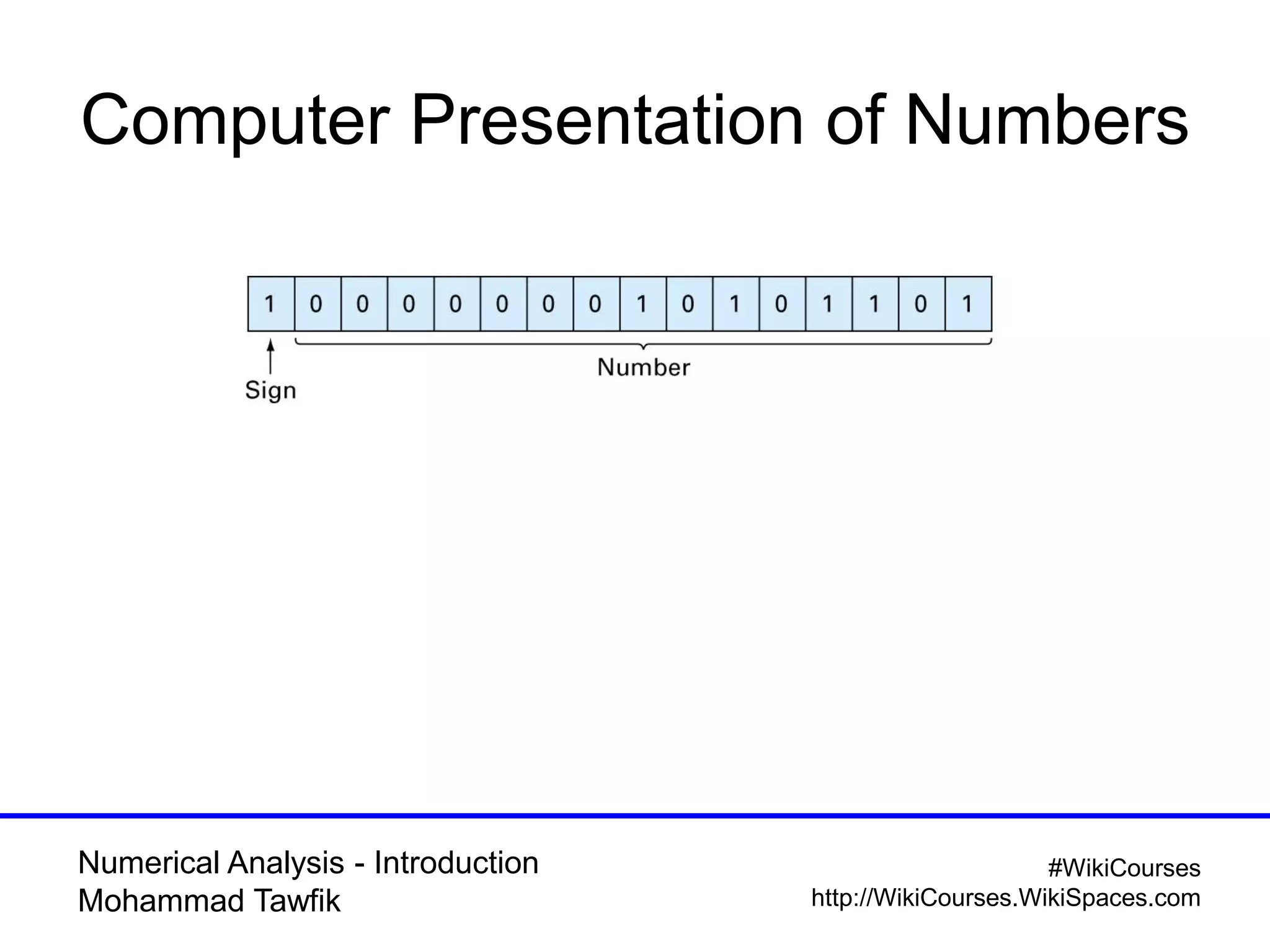
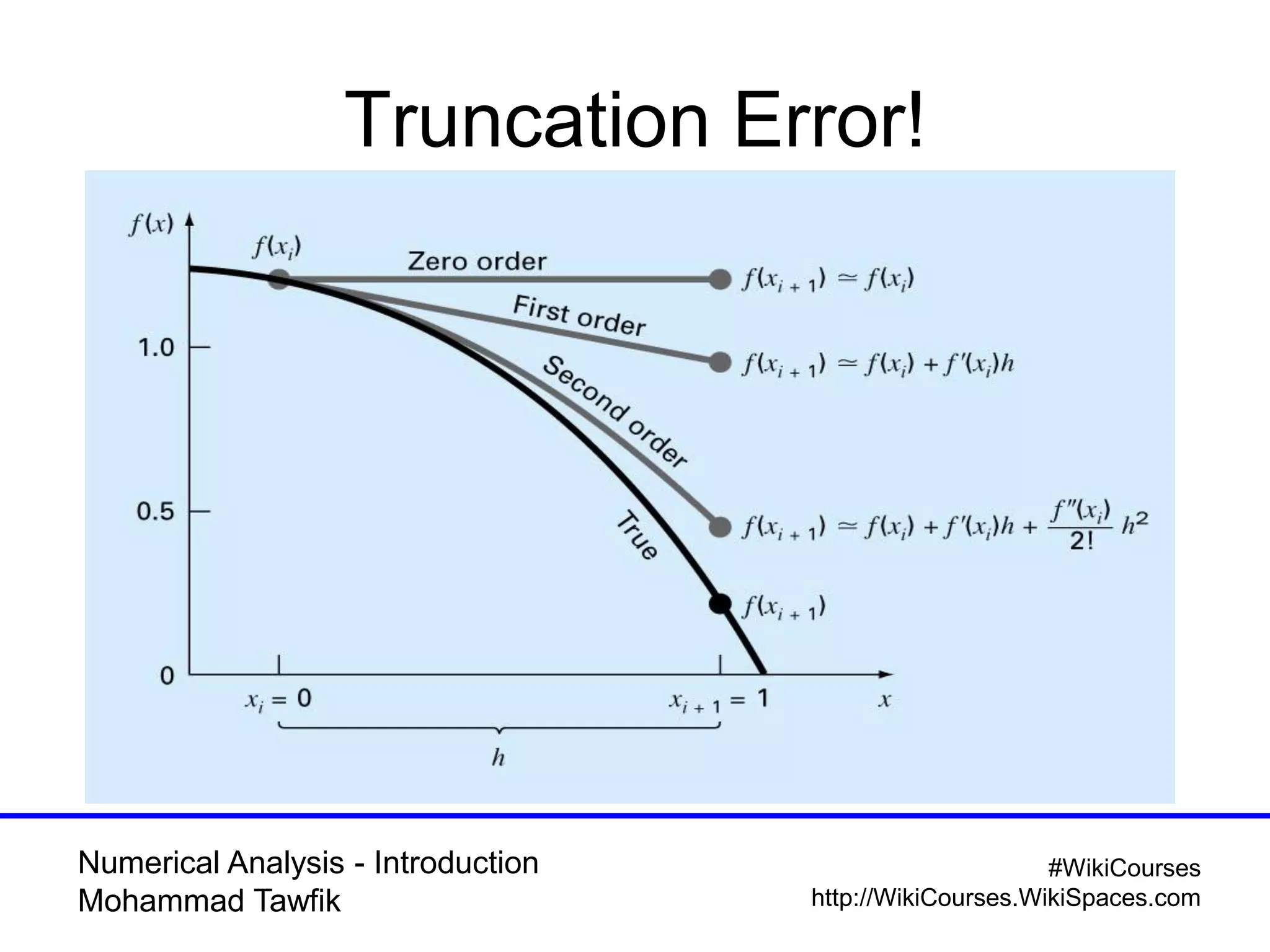
The document provides an introduction to numerical analysis, highlighting its necessity in solving complex mathematical problems and developing new techniques. It discusses various types of errors, including truncation, round-off, and model errors, and emphasizes the importance of accuracy and precision in numerical solutions. Additionally, it outlines the limitations of computer representations of numbers and the significance of approximation in numerical methods.
Introduction to Numerical Analysis
- 1. Numerical Analysis -Introduction Mohammad Tawfik #WikiCourses http://WikiCourses.WikiSpaces.com Numerical Analysis An Introduction
- 2. Numerical Analysis -Introduction Mohammad Tawfik #WikiCourses http://WikiCourses.WikiSpaces.com References • Steven Chapra and Raymond Canale, "Numerical Methods for Engineers," 5th editions, ISBN 0-07-123140-4
- 3. Numerical Analysis -Introduction Mohammad Tawfik #WikiCourses http://WikiCourses.WikiSpaces.com Numerical Methods
- 4. Numerical Analysis -Introduction Mohammad Tawfik #WikiCourses http://WikiCourses.WikiSpaces.com Why Numerical? • Ignorance • Readily Available Packages • Need to Develop New Techniques • Good use of your computer! • Re-Understand Mathematics
- 5. Numerical Analysis -Introduction Mohammad Tawfik #WikiCourses http://WikiCourses.WikiSpaces.com Mathematical Modeling & Engineering Solutions
- 6. Numerical Analysis -Introduction Mohammad Tawfik #WikiCourses http://WikiCourses.WikiSpaces.com Mathematical Models
- 7. Numerical Analysis -Introduction Mohammad Tawfik #WikiCourses http://WikiCourses.WikiSpaces.com Example Problem dt dv mmaF cvmgFFF UD cvmgvm dt dv m m cvmg v mct e c mg tv / 1
- 8. Numerical Analysis -Introduction Mohammad Tawfik #WikiCourses http://WikiCourses.WikiSpaces.com Solution
- 9. Numerical Analysis -Introduction Mohammad Tawfik #WikiCourses http://WikiCourses.WikiSpaces.com Approximate Solution 12 12 tt vv t v dt dv m cvmg tt vv 12 12 m cvmg tt vv 1 12 12
- 10. Numerical Analysis -Introduction Mohammad Tawfik #WikiCourses http://WikiCourses.WikiSpaces.com Approximate Solution m cvmg ttvv 1 1212
- 11. Numerical Analysis -Introduction Mohammad Tawfik #WikiCourses http://WikiCourses.WikiSpaces.com Approximation and Round-Off Errors
- 12. Numerical Analysis -Introduction Mohammad Tawfik #WikiCourses http://WikiCourses.WikiSpaces.com Errors! • Round-off errors are due to the fact that the computers present numbers in as a finite number of bits and bytes! • Truncation Errors are errors that emerge from the approximation of the mathematical model • Model errors are due to the fact that the mathematical model usually is an approximation of the physical reality!
- 13. Numerical Analysis -Introduction Mohammad Tawfik #WikiCourses http://WikiCourses.WikiSpaces.com Significant Figures
- 14. Numerical Analysis -Introduction Mohammad Tawfik #WikiCourses http://WikiCourses.WikiSpaces.com Accuracy and Precision • Accuracy how close your solution is • Precision is how close your repetition of the solution are!
- 15. Numerical Analysis -Introduction Mohammad Tawfik #WikiCourses http://WikiCourses.WikiSpaces.com Error Definition • True Error • True Relative Error • Approximate Error ionApproximatvalueTrueEt valueTrue Et t ionApproximatCurrent ApproxPastionApproximatCurrent a .
- 16. Numerical Analysis -Introduction Mohammad Tawfik #WikiCourses http://WikiCourses.WikiSpaces.com Round-off Errors 210 10*210*510*3253 21 10*510*225.0 4 1 ...10*310*310*310*3 ...33333.0 3 1 4321
- 17. Numerical Analysis -Introduction Mohammad Tawfik #WikiCourses http://WikiCourses.WikiSpaces.com Computer Presentation of Numbers
- 18. Numerical Analysis -Introduction Mohammad Tawfik #WikiCourses http://WikiCourses.WikiSpaces.com When numbers are too small!
- 19. Numerical Analysis -Introduction Mohammad Tawfik #WikiCourses http://WikiCourses.WikiSpaces.com Truncation Errors
- 20. Numerical Analysis -Introduction Mohammad Tawfik #WikiCourses http://WikiCourses.WikiSpaces.com Taylor’s Expansion ... !2 ''' 2 0 0000 xx xfxxxfxfxf 3 2 000 !2 ''' hO h xfhxfxfxf
- 21. Numerical Analysis -Introduction Mohammad Tawfik #WikiCourses http://WikiCourses.WikiSpaces.com Truncation Error!
- 22. Numerical Analysis -Introduction Mohammad Tawfik #WikiCourses http://WikiCourses.WikiSpaces.com Conclusion • We need the numerical methods to solve problems that do not have a solution or have a complex mathematical solution • Errors have different sources: Truncation, round off, and model errors • Error is evaluated using approximate solutions