In [11]:
# invisible lines = open("img_resolution.txt").readlines() resolution = lines[0].strip() if resolution != "default": import matplotlib as mpl mpl.rcParams['figure.dpi'] = int(resolution)


Matplotlib Tutorial: Achsen und Skalenteilung


Achsenverschiebungen und Achsenbezeichnungen

spines

In Matplotlib werden die Achsen als "spines" bezeichnet. Das englische Wort "spine" bezeichnet normalerweise das Rückgrat oder die Wirbelsäule des menschlichen Skeletts. Es kann aber auch für die Stacheln eines Kaktus stehen. Im Bild haben wir ein Bild mit Kakteenstacheln soweit verändert, dass sie Ähnlichkeit mit einem Brustkorb haben. "spines" bezeichnen in Matplotlib die Linien, welche die Achsen-Markierungen verbinden unter Berücksichtigung des Datenbereichs. Im Deutschen sprechen wir von Achsen.

Wir demonstrieren im Folgenden, wie wir die Achsen ("spines") an beliebige Stellen verschieben können.

Bevor wir damit beginnen können, führen wir die gca-Funktion ein. Diese Funktion liefert eine Referenz auf die aktuelle Plotinstanz bzw. Figur zurück.

Wir können zum Beispiel plt.gca(projection='polar') aufrufen, um die aktuellen Polar-Achsen zu erhalten.

In [12]:
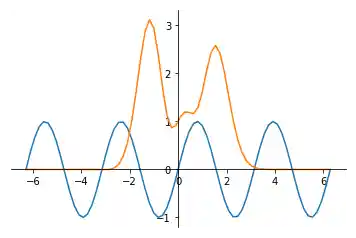
import numpy as np import matplotlib.pyplot as plt X = np.linspace(-2 * np.pi, 2 * np.pi, 70, endpoint=True) F1 = np.sin(2* X) F2 = (2*X**5 + 4*X**4 - 4.8*X**3 + 1.2*X**2 + X + 1)*np.exp(-X**2) # aktuellen Plot zuweisen: ax = plt.gca() # Obere und rechte Achse unsichtbar werden lassen: ax.spines['top'].set_color('none') ax.spines['right'].set_color('none') # Untere Achse auf die y=0 Position bewegen: ax.xaxis.set_ticks_position('bottom') ax.spines['bottom'].set_position(('data',0)) # Linke Achse auf die Position x == 0 bewegen: ax.yaxis.set_ticks_position('left') ax.spines['left'].set_position(('data',0)) plt.plot(X, F1) plt.plot(X, F2) plt.show()
matplotlib_spines_und_ticks: Graph 0

Matplotlib hat bis jetzt -- in allen vorangegangenen Beispielen -- automatisch den Abstand der Punkte auf der Achse ermittelt. In unserem vorigen Beispiel haben wir gesehen dass die X-Achse mit -8, -6. -4, -2, 0, 2, 4, 6, 8 nummeriert war, während die Y-Achse mit -2.0, -1.5, -1.0, -0.5, 0, 0.5, 1.0, 1.5, 2.0 beschriftet ist.

xticks ist eine Methode, die für das Abfragen und Verändern von Tick-Positionen und Beschriftungen benutzt werden kann. Das Gleiche gilt für die Methode yticks.

In [13]:
ax = plt.gca() locs, labels = plt.xticks() print(locs, labels) locs, labels = plt.yticks() print(locs, labels) 
[0. 0.2 0.4 0.6 0.8 1. ] <a list of 6 Text xticklabel objects> [0. 0.2 0.4 0.6 0.8 1. ] <a list of 6 Text yticklabel objects>
matplotlib_spines_und_ticks 2: Graph 1

Wie bereits erwähnt, kann xticks ebenso dazu verwendet werden, um die Position der Ticks auf der X-Achse zu verändern:

In [14]:
plt.xticks( np.arange(10) ) locs, labels = plt.xticks() print(locs, labels) 
[0 1 2 3 4 5 6 7 8 9] <a list of 10 Text xticklabel objects>
matplotlib_spines_und_ticks 3: Graph 2

Jetzt verändern wir sowohl die Position als auch die Beschriftung der Ticks auf der X-Achse:

In [15]:
plt.xticks( np.arange(4), ('Berlin', 'London', 'Hamburg', 'Toronto') )
Out[15]:
([<matplotlib.axis.XTick at 0x7f179fbfc4e0>, <matplotlib.axis.XTick at 0x7f179facb320>, <matplotlib.axis.XTick at 0x7f179facb208>, <matplotlib.axis.XTick at 0x7f179fae84e0>], <a list of 4 Text xticklabel objects>)
matplotlib_spines_und_ticks 4: Graph 3

Gehen wir nochmal zurück zum vorigen Beispiel der Trigonometrischen Funktionen. Die meisten werden eine Beschriftung der X-Achse in Teilen bzw. Vielfachen von pi bevorzugen:

In [16]:
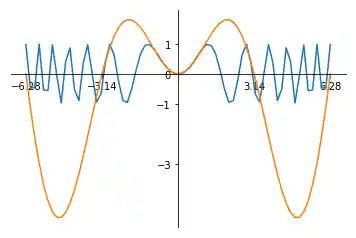
import numpy as np import matplotlib.pyplot as plt X = np.linspace(-2 * np.pi, 2 * np.pi, 70, endpoint=True) X = np.linspace(-2 * np.pi, 2 * np.pi, 70, endpoint=True) F1 = np.sin(X**2) F2 = X * np.sin(X) # aktuelle Achsen werden zurückgeliefert, # falls notwendig, werden sie erzeugt: ax = plt.gca() # der obere rechte Spine wird unsichtbar gemacht: ax.spines['top'].set_color('none') ax.spines['right'].set_color('none') # der untere Spine wird in Position y=0 gebracht: ax.xaxis.set_ticks_position('bottom') ax.spines['bottom'].set_position(('data',0)) # der linke Spine wird nach rechts zu x == 0 bewegt: ax.yaxis.set_ticks_position('left') ax.spines['left'].set_position(('data',0)) plt.xticks( [-6.28, -3.14, 3.14, 6.28]) plt.yticks([-3, -1, 0, +1, 3]) plt.plot(X, F1) plt.plot(X, F2) plt.show()
matplotlib_spines_und_ticks 5: Graph 4


Verändern der Achsenbeschriftungen

Wir möchten nun die Beschriftungen der X-Achse umbenennen und durch eigene Markierungen ersetzen. Wir benutzen dafür ebenfalls die Methode xticks wie auch schon im vorigen Beispiel. Diesmal jedoch, rufen wir xticks mit zwei Parametern auf: Der erste ist die gleiche Liste, die wir auch schon vorher benutzt haben, d.h. Positionen auf der X-Achse, an denen die Ticks gesetzt werden sollen. Der zweite Parameter ist eine Liste mit gleicher Anzahl von Elementen mit den entsprechenden LaTeX-Tick-Markierungen, d.h. der Text, der anstelle der Werte stehen soll. Die LaTeX-Schreibweise muss ein raw-String sein, um den Escape-Mechanismus von Python abzustellen, da in LaTeX das Backslash häufig genutzt wird.

In [17]:
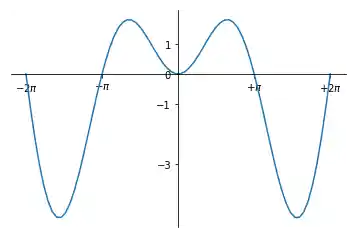
import numpy as np import matplotlib.pyplot as plt X = np.linspace(-2 * np.pi, 2 * np.pi, 70, endpoint=True) F1 = X * np.sin(X) ax = plt.gca() ax.spines['top'].set_color('none') ax.spines['right'].set_color('none') ax.xaxis.set_ticks_position('bottom') ax.spines['bottom'].set_position(('data',0)) ax.yaxis.set_ticks_position('left') ax.spines['left'].set_position(('data',0)) # Labelung der X-Achse: plt.xticks( [-6.28, -3.14, 3.14, 6.28], [r'$-2\pi$', r'$-\pi$', r'$+\pi$', r'$+2\pi$']) plt.yticks([-3, -1, 0, +1, 3]) plt.plot(X, F1) plt.show()
matplotlib_spines_und_ticks 6: Graph 5


Justierung der Tick-Beschriftungen

Wir wollen die Lesbarkeit der Tick-Beschriftungen erhöhen. Dazu vergrößern wir die Schrift und zeichnen diese auf einen halbtransparenten Hintergrund.

In [18]:
print(ax.get_xticklabels()) 
<a list of 4 Text xticklabel objects>
In [19]:
for xtick in ax.get_xticklabels(): print(xtick) 
Text(-6.28, 0, '$-2\\pi$') Text(-3.14, 0, '$-\\pi$') Text(3.14, 0, '$+\\pi$') Text(6.28, 0, '$+2\\pi$')

Jetzt vergrößern wir die Schrift und stellen die Transparenz ein:

In [20]:
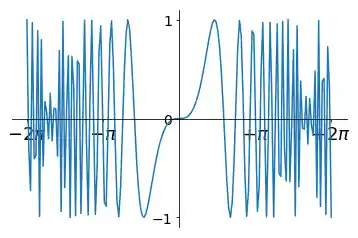
import numpy as np import matplotlib.pyplot as plt X = np.linspace(-2 * np.pi, 2 * np.pi, 170, endpoint=True) F1 = np.sin(X**3 / 2) ax = plt.gca() ax.spines['top'].set_color('none') ax.spines['right'].set_color('none') ax.xaxis.set_ticks_position('bottom') ax.spines['bottom'].set_position(('data',0)) ax.yaxis.set_ticks_position('left') ax.spines['left'].set_position(('data',0)) plt.xticks( [-6.28, -3.14, 3.14, 6.28], [r'$-2\pi$', r'$-\pi$', r'$+\pi$', r'$+2\pi$']) plt.yticks([-3, -1, 0, +1, 3]) for xtick in ax.get_xticklabels(): xtick.set_fontsize(18) xtick.set_bbox(dict(facecolor='white', edgecolor='None', alpha=0.7 )) for ytick in ax.get_yticklabels(): ytick.set_fontsize(14) ytick.set_bbox(dict(facecolor='white', edgecolor='None', alpha=0.7 )) plt.plot(X, F1, label="$sin(x)$")
Out[20]:
[<matplotlib.lines.Line2D at 0x7f179fa81518>]
matplotlib_spines_und_ticks 7: Graph 6
box

Numerisches Python

Die Bücher zur Webseite

Bücher zur Webseite

Im Hanser-Verlag sind vier Bücher von Bernd Klein und Philip Klein erschienen, die auf den Inhalten dieser Webseite aufbauen, aber auch über die Inhalte hinausgehen. Es lohnt sich also die Bücher zu kaufen, womit Sie außerdem diese Webseite unterstützen!

Einführung in Python3

Einführung in Python von Bernd Klein
Zum Online-Shop des Hanser-Verlages, wo Sie das Buch versandkostenfrei bestellen können!

Numerisches Python: Arbeiten mit NumPy, Matplotlib und Pandas

Bernd Klein: Python-Buch Numerisches Python Buch kaufen

Bernd Klein, Philip Klein:
Funktionale Programmierung mit Python

Bernd Klein, Philip Klein: Funktionale Programmierung mit Python Buch kaufen Python-Grundlagen | eLearning
Mit dem Hanser eCampus „Python-Grundlagen“ erhalten Einsteiger:innen eine Einführung in die Programmiersprache Python.

Python Grundlagen: elearning, Bernd Klein Buch kaufen



Bücher kaufen

Wenn Ihnen diese Webseite gefällt, - was wir natürlich sehr hoffen, - dann können Sie meine Arbeit unterstützen, wenn Sie eines meiner Bücher oder beide Bücher kaufen oder weiterempfehlen.

Die Bücher können Sie über jede Buchhandlung in Ihrer Nähe beziehen. Alternativ können Sie sie auch direkt über den Hanser-Verlag beziehen:
Bücher von Bernd Klein und Philip Klein

Spenden

Ihre Unterstützung ist dringend benötigt. Diese Webseite ist frei von Werbeblöcken und -bannern! So soll es auch bleiben! Dazu benötigen wir Ihre Unterstützung:

Weshalb wir Ihre Spende dringend benötigen erfahren Sie hier

Tutorial

Diese Webseite bietet ein Tutorial für Python. Der Unterschied zu anderen Online-Tutorials und Python-Kursen besteht darin, dass wir hier mehr Beispiele und Übungen bieten wollen. Außerdem werden komplexe Probleme in zahlreichen Diagrammen und Bildern veranschaulicht, um einen leichteren Zugang zu gewährleisten. In zahlreichen Python-Kursen hat Bernd Klein die Erfahrungen gesammelt, die in die Entwicklung dieser Webseite eingeflossen sind.

Fortgeschrittene Themen

Auf dieser Webseite befinden sich auch zahlreiche fortgeschrittene Themen zu Python, wie man sie in dieser Art vergeblich in anderen Python-Tutorials sucht. Themen, die insbesondere auch für Studierende der Informatik von besonderem Interesse sind: Turingmaschine, Endliche Automaten, Threads, Graphentheorie

Aber auch für Mathematikerinnen und Mathematiker, Ingenieurinnen und Ingenieure und andere naturwissenschaftlich Orientierte sind zum Beispiel die Einführungen in NumPy, Matplotlib und Pandas von großem Nutzen.


 


Suchen in dieser Webseite:

Webseite durchsuchen:

English Version / Englische Übersetzung

This chapter is also available in our English Python tutorial:

Schulungen

Wenn Sie Python schnell und effizient lernen wollen, empfehlen wir den Kurs Bodenseo, Linux, Python und viele andere Kurse
Einführung in Python von Bodenseo. Dieser Kurs wendet sich an totale Anfänger, was Programmierung betrifft. Wenn Sie bereits Erfahrung mit Python oder anderen Programmiersprachen haben, könnte der Python-Kurs für Fortgeschrittene der geeignete Kurs sein.

Python Courses


For those who prefer Python training courses in English: All our Python classes are available in English as well: Python Courses



Dem Autor Bernd Klein auf Facebook folgen:


Bernd Klein on Facebook

Spenden

Ihre Unterstützung ist dringend benötigt. Diese Webseite ist frei von Werbeblöcken und -bannern! So soll es auch bleiben! Dazu benötigen wir Ihre Unterstützung:

Weshalb wir Ihre Spende benötigen erfahren Sie hier

Spruch des Tages:

Wenn man sich fragt, ob Computer denken können, dann ist das, als ob man sich fragte, ob U-Boote schwimmen können. (frei nach Dijkstra)

Und noch ein Spruch:

Wenn man mit einer Schwierigkeit oder einer Kontroverse in der Wissenschaft  konfrontiert wird, ist ein Gramm Algebra so viel Wert wie eine Tonne sprachlicher Argumente.
 John Burdon Sanderson Haldane (1892-1964)

Hilfe

Diese Dokumentation zu Python mit Einführung und Tutorial wurde mit großer Sorgfalt erstellt und wird ständig erweitert. Dennoch können wir für die Korrektheit der Texte und der zahlreichen Beispiele keine Garantie übernehmen. Die Benutzung und Anwendung der Beispiele erfolgt auf eigenes Risiko. Wir freuen uns über alle Anregungen und Fehlerkorrekturen!



Datenschutzerklärung

Datenschutzerklärung nach DSGVO