Нейросети в трейдинге: Модели многократного уточнения прогнозов (Основные компоненты)
Введение
Современный финансовый рынок — это не просто набор котировок и индексов. Это сложная, динамическая система, где каждое изменение цены — отражение целой сети причин, взаимодействий и ожиданий. Поток данных, поступающих ежесекундно, напоминает живое движение, в котором каждое мгновение несёт смысл. Увидеть это движение — значит научиться читать рынок как процесс, а не результат. Именно к этому стремится фреймворк RAFT — Recurrent All-Pairs Field Transforms, чья архитектура изначально была создана для понимания динамики в последовательностях изображений, но идеально ложится и на природу рыночных временных рядов.
Основная концепция фреймворка RAFT — способность мыслить в категориях движения, непрерывности и уточнения.
В классическом трейдинге цена рассматривается как ряд дискретных значений — свечей, баров, тиков. Аналитик видит последовательность и пытается выделить закономерность. Однако реальный рынок течёт, как река. Он не прыгает из точки в точку, а переливается из состояния в состояние, меняя направление и скорость под действием тысячи различных факторов. И вот здесь философия RAFT проявляется особенно чётко. Модель воспринимает данные не как набор снимков, а как поток. Каждое новое состояние связано с предыдущим множеством скрытых зависимостей. В терминах компьютерного зрения — это оценка оптического потока. Здесь важно не то, что видно в кадре, а то, как и куда всё движется между ними. В терминах финансов — это не просто прогноз следующей цены, а понимание направленности и силы движения рынка.
В основе RAFT лежит идея постоянного уточнения прогноза. Модель не делает окончательный вывод сразу, а возвращается к нему много раз, каждый раз сверяя новую информацию с уже полученными результатами. Этот рекуррентный характер напоминает работу опытного аналитика, который корректирует свои предположения при поступлении новых данных, сохраняя общий контекст. Благодаря этому RAFT достигает высокой устойчивости даже на фоне сильных рыночных колебаний, когда традиционные алгоритмы теряют синхронизацию с потоком событий. В финансовом анализе это качество особенно важно, ведь рынок редко бывает предсказуем. Импульсы сменяются откатами, а устойчивые тренды порой рушатся за считанные минуты. Способность модели пересматривать свои решения делает её ближе к реальному мышлению — гибкому, итеративному и способному к самоадаптации.
Если рассматривать внутреннюю структуру RAFT с методологической точки зрения, то она строится на трёх взаимосвязанных идеях:
- извлечении признаков,
- формировании связей между ними,
- итеративном уточнении этих связей.
Признаки описывают состояние системы. В нашем случае, это характеристики рынка: волатильность, импульс, баланс спроса и предложения, корреляции между активами. Далее формируется поле всех возможных взаимодействий, своего рода рыночная карта связей, в которой каждая точка отражает взаимное влияние состояний системы во времени. И наконец, рекуррентный блок шаг за шагом уточняет это поле, приближая модель к наиболее достоверному представлению рыночного движения. Таким образом, RAFT не просто ищет ответ, а «ведёт диалог» с данными, уточняя свои суждения на каждом шаге.
На первый взгляд может показаться, что между компьютерным зрением и финансовыми данными нет ничего общего. Но если заменить кадры на временные окна, а пиксели на признаки активов, становится очевидно, насколько близки эти два мира. И там и здесь мы имеем дело с потоком информации, где каждое изменение несёт смысл только в контексте предыдущих. Каждый новый тик — это не изолированное событие, а продолжение рыночной истории, вписанное в общую ткань движения. RAFT как раз и создаёт этот контекст, строя поле смещений — нечто вроде карты движения ликвидности, где можно видеть направления и интенсивность изменений. Это открывает возможности не только прогнозирования, но и интерпретации. Исследователь получает инструмент для визуализации динамики рынка, способный наблюдать, где ускоряются тренды, где зарождаются развороты, а где силы рынка приходят в равновесие.
В отличие от тяжеловесных нейросетевых систем, RAFT сочетает вычислительную эффективность с концептуальной глубиной. Его структура лаконична, а процесс итеративного уточнения не требует гигантских ресурсов. Это особенно ценно для реализации в среде MQL5, где эффективность кода и скорость обработки данных — первоочередные требования. Модель можно адаптировать под реальные рыночные условия без ущерба для точности и стабильности. Более того, её рекуррентная природа делает возможным живой отклик на поток тиков, а не только анализ исторических выборок.
Но пожалуй, главное достоинство RAFT — это интеллектуальная гибкость. Он не застывает в пределах одного паттерна и не полагается на единожды выученную схему. Каждый новый срез данных становится для модели поводом пересмотреть собственные выводы. В этом проявляется её философия — не предсказывать рынок как статичный объект, а адаптироваться к его движению, мыслить вместе с ним. В условиях постоянной изменчивости такая способность ценнее любой точности: ведь рынок редко бывает правильным, но всегда остаётся живым.
В своей работе мы сосредоточим внимание на архитектуре и структуре фреймворка RAFT. Разберём принципы его работы и подготовим основу для пошаговой реализации средствами MQL5. Цель проста и амбициозна — показать, как эта модель, созданная для анализа движения в видеопотоках, может стать мощным инструментом в анализе движения финансовых данных. Ведь если научиться видеть в этом потоке структуру, можно приблизиться к тому, что всегда было мечтой трейдера — понять куда движется цена, и почему она движется именно туда.
Авторская визуализация фреймворка RAFT представлена ниже.
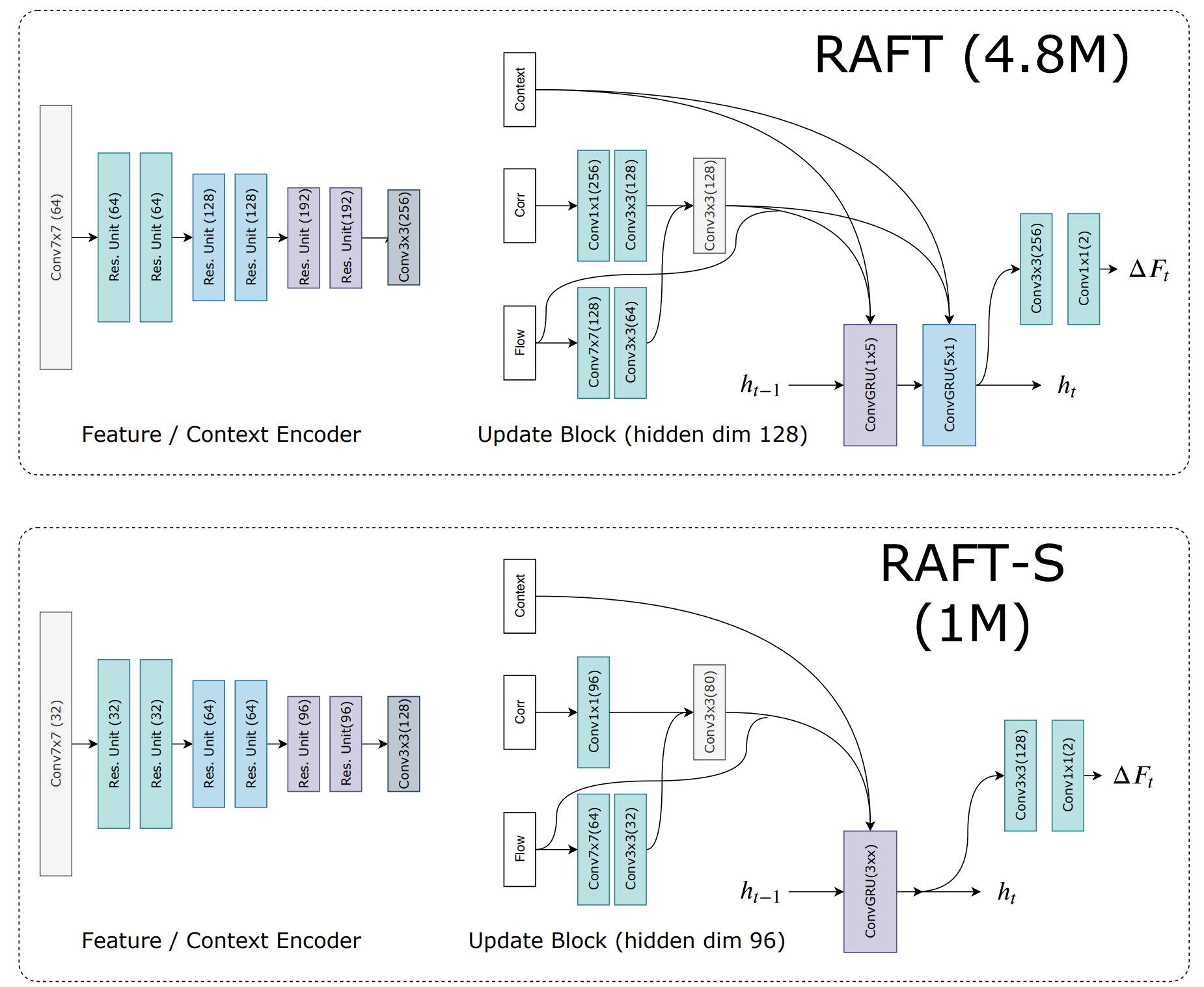
Модуль мультимасштабной корреляции
Чтобы фреймвокр RAFT заговорил языком рынков, мы начинаем с построения карты корреляции признаков. В качестве основы логично использовать уже созданные наработки, созданные в рамках работы над STE-FlowNet. Как и ранее, вместо фиксированного начального состояния, предложенного авторами фреймворка, мы используем стек последних состояний системы. Такой подход позволяет модели видеть не просто текущее значение индикатора, а контекст его движения: динамику, ускорение, инерцию. Это как если бы трейдер оценивал не одну свечу, а целую историю колебаний цены, выстраивая причинно-следственную логику её поведения.
Однако классическая карта корреляций RAFT опирается на координатное пространство, где перемещения объектов имеют направление и масштаб. В финансовых данных координатной сетки нет. Импульсы не перемещаются по признакам, а развиваются во времени. Поэтому масштабирование в нашем случае переносится на временную ось. Мы создаём аналог пирамиды корреляций, но по шкале времени. Каждый уровень отражает определённую глубину истории — от краткосрочных колебаний до фундаментальных трендов. Это даёт возможность RAFT видеть рынок в нескольких временных измерениях, улавливая микроколебания и длительные волновые структуры, формируя более устойчивое и адаптивное восприятие данных.
Затем организуем построение многомасштабной карты признаков. Сначала она создаётся для каждого временного диапазона, фиксируя быстрые и медленные изменения. Все эти уровни объединяются в общий тензор, который поступает в стек состояний. Такая иерархия даёт модели способность одновременно учитывать мгновенные реакции рынка и его инерционные сдвиги — то, что в классических методах часто теряется.
В практической части предыдущей статьи мы реализовали OpenCL-кернел, выполняющий агрегацию и усреднение признаков для всех уровней временной пирамиды. Этот шаг позволил формировать согласованные представления данных на разных масштабах, создавая прочный фундамент для последующих вычислений. Сегодня мы движемся дальше и переходим к созданию специализированного объекта мультимасштабной корреляции признаков на стороне основной программы. Он станет ядром нашей реализации RAFT-механизма в финансовом контексте, своеобразным зрением системы, способным распознавать взаимосвязи между состояниями рынка с разной глубиной истории.
class CNeuronMultiScaleStackCorrelation : public CNeuronStackCorrelation { protected: uint iLevels; CNeuronBaseOCL cScales; //--- virtual bool AggregationByTime(CNeuronBaseOCL *NeuronOCL); virtual bool AggregationByTimeGrad(CNeuronBaseOCL *NeuronOCL); //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override; public: CNeuronMultiScaleStackCorrelation(void) {}; ~CNeuronMultiScaleStackCorrelation(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint stack_size, uint dimension, uint variables, uint levels, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) override const { return defNeuronMultiScaleStackCorrelation; } //--- methods for working with files virtual bool Save(int const file_handle) override; virtual bool Load(int const file_handle) override; //--- virtual void SetOpenCL(COpenCLMy *obj) override; //--- virtual uint GetLevels(void) const { return iLevels; } virtual uint GetVariables(void) override const { return GetVariables() / iLevels; } };
Новый объект наследует базовую функциональность класса CNeuronStackCorrelation и расширяет механизм корреляции состояний, добавляя поддержку многомасштабного анализа — способности рассматривать данные сразу на нескольких уровнях временной глубины. В контексте финансовых временных рядов это эквивалентно наблюдению за движением цены не только в краткосрочной перспективе, но и на старших таймфреймах.
В представленной структуре добавляется переменная iLevels, определяющая количество масштабов временной пирамиды. Иными словами, сколько уровней анализа система будет использовать. Каждый уровень соответствует определённому временному окну.
Объект cScales представляет собой экземпляр базового класса CNeuronBaseOCL и предназначен для временного хранения пирамиды признаков анализируемого состояния.
Метод Init играет роль своеобразного архитектора — он не просто подготавливает объект к работе, а выстраивает целую инфраструктуру многомасштабного восприятия данных. Именно здесь происходит соединение математической логики с вычислительной архитектурой, превращая абстрактную идею временной пирамиды в реальный рабочий механизм.
bool CNeuronMultiScaleStackCorrelation::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint stack_size, uint dimension, uint variables, uint levels, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronStackCorrelation::Init(numOutputs, myIndex, open_cl, stack_size, dimension, variables * levels, optimization_type, batch)) return false;
С момента вызова метода начинается пошаговая инициализация структуры, которая объединяет разные временные масштабы анализа в единую систему. На вход подаются основные параметры конфигурации — количество выходов, индекс текущего нейрона, ссылка на объект управления OpenCL, глубина временного стека, размерность данных, число признаков, количество масштабов, тип оптимизации и размер пакета данных. Все эти параметры вместе определяют, как именно нейрон будет воспринимать временной контекст, насколько глубоко сможет «заглядывать» в прошлое и с какой детализацией анализировать рынок.
Первым шагом вызывается одноименный метод родительского класса. Этот вызов можно рассматривать как закладку фундамента. Он формирует основную структуру корреляционного стека, выделяет память и подготавливает OpenCL-буферы. Но здесь есть одно принципиальное отличие — количество признаков умножается на число уровней временной пирамиды. Такой приём создаёт объединённое признаковое пространство, где каждый уровень получает свой набор данных, отражающий рынок с разной глубиной временной перспективы. Если базовая инициализация по какой-либо причине завершается неудачно, метод немедленно прерывает выполнение, чтобы избежать непредсказуемых ошибок.
После успешного завершения базовой инициализации, в переменной iLevels фиксируется число уровней временной пирамиды. Это значение становится внутренним ориентиром для всех последующих вычислений и определяет, сколько временных масштабов будет участвовать в построении корреляционной структуры.
iLevels = levels; if(!cScales.Init(0, 0, OpenCL, dimension * levels * variables, optimization, iBatch)) return false; //--- return true; }
Следующим шагом инициализируется объект cScales, отвечающий за хранение масштабных признаков. По сути, в этом месте формируется цифровой аналог многослойного восприятия: система начинает видеть рынок одновременно на нескольких временных горизонтах — от краткосрочных колебаний до долгосрочных тенденций.
Если создание контейнера cScales проходит успешно, метод завершает инициализацию и возвращает true. Это короткое, но важное завершение символизирует готовность объекта к работе. С этого момента CNeuronMultiScaleStackCorrelation становится полноценным узлом вычислительного графа, способным аккумулировать, масштабировать и интерпретировать динамику финансовых данных во времени.
Всё происходящее внутри этого метода можно представить как процесс настройки сложного аналитического инструмента, где каждый параметр имеет свой смысл и назначение.
Алгоритм прямого прохода в классе CNeuronMultiScaleStackCorrelation реализует ключевую логику многомасштабной корреляционной обработки данных — именно здесь происходит объединение временной агрегации, масштабного анализа и матричных преобразований, формирующих итоговый отклик нейронного блока.
bool CNeuronMultiScaleStackCorrelation::feedForward(CNeuronBaseOCL *NeuronOCL) { if(!AggregationByTime(NeuronOCL)) return false;
Работа метода начинается с обращения к методу AggregationByTime, который представляет собой обёртку для одноимённого OpenCL-кернела, реализованного нами в практической части прошлой статьи. На этом этапе происходит агрегирование текущих признаков вместе с информацией о предыдущих состояниях из стека, выстраивая их в логически согласованную структуру по временной оси. Этот шаг позволяет выявлять устойчивые динамические зависимости и одновременно сглаживать случайные колебания, характерные для финансовых временных рядов.
Следующий этап — добавление полученной информации в стек накопления истории состояний.
if(!cStack.FeedForward(cScales.AsObject())) return false;
Когда все масштабные компоненты вычислены, метод переходит к матричному умножению стеку накопленной истории к детальному представлению анализируемого состояния. Здесь происходит объединение масштабных признаков в итоговый вектор отклика.
if(!MatMul(cStack.getOutput(), NeuronOCL.getOutput(), Output, GetStackSize() * GetLevels(), GetDimension(), 1, GetVariables(), true)) return false;
Обратите внимание, параметры функции чётко задают размеры матриц. Выполняется произведение матрицами размерностью [(StackSize × Levels), Dimension] на вектор столбец [Dimension]. При этом осуществляется параллельное вычисление Variables независимых произведений, формируя матрицы корреляций каждой унитарной последовательности на заданном горизонте в указанном количестве масштабов. По сути, этот этап выполняет синтез информации, аккумулируя все уровни корреляций и масштабов в единый, обобщённый результат, готовый к дальнейшей обработке.
Завершающим этапом становится применение функции активации. Конечно, если таковая задана пользователем.
if(activation != None) if(!Activation(Output, Output, activation)) return false; //--- return true; }
Алгоритм метода выстроен логично и прозрачно: от временной агрегации — к многомасштабному анализу, далее к синтезу и нелинейному отклику. Такая архитектура позволяет эффективно извлекать скрытые зависимости из динамичных, многомерных данных, сохраняя при этом структурную устойчивость и интерпретируемость результата.
Как вы могли заметить, данный модуль не содержит обучаемых параметров, однако он играет важную роль как один из компонентов нашей нейронной модели. И как известно, сама модель требует обучения. Чтобы наш модуль мультимасштабной корреляции не стал препятствием в процессе обучения, необходимо обеспечить корректное распространение градиентов ошибки до всех участников вычислительного графа в соответствии с их вкладом в итоговый результат. Этот механизм реализован в методе calcInputGradients.
bool CNeuronMultiScaleStackCorrelation::calcInputGradients(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL) return false;
Работа метода начинается с проверки корректности полученного указателя на объект исходных данных, что позволяет избежать некорректных вызовов.
Основное вычисление градиентов начинается с вызова функции MatMulGrad, которая выполняет обратное матричное умножение для распространения градиентов ошибок от выходных матриц корреляций к исходным данным и стеку масштабных признаков.
if(!MatMulGrad(cStack.getOutput(), cStack.getGradient(), NeuronOCL.getOutput(), cScales.getGradient(), Gradient, GetStackSize()*GetLevels(), GetDimension(), 1, GetVariables(), true)) return false;
Здесь учитываются все уровни временной пирамиды и каждый признак, а параллельное вычисление обеспечивает эффективность обработки больших временных рядов.
Далее вызывается AggregationByTimeGrad, выполняющий обратное распространение градиентов через временную агрегацию. Этот шаг гарантирует, что вклад каждого временного состояния корректно учитывается при корректировке параметров модели.
if(!AggregationByTimeGrad(NeuronOCL)) return false;
Здесь важно отметить, что параметры анализируемого состояния участвуют одновременно в двух процессах: при матричном умножении, для вычисления корреляций, и при агрегации мультимасштабных признаков. Поэтому возникает необходимость аккуратно объединить градиенты, полученные из этих двух информационных потоков. Функция SumAndNormilize как раз выполняет эту задачу. Она суммирует значения, обеспечивая баланс и согласованность градиентов. Благодаря этому модель корректно обновляет свои обучаемые компоненты, не допуская переоценки влияния одних уровней по сравнению с другими.
if(!SumAndNormilize(NeuronOCL.getGradient(), cScales.getGradient(), NeuronOCL.getGradient(), GetDimension(), false, 0, 0, 0, 1)) return false; Deactivation(NeuronOCL) //--- return true; }
Завершает процесс вызов Deactivation, который корректирует градиенты на производную функции активации, приводя их в форму, пригодную для дальнейшего распространения.
В итоге, метод calcInputGradients превращает модуль мультимасштабной корреляции из пассивного блока в активного участника процесса обучения, аккуратно распределяя ошибку между всеми связанными компонентами и обеспечивая стабильное и корректное обучение всей нейронной модели.
Блок 2D-GRU
После того как мы собрали модуль мультимасштабной корреляции, логично повернуть внимание к следующему критичному звену — сверточным GRU. Авторы фреймворка RAFT предлагают не одну, а две последовательные сверточные GRU-единицы. Причём каждая из них работает в своём измерении координатной плоскости. В терминах визуальной задачи это означает, что первая группа свёрток может учитывать горизонтальные зависимости, вторая — вертикальные, и их последовательное действие даёт более глубокое представление о локальных и глобальных смещениях. В финансовом контексте аналогичная идея переводится на работу по разным осям. Одна GRU-ветвь может выстраивать временную динамику внутри одного набора признаков, вторая — фиксировать взаимодействия между наборами признаков. Ключевое требование здесь — не просто последовательное подключение двух уже имеющихся модулей, а организация единого потока данных, где скрытые состояния и исходные данные используются совместно и синхронно.
Если попытаться склеить две стандартные реализации подряд, мы столкнёмся с ограничением. Каждая из них будет работать в своём собственном пространстве состояний и не сможет эффективно разделять скрытое состояние с соседней ветвью, а также одновременно обращаться к тем же исходным данным корреляции. Нам нужен модуль, который внутри себя реализует две стадии сверточного GRU, но рассматривается в архитектуре как единый узел — с общими интерфейсами, единым управлением памятью и предсказуемым протоколом передачи скрытых состояний. Такой модуль должен принимать на вход агрегированные корреляционные карты и признаки, иметь внутренние буферы для скрытых состояний двух стадий и уметь обеспечивать параллельный доступ обеих стадий к исходным тензорам без избыточного копирования.
Предложенную авторами фреймворка RAFT идею двухмерной обработки данных мы реализуем в классе CNeuronSpikeConvGRU2D — расширенной версии сверточного GRU, специально адаптированной под анализ сигналов в двух направлениях. Этот модуль наследует базовый функционал от CNeuronSpikeConvGRU, но дополняет его вторым уровнем вычислений. Это позволяет одновременно учитывать временные зависимости и взаимосвязи между признаками. Такая структура создаёт более глубокое восприятие данных, где каждый шаг модели опирается не только на предыдущее состояние, но и на пространственный контекст, повышая точность итеративного уточнения прогноза.
class CNeuronSpikeConvGRU2D : public CNeuronSpikeConvGRU { protected: CNeuronConvOCL cProjectionX; CNeuronBaseOCL cConcatenated2[2]; CNeuronConvOCL cZR2; CNeuronBaseOCL cZ2; CNeuronBaseOCL cR2; CNeuronConvOCL cHt2; CNeuronBaseOCL cH2; CNeuronTransposeOCL cTranspose[3]; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override; public: CNeuronSpikeConvGRU2D(void) {}; ~CNeuronSpikeConvGRU2D(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint units, uint chanels_in, uint chanels_out, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) override const { return defNeuronSpikeConvGRU2D; } //--- methods for working with files virtual bool Save(int const file_handle) override; virtual bool Load(int const file_handle) override; //--- virtual void SetOpenCL(COpenCLMy *obj) override; //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau) override; //--- virtual uint GetChanels(void) const { return cHt.GetFilters(); } virtual uint GetUnits(void) const { return cHt.GetUnits(); } };
В защищённой области класса размещены основные вычислительные узлы. Компонент cProjectionX выполняет проекцию входных признаков в альтернативное пространство, формируя независимое представление для второй итерации GRU и согласуя размерность признаков исходных данных с анализируемым измерением скрытого состояния. По сути, он создаёт дополнительный взгляд на данные, обеспечивая перекрёстную чувствительность между временными и корреляционными связями. Это особенно важно в задачах финансового анализа, где поведение одного актива может оказывать влияние на целую группу связанных инструментов.
Далее идут два буфера cConcatenated2[2], служащие для объединения выходов первой стадии с исходными данными. Такой приём создаёт обогащённый контекст, где в одном тензоре собраны и новые и исходные признаки. Благодаря этому, вторая GRU-ячейка получает полное представление о состоянии системы — как о текущем изменении, так и о его первопричине. Это напоминает процесс пересмотра прогноза: сначала модель делает предварительное предположение, затем, учитывая контекст и уточнённые данные, корректирует своё решение.
Блоки cZR2, cZ2, cR2, cHt2 и cH2 составляют внутреннюю структуру второй стадии GRU. В совокупности они создают замкнутый механизм двойного обновления, при котором информация уточняется постепенно, но непрерывно.
Три объекта cTranspose[3] обеспечивают переориентацию данных между стадиями. В финансовой трактовке это позволяет чередовать временное и факторное измерение: рассматривать одни и те же признаки как динамику по времени или как взаимосвязи между активами. Это добавляет модели многомерное восприятие рынка, делая анализ не линейным, а пространственным.
Процесс инициализации внутренних компонентов модуля — это тщательно продуманный этап, в котором каждый элемент получает своё место и функциональную роль в общей схеме. Всё начинается с вызова одноименного метода родительского класса, который подготавливает основу архитектуры, наследуя ключевые свойства классического сверточного GRU.
bool CNeuronSpikeConvGRU2D::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint units, uint chanels_in, uint chanels_out, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronSpikeConvGRU::Init(numOutputs, myIndex, open_cl, units, chanels_in, chanels_out, optimization_type, batch)) return false;
Этот шаг не просто формальность: он обеспечивает корректную настройку вычислительного окружения OpenCL, связывает объект с контекстом обработки и формирует базовые структуры данных, на которых строится вся дальнейшая логика.
После успешной инициализации базового уровня, активируется блок cProjectionX, выполняющий роль проекционного преобразователя. Его задача — адаптировать входные тензоры к внутренним размерностям модели, то есть привести число каналов и размер фильтров к единому стандарту. По сути, этот слой выступает в роли входного моста, который сглаживает различия между масштабами данных и подготавливает их к глубинной обработке. Активационная функция для него намеренно отключена — на этом этапе требуется сохранить исходную структуру признаков без дополнительного искажения.
uint index = 0; if(!cProjectionX.Init(0, index, OpenCL, chanels_in, chanels_in, chanels_out, units, optimization, iBatch)) return false; cProjectionX.SetActivationFunction(None);
Далее инициализируются два объекта cConcatenated2, каждый из которых отвечает за объединение данных из разных источников. Отсутствие активации и здесь не случайно — объединение должно быть линейным, чтобы не нарушить баланс сигналов между ветвями модели.
index++; for(uint i = 0; i < cConcatenated2.Size(); i++) { if(!cConcatenated2[i].Init(0, index, OpenCL, 2 * units * chanels_in, optimization, iBatch)) return false; cConcatenated[i].SetActivationFunction(None); index++; }
Следующим шагом формируются транспонирующие блоки cTranspose. Их три, и каждый выполняет строго определённую функцию: первый — проецирует данные скрытого состояния предыдущего шага, второй — обеспечивает аналогичную проекцию исходных данных, третий — восстанавливает исходную структуру при передаче нового скрытого состояния на следующий уровень. Эти операции можно сравнить с переворачиванием шахматной доски — ориентация данных меняется, но их логические связи сохраняются. Такой приём позволяет работать с информацией одновременно в двух измерениях, что и является ключевой особенностью подхода RAFT.
if(!cTranspose[0].Init(0, index, OpenCL, units, chanels_out, optimization, iBatch)) return false; index++; if(!cTranspose[1].Init(0, index, OpenCL, units, chanels_out, optimization, iBatch)) return false; index++; if(!cTranspose[2].Init(0, index, OpenCL, chanels_out, units, optimization, iBatch)) return false;
Далее начинается построение второго уровня GRU, представленного объектами cZR2, cZ2, cR2 и cHt2. Компонент cZR2 формирует вектор управляющих врат — обновления и сброса, которые регулируют, какая часть прошлой информации должна быть сохранена, а какая заменена новыми данными. Его сигмоидальная активация делает процесс решения модели плавным и дифференцируемым, что особенно важно для корректного обучения.
index++; if(!cZR2.Init(0, index, OpenCL, 2 * units, 2 * units, 2 * units, chanels_out, 1, optimization, iBatch)) return false; cZR2.SetActivationFunction(SIGMOID);
Блоки cZ2 и cR2 отделяют управляющие сигналы и подготавливают их для следующего этапа — вычисления кандидатов нового состояния в cHt2. Здесь используется функция активации TANH, задающая сбалансированный диапазон значений и обеспечивающая стабильность при обучении даже на длинных временных сериях.
index++; if(!cZ2.Init(0, index, OpenCL, cZR2.Neurons() / 2, optimization, iBatch)) return false; cZ2.SetActivationFunction((ENUM_ACTIVATION)cZR2.Activation()); index++; if(!cR2.Init(0, index, OpenCL, cZR2.Neurons() / 2, optimization, iBatch)) return false; cR2.SetActivationFunction((ENUM_ACTIVATION)cZR2.Activation()); index++; if(!cHt2.Init(0, index, OpenCL, 2 * units, 2 * units, units, chanels_out, 1, optimization, iBatch)) return false; cHt2.SetActivationFunction(TANH);
Вся эта цепочка напоминает точный хронометр, где каждая шестерёнка отвечает за свой участок движения, но все вместе они создают слаженный ритм.
Финальный элемент инициализации — cH2, аккумулирующий результаты обработки данных. Этот блок собирает в единое целое все промежуточные вычисления, создавая целостное представление текущего состояния системы. На этом этапе модель готова принимать поток данных и выполнять многомерный анализ, выявляя взаимосвязи, недоступные классическим одномерным архитектурам.
index++; if(!cH2.Init(0, index, OpenCL, units * chanels_out, optimization, iBatch)) return false; //--- return true; }
Таким образом, метод Init выстраивает целую вычислительную экосистему, где каждый компонент точно знает своё место и взаимодействует с другими по принципу согласованного обмена информацией.
Алгоритм прямого прохода, организованный в методе feedForward, представляет собой тщательно выстроенную последовательность вычислений, в которой двухмерная рекуррентная логика соединяется с принципами сверточной обработки данных. Каждый шаг здесь не просто операция, а звено в цепи преобразований, направленных на извлечение и синтез глубинных взаимосвязей между пространственными и временными компонентами входного потока.
bool CNeuronSpikeConvGRU2D::feedForward(CNeuronBaseOCL *NeuronOCL) { if(!cProjectionX.FeedForward(NeuronOCL)) return false; if(!cTranspose[0].FeedForward(cH.AsObject())) return false; if(!cTranspose[1].FeedForward(cProjectionX.AsObject())) return false;
Работа алгоритма начинается с проекционного преобразования исходных данных через блок cProjectionX. Этот элемент выполняет роль адаптера между исходными признаками и внутренними представлениями модели, переводя данные в формат, пригодный для двухмерного анализа. Далее в дело вступают транспонирующие слои — cTranspose[0] и cTranspose[1], которые перестраивают тензоры вдоль координатных осей. Это позволяет объединить пространственные и временные измерения, создавая основу для перекрёстного взаимодействия данных по обоим направлениям.
После подготовки данных вычисляются ключевые параметры: количество временных шагов (units), число скрытых каналов (hidden) и размер входного окна (inputs). Эти параметры определяют архитектурную конфигурацию текущей итерации прямого прохода и обеспечивают согласованность всех дальнейших операций.
uint units = cHt.GetUnits(); uint hidden = cHt.GetFilters(); uint inputs = cHt.GetWindow() - hidden;
Затем выполняется первая стадия объединения потоков данных — операция Concat, которая формирует общий контекст для вычисления управляющих врат второго GRU-блока. Здесь объединяются выходы транспонированных слоёв.
if(!Concat(cTranspose[0].getOutput(), cTranspose[1].getOutput(), cConcatenated2[0].getOutput(), units, units, hidden)) return false;
Полученный тензор передаётся в блок cZR2, который отвечает за генерацию векторов обновления и сброса. Эти управляющие сигналы — своего рода нейронные рычаги, регулирующие, какая часть прошлой информации сохраняется, а какая заменяется новой.
if(!cZR2.FeedForward(cConcatenated2[0].AsObject())) return false; if(!DeConcat(cZ2.getOutput(), cR2.getOutput(), cZR2.getOutput(), units, units, hidden)) return false;
После этого данные разделяются на два потока: cZ2 и cR2, каждый из которых выполняет свою функцию в механизме адаптивного запоминания. Поток сброса (cR2) взаимодействует с выходом первого транспонированного слоя, корректируя степень влияния предыдущего состояния.
if(!ElementMult(cR2.getOutput(), cTranspose[0].getOutput(), cR2.getPrevOutput())) return false; if(!Concat(cR2.getPrevOutput(), cTranspose[1].getOutput(), cConcatenated2[1].getOutput(), units, units, hidden)) return false; if(!cHt2.FeedForward(cConcatenated2[1].AsObject())) return false;
Результаты вновь объединяются через вторую операцию Concat, формируя основу для вычисления нового кандидата состояния в блоке cHt2. На этом этапе происходит нелинейное преобразование с активацией TANH, формирующее обновлённое представление признаков.
Далее выполняется операция GateElementMult, где кандидатное состояние cHt2 смешивается с предыдущим состоянием под управлением ворот обновления cZ2. Это позволяет системе динамически регулировать баланс между памятью и обновлением, создавая устойчивое, но гибкое внутреннее представление.
if(!GateElementMult(cHt2.getOutput(), cTranspose[0].getOutput(), cZ2.getOutput(), cH2.getOutput())) return false; if(!cTranspose[2].FeedForward(cH2.AsObject())) return false;
Полученный результат преобразуется обратно с помощью cTranspose[2], возвращаясь в исходное измерение, где происходит вторая стадия GRU-процессинга — уже в классическом направлении, аналогичном стандартному сверточному GRU.
if(!Concat(NeuronOCL.getOutput(), cTranspose[2].getOutput(), cConcatenated[0].getOutput(), inputs, hidden, units)) return false; if(!cZR.FeedForward(cConcatenated[0].AsObject())) return false; if(!DeConcat(cZ.getOutput(), cR.getOutput(), cZR.getOutput(), hidden, hidden, units)) return false; if(!ElementMult(cR.getOutput(), cTranspose[2].getOutput(), cR.getPrevOutput())) return false; if(!Concat(NeuronOCL.getOutput(), cR.getPrevOutput(), cConcatenated[1].getOutput(), inputs, hidden, units)) return false; if(!cHt.FeedForward(cConcatenated[1].AsObject())) return false; if(!GateElementMult(cHt.getOutput(), cTranspose[2].getOutput(), cZ.getOutput(), cH.getOutput())) return false;
После этого выход проходит через нормализующий блок cNorm, где значения стабилизируются, устраняя накопленные отклонения, и подаётся на финальную стадию — активацию CNeuronSpikeActivation, придающую выходу модели нелинейный отклик, соответствующий нейронной динамике спайкового типа.
В результате весь алгоритм прямого прохода формирует скоординированный поток вычислений, в котором каждый уровень дополняет другой, обеспечивая модели способность видеть многомерные зависимости в данных. Это не просто последовательность операций, а своеобразный диалог между пространством и временем, где сигналы обмениваются информацией, уточняют и усиливают друг друга. Именно эта архитектурная гармония делает модуль CNeuronSpikeConvGRU2D ключевым звеном в реализации RAFT, обеспечивая глубинное восприятие структуры данных и высокую адаптивность при анализе сложных динамических процессов — от потоков изображений до финансовых временных рядов.
Сегодня мы проделали серьёзную и продуктивную работу — построили основные компоненты фреймворка RAFT, заложив фундамент его вычислительной архитектуры. Самое время сделать небольшую паузу и позволить мыслям улечься. Впереди нас ждёт заключительный этап — объединение всех созданных модулей в единую, скоординированную структуру. Именно этому мы посвятим следующую статью.
Заключение
В этой статье мы шаг за шагом приблизились к практической реализации ключевых идей фреймворка RAFT, адаптировав их под специфику финансового анализа. Мы создали модуль мультимасштабной корреляции признаков и реализовали двухмерный сверточный блок GRU, который позволяет учитывать как временные, так и структурные зависимости данных. Эти компоненты стали логическим продолжением предыдущих разработок и открыли путь к построению полноценной итеративной модели прогнозирования рыночной динамики. В следующей статье мы объединим все созданные элементы в единую систему, протестируем её в действии и оценим эффективность реализованных подходов на реальных исторических данных.
Ссылки
Программы, используемые в статье
| # | Имя | Тип | Описание |
|---|---|---|---|
| 1 | Study.mq5 | Советник | Советник офлайн обучения моделей |
| 2 | StudyOnline.mq5 | Советник | Советник онлайн обучения моделей |
| 3 | Test.mq5 | Советник | Советник для тестирования модели |
| 4 | Trajectory.mqh | Библиотека класса | Структура описания состояния системы и архитектуры моделей |
| 5 | NeuroNet.mqh | Библиотека класса | Библиотека классов для создания нейронной сети |
| 6 | NeuroNet.cl | Библиотека | Библиотека кода OpenCL-программы |