"""
**************************
De parvis grandis acervus erit
**************************
NumeroEuler.py
**************************
Hilario Iglesias Martínez.
**************************
Ecuacion para datos de entrada:
f(x,z)=(x**2/4)+(e*z)
e=Número de Eulen.
2.71828
Valores 5,12. La salida real debería ser=38.86936
Realizado bajo plataforma Linux.
Ubuntu 20.04.6 LTS.
Google Colaboratory.
"""
from keras.activations import relu
from keras.api._v2.keras import activations
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
#Matriz tipo 21,2
Valores_Entrada=np.array([[3,6],
[4,9],
[8,7],
[9,5],
[6,8],
[7,3],
[10,3],
[2.5,3.8],
[13,1.4],
[1.8,19],
[2.6,12],
[7.5,45],
[10.4,13],
[3.45,21],
[18.7,7],
[9,13],
[7.67,56],
[2.3,56],
[76,1.67],
[10.12,86.3],
[20,99]],dtype=float)
#Matriz tipo 21,1
Valores_Salida=np.array([[17.434],
[26.464],
[27.027],
[23.716],
[26.246],
[14.279],
[33.154],
[11.891],
[46.055],
[52.455],
[34.308],
[136.381],
[62.376],
[60.057],
[106.449],
[55.586],
[166.926],
[8.281],
[1448.539],
[260.191],
[369.109]],dtype=float)
"""
Vamos a crear el modelo neuronal. Como tenemos dos tipos de datos
deiferentes atributos de entrada, pondremos dos neuronas de entrada, que admitirá
6 tipos de datos diferente.
"""
#Modelo=tf.keras.Sequential([ŧf.keras.layers.Dense(units=12,activations='relu',Valores_Entrada[2])),
# tf.keras.layers.Dense(units=1)])
Modelo_Adoptado = tf.keras.Sequential([
tf.keras.layers.Dense(units=12, activation='relu', input_shape=(Valores_Entrada.shape[1],)),
tf.keras.layers.Dense(units=1)])
print('\n')print("MODELO ADOPTADO:")print(Modelo_Adoptado)
print("*************************************************************")print('\n')#Compilamos el modelo.
Modelo_Adoptado.compile(optimizer='Adam',loss='mean_squared_error')
#Entrenamos el modelo
Modelo_Adoptado.fit(Valores_Entrada,Valores_Salida,epochs=80000,verbose=0)
#Le vamos a mandar hacer una predicción para dos valores.
Nuevo_Valor_x=np.array([[5,12]],dtype=float)
Prediccion_y=Modelo_Adoptado.predict(Nuevo_Valor_x)
#Imprimimos la predicción.
print("Predicción para x:",Nuevo_Valor_x[0], ":",Prediccion_y[0][0])
Prediccion_y = Modelo_Adoptado.predict(Nuevo_Valor_x)
# Predicciones para trazar la línea de regresión
x_rangos = np.linspace(min(Valores_Entrada[:, 0]), max(Valores_Entrada[:, 0]), 100)
y_rangos = Modelo_Adoptado.predict(np.column_stack((x_rangos, np.full_like(x_rangos, Nuevo_Valor_x[0][1]))))
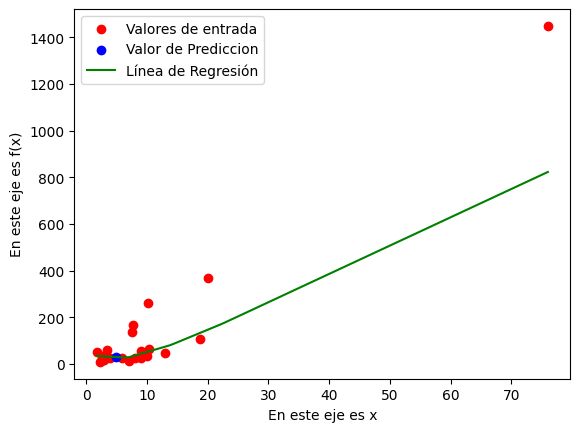
plt.scatter(Valores_Entrada[:, 0], Valores_Salida, color='red', label='Valores de entrada')
plt.scatter(Nuevo_Valor_x[:, 0], Prediccion_y, color='blue', label='Valor de Prediccion')
# Trazar la línea de regresión
plt.plot(x_rangos, y_rangos, color='green', label='Línea de Regresión')
plt.xlabel('En este eje es x')plt.ylabel('En este eje es f(x)')plt.legend()
plt.show()
"""
MODELO ADOPTADO:
<keras.engine.sequential.Sequential object at 0x7c67bc0626b0>
*************************************************************
1/1 [==============================] - 0s 49ms/step
Predicción para x: [ 5. 12.] : 29.183989
1/1 [==============================] - 0s 20ms/step
4/4 [==============================] - 0s 2ms/step
"""