A random matrix is a matrix of given type and size whose entries consist of random numbers from some specified distribution.
Random matrix theory is cited as one of the "modern tools" used in Catherine's proof of an important result in prime number theory in the 2005 film Proof.
For a real 
matrix with elements having a standard normal distribution, the expected number of real eigenvalues is given by
 |  |  | (1) |
 |  |  | (2) |
where 
is a hypergeometric function and 
is a beta function (Edelman et al. 1994, Edelman and Kostlan 1994). 
has asymptotic behavior
 | (3) |
Let 
be the probability that there are exactly 
real eigenvalues in the complex spectrum of the 
matrix. Edelman (1997) showed that
 | (4) |
which is the smallest probability of all 
s. The entire probability function of the number of expected real eigenvalues in the spectrum of a Gaussian real random matrix was derived by Kanzieper and Akemann (2005) as
 | (5) |
where
 |  |  | (6) |
 |  |  | (7) |
In (6), the summation runs over all partitions 
of length 
, 
is the number of pairs of complex-conjugated eigenvalues, and 
are zonal polynomial. In addition, (6) makes use a frequency representation of the partition 
(Kanzieper and Akemann 2005). The arguments 
depend on the parity of 
(the matrix dimension) and are given by
 | (8) |
where 
is a matrix trace, 
is an 
matrix with entries
 |  | ![int_0^inftyy^(2(beta-alpha)-1)e^(y^2)erfc(ysqrt(2))×[(2alpha+1)L_(2alpha+1)^(2(beta-alpha)-1)(-2y^2)+2y^2L_(2alpha-1)^(2(beta-alpha)+1)(-2y^2)]dy](https://mathworld.wolfram.com/images/equations/RandomMatrix/Inline33.svg) | (9) |
 |  |  | (10) |
and 
vary between 0 and 
, 
with 
the floor function), 
are generalized Laguerre polynomials, and 
is the complementary erf function erfc (Kanzieper and Akemann 2005).
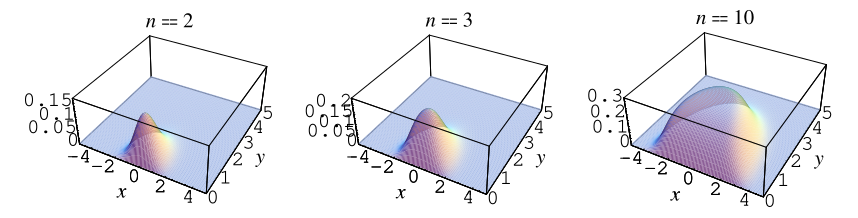
Edelman (1997) proved that the density of a random complex pair of eigenvalues 
of a real 
matrix whose elements are taken from a standard normal distribution is
 |  |  | (11) |
 |  |  | (12) |
for 
, where 
is the erfc (complementary error) function, 
is the exponential sum function, and 
is the upper incomplete gamma function. Integrating over the upper half-plane (and multiplying by 2) gives the expected number of complex eigenvalues as
 |  |  | (13) |
 |  |  | (14) |
 |  |  | (15) |
(Edelman 1997). The first few values are
 |  |  | (16) |
 |  |  | (17) |
 |  |  | (18) |
 |  |  | (19) |
 |  |  | (20) |
(OEIS A052928, A093605, and A046161).
Girko's circular law considers eigenvalues 
(possibly complex) of a set of random 
real matrices with entries independent and taken from a standard normal distribution and states that as 
, 
is uniformly distributed on the unit disk in the complex plane.
Wigner's semicircle law states that the for large 
symmetric real matrices with elements taken from a distribution satisfying certain rather general properties, the distribution of eigenvalues is the semicircle function.
If 
matrices 
are chosen with probability 1/2 from one of
 |  | ![[0 1; 1 1]](https://mathworld.wolfram.com/images/equations/RandomMatrix/Inline89.svg) | (21) |
 |  | ![[0 1; 1 -1],](https://mathworld.wolfram.com/images/equations/RandomMatrix/Inline92.svg) | (22) |
then
 | (23) |
where 
(OEIS A078416) and 
denotes the matrix spectral norm (Bougerol and Lacroix 1985, pp. 11 and 157; Viswanath 2000). This is the same constant appearing in the random Fibonacci sequence. The following Wolfram Language code can be used to estimate this constant.
With[{n = 100000}, m = Fold[Dot, IdentityMatrix[2], {{0, 1}, {1, #}}& /@ RandomChoice[{-1, 1}, {n}] ] // N; Log[Sqrt[Max[Eigenvalues[Transpose[m] . m]]]] / n ] 
." In 
Real Eigenvalues, Related Distributions, and the Circular Law." J. Multivariate Anal. 60, 203-232, 1997.Edelman, A. and Kostlan, E. "How Many Zeros of a Random Polynomial are Real?" Bull. Amer. Math. Soc. 32, 1-37, 1995.Edelman, A.; Kostlan, E.; and Shub, M. "How Many Eigenvalues of a Random Matrix are Real?" J. Amer. Math. Soc. 7, 247-267, 1994.Furstenberg, H. "Non-Commuting Random Products." Trans. Amer. Math. Soc. 108, 377-428, 1963.Furstenberg, H. and Kesten, H. "Products of Random Matrices." Ann. Math. Stat. 31, 457-469, 1960.Girko, V. L.