8
$\begingroup$

I've noticed a rather strange phenomenon (not important for my particular research, but interesting) and wouldn't be surprised if someone more versed in symbolic dynamics (i.e., just about anyone who knows what those words mean together) could easily explain it.

Consider the cat map $A$ and the Markov partition $\mathcal{R} =$ {$R_1,\dots,R_5$} shown below: 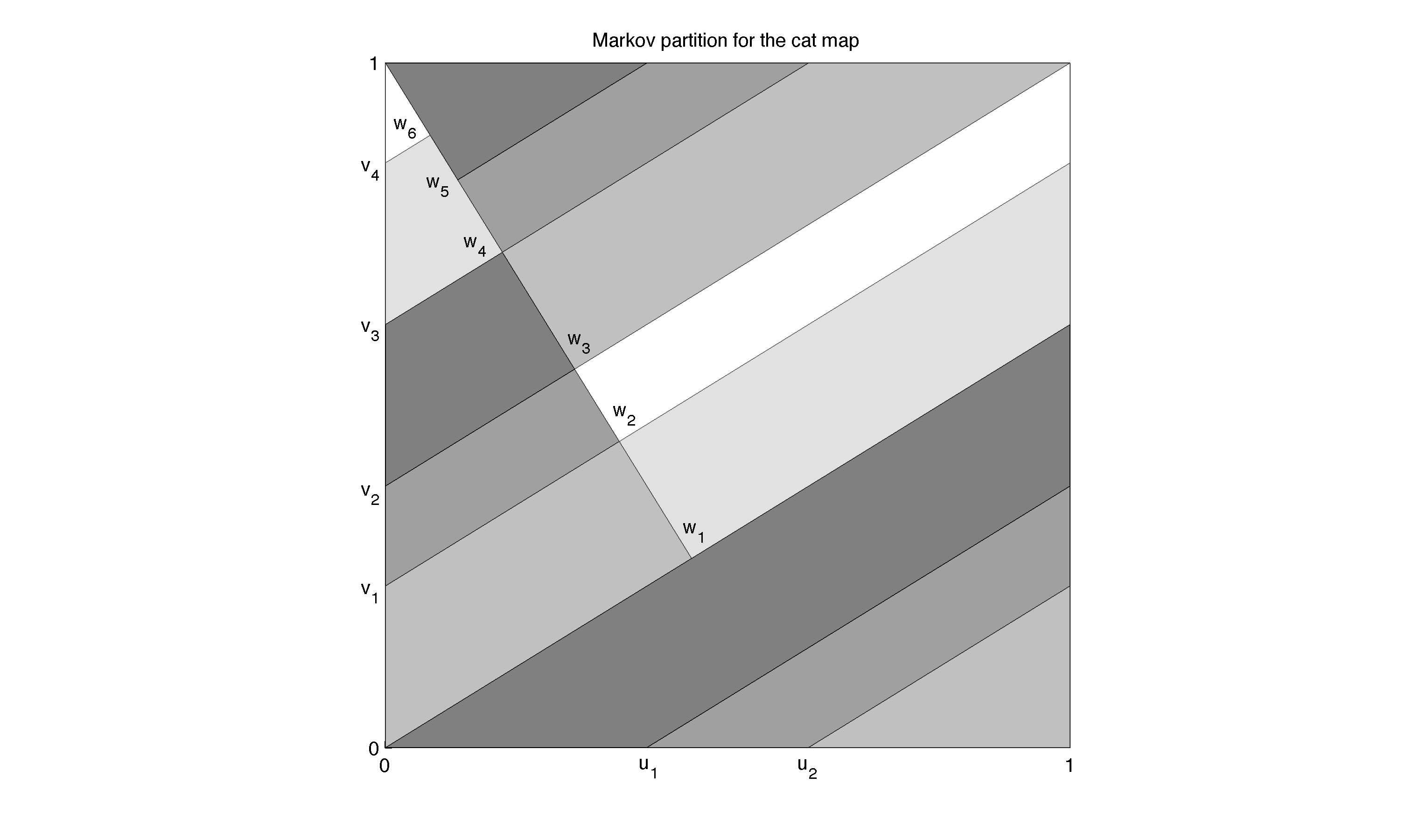alt text The rectangles in the partition are numbered from 1 (darkest) to 5 (lightest).

Now for a given initial point $x$ with rational coordinates (so that the period $t(x)$ of the sequence $A^\ell x$ is finite) consider the matrix $T(x)$ with entries $T_{jk}(x)$ equal to the cardinality of {$\ell < t(x): A^\ell x \in R_j \land A^{\ell + 1}x \in R_k$}, i.e., the number of times per period that the trajectory goes from the $j$th rectangle to the $k$th rectangle. Clearly the sparsity pattern of $T(x)$ is inherited from the matrix defining the corresponding subshift of finite type.

Let $L_q$ denote the set of rational points in $[0,1)^2$ with denominator $q$. When I compute the sum $T_{(q)} := \sum_{x \in L_q} T(x)$ I get some surprising near-equalities. For instance, with $q = 240$ I get 

 301468 0 301310 186567 0 186567 0 186407 114903 0 301310 0 301251 186407 0 0 301470 0 0 186407 0 186407 0 0 115060

and when $q = 322$ I get

 262625 0 262624 162291 0 162291 0 162312 100312 0 262624 0 262632 162312 0 0 262603 0 0 162312 0 162312 0 0 100312

The entries of each matrix are bunched around 3 values. What's more, the stochastic matrices obtained by adding unity to each entry and then row-normalizing agree to one part in a thousand.

Is there a (simple) explanation for this?

Improve this question
$\endgroup$

1 Answer 1

Reset to default
9
$\begingroup$

The reason that the matrices are alike is that, up to a multiplicative factor, each is approximately encoding $Area(T(R_i) \cap R_j))$. This is because the rational points with denominator $q$ are close being distributed across the $R_i$ in proportion to their areas. (I think you're counting these points with multiplicity equal to the period, but I don't think this makes a difference.) In particular, notice that the ratio of the three values that the entries of each matrix bunch around is about $\phi^2 : \phi : 1$, where $\phi$ is the golden ratio.

Improve this answer
$\endgroup$
2
  • $\begingroup$ Nice, I figured it would have a simple answer. Many thanks. I guess it would be straightforward to extend this to generic hyperbolic toral automorphisms since their SRB measures are all the same (viz. Lebesgue measure). $\endgroup$ Commented Dec 15, 2009 at 0:14
  • 1
    $\begingroup$ Sketch of generalization: let $f$ be an Anosov diffeomorphism on a compact manifold $M$ with SRB measure $\mu$ and Markov partition $\mathcal{R} =$ {$R_1,\dots,R_n$}. Define a stochastic matrix $P_{jk} := \mu(f(R_j) \cap R_k)$. If $X_\ell$ is a set of cardinality $\ell$ uniformly distributed w/r/t $\mu$ then the row-normalization of $T_{(X)} := \sum_{x \in X_\ell} T(x)$ converges to $P$ (presumably in measure). $\endgroup$ Commented Dec 15, 2009 at 0:28

You must log in to answer this question.

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.