This is something that has come up in my research. I originally posted this question on CrossValidated but realized it might be better suited for this site. I have deleted the question there (in case it annoys someone).
Let $X_1, X_2, \dots, $ be a sequence of iid Cauchy$(x, 1)$ random variables for some $x \in \mathbb{R}$. Define, $$ S_n(x) = \frac{\sum_{i=1}^n X_i}{\sum_{i=1}^n |X_i|},\quad n \in \mathbb{N}. $$ What, if it exists, is the limit of $S_n(x)$ as $n \to \infty$? I don't think an almost sure limit exists. Monte Carlo simulations suggest there should be a non-trivial limit. Perhaps, $S_n$ converges in distribution or in probability.
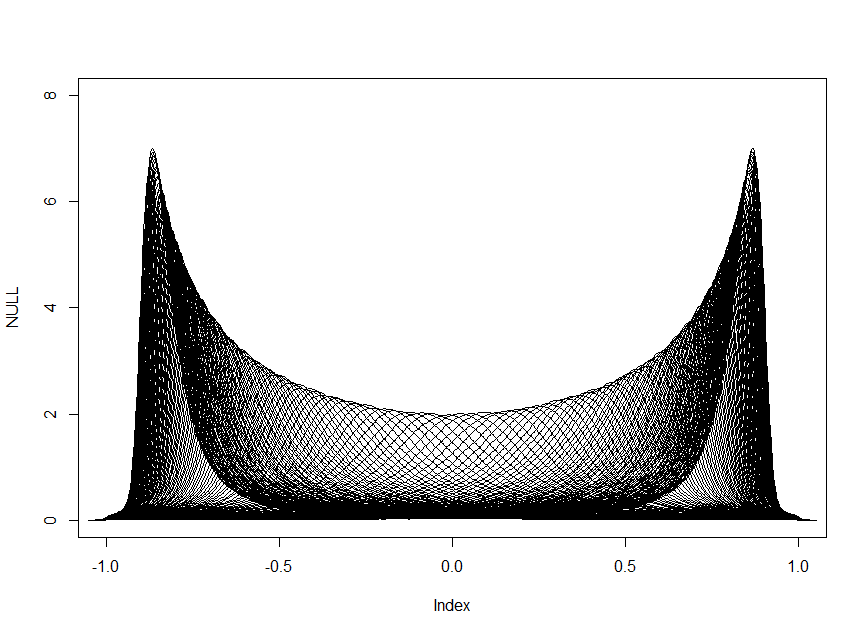
For fixed $n = 20000$, below are the density plots of $S_n(x)$ for different $x$. For each $x$, I generated $20000$ instances of $S_n(x)$ and used them to estimate the density. On the $x-$axis is the location parameter $x$.
A paper I found in an answer to another question studies the above limit for stable distributions. It conveniently ignores the Cauchy case. They cite Feller's second volume but I haven't been able to find a result there. I wonder if any references consider the above limit for Cauchy random variables.
Another excellent answer I found concerning the median of the sum of half-Cauchy random variables. I think it suggests that the half-Cauchy might somehow belong to the domain of attraction of an asymmetric $\alpha=1$ stable law. If this is so, it might help understand the limit of $S_n$. But I am not sure.