$\newcommand{\R}{\mathbb R}\newcommand{\inter}{\operatorname{int}}$The answer is yes.
Here is the proof.
The asymptotic cone of $C$ is \begin{equation*} K:=C^{as}=\{y\in\R^n\colon \exists(x_k) \text{ in }C\ \;\exists(t_k) \text{ in }\R\ \; t_k\to\infty\ \&\ x_k/t_k\to y\}. \tag{10}\label{10} \end{equation*} The polar cone to $K$ is \begin{equation*} K^\circ:=\{z\in\R^n\colon z\cdot y\le0\ \forall y\in K\}, \end{equation*} where $\cdot$ denotes the dot product.
Take any \begin{equation*} z\in\inter(K^\circ). \end{equation*} We want to show that \begin{equation*} z\overset{\text{(?)}}\in Z:=\bigcup_{x\in\partial C} \R_+\nabla f(x), \tag{20}\label{20} \end{equation*} where $\R_+w:=\{tw\colon t\in[0,\infty)\}$ for $w\in\R^n$. Clearly, without loss of generality (wlog) \begin{equation} z\ne0. \tag{30}\label{30} \end{equation}
Lemma 1: We have $z\cdot y<0$ for all $y\in K\setminus\{0\}$. (Here, as usual, $\inter$ denotes the interior of a set.)
Proof: Take any $y\in K\setminus\{0\}$. Then $z+ty\in K^\circ$ for all small enough real $t>0$, so that $z\cdot y=(z+ty)\cdot y-ty\cdot y<(z+ty)\cdot y\le0$. $\quad\Box$
Lemma 2: The supremum (say $s$) of the set $z\cdot C:=\{z\cdot x\colon x\in C\}$ is attained at some $x^*\in \partial C$, so that $z\cdot x\le s=z\cdot x^*$ for all $x\in C$.
Proof: Suppose the contrary, that the supremum of the set $z\cdot C$ is not attained. Let $(x_k)$ be a sequence in $C$ such that $z\cdot x_k\to s$.
If the sequence $(x_k)$ is bounded, then, passing to a subsequence, we see that wlog $x_k\to x^*$ for some $x^*\in\R^n$; moreover, $x^*\in C$, since the set $C$ is closed. So, $z\cdot x^*=\lim_k z\cdot x_k=s$, so that the supremum of the set $z\cdot C$ is attained, a contradiction.
So, the sequence $(x_k)$ is unbounded. So, passing to subsequences, we see that wlog $|x_k|\to \infty$ and then $x_k/|x_k|\to y$ for some $y\in\R^n\setminus\{0\}$, where $|\cdot|$ denotes the Euclidean norm. So, by \eqref{10}, $y\in K\setminus\{0\}$, and
\begin{equation} z\cdot y=\lim_k\frac{z\cdot x_k}{|x_k|}\ge0, \end{equation} since $z\cdot x_k\to s\in(-\infty,\infty]$ and $|x_k|\to\infty$. So, we get a contradiction with Lemma 1. So, the supremum of the set $z\cdot C$ is attained at the point $x^*\in C$. Finally, in view of \eqref{30}, the supremum of the set $z\cdot C$ cannot be attained at any point in $\inter C$. So, Lemma 2 is proved. $\quad\Box$
Let now $h:=\nabla f(x^*)$, so that $h\ne0$, by a condition in the OP. If $z\notin\R_+ h$, then there is some $y\in\R^n$ such that $y\cdot h<0<y\cdot z$. So, the directional derivative $y\cdot h$ of $f$ at $x^*$ in the direction of $y$ is $<0$. So, for all small enough real $t>0$ we have $f(x^*+ty)<f(x_*)\le0$ and hence $x^*+ty\in C=\{x\in\R^n\colon f(x)\le0\}$, which implies \begin{equation} z\cdot x^*=s\ge z\cdot(x^*+ty)=z\cdot x^*-tz\cdot y<z\cdot x^*, \end{equation} a contradiction.
Thus, \begin{equation} z\in\R_+ h=\R_+\nabla f(x^*)\subseteq Z, \end{equation} so that \eqref{20} holds. $\quad\Box$
One may note that, instead of the conditions $f\in\mathcal{C}^2(\R^n;\R)$ and $\forall x\in\R^n$ $\nabla f(x)\ne0$ in the OP, in the above proof we only used the weaker restriction that $f$ is differentiable on $\partial C$ with $\nabla f(x)\ne0$ for $x\in\partial C$.
Moreover, the condition that the Hessian of $f$ be positive definite everywhere was not used at all. Furthermore, note that the positive definiteness of the Hessian of $f$ implies that the set $C$ is convex -- but even the convexity of $C$ was not used in the proof.
The latter remark is illustrated in the picture below, showing (for $n=2$) the (nonconvex, light-gray) set $C\cap\big([0,2\sqrt c\,]\times[-2\sqrt c,2\sqrt c\,]\big)$ for $f=f_c$ and $c=8$, where \begin{equation} f_c(X):=g_c(y)-x,\quad g_c(y):=\sqrt{y^2+\frac{c}{1+c y^2}} \end{equation} for $X=(x,y)\in\R^2$. Shown also are the corresponding (yellow) set $K^\circ\cap\big([0,2\sqrt c\,]\times[-2\sqrt c,2\sqrt c\,]\big)$ and (orange) set $Z\cap\big([0,2\sqrt c\,]\times[-2\sqrt c,2\sqrt c\,]\big)$.
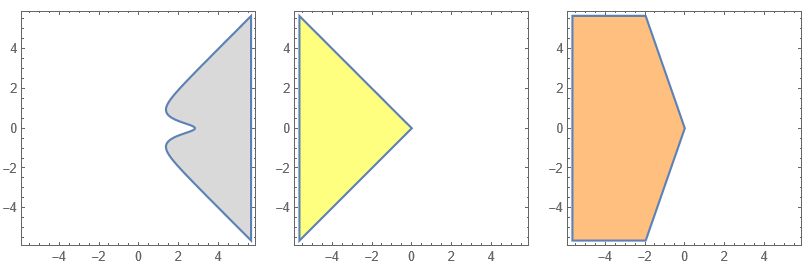
In this case, $K=\{(x,y)\in\R^2\colon|y|\le x\}$, $K^\circ=\{(x,y)\in\R^2\colon|y|\le|x|,\,x\le0\}$, $\inter(K^\circ)=\{(x,y)\in\R^2\colon|y|<|x|,\,x<0\}$, and $$Z=\{(x,y)\in\R^2\colon|y|\le k_8|x|,\,x\le0\},$$ where $k_8:=\max_{y\in\R}g'_8(y)=2.870\dots$, so that $\inter(K^\circ)\subsetneq\inter Z$.

