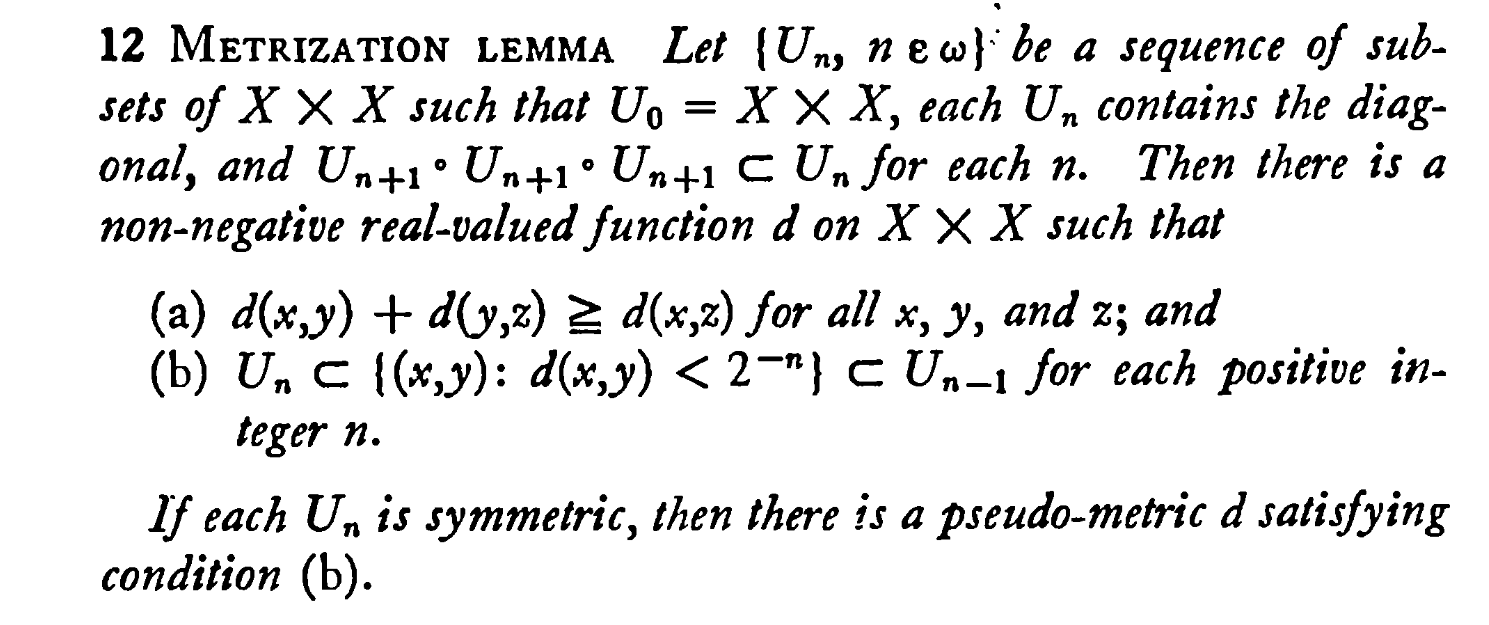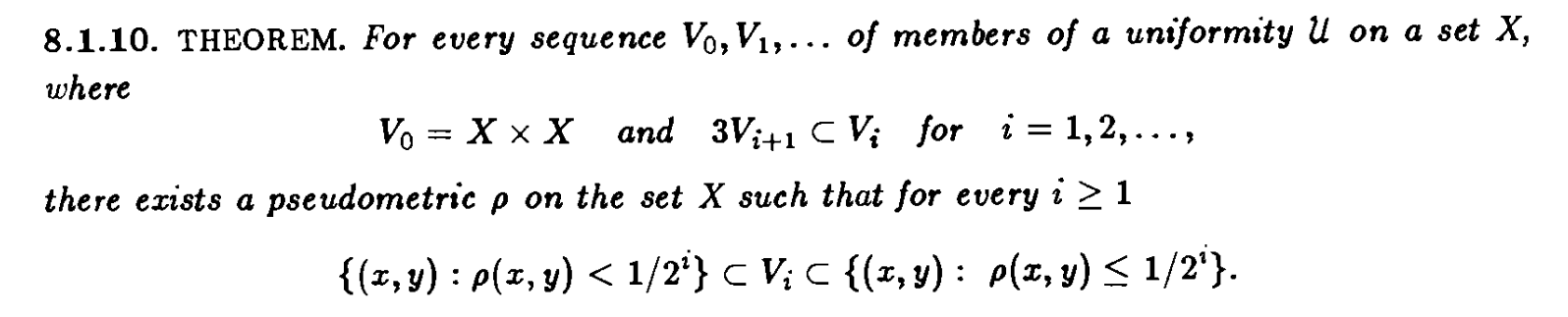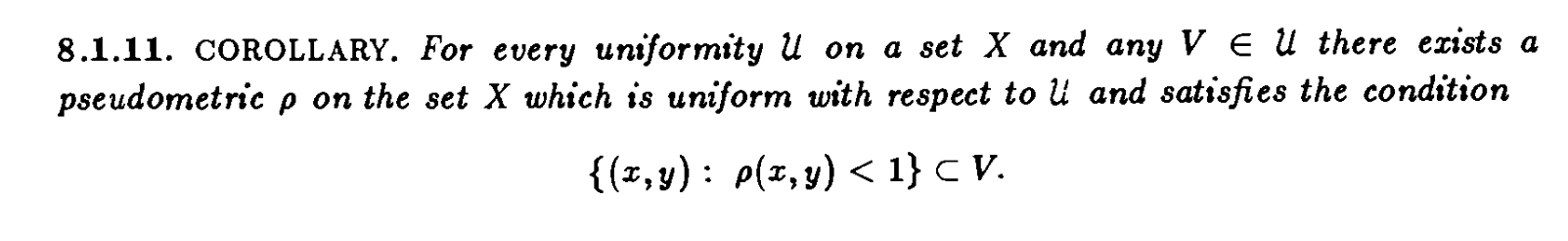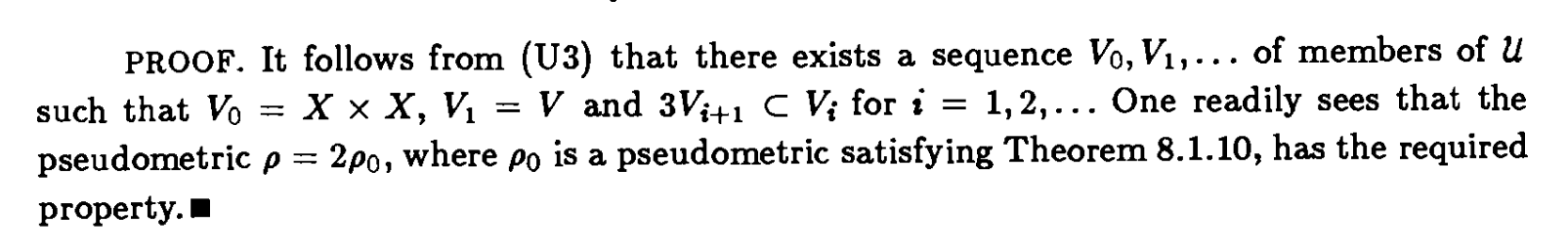The relationship between the two pseudometrics is the following: $\rho(x,y)=2\cdot d(x,y)$ for all $x$ and $y$.
We compare the definitions of the pseudometrics in both books. Both start with a sequence $\langle U_n:n\in\omega\rangle$ of sets that contain the diagonal. The demands on the sequence are: $U_0=X\times X$, and $U_{n+1}\circ U_{n+1}\circ U_{n+1}\subseteq U_n$ for all $n$.
Engelking specifies that the $U_n$ are members of a uniformity $\mathcal{U}$ and thus, according to his definition, the $U_n$ are, in addition, symmetric. Kelley imposes no further restrictions.
Kelley defines an auxiliary function $f$ on $X\times X$ by $$ f(x,y)=\begin{cases} 2^{-n} & (x,y)\in U_{n-1}\setminus U_n\\ 0 & (x,y)\in \bigcap_n U_n \end{cases} $$ and defines $d(x,y)$ to be the infimum of the set of all sums $$ \sum_{j=0}^n f(x_j,x_{j+1}) $$ over all finite sequences $\langle x_i:i\le n+1\rangle$ with $x_0=x$ and $x_{n+1}=y$.
Engelking's definition of $\rho(x,y)$ is a bit different: for every finite sequence $\langle x_i:i\le n+1\rangle$ of points in $X$ with $x_0=x$ and $x_{n+1}=y$ he takes all possible sums $$ \sum_{j=1}^{n+1} 2^{-i_j} $$ subject to $(x_{j-1},x_j)\in U_{i_j}$. One can rewrite these sums as
$$ \sum_{j=0}^{n} 2^{-i_j} $$ subject to $(x_j,x_{j+1})\in U_{i_j}$, this merely involves shifting the sequence $\langle i_j:1\le j\le n+1\rangle$ down by one.
Now observe that, in general, $(x,y)\in U_i$ iff $f(x,y)\le 2^{-(i+1)}$ Indeed: if $(x,y)\in U_i$ then $(x,y)\in U_{n-1}\setminus U_n$ for some $n$ with $n-1\ge i$, that is for some $n>i$. And that implies that $f(x,y)=2^{-n}\le2^{-(i+1)}$. Conversely, if $f(x,y)\le2^{-(i+1)}$ then $(x,y)\in U_{n-1}\setminus U_n$ for some $n\ge i+1$, that is, for some $n>i$.
This means that for every sequence $\langle x_i:i\le n+1\rangle$ and every associated sum $\sum_{j=0}^{n} 2^{-i_j}$ we have $$ 2\cdot \sum_{j=0}^n f(x_j,x_{j+1}) \le 2\cdot\sum_{j=0}^{n} 2^{-(i_j+1)} =\sum_{j=0}^{n} 2^{-i_j} $$ it also implies that $2\sum_{j=0}^n f(x_j,x_{j+1})$ is one of the associated sums, namely the one where every $i_j$ is such that $(x_j,x_{j+1})\in U_{i_j}\setminus U_{i_j+1}$.
This implies that $\rho(x,y)=2\cdot d(x,y)$ for all $x$ and $y$.