Does this non-negative function, with no stationary points, have only descent directions close to a constraint set?

Question

Suppose $P: \mathbb{R}^n \rightarrow \mathbb{R}_{\ge 0} $ is a differentiable map, with $P(x) = 0 \ \forall x \in \mathcal{X}$ and $P(x) > 0 \ \forall x \in \mathcal{X}^c$. Further, suppose $P$ has no stationary points in $\mathcal{X}^c$, i.e. $\nabla P(x) \ne 0 \ \forall x \in \mathcal{X}^c$.

My intuition is that $P$ eventually has a descent direction when we approach $\partial \mathcal{X}$ from $\mathcal{X}^c$. I need to make this more precise! For example, can we show that

$$ \forall x \in \partial \mathcal{X} ~ \exists \varepsilon >0 : \forall y \in \mathcal{X}^c ~ \lVert x-y\rVert<\varepsilon \Rightarrow \nabla P(y)^T(x-y)<0 ?$$

Here is what I thought of: For $x\in \partial \mathcal{X}$ and $y \in \mathcal{X}^c$ Taylor tells us that $$0 = P(y) + \nabla_xP(y)^\top(x-y) + o(\lVert x-y\rVert). $$ So this is almost what I need. However, I don't see that I can conclude here using $P(y) > 0$ that $$ \nabla_xP(y)^\top(x-y) < 0 $$ for $y$ close to $x$. Because, although $0 \approx P(y) + \nabla_xP(y)^\top(x-y)$, we also have that $P$ and all differentials decay to zero as we approach the boundary. I also thought about the MVT, but this doesn't seem to help since I need to keep my $y$ (as above) flexible.

It would be helpful if someone could point out whether this is obvious or whether I need additional assumptions. You may assume $\mathcal{X}$ to be compact.

Answer 1

$\newcommand\R{\mathbb R}\newcommand\ep\epsilon\newcommand\bad{\text{bad}}$One would think that the answer is "of course no, descent does not have to monotonic". However, the no stationary points condition is a strong one. So, the answer actually is "no, but the effect seems to be small and require fine tuning to be seen".

Indeed, let $n=2$, $f:=P$, and $X:=\mathcal X=\{0\}$, so that $X^c=\R^2\setminus\{0\}$. Let us seek the counterexample of the form \begin{equation*} f(r,t)=g(r)\Big(2+\sin\frac{h(r,t)}r\Big),\tag{1} \end{equation*} where $r\in(0,\infty)$ and $t\in\R$ are the polar coordinates of a point in $X^c$; $g$ is differentiable, with $g(0+)=0$, $g'>0$, and $g'(0+)=0$; and $h(r,t)$ is differentiable in $(r,t)\in X^c$ and periodic in $t$ with period $2\pi$; we also assume that $h(r,t)\to1$ uniformly in $t$ as $r\downarrow0$, so that $\sin\frac{h(r,t)}r$ in (1) is highly oscillating as $r\downarrow0$. Here we identify $X^c$ with the set $(0,\infty)\times(-\pi,\pi]$ of the pairs $(r,t)$ of polar coordinates.

The partial derivatives of $f(r,t)$ in $r$ and $t$ are \begin{equation*} f'_r(r,t)=g'(r) \Big(2+\sin\frac{h(r,t)}r\Big) \\ +\frac{g(r)}{r^2}\,(r h'_r(r,t)-h(r,t)) \cos\frac{h(r,t)}r\tag{2} \end{equation*} and \begin{equation*} f'_t(r,t)=\frac{g(r)}r\,h'_t(r,t)\cos\frac{h(r,t)}r.\tag{3} \end{equation*} We need to ensure the no stationary points condition, that is, the condition that, for any $(r,t)\in X^c$, either $f'_r(r,t)\ne0$ or $f'_t(r,t)\ne0$. If $f'_t(r,t)=0$ for some $(r,t)\in X^c$, then either (i) $\cos\frac{h(r,t)}r=0$ or (ii) $h'_t(r,t)=0$. In case (i), $f'_r(r,t)=g'(r) \big(2+\sin\frac{h(r,t)}r\big)>0$.

Consider now case (ii), which will necessarily occur for each real $r>0$, at least for two values of $t\in(-\pi,\pi]$, where the maximum and minimum of $h(r,t)$ in $t$ occur. Note that \begin{equation*} k:=\max_{t\in(-\pi,\pi]}\Big|\frac{\cos u}{2+\sin u}\Big|=\frac1{\sqrt3},\tag{4} \end{equation*} with the maximum attained at $u\in\{-\pi/6,-5\pi/6\}$. So, by (2), for $f'_r(r,t)\ne0$ it is enough that \begin{equation*} \frac{r^2g'(r)}{g(r)}>\max_{t\in(-\pi,\pi]}|r h'_r(r,t)-h(r,t)| \tag{5} \end{equation*} (for real $r>0$). At the points $t$ where the extrema of $|h(r,t)|$ in $t$ occur, we have $r h'_r(r,t)=0$ and hence $|r h'_r(r,t)-h(r,t)|=|h(r,t)|$. At all points $(r,t)\in X^c$ with such $t$, we want $h'_r(r,t)$ to have the same sign as $h(r,t)$, to make the restriction (5) as weak as possible.

Certain considerations suggest that it may make sense to define the differentiable $2\pi$-periodic in $t$ function $h$ by the formula \begin{equation*} h(r,t):=1-\frac{r^2}{1+r^2}\, t^2 (\pi -| t| )^2\tag{6} \end{equation*} for $t\in(-\pi,\pi]$. Then case (ii) $h'_t(r,t)=0$ (for $t\in(-\pi,\pi]$) means that $t\in\{0,\pi\}$, and \begin{equation*} f'_r(r,t)\big|_{t\in\{0,\pi\}}=g'(r) \Big(2+\sin\frac1r\Big) -\frac{g(r)}{r^2}\,\cos\frac1r.\tag{7} \end{equation*} If $g$ solves the ODE $g'(r)=k\frac{g(r)}{r^2}$ (with $k$ as in (4)) -- e.g. when $g(r)=e^{-k/r}$, then, by (7), we will have $f'_r(r,t)\ge0$. Now, to ensure that $f'_r(r,t)>0$ (still in case (ii) $h'_t(r,t)=0$), it is enough to let \begin{equation*} g(r):=(1+cr)e^{-k/r} \end{equation*} for any fixed real $c>0$ and all real $r>0$. Indeed, then \begin{equation*} r^2e^{k/r}\,f'_r(r,t)\big|_{t\in\{0,\pi\}} \\ = \Big(2+\sin\frac1r\Big) (k(1+cr)r+c r^2)-(1+c r) \cos\frac1r \\ \ge\Big(2+\sin\frac1r\Big)c r^2>0.\tag{8} \end{equation*} Thus, we have a nonnegative differentiable function on $\R^2$ vanishing only on $X=\{0\}$, with no stationary points in $X^c$.

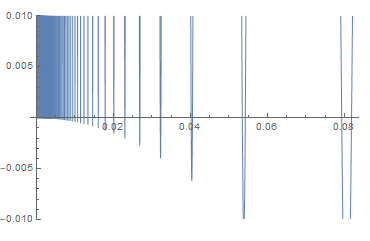
On the other hand, \begin{equation*} \bad(r):=f'_r(r,1)\,\frac{kr^2 e^{k/r}}{k + c k r + c r^2} \\ = k(2+\sin u_r) -q(r) \cos u_r,\tag{9} \end{equation*} where \begin{equation*} u_r:=\frac1r-\frac{(\pi -1)^2 r}{1+r^2}\sim\frac1r\tag{10} \end{equation*} and \begin{equation*} q(r):=\frac{k (1+(3-2 \pi +\pi ^2) r^2-(\pi -2) \pi r^4) (c r+1)}{(1+r^2)^2(c k r+c r^2+k)} \\ =1+((\pi -1)^2-c\sqrt3) r^2+O(r^3) \end{equation*} as ($r\downarrow0$), so that \begin{equation*} q(r)>1+4r^2>1\tag{11} \end{equation*} eventually (that is, for all small enough $r>0$) if $c=1/10$ (say).

Moreover, in view of (10), the equation $u_r=-\pi/6+2\pi m$ has solutions $r_m\sim1/(2\pi m)$ for all large enough natural $m$. So (cf. (4)), for such $m$, by (11),
\begin{equation*} \bad(r_m)= \frac{\sqrt3}2(1-q(r_m))<-\frac{\sqrt3}2\,4r_m^2<0, \end{equation*} whence, by (9), the radial derivative $f'_r(r_m,1)$ is strictly negative, whereas $r_m\downarrow0$. $\Box$

---

Here is the graph $\{(r,\bad(r))\colon0<r<1/10,-1/100<\bad(r)<1/100\}$:

Answer 2

Set for instance, in polar coordinates: $$P(r,\theta):=e^{-\frac1{4r}}\Big(2+\cos\big(\theta+\frac1r\big)\Big).$$ It is quickly checked that this defines a $C^\infty$ function on $\mathbb{R^2}$ which is strictly positive on $\mathbb{R^2}\setminus\{0\}$ and vanishes at the origin, with $ \partial_r P $ changing sign in any nbd of the origin, and such that $\nabla P$ vanishes only on the origin (if $r>0$, and $\partial_\theta P$ vanishes, certainly $\partial_r P$ does not).