Given a random symmetric matrix $M$ and two numbers $\lambda_\min$ and $\lambda_\max$ how do we calculate the expected or high probability value of the fraction of its eigenvalues which lie in the interval $[\lambda_{\min},\lambda_{\max}]$?
I would like to know of references which might have achieved such an estimate for even any specific distribution of $M$
In particular I am most curious about the case when $M$ is random PSD, $\lambda_\min =0$ and $\lambda_{\max} \lll \Vert M \Vert_2$
A random PSD matrix $M$ can be constructed by taking $M=WW^T$, with the $n\times n$ matrix elements of $W$ i.i.d. with mean zero and variance $\sigma^2$. For $n\gg 1$ the marginal distribution $\rho(\lambda)$ of the eigenvalues $\lambda$ of $W$ is given by the Marcenko-Pastur distribution $$\rho(\lambda)=\frac{1}{2\pi\sigma^2 n}\sqrt{\frac{4n\sigma^2 }{\lambda}-1},\;\;0<\lambda<4n\sigma^2 ,$$ and then you can integrate from $0$ to $\lambda_{\rm max}<4n\sigma^2 $ to obtain the desired fraction $f$ of eigenvalues in the interval $(0,\lambda_{\rm max})$, $$f=\frac{\sqrt{\lambda_{\rm max} \left(4 n {\sigma}^2-\lambda_{\rm max}\right)}}{2 \pi n {\sigma}^2}-\frac{2 \arctan\left(\sqrt{\frac{4 n {\sigma}^2}{\lambda_{\rm max}}-1}\right)}{\pi }+1.$$
For $\lambda_{\rm max}\ll 4n\sigma^2$ this has the asymptotics $$f\rightarrow\frac{2}{\pi}\sqrt{\lambda_{\rm max}}.$$
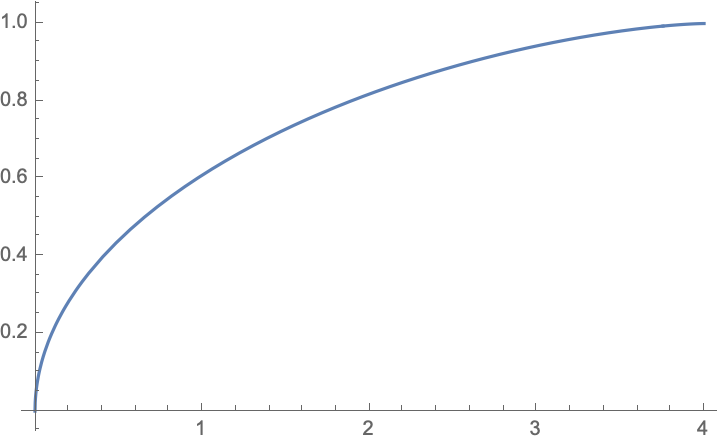
$f$ versus $\lambda_{\rm max}/n\sigma^2$.
The $\sqrt\lambda_{\rm max}$ growth is generic for random PSD matrices. It arises because eigenvalue repulsion causes a $1/\sqrt\lambda$ accumulation of the eigenvalues near the hard spectral edge at $\lambda=0$.
