11
$\begingroup$

Let $g(x)$ be a non-negative function supported on $[0,1]$. Let $g \ast g$ denote the convolution of $g$ with itself. Question: What is the smallest possible $L^1(0,1)$ norm of $g$, if I require that $(g \ast g) (t) \geq 1$ for all $t \in [0,1]$.

Clearly one needs $\|g\|_1 \geq 1$. However, $\|g\|_1=1$ cannot be achieved. But what is the best value that can actually be achieved?

(Maybe the optimizing function is explicitly known? Something like $g(x) = 1/\sqrt{\pi x}$ works and gives $\|g\|_1 \approx 1.13$, but probably something smaller is possible.)

Improve this question
$\endgroup$
5
  • 2
    $\begingroup$ Interestingly, exactly the same norm $\|g\|_1 = 2/\sqrt{\pi} \approx 1.13$ is attained both by $g(x) = (\pi x)^{-1/2}$ and by $g(x) = \max\{(\pi x)^{-1/2},(\pi (1/2-x))^{-1/2}\} \mathbb{1}_{(0,1/2)}(x)$. $\endgroup$ Commented Sep 30, 2019 at 7:22
  • $\begingroup$ Silly question. Is the reason that the L_1 norm lower bound of 1 cannot be achieved the normalization of the Fourier transform on [0,1]? $\endgroup$ Commented Sep 30, 2019 at 21:47
  • $\begingroup$ The Fourier transform of an indicator function is not non-negative real. In contrast, a convolution of a function with itself leads to a non-negative real Fourier transform (since we are squaring). So 1 cannot be reached exactly. However, I don't have an estimate how close to 1 one can actually get. $\endgroup$ Commented Oct 1, 2019 at 8:06
  • $\begingroup$ Sorry for being silly, but which consequences you make from squaring a complex-valued function? $\endgroup$ Commented Oct 1, 2019 at 8:45
  • 1
    $\begingroup$ I would rather say that the Laplace transform of the uniform distribution is not a square of an entire function, due to the behaviour at zeroes. $\endgroup$ Commented Oct 1, 2019 at 8:49

2 Answers 2

Reset to default
5
$\begingroup$

Rick Barnard and I looked at the same problem for the auto-convolution instead of the convolution: arXiv. Our constants are a bit worse because you basically need two square-root singularities, one on each side. These types of inequalities tend to be relevant in combinatorics and they tend to be pretty hard (we discuss some in our paper). One I like a lot can be found in this MO post. (I would have commented but you need 50 reputation for that, sorry.)

Improve this answer
$\endgroup$
4
$\begingroup$

(Too long for a comment.)

Numerical experiments suggests that one cannot do better than $1 / \sqrt{\pi x}$ (or one of the equivalent variants, the set of minimizers appears to be quite large). Here is a plot of three minimizers obtained numerically for the discrete analogue of the problem on $\{0, 1, 2, \ldots, n - 1\}$ with $n = 75$. These minimizers were found by Mathematica with three different numerical optimization methods (blue: "DifferentialEvolution", yellow: "NelderMead", green: "SimmulatedAnnealing"). The corresponding norms are 1.12145, 1.12842, 1.1265, respectively.

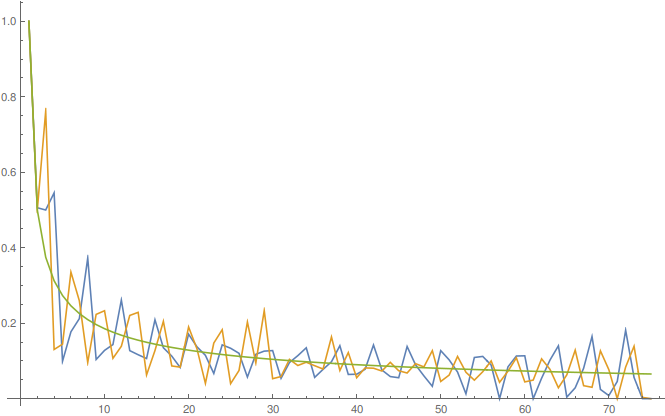
enter image description here

Mathematica code:

n = 75; expr = Sum[x[i], {i, 0, n - 1}]/Sqrt[n]; constr = Join[ Table[Sum[x[j] x[i - j], {j, 0, i}] >= 1, {i, 0, n - 1}], Table[x[i] >= 0, {i, 0, n - 1}]]; vars = Table[x[i], {i, 0, n - 1}]; {min1, subst1} = NMinimize[{expr, constr}, vars, Method -> "DifferentialEvolution"]; {min2, subst2} = NMinimize[{expr, constr}, vars, Method -> "NelderMead"]; {min3, subst3} = NMinimize[{expr, constr}, vars, Method -> "SimulatedAnnealing"]; {min1, min2, min3} ListPlot[{vars /. subst1, vars /. subst2, vars /. subst3}, Joined -> True, PlotRange -> All]
Improve this answer
$\endgroup$
10
  • $\begingroup$ Have you found any other minimizers in an analytical form? $\endgroup$ Commented Oct 1, 2019 at 10:42
  • $\begingroup$ I have not tried that, but apparently one can find intermediate solutions between the two that I mentioned in my comment. If I find time later today, I will see if I can figure out the details. $\endgroup$ Commented Oct 1, 2019 at 11:51
  • $\begingroup$ I am not quite sure if that has any real significance. The numerical values I get using the same code for n=85 are {1.12831, 1.12672, 1.1287}, and for n=95 they are {1.12594, 1.13249, 1.1269}. In comparison, $2 / \sqrt{\pi} \approx 1.1284$. $\endgroup$ Commented Oct 1, 2019 at 12:18
  • $\begingroup$ Note that $x_k = \tfrac{1 \cdot 3 \cdot 5 \cdots (2k-1)}{2 \cdot 4 \cdot 6 \cdots 2k}$ solves $\sum_{j=0}^i x_j x_{i-j}=1$ exactly and has the same asymptotic $2\sqrt{n}/\sqrt{\pi}$. However, your data suggests that it is possible to improve on this a little for finite $n$. $\endgroup$ Commented Oct 2, 2019 at 21:07
  • $\begingroup$ @DavidESpeyer: This explicit solution corresponds to the green line in the plot, I believe. I am not sure if one can really improve upon this, differences between minimizers found by different algorithms seem to be within the range of admissible error. $\endgroup$ Commented Oct 2, 2019 at 21:16

You must log in to answer this question.

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.