Python code for abnormal detection or fault detection using Support Vector Data Description (SVDD)
Version 1.1, 11-NOV-2021
Email: iqiukp@outlook.com
- SVDD BaseEstimator based on sklearn.base for one-class or binary classification
- Multiple kinds of kernel functions (linear, gaussian, polynomial, sigmoid)
- Visualization of decision boundaries for 2D data
- cvxopt
- matplotlib
- numpy
- scikit_learn
- scikit-opt (optional, only used for parameter optimization)
- The label must be 1 for positive sample or -1 for negative sample.
- Detailed applications please see the examples.
- This code is for reference only.
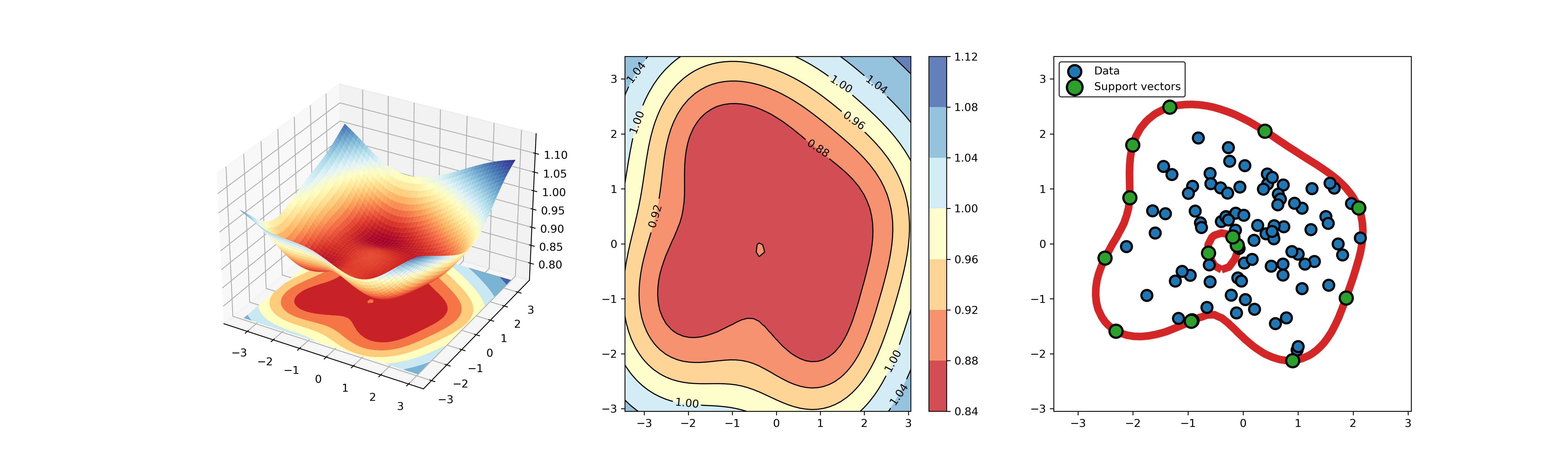
An example for SVDD model fitting using unlabeled data.
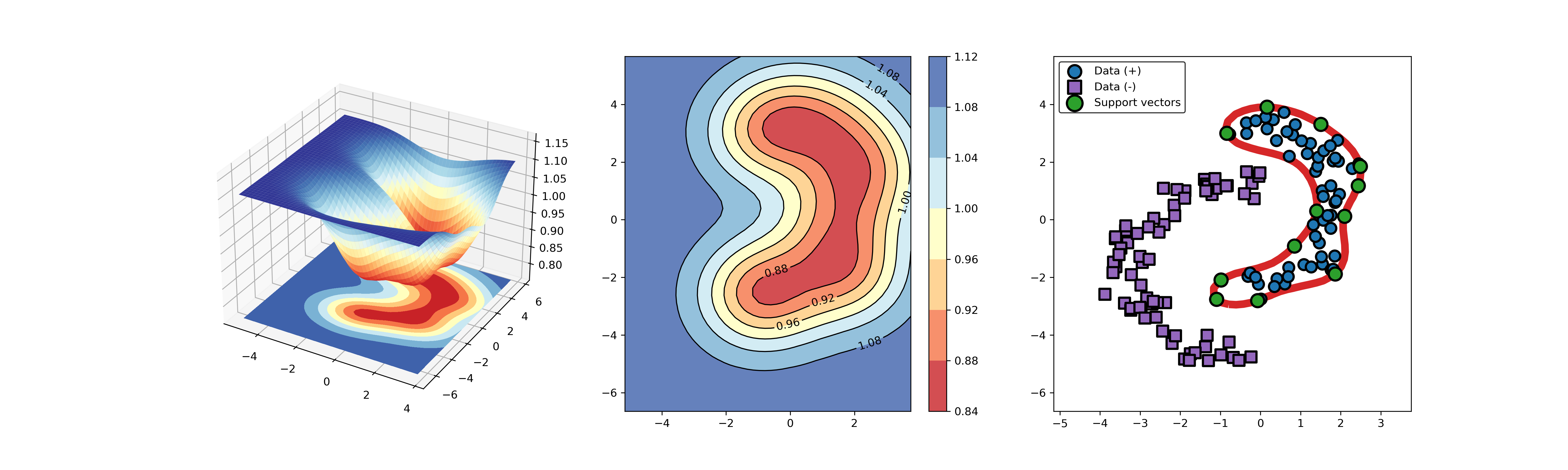
An example for SVDD model fitting with negataive samples.
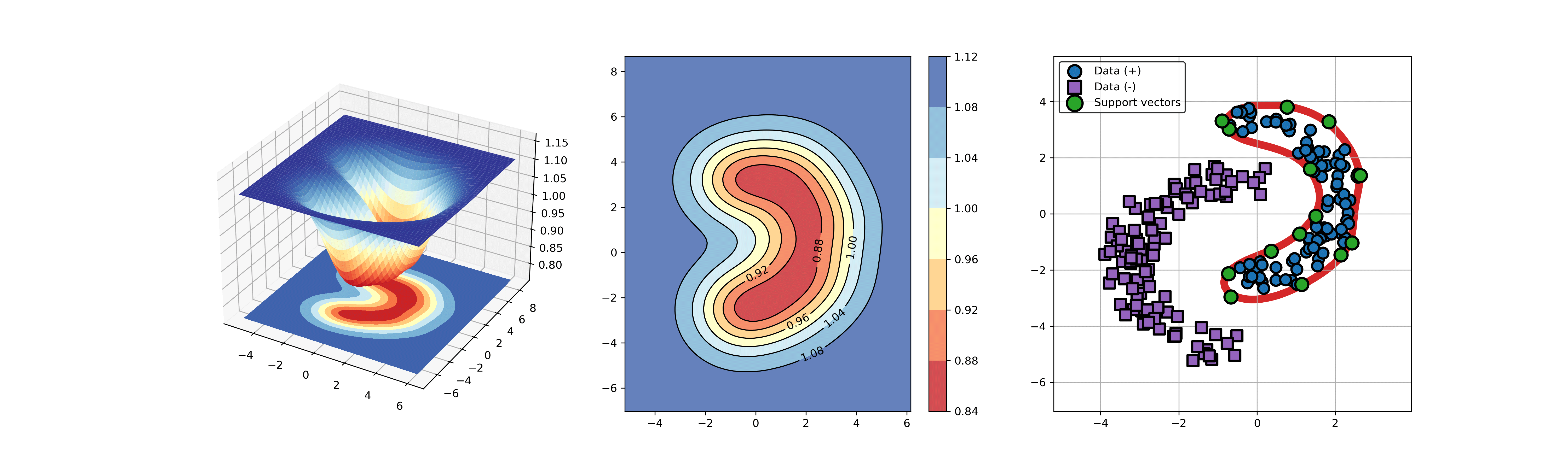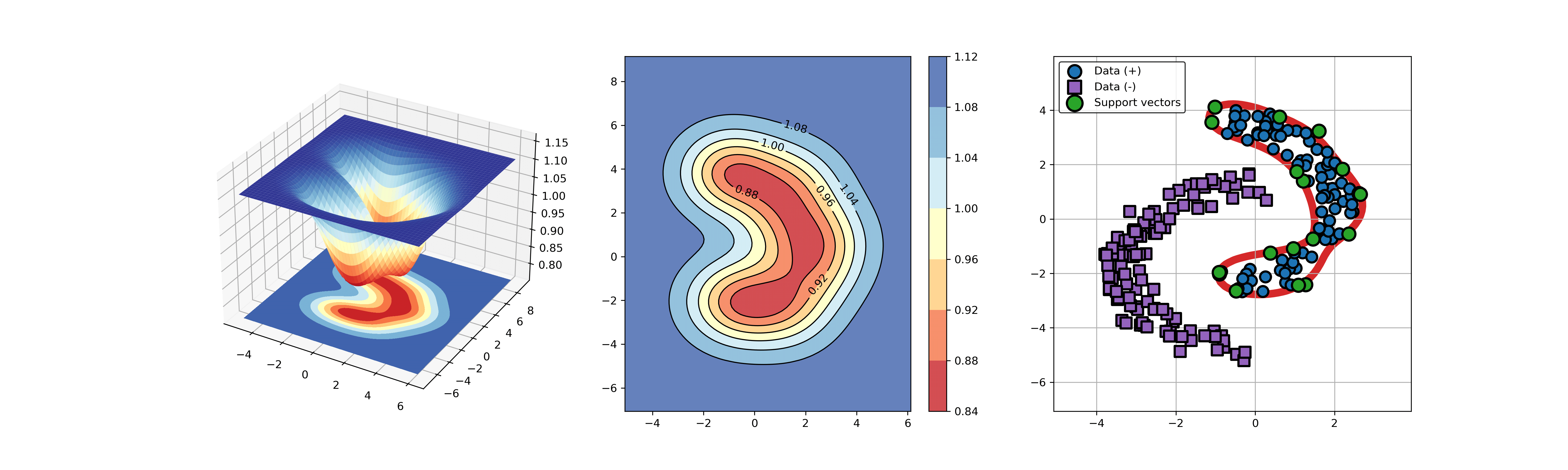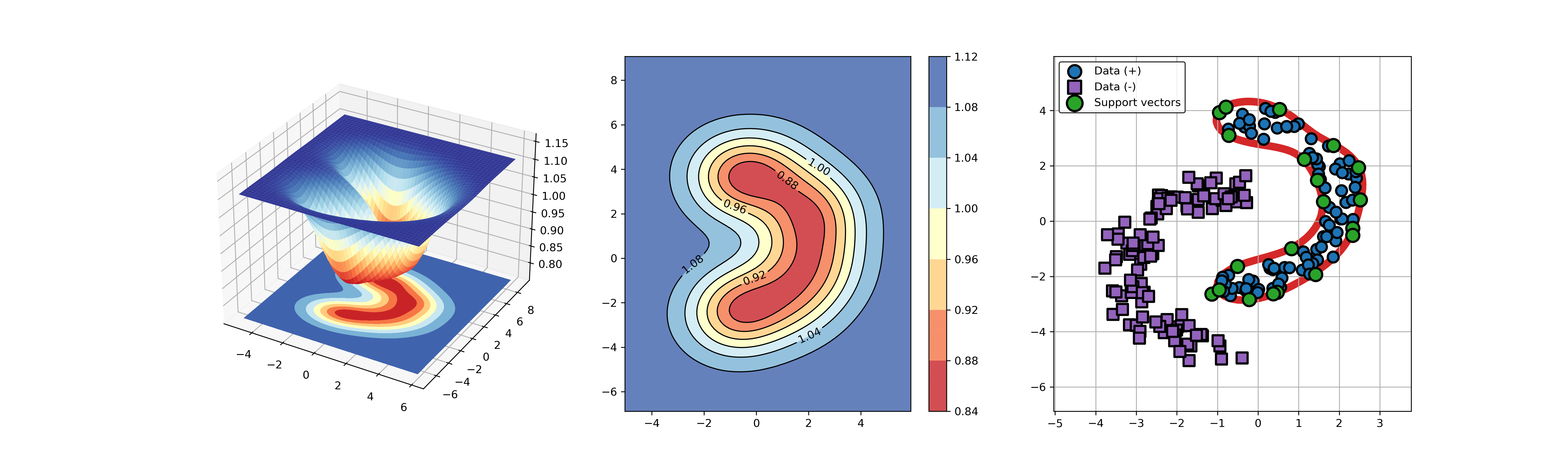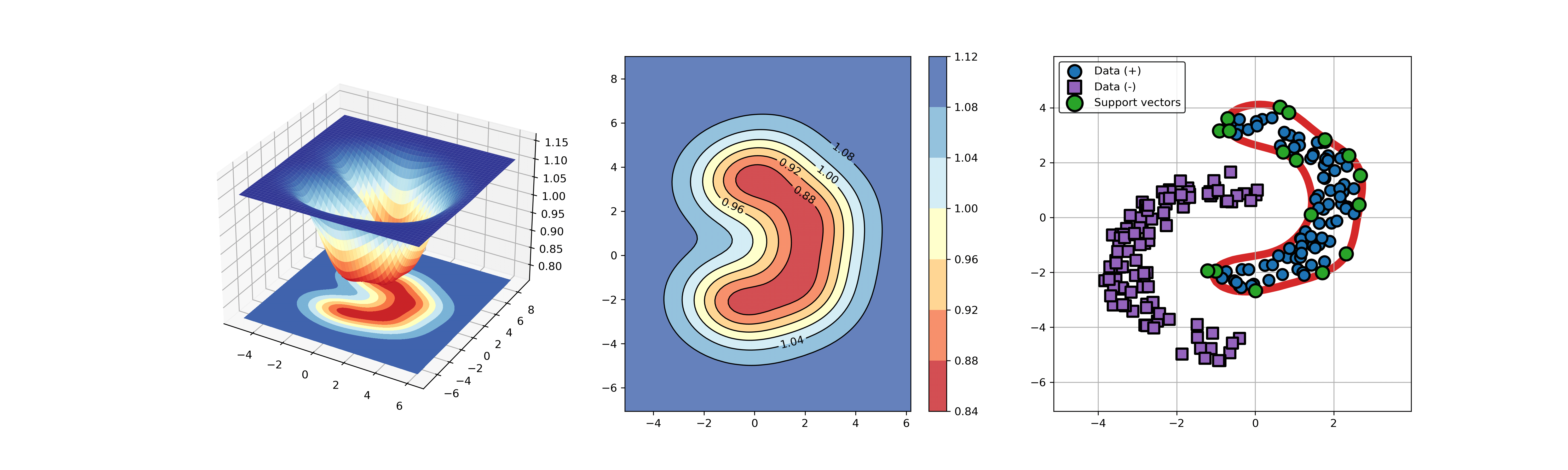
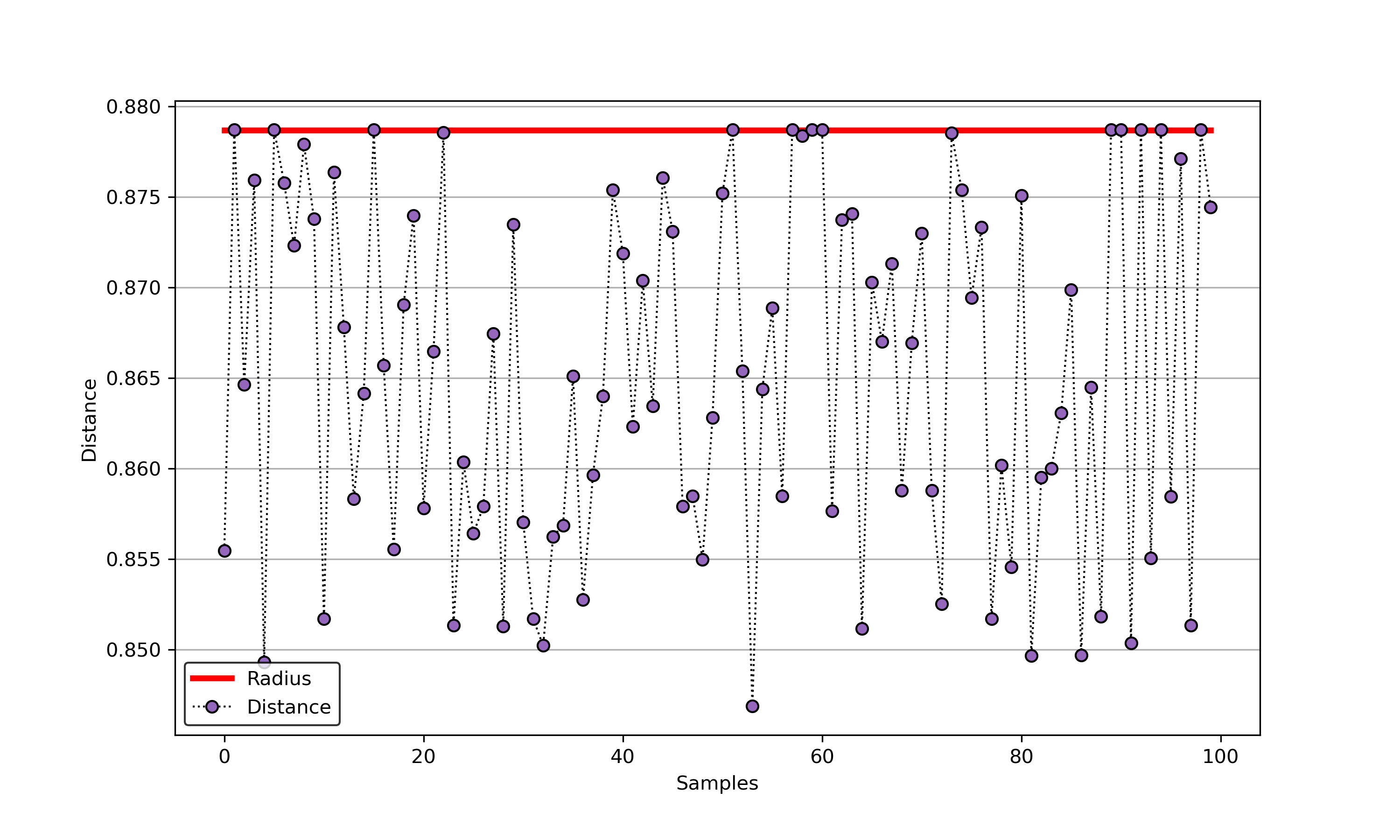
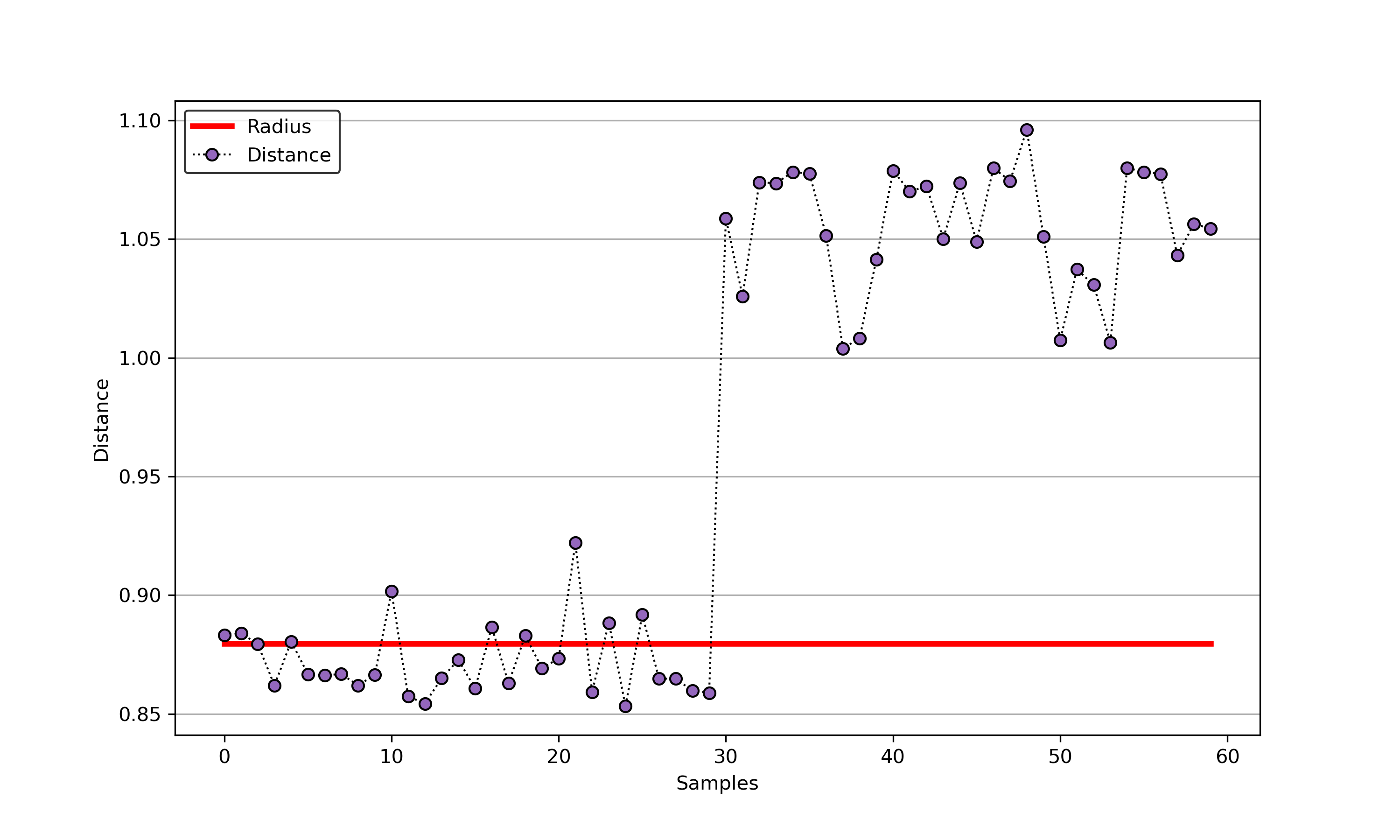
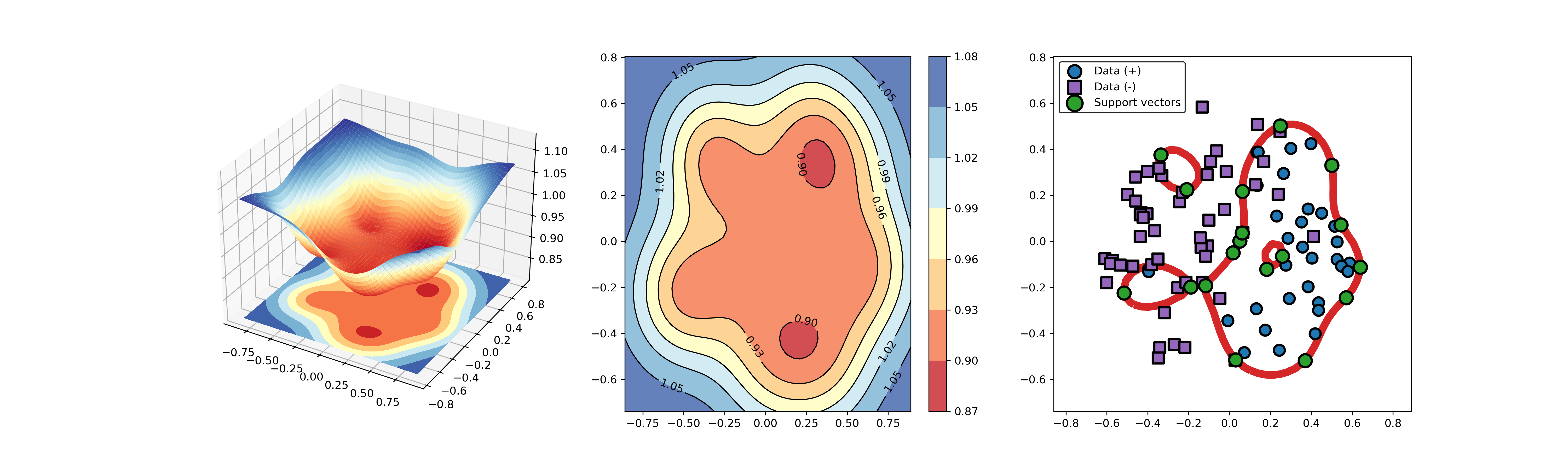
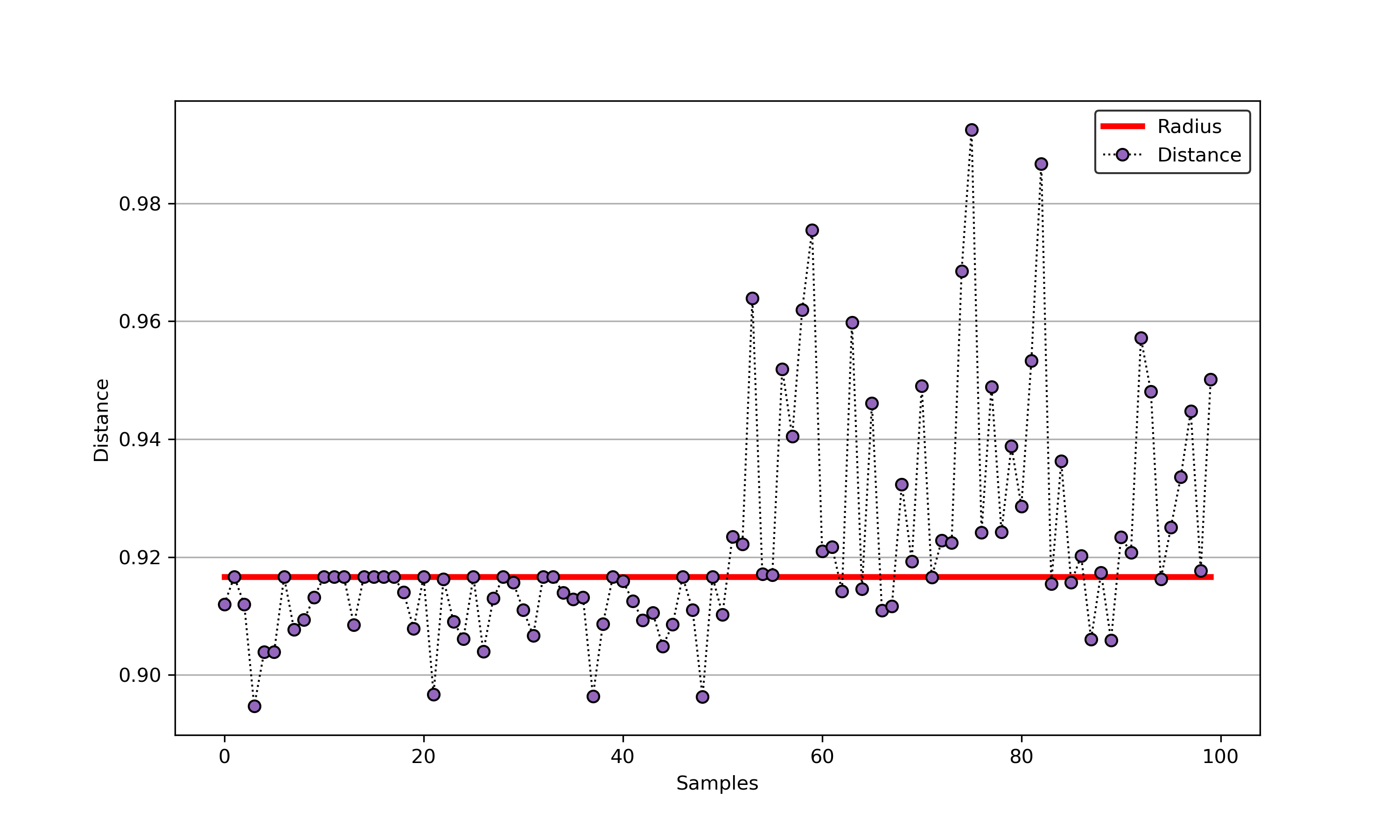
import sys sys.path.append("..") from sklearn.datasets import load_wine from src.BaseSVDD import BaseSVDD, BananaDataset # Banana-shaped dataset generation and partitioning X, y = BananaDataset.generate(number=100, display='on') X_train, X_test, y_train, y_test = BananaDataset.split(X, y, ratio=0.3) # svdd = BaseSVDD(C=0.9, gamma=0.3, kernel='rbf', display='on') # svdd.fit(X_train, y_train) # svdd.plot_boundary(X_train, y_train) # y_test_predict = svdd.predict(X_test, y_test) # radius = svdd.radius distance = svdd.get_distance(X_test) svdd.plot_distance(radius, distance)An example for SVDD model fitting using different kernels.
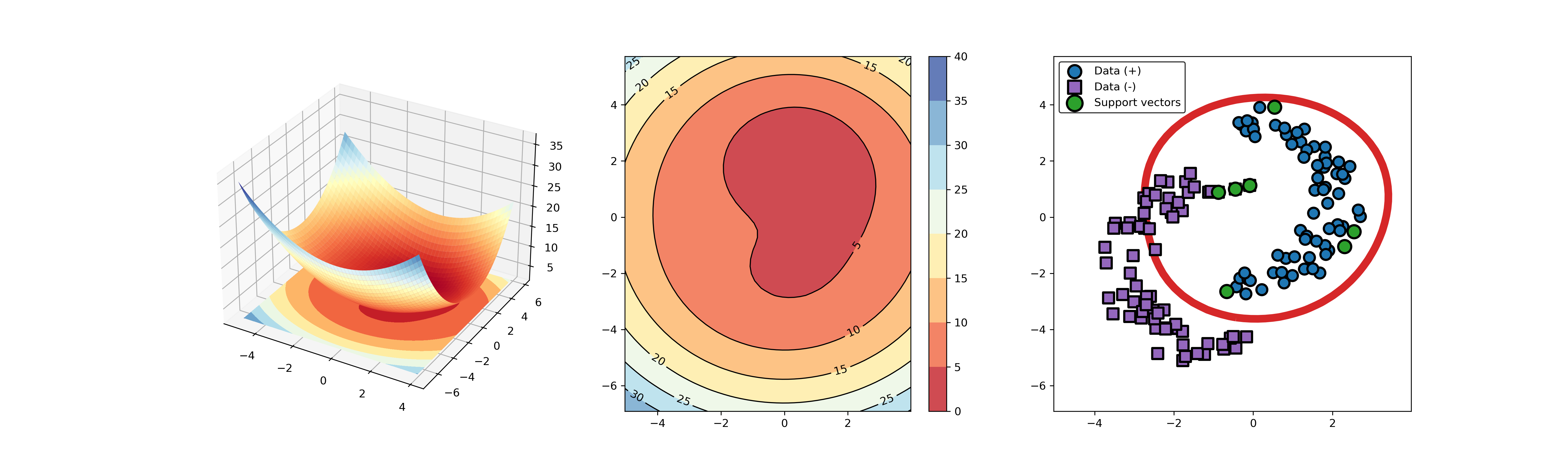
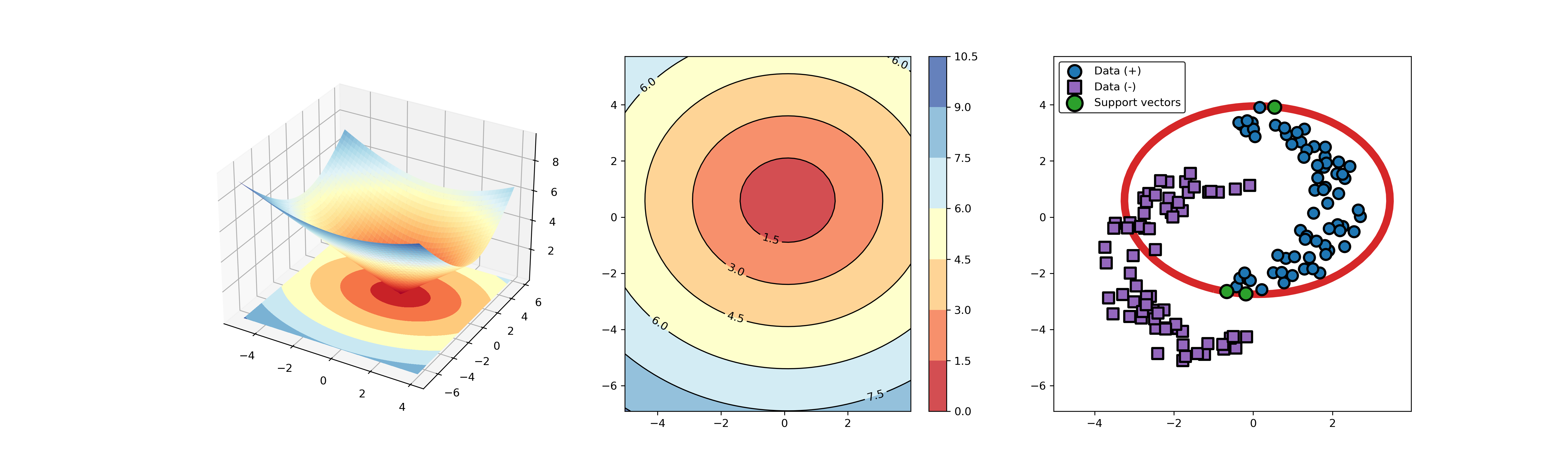
import sys sys.path.append("..") from src.BaseSVDD import BaseSVDD, BananaDataset # Banana-shaped dataset generation and partitioning X, y = BananaDataset.generate(number=100, display='on') X_train, X_test, y_train, y_test = BananaDataset.split(X, y, ratio=0.3) # kernel list kernelList = {"1": BaseSVDD(C=0.9, kernel='rbf', gamma=0.3, display='on'), "2": BaseSVDD(C=0.9, kernel='poly',degree=2, display='on'), "3": BaseSVDD(C=0.9, kernel='linear', display='on') } # for i in range(len(kernelList)): svdd = kernelList.get(str(i+1)) svdd.fit(X_train, y_train) svdd.plot_boundary(X_train, y_train)An example for SVDD model fitting using nonlinear principal component.
The KPCA algorithm is used to reduce the dimension of the original data.
import sys sys.path.append("..") import numpy as np from src.BaseSVDD import BaseSVDD from sklearn.decomposition import KernelPCA # create 100 points with 5 dimensions X = np.r_[np.random.randn(50, 5) + 1, np.random.randn(50, 5)] y = np.append(np.ones((50, 1), dtype=np.int64), -np.ones((50, 1), dtype=np.int64), axis=0) # number of the dimensionality kpca = KernelPCA(n_components=2, kernel="rbf", gamma=0.1, fit_inverse_transform=True) X_kpca = kpca.fit_transform(X) # fit the SVDD model svdd = BaseSVDD(C=0.9, gamma=10, kernel='rbf', display='on') # fit and predict svdd.fit(X_kpca, y) y_test_predict = svdd.predict(X_kpca, y) # plot the distance curve radius = svdd.radius distance = svdd.get_distance(X_kpca) svdd.plot_distance(radius, distance) # plot the boundary svdd.plot_boundary(X_kpca, y)An example for parameter optimization using PSO.
"scikit-opt" is required in this example.
https://github.com/guofei9987/scikit-opt
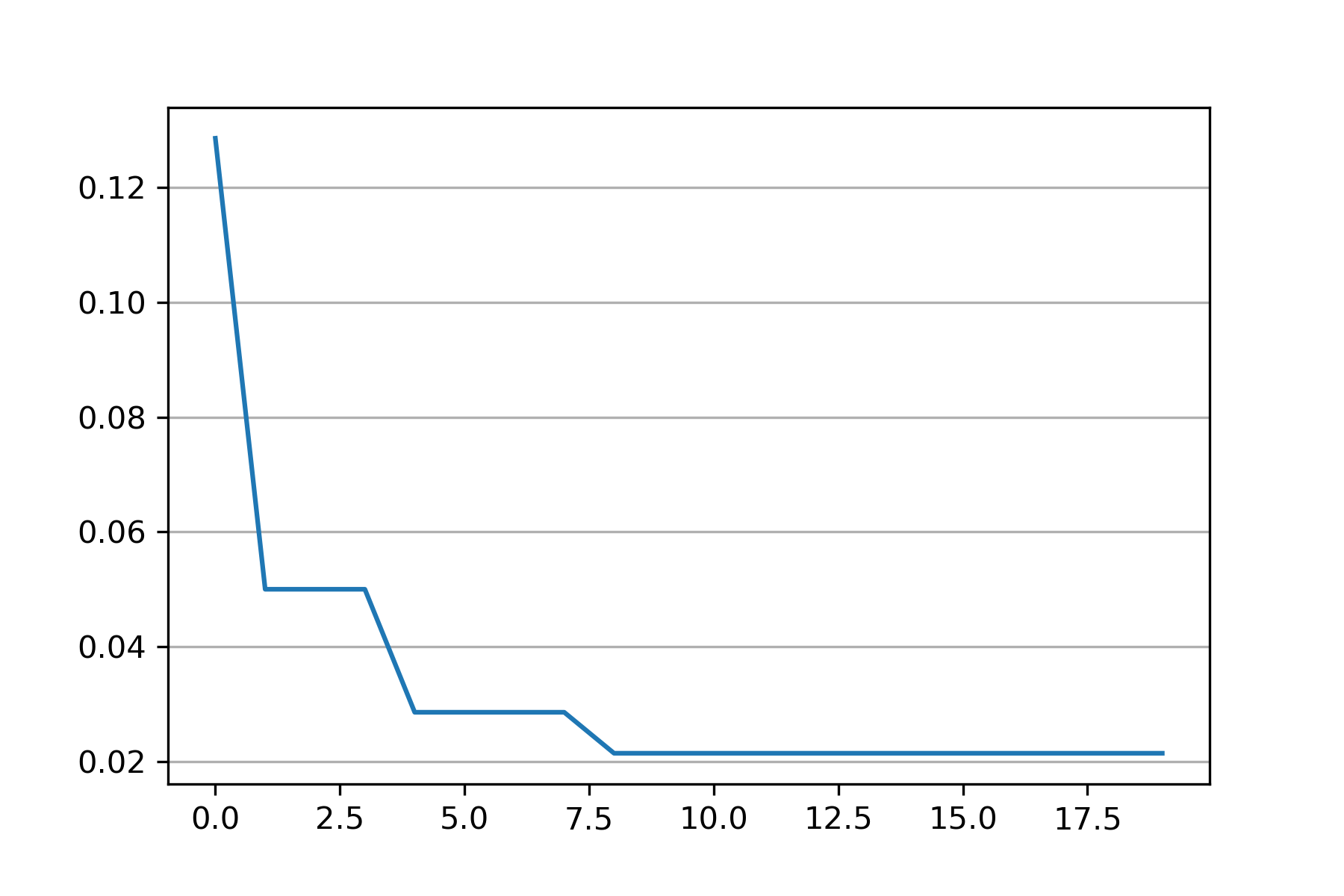
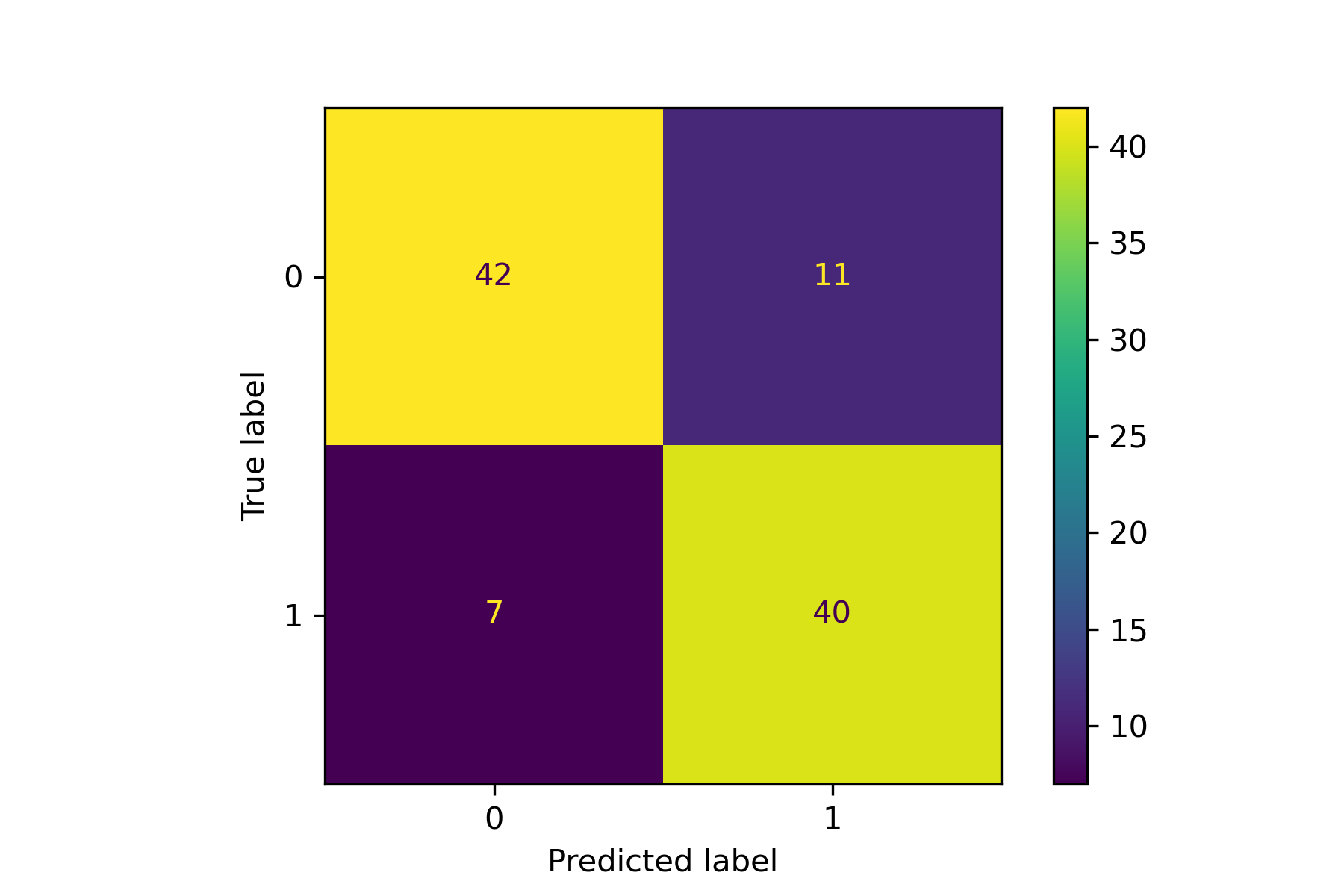
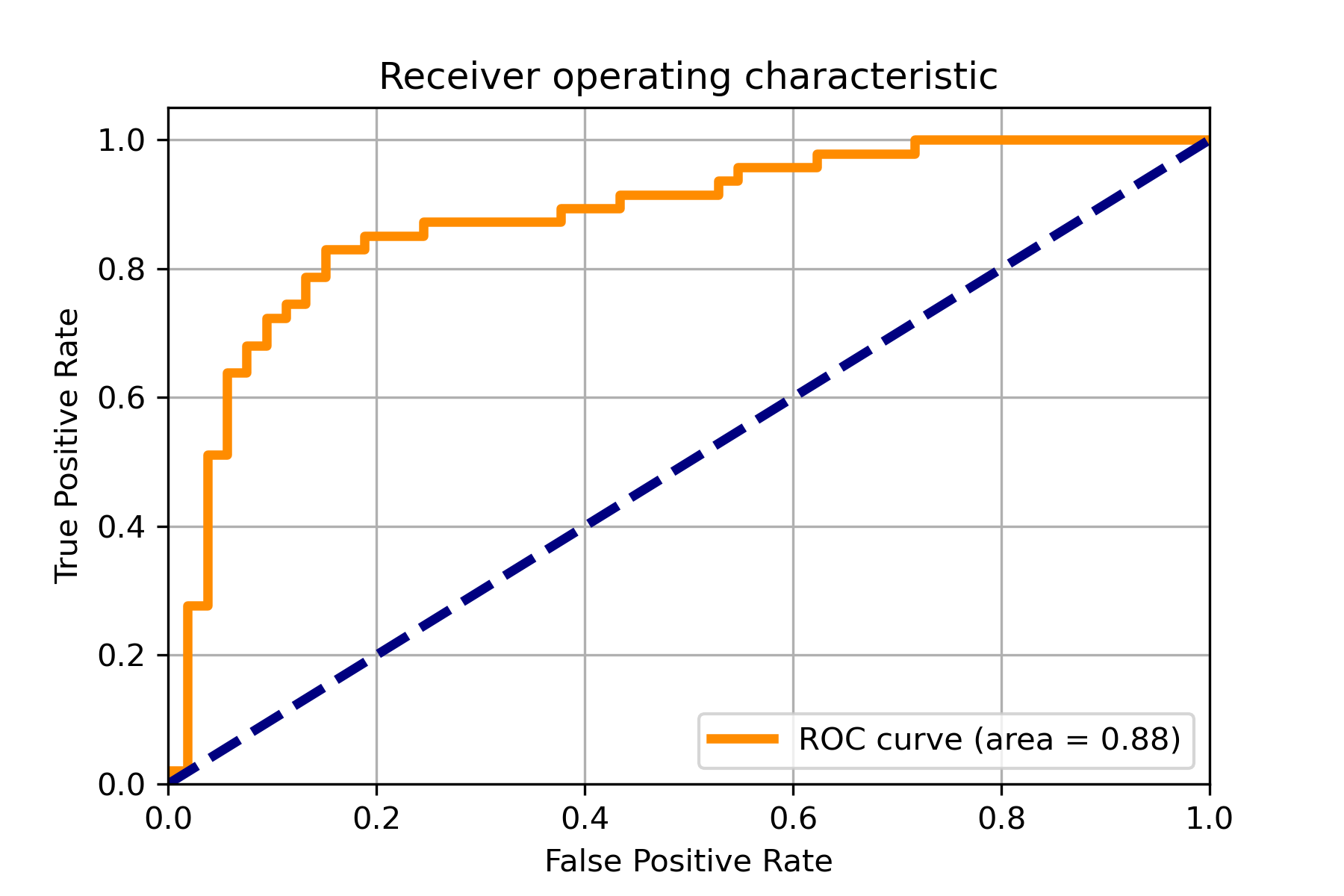
import sys sys.path.append("..") from src.BaseSVDD import BaseSVDD, BananaDataset from sko.PSO import PSO import matplotlib.pyplot as plt # Banana-shaped dataset generation and partitioning X, y = BananaDataset.generate(number=100, display='off') X_train, X_test, y_train, y_test = BananaDataset.split(X, y, ratio=0.3) # objective function def objective_func(x): x1, x2 = x svdd = BaseSVDD(C=x1, gamma=x2, kernel='rbf', display='off') y = 1-svdd.fit(X_train, y_train).accuracy return y # Do PSO pso = PSO(func=objective_func, n_dim=2, pop=10, max_iter=20, lb=[0.01, 0.01], ub=[1, 3], w=0.8, c1=0.5, c2=0.5) pso.run() print('best_x is', pso.gbest_x) print('best_y is', pso.gbest_y) # plot the result fig = plt.figure(figsize=(6, 4)) ax = fig.add_subplot(1, 1, 1) ax.plot(pso.gbest_y_hist) ax.yaxis.grid() plt.show()An example for drawing the confusion matrix and ROC curve.
An example for cross validation.
import sys sys.path.append("..") from src.BaseSVDD import BaseSVDD, BananaDataset from sklearn.model_selection import cross_val_score # Banana-shaped dataset generation and partitioning X, y = BananaDataset.generate(number=100, display='on') X_train, X_test, y_train, y_test = BananaDataset.split(X, y, ratio=0.3) # svdd = BaseSVDD(C=0.9, gamma=0.3, kernel='rbf', display='on') # cross validation (k-fold) k = 5 scores = cross_val_score(svdd, X_train, y_train, cv=k, scoring='accuracy') # print("Cross validation scores:") for scores_ in scores: print(scores_) print("Mean cross validation score: {:4f}".format(scores.mean()))Results
Cross validation scores: 0.5714285714285714 0.75 0.9642857142857143 1.0 1.0 Mean cross validation score: 0.857143 An example for parameter selection using grid search.
import sys sys.path.append("..") from sklearn.datasets import load_wine from src.BaseSVDD import BaseSVDD, BananaDataset from sklearn.model_selection import KFold, LeaveOneOut, ShuffleSplit from sklearn.model_selection import learning_curve, GridSearchCV # Banana-shaped dataset generation and partitioning X, y = BananaDataset.generate(number=100, display='off') X_train, X_test, y_train, y_test = BananaDataset.split(X, y, ratio=0.3) param_grid = [ {"kernel": ["rbf"], "gamma": [0.1, 0.2, 0.5], "C": [0.1, 0.5, 1]}, {"kernel": ["linear"], "C": [0.1, 0.5, 1]}, {"kernel": ["poly"], "C": [0.1, 0.5, 1], "degree": [2, 3, 4, 5]}, ] svdd = GridSearchCV(BaseSVDD(display='off'), param_grid, cv=5, scoring="accuracy") svdd.fit(X_train, y_train) print("best parameters:") print(svdd.best_params_) print("\n") # best_model = svdd.best_estimator_ means = svdd.cv_results_["mean_test_score"] stds = svdd.cv_results_["std_test_score"] for mean, std, params in zip(means, stds, svdd.cv_results_["params"]): print("%0.3f (+/-%0.03f) for %r" % (mean, std * 2, params)) print()Results
best parameters: {'C': 0.5, 'gamma': 0.1, 'kernel': 'rbf'} 0.921 (+/-0.159) for {'C': 0.1, 'gamma': 0.1, 'kernel': 'rbf'} 0.893 (+/-0.192) for {'C': 0.1, 'gamma': 0.2, 'kernel': 'rbf'} 0.857 (+/-0.296) for {'C': 0.1, 'gamma': 0.5, 'kernel': 'rbf'} 0.950 (+/-0.086) for {'C': 0.5, 'gamma': 0.1, 'kernel': 'rbf'} 0.921 (+/-0.131) for {'C': 0.5, 'gamma': 0.2, 'kernel': 'rbf'} 0.864 (+/-0.273) for {'C': 0.5, 'gamma': 0.5, 'kernel': 'rbf'} 0.950 (+/-0.086) for {'C': 1, 'gamma': 0.1, 'kernel': 'rbf'} 0.921 (+/-0.131) for {'C': 1, 'gamma': 0.2, 'kernel': 'rbf'} 0.864 (+/-0.273) for {'C': 1, 'gamma': 0.5, 'kernel': 'rbf'} 0.807 (+/-0.246) for {'C': 0.1, 'kernel': 'linear'} 0.821 (+/-0.278) for {'C': 0.5, 'kernel': 'linear'} 0.793 (+/-0.273) for {'C': 1, 'kernel': 'linear'} 0.879 (+/-0.184) for {'C': 0.1, 'degree': 2, 'kernel': 'poly'} 0.836 (+/-0.305) for {'C': 0.1, 'degree': 3, 'kernel': 'poly'} 0.771 (+/-0.416) for {'C': 0.1, 'degree': 4, 'kernel': 'poly'} 0.757 (+/-0.448) for {'C': 0.1, 'degree': 5, 'kernel': 'poly'} 0.871 (+/-0.224) for {'C': 0.5, 'degree': 2, 'kernel': 'poly'} 0.814 (+/-0.311) for {'C': 0.5, 'degree': 3, 'kernel': 'poly'} 0.800 (+/-0.390) for {'C': 0.5, 'degree': 4, 'kernel': 'poly'} 0.764 (+/-0.432) for {'C': 0.5, 'degree': 5, 'kernel': 'poly'} 0.871 (+/-0.224) for {'C': 1, 'degree': 2, 'kernel': 'poly'} 0.850 (+/-0.294) for {'C': 1, 'degree': 3, 'kernel': 'poly'} 0.800 (+/-0.390) for {'C': 1, 'degree': 4, 'kernel': 'poly'} 0.771 (+/-0.416) for {'C': 1, 'degree': 5, 'kernel': 'poly'}