Skip to content

Jupyter Examples

Jump to bottom
Don Jayamanne edited this page Oct 20, 2016 · 2 revisions

Examples

Standard plot

  • Paste the following code in a python file
  • Execute it (either selecting the code or using the Run cell code lens).
  • The result is a static graph displayed in the Results window
#%% import matplotlib.pyplot as plt import matplotlib as mpl import numpy as np x = np.linspace(0, 20, 100) plt.plot(x, np.sin(x)) plt.show()

Interactive Plot using D3js

  • Paste the following code in a python file
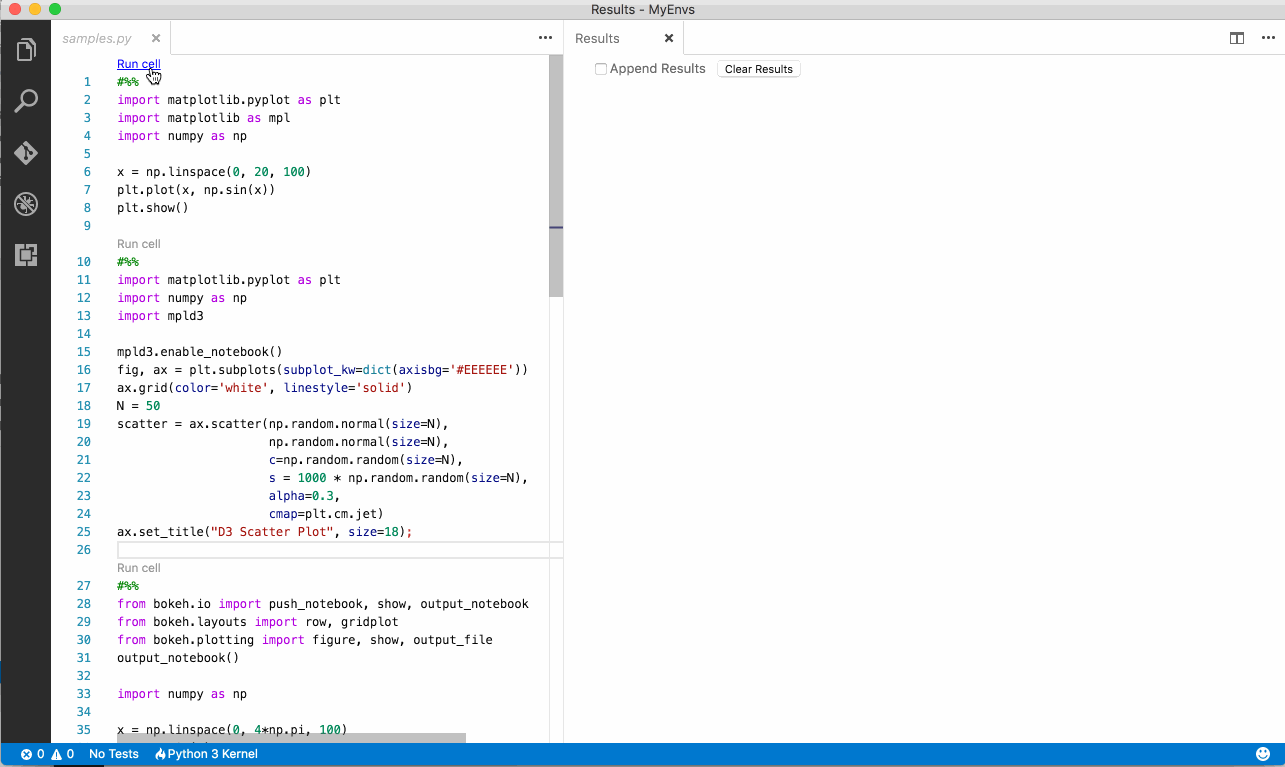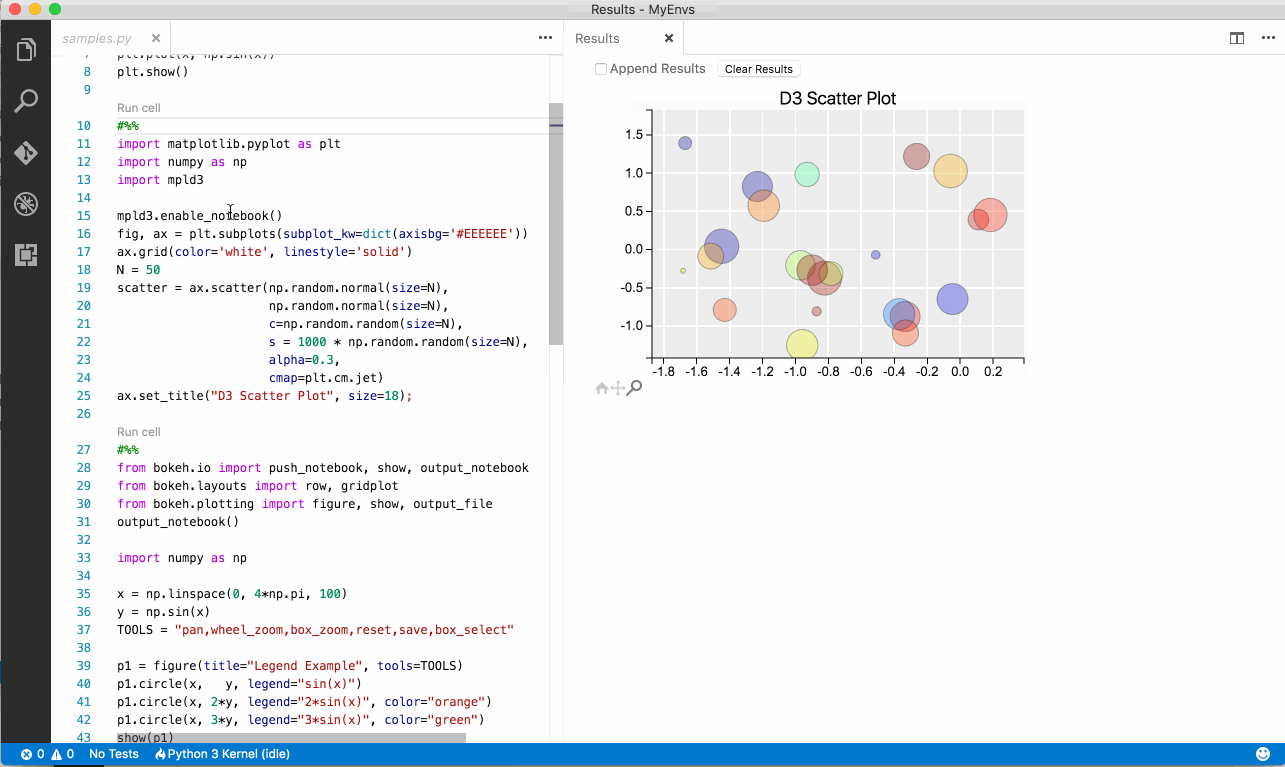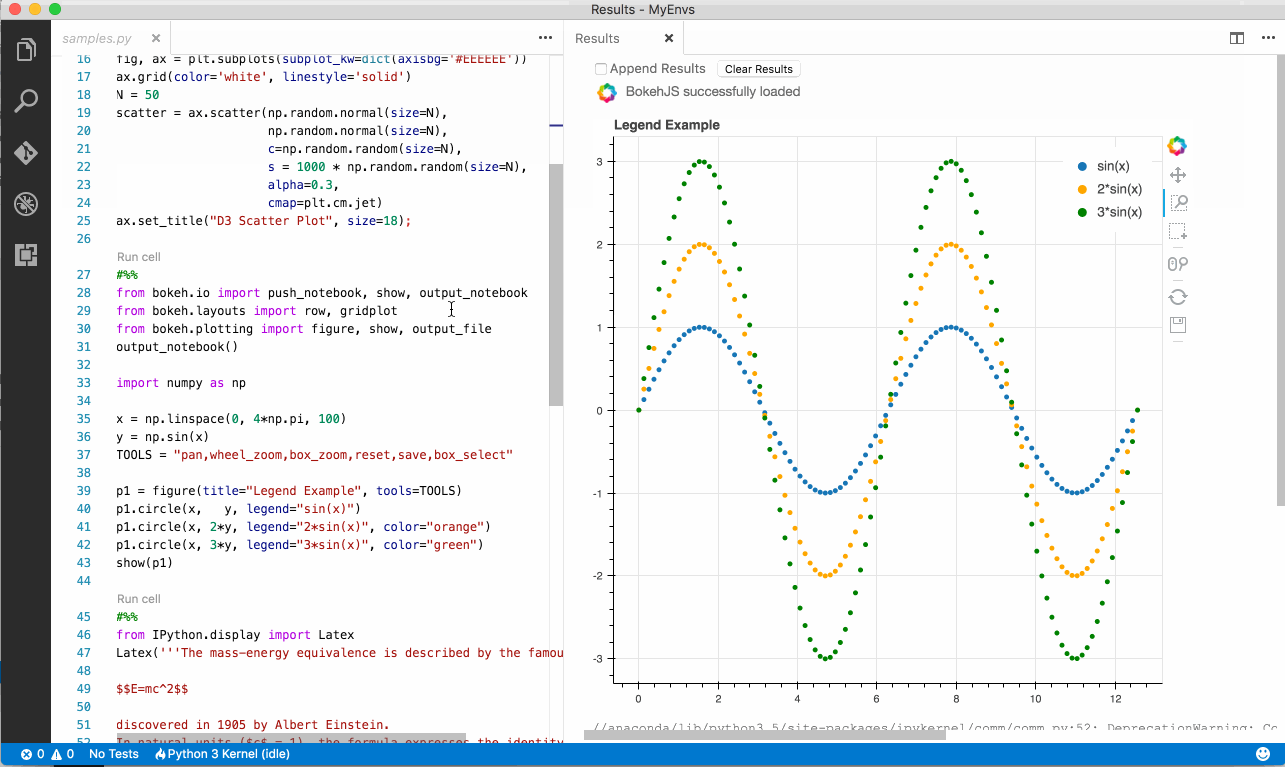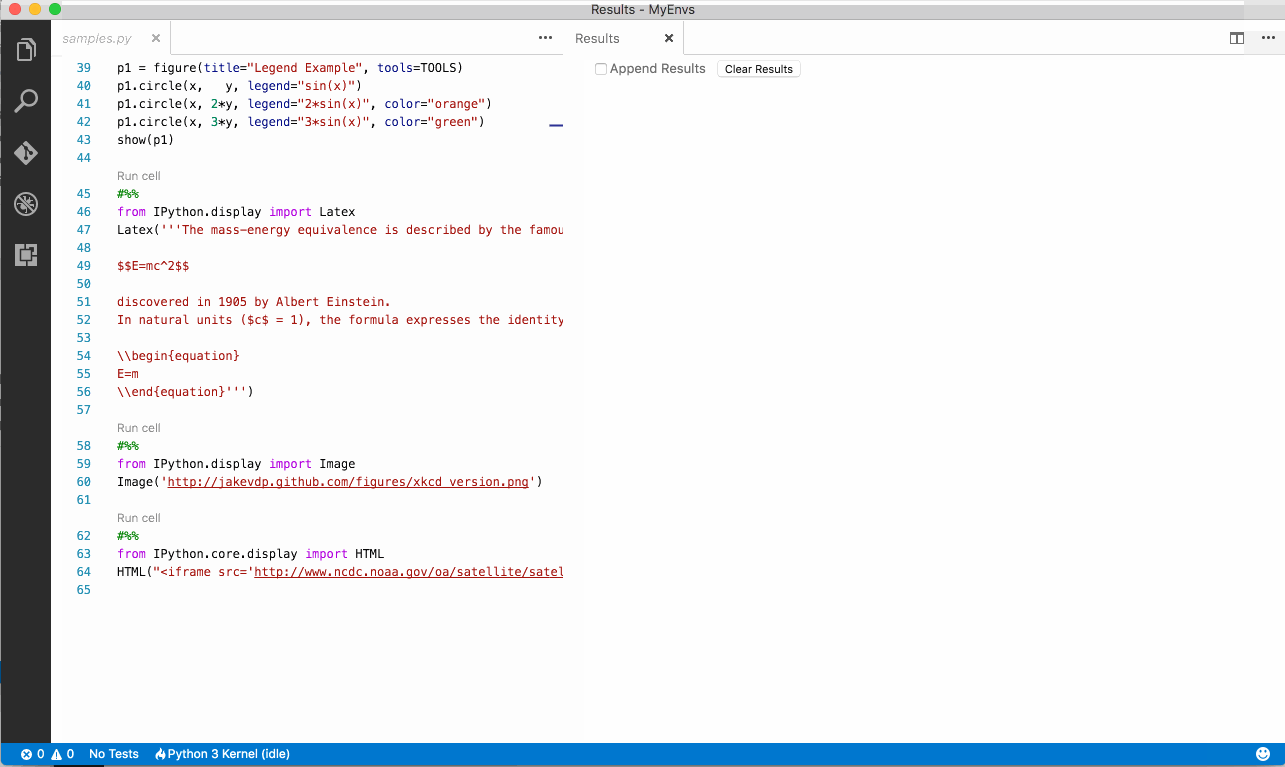
  • Execute it (either selecting the code or using the Run cell code lens).
  • The result is an interactive displayed in the Results window
  • Check here for more infor on D3js

Note: Hover the mouse over the graph and a toolbar should appear allowing you to interact with the graph

#%% import matplotlib.pyplot as plt import numpy as np import mpld3 mpld3.enable_notebook() fig, ax = plt.subplots(subplot_kw=dict(axisbg='#EEEEEE')) ax.grid(color='white', linestyle='solid') N = 50 scatter = ax.scatter(np.random.normal(size=N), np.random.normal(size=N), c=np.random.random(size=N), s = 1000 * np.random.random(size=N), alpha=0.3, cmap=plt.cm.jet) ax.set_title("D3 Scatter Plot", size=18);

Interactive Plot using Bokeh

  • Paste the following code in a python file
  • Execute it (either selecting the code or using the Run cell code lens).
  • The result is an interactive displayed in the Results window
  • Check here for more info on Bokeh graphs

Note: Use the toolbar next to the graph image, to interact with the graph.

#%% from bokeh.io import push_notebook, show, output_notebook from bokeh.layouts import row, gridplot from bokeh.plotting import figure, show, output_file output_notebook() import numpy as np x = np.linspace(0, 4*np.pi, 100) y = np.sin(x) TOOLS = "pan,wheel_zoom,box_zoom,reset,save,box_select" p1 = figure(title="Legend Example", tools=TOOLS) p1.circle(x, y, legend="sin(x)") p1.circle(x, 2*y, legend="2*sin(x)", color="orange") p1.circle(x, 3*y, legend="3*sin(x)", color="green") show(p1)

LaTex

  • Check here for more info on LaTex 
#%% from IPython.display import Latex Latex('''The mass-energy equivalence is described by the famous equation $$E=mc^2$$ discovered in 1905 by Albert Einstein. In natural units ($c$ = 1), the formula expresses the identity \\begin{equation} E=m \\end{equation}''')

Inline images

#%% from IPython.display import Image Image('http://jakevdp.github.com/figures/xkcd_version.png')

IFrame

#%% from IPython.core.display import HTML HTML("<iframe src='http://www.ncdc.noaa.gov/oa/satellite/satelliteseye/cyclones/pfctstorm91/pfctstorm.html' width='750' height='600'></iframe>")

More examples

Clone this wiki locally