27-ая задача в ЕГЭ раньше считалась самой сложной, но 23-го августа 2024 года её неплохо изменили, что именно изменили и как ее теперь решать, узнаете в этом гайде.

Задание требует внимательности, пожалуйста законспектируйте материал после прочтения.

• Есть Звезды, иначе Точки с координатами (x, y)
• Точки лежат в прямоугольниках, которые лежат на графике.
• Каждая из точек может принадлежать только в одному из k прямоугольников. Находится в нескольких одновременно они не могут
• Нужно найти точку у которой по данной нам формуле сумма расстояний до всех других точек В ОДНОМ ПРЯМОУГОЛЬНИКЕ с ней минимальна и запомнить координаты (x, y) этой точки - Такие точки называются Центроидом

• Находим все прямоугольники
• Находим все центроиды из всех прямоугольников
• Принтим или выводим в консоль в ответ в формате, который от нас требует в условие (в данном случае это среднее арифмитическое всех центроидов по x, а потом по y

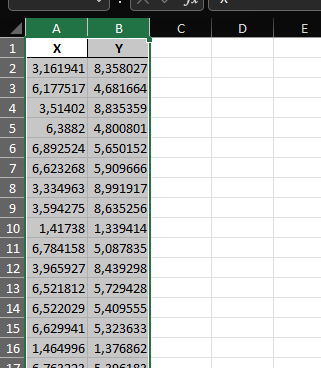
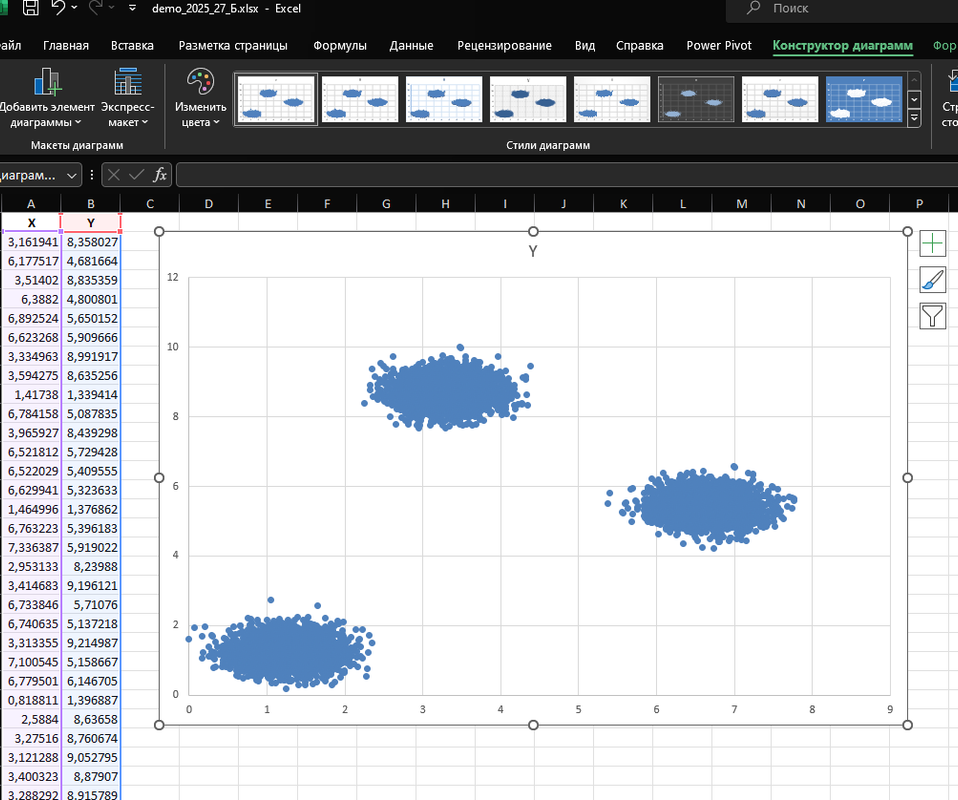
вкратце: Нам нужно построить график XoY в Экселе, либроофис, пейнте, и накинуть туда все точки

У нас есть текстовый и Эксель файлы.

Для прямоугольников нам нужно зайти в Эксель, построить диаграмму, посмотреть на неё, увидеть глазами прямоугольники, записать их границы - Вы нашли прямоугольники.

А теперь подробнее

(выделяем столбец A и B) - первые два столбца.

Нажимаем на A -> Зажимаем Shift и нажимаем на B

Нам нужна вкладка Вставка

Затем выбираем Точечную Диаграмму

Ура, мы построили Диаграмму

Как это делаю я:

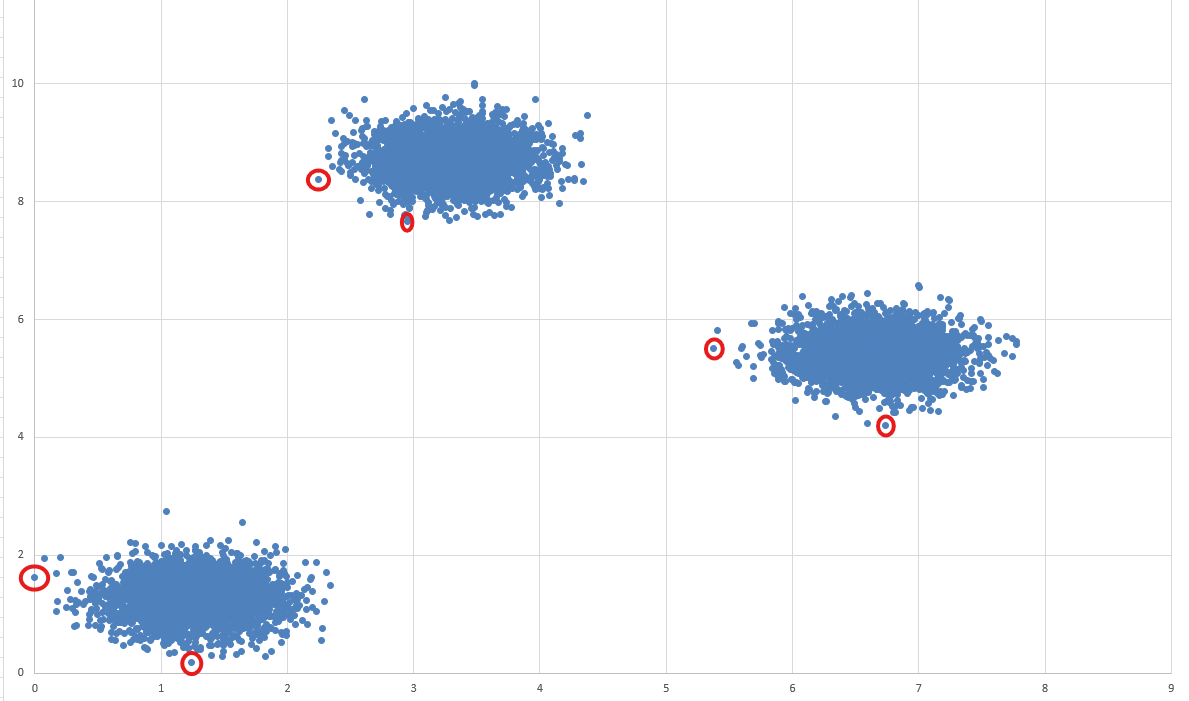
• Cмотрю на самую нижнюю точку и самую левую точку в каждом из пятен - т.е минимальные x и y в этом прямоугольнике или пятне
• Записываю сколько пятен и эти крайние значение в каждом из пятен (нижнюю и левую), можно точно, если доверяете своему глазу - пишите на глаз (у меня получилось на глаз)

Имеем:

• Левое нижнее пятно (0, 0.2~)
• Правое среднее пятно (5.3~, 4.1~)
• Левое верхнее пятно (2.3~, 7.5~)

Можно сказать мы нашли границы (координаты) прямоугольников, а т.к размеры нам уже даны в условии, мы знаем их область. Записали эти границы, закрыли эксельку или любую другу прогу с таблицами, открываем pycharm, vscode, или что у вас есть.

Напишем функцию, которая проверяет, лежит ли "какая-то" точка (x, y) в "каком-то" прямоугольнике с координатами x_min, y_min и длиной H

def is_in_cluster(x_min, y_min, x, y): return x_min <= x <= x_min + H and y_min <= y <= y_min + H

Надо пройтись по всем входным данным и сортировать эти данные в каждый из прямоугольников, буду показывать на примере самого сложного пока что варианта (Файла Б). Создадим три массива для каждого из прямоугольников и добавим в них точки, если они лежат в каком-то из прямоугольнике

N - Количество точек, в экселе последний номер строки где записаны числа - 1

 cluster_1_points = [] cluster_2_points = [] cluster_3_points = [] for _ in range(N): x, y = map(float, input().split()) if is_in_cluster(CLUSTER_1_X_MIN, CLUSTER_1_Y_MIN, x, y): cluster_1_points.append((x, y)) elif is_in_cluster(CLUSTER_2_X_MIN, CLUSTER_2_Y_MIN, x, y): cluster_2_points.append((x, y)) else: cluster_3_points.append((x, y))

Циклы, вложенные циклы, функции, и формула которую дали в условии

Надо пройтись от каждой точки по всем остальным, записывать и сранивать сумму:

Вот пример, в массиве points храним пару (x, y)

def get_centroid(points): min_sum = sys.maxsize centroid = (0, 0) for i in range(len(points)): total_distance = 0 for j in range(len(points)): total_distance += get_abs(points[i][0], points[i][1], points[j][0], points[j][1]) if total_distance < min_sum: min_sum = total_distance centroid = points[i] return centroid c_1 = get_centroid(cluster_1_points) c_2 = get_centroid(cluster_2_points) c_3 = get_centroid(cluster_3_points)

avg_x = (c_1[0] + c_2[0] + c_3[0]) / 3 avg_y = (c_1[1] + c_2[1] + c_3[1]) / 3 print(avg_x * 10000) print(avg_y * 10000)

Получаем 37522.944616 51277.958802

Не забываем записать только что просят - целую часть 37522 51277

Полные решения доступны в репозитории на C++ и Python