排序算法衍生问题
当我们掌握了冒泡排序、快速排序等基础排序算法后,会发现排序不仅仅是把数据排好序这么简单。
在实际编程和面试中,许多问题都是排序算法的变体或衍生问题。
理解这些衍生问题,能帮助我们更深刻地掌握排序算法的本质,并提升解决复杂问题的能力。
本文将探讨几个经典的排序算法衍生问题,通过分析它们的核心思想、解决方案和实际应用,帮助你建立更系统的算法思维。
什么是排序算法衍生问题?
排序算法衍生问题指的是那些不直接要求排序,但解决问题的核心思想、算法流程或数据结构与经典排序算法高度相关的问题。
这类问题通常有以下几个特点:
- 目标不同:最终目的不是输出有序序列
- 思想相通:使用排序中的比较、交换、分治等核心思想
- 复杂度相关:时间复杂度往往与排序算法在同一量级
- 应用广泛:在实际开发中经常遇到
下面我们通过几个具体问题来深入理解。
经典衍生问题一:Top K 问题
问题定义
从 n 个元素中找出最大(或最小)的 K 个元素。
实际应用场景:
- 电商网站:找出销量最高的10个商品
- 社交网络:找出粉丝最多的100个用户
- 数据分析:找出访问量最大的5个页面
解决方案对比
| 方法 | 时间复杂度 | 空间复杂度 | 适用场景 |
|---|---|---|---|
| 直接排序后取前K个 | O(n log n) | O(1) 或 O(n) | K 接近 n 时 |
| 冒泡排序 K 次 | O(n × K) | O(1) | K 非常小 (K < 10) |
| 最小堆/最大堆 | O(n log K) | O(K) | 最常用,K 远小于 n |
| 快速选择算法 | O(n) 平均,O(n²) 最坏 | O(1) | 不需要完全有序,只需Top K |
方法一:基于快速排序思想的快速选择
快速选择算法是快速排序的变体,它不需要完全排序整个数组,只需要找到第K大的元素所在的位置。
实例
def quick_select(nums, k):
"""
使用快速选择算法找到第k小的元素
nums: 输入数组
k: 要找的第k小元素 (1-based)
返回: 第k小的元素值
"""
def partition(left, right, pivot_idx):
"""分区函数,将数组分为小于和大于基准的两部分"""
pivot = nums[pivot_idx]
# 将基准移到末尾
nums[pivot_idx], nums[right] = nums[right], nums[pivot_idx]
store_idx = left
for i in range(left, right):
if nums[i] < pivot:
nums[store_idx], nums[i] = nums[i], nums[store_idx]
store_idx += 1
# 将基准移到正确位置
nums[right], nums[store_idx] = nums[store_idx], nums[right]
return store_idx
def select(left, right, k_smallest):
"""选择主函数"""
if left == right:
return nums[left]
# 随机选择基准
pivot_idx = left + (right - left) // 2
# 分区并获取基准的最终位置
pivot_idx = partition(left, right, pivot_idx)
# 基准正好是第k小的元素
if k_smallest == pivot_idx:
return nums[k_smallest]
# 第k小的元素在左半部分
elif k_smallest < pivot_idx:
return select(left, pivot_idx - 1, k_smallest)
# 第k小的元素在右半部分
else:
return select(pivot_idx + 1, right, k_smallest)
# k-1 因为内部使用0-based索引
return select(0, len(nums) - 1, k - 1)
def find_top_k(nums, k, largest=True):
"""
找到最大的k个元素
nums: 输入数组
k: 要找到的元素个数
largest: True找最大的k个,False找最小的k个
返回: 最大的k个元素列表
"""
n = len(nums)
if k >= n:
return sorted(nums, reverse=largest)
if largest:
# 找最大的k个 = 找第(n-k+1)小的元素
kth_value = quick_select(nums, n - k + 1)
# 收集所有大于等于kth_value的元素
result = [x for x in nums if x > kth_value]
# 如果数量不够,补充相等的元素
while len(result) < k:
result.append(kth_value)
return result
else:
# 找最小的k个 = 找第k小的元素
kth_value = quick_select(nums, k)
result = [x for x in nums if x < kth_value]
while len(result) < k:
result.append(kth_value)
return result
# 测试数据
test_data = [3, 2, 1, 5, 6, 4, 9, 8, 7, 0]
print("原始数据:", test_data)
print("最大的3个元素:", find_top_k(test_data.copy(), 3, largest=True))
print("最小的3个元素:", find_top_k(test_data.copy(), 3, largest=False))
"""
使用快速选择算法找到第k小的元素
nums: 输入数组
k: 要找的第k小元素 (1-based)
返回: 第k小的元素值
"""
def partition(left, right, pivot_idx):
"""分区函数,将数组分为小于和大于基准的两部分"""
pivot = nums[pivot_idx]
# 将基准移到末尾
nums[pivot_idx], nums[right] = nums[right], nums[pivot_idx]
store_idx = left
for i in range(left, right):
if nums[i] < pivot:
nums[store_idx], nums[i] = nums[i], nums[store_idx]
store_idx += 1
# 将基准移到正确位置
nums[right], nums[store_idx] = nums[store_idx], nums[right]
return store_idx
def select(left, right, k_smallest):
"""选择主函数"""
if left == right:
return nums[left]
# 随机选择基准
pivot_idx = left + (right - left) // 2
# 分区并获取基准的最终位置
pivot_idx = partition(left, right, pivot_idx)
# 基准正好是第k小的元素
if k_smallest == pivot_idx:
return nums[k_smallest]
# 第k小的元素在左半部分
elif k_smallest < pivot_idx:
return select(left, pivot_idx - 1, k_smallest)
# 第k小的元素在右半部分
else:
return select(pivot_idx + 1, right, k_smallest)
# k-1 因为内部使用0-based索引
return select(0, len(nums) - 1, k - 1)
def find_top_k(nums, k, largest=True):
"""
找到最大的k个元素
nums: 输入数组
k: 要找到的元素个数
largest: True找最大的k个,False找最小的k个
返回: 最大的k个元素列表
"""
n = len(nums)
if k >= n:
return sorted(nums, reverse=largest)
if largest:
# 找最大的k个 = 找第(n-k+1)小的元素
kth_value = quick_select(nums, n - k + 1)
# 收集所有大于等于kth_value的元素
result = [x for x in nums if x > kth_value]
# 如果数量不够,补充相等的元素
while len(result) < k:
result.append(kth_value)
return result
else:
# 找最小的k个 = 找第k小的元素
kth_value = quick_select(nums, k)
result = [x for x in nums if x < kth_value]
while len(result) < k:
result.append(kth_value)
return result
# 测试数据
test_data = [3, 2, 1, 5, 6, 4, 9, 8, 7, 0]
print("原始数据:", test_data)
print("最大的3个元素:", find_top_k(test_data.copy(), 3, largest=True))
print("最小的3个元素:", find_top_k(test_data.copy(), 3, largest=False))
方法二:基于堆排序的解决方案
堆是解决Top K问题的经典数据结构,特别适合处理数据流场景。
实例
import heapq
def find_top_k_with_heap(nums, k, largest=True):
"""
使用堆找到最大的k个元素
nums: 输入数组
k: 要找到的元素个数
largest: True找最大的k个,False找最小的k个
返回: 最大的k个元素列表
"""
if largest:
# 找最大的k个:使用最小堆
heap = []
for num in nums:
if len(heap) < k:
heapq.heappush(heap, num)
elif num > heap[0]: # 当前元素比堆顶大
heapq.heapreplace(heap, num)
return sorted(heap, reverse=True)
else:
# 找最小的k个:使用最大堆(通过取负数实现)
heap = []
for num in nums:
if len(heap) < k:
heapq.heappush(heap, -num) # 存负数
elif num < -heap[0]: # 当前元素比堆顶小
heapq.heapreplace(heap, -num)
return sorted([-x for x in heap])
# 测试堆方法
print("\n使用堆方法:")
print("最大的3个元素:", find_top_k_with_heap(test_data, 3, largest=True))
print("最小的3个元素:", find_top_k_with_heap(test_data, 3, largest=False))
def find_top_k_with_heap(nums, k, largest=True):
"""
使用堆找到最大的k个元素
nums: 输入数组
k: 要找到的元素个数
largest: True找最大的k个,False找最小的k个
返回: 最大的k个元素列表
"""
if largest:
# 找最大的k个:使用最小堆
heap = []
for num in nums:
if len(heap) < k:
heapq.heappush(heap, num)
elif num > heap[0]: # 当前元素比堆顶大
heapq.heapreplace(heap, num)
return sorted(heap, reverse=True)
else:
# 找最小的k个:使用最大堆(通过取负数实现)
heap = []
for num in nums:
if len(heap) < k:
heapq.heappush(heap, -num) # 存负数
elif num < -heap[0]: # 当前元素比堆顶小
heapq.heapreplace(heap, -num)
return sorted([-x for x in heap])
# 测试堆方法
print("\n使用堆方法:")
print("最大的3个元素:", find_top_k_with_heap(test_data, 3, largest=True))
print("最小的3个元素:", find_top_k_with_heap(test_data, 3, largest=False))
经典衍生问题二:逆序对计数
问题定义
在一个数组中,如果前面的元素大于后面的元素,则这两个元素构成一个逆序对。计算数组中逆序对的总数。
实际应用场景:
- 衡量数据的有序程度
- 推荐系统中的用户偏好分析
- 版本控制系统中的修改冲突检测
解决方案:基于归并排序的算法
归并排序的过程中天然地可以统计逆序对数量,这是分治思想的典型应用。
实例
def count_inversions(nums):
"""
计算数组中的逆序对数量
使用基于归并排序的方法
"""
def merge_sort_count(left, right):
"""归并排序并统计逆序对"""
if left >= right:
return 0, [nums[left]] if left == right else []
mid = (left + right) // 2
# 递归统计左右两部分的逆序对
left_count, left_arr = merge_sort_count(left, mid)
right_count, right_arr = merge_sort_count(mid + 1, right)
# 统计跨越中点的逆序对
cross_count = 0
merged = []
i = j = 0
while i < len(left_arr) and j < len(right_arr):
if left_arr[i] <= right_arr[j]:
merged.append(left_arr[i])
i += 1
else:
# left_arr[i] > right_arr[j],构成逆序对
merged.append(right_arr[j])
cross_count += len(left_arr) - i # 关键:左边剩余元素都与right_arr[j]构成逆序对
j += 1
# 添加剩余元素
merged.extend(left_arr[i:])
merged.extend(right_arr[j:])
total_count = left_count + right_count + cross_count
return total_count, merged
if not nums:
return 0
count, _ = merge_sort_count(0, len(nums) - 1)
return count
# 测试逆序对计数
test_cases = [
([1, 2, 3, 4, 5], 0), # 完全有序,逆序对为0
([5, 4, 3, 2, 1], 10), # 完全逆序,逆序对为C(5,2)=10
([2, 4, 1, 3, 5], 3), # 示例
([7, 5, 6, 4], 5), # 复杂示例
]
print("\n逆序对计数测试:")
for nums, expected in test_cases:
result = count_inversions(nums.copy())
print(f"数组 {nums}: 计算值={result}, 期望值={expected}, {'正确' if result == expected else '错误'}")
"""
计算数组中的逆序对数量
使用基于归并排序的方法
"""
def merge_sort_count(left, right):
"""归并排序并统计逆序对"""
if left >= right:
return 0, [nums[left]] if left == right else []
mid = (left + right) // 2
# 递归统计左右两部分的逆序对
left_count, left_arr = merge_sort_count(left, mid)
right_count, right_arr = merge_sort_count(mid + 1, right)
# 统计跨越中点的逆序对
cross_count = 0
merged = []
i = j = 0
while i < len(left_arr) and j < len(right_arr):
if left_arr[i] <= right_arr[j]:
merged.append(left_arr[i])
i += 1
else:
# left_arr[i] > right_arr[j],构成逆序对
merged.append(right_arr[j])
cross_count += len(left_arr) - i # 关键:左边剩余元素都与right_arr[j]构成逆序对
j += 1
# 添加剩余元素
merged.extend(left_arr[i:])
merged.extend(right_arr[j:])
total_count = left_count + right_count + cross_count
return total_count, merged
if not nums:
return 0
count, _ = merge_sort_count(0, len(nums) - 1)
return count
# 测试逆序对计数
test_cases = [
([1, 2, 3, 4, 5], 0), # 完全有序,逆序对为0
([5, 4, 3, 2, 1], 10), # 完全逆序,逆序对为C(5,2)=10
([2, 4, 1, 3, 5], 3), # 示例
([7, 5, 6, 4], 5), # 复杂示例
]
print("\n逆序对计数测试:")
for nums, expected in test_cases:
result = count_inversions(nums.copy())
print(f"数组 {nums}: 计算值={result}, 期望值={expected}, {'正确' if result == expected else '错误'}")
下图展示了归并排序过程中如何统计逆序对。关键点在于:当右半部分的元素小于左半部分的某个元素时,左半部分剩余的所有元素都与该右半部分元素构成逆序对。
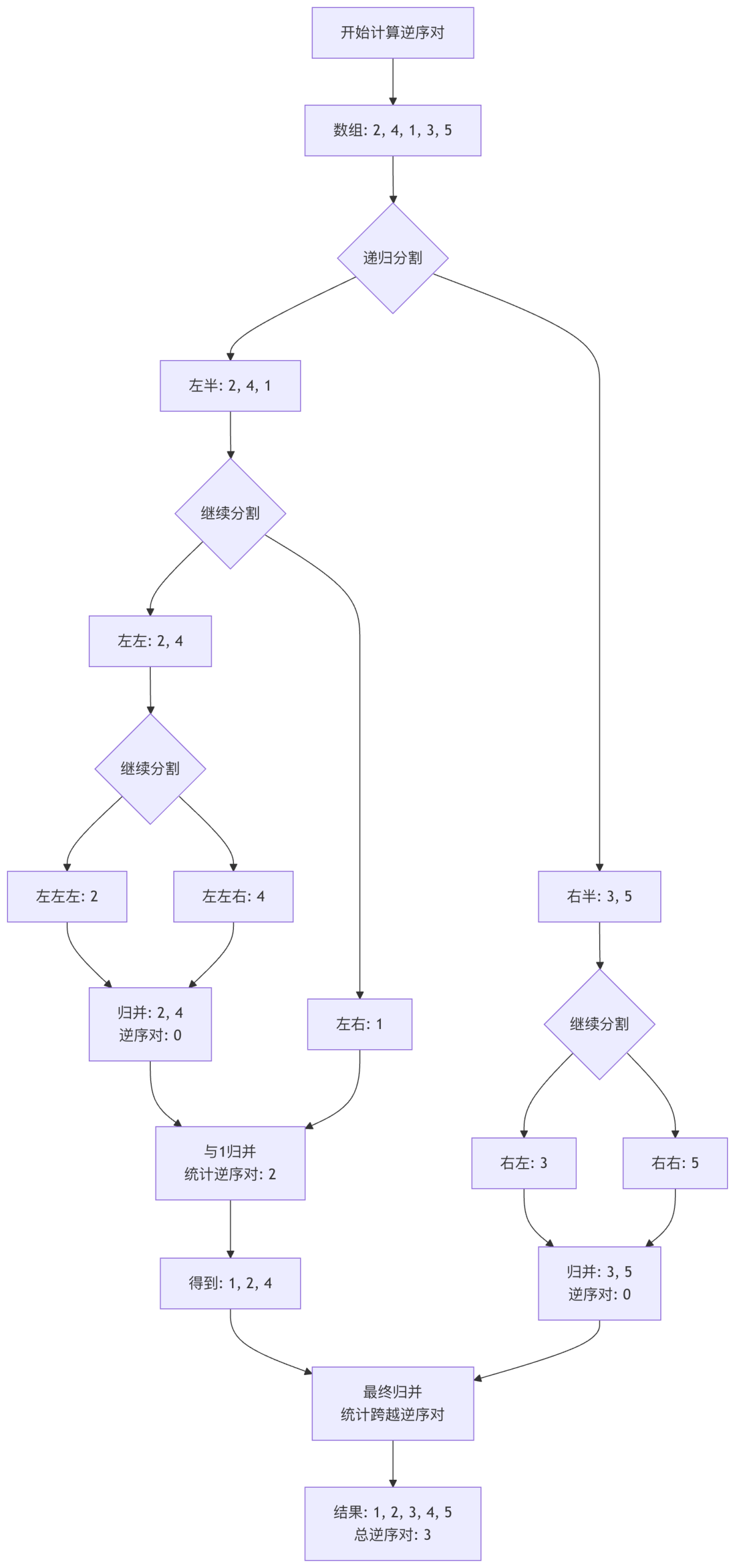
经典衍生问题三:第K大/第K小元素
这个问题是Top K问题的特例,但解法更加多样。
多种解法对比
| 方法 | 时间复杂度 | 空间复杂度 | 特点 |
|---|---|---|---|
| 排序后直接取 | O(n log n) | O(1) 或 O(n) | 最简单直观 |
| 快速选择 | O(n) 平均 | O(1) | 最优平均复杂度 |
| 堆方法 | O(n log k) | O(k) | 适合数据流 |
| 计数排序 | O(n + m) | O(m) | 适合数据范围小的情况 |
完整实现示例
实例
def find_kth_smallest(nums, k):
"""找到第k小的元素(1-based)"""
# 方法1: 直接排序
def method_sort():
return sorted(nums)[k-1]
# 方法2: 快速选择(上面已实现)
def method_quick_select():
return quick_select(nums.copy(), k)
# 方法3: 堆方法
def method_heap():
# 使用最大堆找第k小
heap = []
for num in nums:
if len(heap) < k:
heapq.heappush(heap, -num) # 最大堆通过负数实现
elif num < -heap[0]:
heapq.heapreplace(heap, -num)
return -heap[0]
# 方法4: 计数排序(适合数据范围小的情况)
def method_counting():
if not nums:
return None
# 找出数据范围
min_val, max_val = min(nums), max(nums)
range_size = max_val - min_val + 1
# 计数
count = [0] * range_size
for num in nums:
count[num - min_val] += 1
# 找到第k小
accumulated = 0
for i in range(range_size):
accumulated += count[i]
if accumulated >= k:
return i + min_val
return None
# 验证所有方法结果一致
result1 = method_sort()
result2 = method_quick_select()
result3 = method_heap()
result4 = method_counting()
print(f"\n第{k}小元素查找测试(数组: {nums}):")
print(f"排序法: {result1}")
print(f"快速选择: {result2}")
print(f"堆方法: {result3}")
print(f"计数法: {result4}")
# 验证一致性
assert result1 == result2 == result3 == result4, "不同方法结果不一致!"
return result1
# 测试数据
test_nums = [3, 2, 3, 1, 2, 4, 5, 5, 6]
for k in [1, 3, 5, 7]:
find_kth_smallest(test_nums.copy(), k)
"""找到第k小的元素(1-based)"""
# 方法1: 直接排序
def method_sort():
return sorted(nums)[k-1]
# 方法2: 快速选择(上面已实现)
def method_quick_select():
return quick_select(nums.copy(), k)
# 方法3: 堆方法
def method_heap():
# 使用最大堆找第k小
heap = []
for num in nums:
if len(heap) < k:
heapq.heappush(heap, -num) # 最大堆通过负数实现
elif num < -heap[0]:
heapq.heapreplace(heap, -num)
return -heap[0]
# 方法4: 计数排序(适合数据范围小的情况)
def method_counting():
if not nums:
return None
# 找出数据范围
min_val, max_val = min(nums), max(nums)
range_size = max_val - min_val + 1
# 计数
count = [0] * range_size
for num in nums:
count[num - min_val] += 1
# 找到第k小
accumulated = 0
for i in range(range_size):
accumulated += count[i]
if accumulated >= k:
return i + min_val
return None
# 验证所有方法结果一致
result1 = method_sort()
result2 = method_quick_select()
result3 = method_heap()
result4 = method_counting()
print(f"\n第{k}小元素查找测试(数组: {nums}):")
print(f"排序法: {result1}")
print(f"快速选择: {result2}")
print(f"堆方法: {result3}")
print(f"计数法: {result4}")
# 验证一致性
assert result1 == result2 == result3 == result4, "不同方法结果不一致!"
return result1
# 测试数据
test_nums = [3, 2, 3, 1, 2, 4, 5, 5, 6]
for k in [1, 3, 5, 7]:
find_kth_smallest(test_nums.copy(), k)
经典衍生问题四:区间合并
问题定义
给定一组区间,合并所有重叠的区间。
实际应用场景:
- 日历应用中的时间段合并
- 项目管理中的任务时间安排
- 网络IP地址段的合并
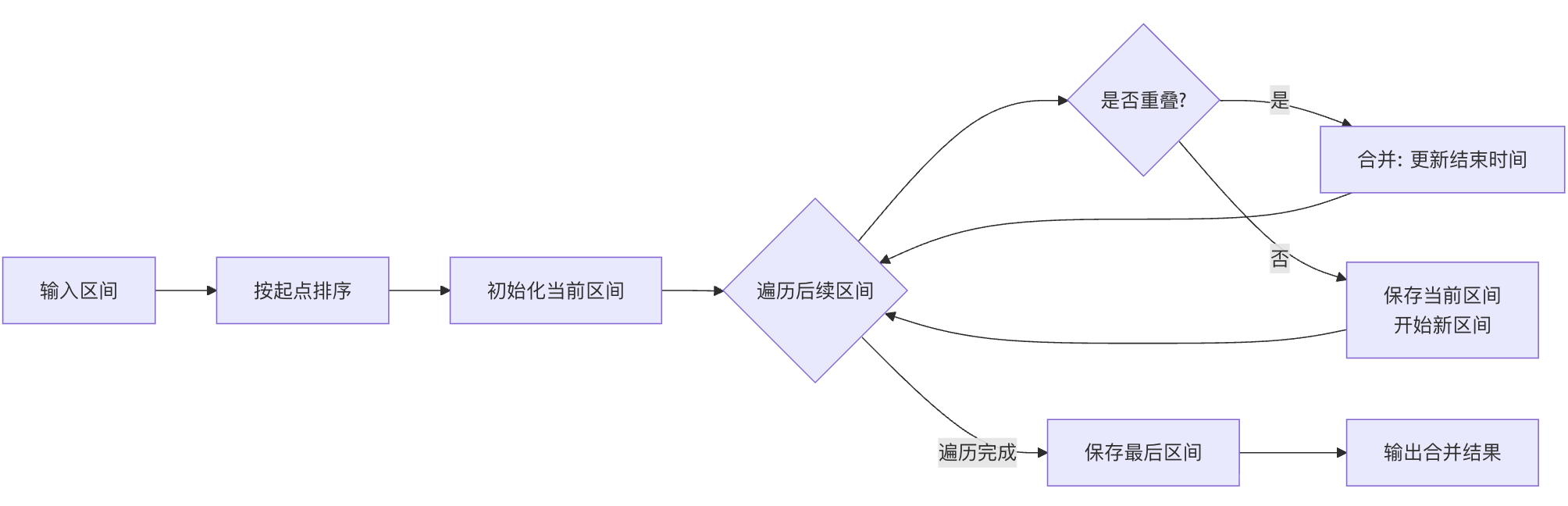
解决方案:排序+线性扫描
实例
def merge_intervals(intervals):
"""
合并重叠的区间
intervals: 列表的列表,每个子列表表示一个区间 [start, end]
返回: 合并后的区间列表
"""
if not intervals:
return []
# 关键步骤1: 按区间起点排序
intervals.sort(key=lambda x: x[0])
merged = []
# 关键步骤2: 线性扫描合并
current_start, current_end = intervals[0]
for interval in intervals[1:]:
start, end = interval
if start <= current_end: # 有重叠
# 合并区间:取最大的结束点
current_end = max(current_end, end)
else: # 无重叠
# 保存当前区间
merged.append([current_start, current_end])
# 开始新的区间
current_start, current_end = start, end
# 添加最后一个区间
merged.append([current_start, current_end])
return merged
# 测试区间合并
test_intervals = [
[[1, 3], [2, 6], [8, 10], [15, 18]],
[[1, 4], [4, 5]],
[[1, 4], [0, 4]],
[[1, 4], [2, 3]], # 完全包含
[[1, 4], [0, 2], [3, 5]], # 复杂情况
]
print("\n区间合并测试:")
for i, intervals in enumerate(test_intervals, 1):
result = merge_intervals(intervals.copy())
print(f"测试用例 {i}:")
print(f" 输入: {intervals}")
print(f" 输出: {result}")
print()
"""
合并重叠的区间
intervals: 列表的列表,每个子列表表示一个区间 [start, end]
返回: 合并后的区间列表
"""
if not intervals:
return []
# 关键步骤1: 按区间起点排序
intervals.sort(key=lambda x: x[0])
merged = []
# 关键步骤2: 线性扫描合并
current_start, current_end = intervals[0]
for interval in intervals[1:]:
start, end = interval
if start <= current_end: # 有重叠
# 合并区间:取最大的结束点
current_end = max(current_end, end)
else: # 无重叠
# 保存当前区间
merged.append([current_start, current_end])
# 开始新的区间
current_start, current_end = start, end
# 添加最后一个区间
merged.append([current_start, current_end])
return merged
# 测试区间合并
test_intervals = [
[[1, 3], [2, 6], [8, 10], [15, 18]],
[[1, 4], [4, 5]],
[[1, 4], [0, 4]],
[[1, 4], [2, 3]], # 完全包含
[[1, 4], [0, 2], [3, 5]], # 复杂情况
]
print("\n区间合并测试:")
for i, intervals in enumerate(test_intervals, 1):
result = merge_intervals(intervals.copy())
print(f"测试用例 {i}:")
print(f" 输入: {intervals}")
print(f" 输出: {result}")
print()
算法过程解析
实践练习
现在,让我们通过几个练习来巩固所学知识:
练习1:颜色分类(荷兰国旗问题)
给定一个包含红色、白色和蓝色,一共 n 个元素的数组,原地对它们进行排序,使得相同颜色的元素相邻,并按照红色、白色、蓝色的顺序排列。
实例
def sort_colors(nums):
"""
原地排序颜色数组
0: 红色, 1: 白色, 2: 蓝色
使用三指针法(类似快速排序的分区思想)
"""
# 初始化三个指针
left = 0 # 红色区域的右边界
current = 0 # 当前检查的元素
right = len(nums) - 1 # 蓝色区域的左边界
while current <= right:
if nums[current] == 0: # 红色
nums[left], nums[current] = nums[current], nums[left]
left += 1
current += 1
elif nums[current] == 1: # 白色
current += 1
else: # 蓝色
nums[current], nums[right] = nums[right], nums[current]
right -= 1
# 注意:这里不增加current,因为交换过来的元素还没检查
return nums
# 测试
colors = [2, 0, 2, 1, 1, 0]
print("颜色排序前:", colors)
print("颜色排序后:", sort_colors(colors.copy()))
"""
原地排序颜色数组
0: 红色, 1: 白色, 2: 蓝色
使用三指针法(类似快速排序的分区思想)
"""
# 初始化三个指针
left = 0 # 红色区域的右边界
current = 0 # 当前检查的元素
right = len(nums) - 1 # 蓝色区域的左边界
while current <= right:
if nums[current] == 0: # 红色
nums[left], nums[current] = nums[current], nums[left]
left += 1
current += 1
elif nums[current] == 1: # 白色
current += 1
else: # 蓝色
nums[current], nums[right] = nums[right], nums[current]
right -= 1
# 注意:这里不增加current,因为交换过来的元素还没检查
return nums
# 测试
colors = [2, 0, 2, 1, 1, 0]
print("颜色排序前:", colors)
print("颜色排序后:", sort_colors(colors.copy()))
练习2:数组中的第K个最大元素
在未排序的数组中找到第 k 个最大的元素。
实例
def find_kth_largest(nums, k):
"""
找到第k大的元素
使用快速选择算法
"""
# 第k大 = 第(n-k+1)小
k_smallest = len(nums) - k + 1
def quick_select(arr, left, right, k_small):
if left == right:
return arr[left]
# 选择基准
pivot_idx = (left + right) // 2
pivot = arr[pivot_idx]
# 分区
arr[pivot_idx], arr[right] = arr[right], arr[pivot_idx]
store_idx = left
for i in range(left, right):
if arr[i] < pivot:
arr[store_idx], arr[i] = arr[i], arr[store_idx]
store_idx += 1
arr[right], arr[store_idx] = arr[store_idx], arr[right]
# 递归选择
if k_small == store_idx:
return arr[store_idx]
elif k_small < store_idx:
return quick_select(arr, left, store_idx - 1, k_small)
else:
return quick_select(arr, store_idx + 1, right, k_small)
return quick_select(nums.copy(), 0, len(nums) - 1, k_smallest - 1)
# 测试
test_array = [3, 2, 1, 5, 6, 4]
k = 2
print(f"\n数组 {test_array} 中第 {k} 大的元素是: {find_kth_largest(test_array, k)}")
"""
找到第k大的元素
使用快速选择算法
"""
# 第k大 = 第(n-k+1)小
k_smallest = len(nums) - k + 1
def quick_select(arr, left, right, k_small):
if left == right:
return arr[left]
# 选择基准
pivot_idx = (left + right) // 2
pivot = arr[pivot_idx]
# 分区
arr[pivot_idx], arr[right] = arr[right], arr[pivot_idx]
store_idx = left
for i in range(left, right):
if arr[i] < pivot:
arr[store_idx], arr[i] = arr[i], arr[store_idx]
store_idx += 1
arr[right], arr[store_idx] = arr[store_idx], arr[right]
# 递归选择
if k_small == store_idx:
return arr[store_idx]
elif k_small < store_idx:
return quick_select(arr, left, store_idx - 1, k_small)
else:
return quick_select(arr, store_idx + 1, right, k_small)
return quick_select(nums.copy(), 0, len(nums) - 1, k_smallest - 1)
# 测试
test_array = [3, 2, 1, 5, 6, 4]
k = 2
print(f"\n数组 {test_array} 中第 {k} 大的元素是: {find_kth_largest(test_array, k)}")

点我分享笔记