Given a subset $\mathcal S\subset \mathbb N\setminus\{0\}$ of (strictly) positive integers, we can consider subsets $A$ of $\mathbb N$ (or $\mathbb Z$) with no differences in $\mathcal S$.
Examples: If $\mathcal S=1+2\mathbb N$ we can take $A=2\mathbb N$. If $\mathcal S=(2n)^{\mathbb N}=\lbrace 1,2n,(2n)^2,\ldots\rbrace$, we can take for $\mathcal A$ all integers in the classes of $0,2,4,\ldots,2n-2 \pmod{2n+1}$.
If $\mathcal S=\mathcal F=\lbrace 1,2,3,5,8,13,21,34,\ldots\rbrace$ is the set of Fibonacci numbers, the greedy algorithm (which adds iteratively the smallest possible element) starting with $0$ yields $$A=\lbrace 0,4,10,14,20,24,30,36,40,46,50,56,60,66,72,76,82,\ldots\rbrace \ .$$ (This sequence is missing in the OEIS, the sequence augmented by $1$ coincides with A314043 up to $56+1=57$ before differing by $1$ on $60+1=61<62$.)
Denoting by $a_1=0<a_2=4<a_3=10<\ldots$ the increasing sequence underlying $\mathcal A$, the graph of the function $i\longmapsto \frac{a_i}{i}$ for $i=400,\ldots,12000$ is given by
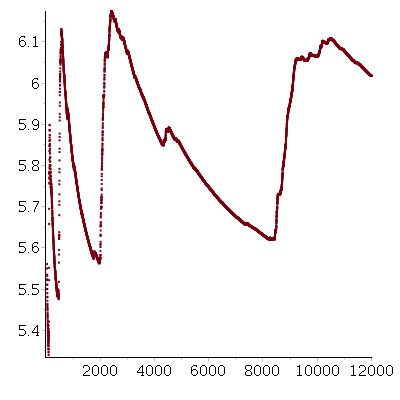$i\longmapsto \frac{a_i}{i},i=400\ldots 12000$" />
This suggests perhaps the existence of a limit-density of $\mathcal A$ as a subset of $\mathbb N$.
Multiplicities in gap-sizes of the increasing sequence $a_1,a_2,\ldots$ define the gap-size polynomial $G(N)=\sum_{i=1}^{N-1}t^{a_{i+1}-a_i}$. We get $$G(1000)=354t^4+553t^6+8t^7+9t^9+42t^{10}+t^{11}+11t^{12}+t^{14} +2t^{15}+9t^{16}+\ldots+t^{28}$$ and $$G(10000)=3445t^4+5467t^6+40t^7+57t^9+498t^{10}+10t^{11}+121t^{12}+\ldots+t^{54}$$ indicating perhaps also some sort of limit frequencies for gap-sizes.
A final observation is the rarity of odd elements in $\mathcal A$: only 97 of the first $10000$ elements in $\mathcal A$ are odd. (For $n$ an odd number, elements of $A$ seem to be more ore less equidistributed modulo $n$.)
Is there an explanation for these (empirical) observations or are they artefacts?
