If we look at the difference between the number of partitions of $n$ with distinct parts that have an even number of parts and the number of partitions of $n$ with distinct parts that have an odd number of parts we get Euler's pentagonal theorem. What happens when we look at the difference between the number of partitions of $n$ with parts differing by at least 2 that have an even number of parts and the number of partitions of $n$ parts differing by at least 2 that have an odd number of parts. Is this difference limited some way? Is it ever bigger in absolute value than one? Are there known upper or lower bounds as n goes to infinity?
$\begingroup$ $\endgroup$
2 - 1$\begingroup$ It is 2 for $n=8$ :) $\endgroup$მამუკა ჯიბლაძე– მამუკა ჯიბლაძე2016-03-15 18:53:09 +00:00Commented Mar 15, 2016 at 18:53
- 1$\begingroup$ Related: Rogers' Theorem, at en.wikipedia.org/wiki/Glaisher%27s_theorem $\endgroup$Gerry Myerson– Gerry Myerson2016-03-15 22:06:18 +00:00Commented Mar 15, 2016 at 22:06
Add a comment |
1 Answer
$\begingroup$ $\endgroup$
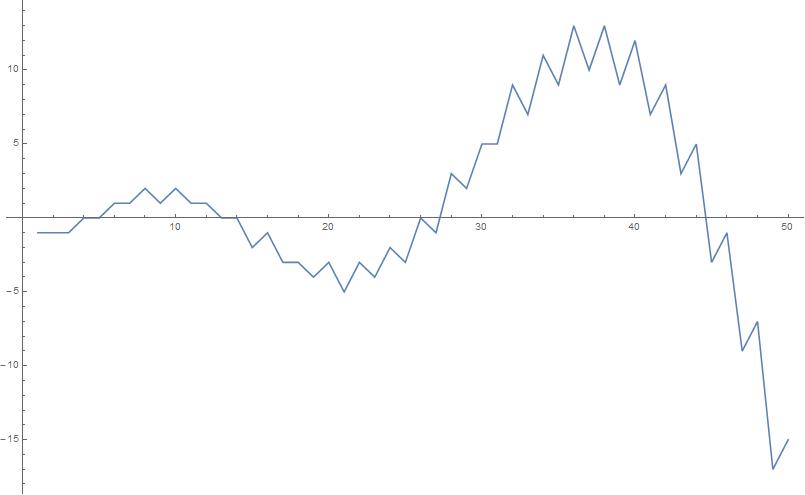
4 The graph certainly looks promising :)
As for the generating function - what I managed to get is a very strange "downside-up continued fraction" $$ 1-q-q^2\frac{1-q^2-q^4\frac{1-q^3-q^6 \frac{1-q^4-q^8\frac{ 1-q^5-q^{10}\frac{1-q^6-q^{12}\cdots}{1-q^5}}{1-q^4}}{1-q^3}}{1-q^2}}{1-q} $$ Looks like it is A039924, in which case this generating function is equal to $$ 1-\frac q{1-q}+\frac{q^4}{(1-q) \left(1-q^2\right)}-\frac{q^9}{(1-q) \left(1-q^2\right) \left(1-q^3\right)}+...$$
- $\begingroup$ I assume this is a graph of the difference in question. How was it computed? Could it be extended further or are there computational obstacles preventing this after 50. It raises some more questions: Does this graph ever stabilize at one sign? Is its increase or decrease as n goes to n+1 limited by some integer? What is that integer if it exists? Can you show the absolute value exceeds any integer? $\endgroup$Kristal Cantwell– Kristal Cantwell2016-03-15 19:07:42 +00:00Commented Mar 15, 2016 at 19:07
- $\begingroup$ I used quick and dirty Mathematica code
ListPlot[Table[With[{l = Select[IntegerPartitions[n], Max[Differences[#]] < -1 &]}, 2Length[Select[l, EvenQ@*Length]] - Length[l]], {n, 50}], Joined -> True], surely it can be done much better $\endgroup$მამუკა ჯიბლაძე– მამუკა ჯიბლაძე2016-03-15 21:58:23 +00:00Commented Mar 15, 2016 at 21:58 - $\begingroup$ @KristalCantwell Thanks for accepting but this does not really answer any of your questions :D So I will leave it cw I think... $\endgroup$მამუკა ჯიბლაძე– მამუკა ჯიბლაძე2016-03-17 06:32:43 +00:00Commented Mar 17, 2016 at 6:32
- $\begingroup$ It was useful especially the link to A039924. $\endgroup$Kristal Cantwell– Kristal Cantwell2016-03-17 17:00:48 +00:00Commented Mar 17, 2016 at 17:00