- Notifications
You must be signed in to change notification settings - Fork 97
Added tasks 1766, 1769, 1770, 1771, 1773 #786
New issue
Have a question about this project? Sign up for a free GitHub account to open an issue and contact its maintainers and the community.
By clicking “Sign up for GitHub”, you agree to our terms of service and privacy statement. We’ll occasionally send you account related emails.
Already on GitHub? Sign in to your account
Merged
javadev merged 3 commits into javadev:main from ThanhNIT:tasks-1766-1769-1770-1771-1773 Apr 30, 2022
Merged
Changes from 2 commits
Commits
Show all changes
3 commits Select commit Hold shift + click to select a range
File filter
Filter by extension
Conversations
Failed to load comments.
Loading
Jump to
Jump to file
Failed to load files.
Loading
Diff view
Diff view
There are no files selected for viewing
72 changes: 72 additions & 0 deletions 72 src/main/java/g1701_1800/s1766_tree_of_coprimes/Solution.java
This file contains hidden or bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters. Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,72 @@ | ||
| package g1701_1800.s1766_tree_of_coprimes; | ||
| | ||
| // #Hard #Math #Depth_First_Search #Breadth_First_Search #Tree | ||
| // #2022_04_30_Time_111_ms_(94.07%)_Space_155.4_MB_(40.68%) | ||
| | ||
| import java.util.ArrayList; | ||
| import java.util.Arrays; | ||
| | ||
| public class Solution { | ||
| private void dfs( | ||
| int[] v2n, | ||
| int[] v2d, | ||
| int depth, | ||
| int parent, | ||
| int node, | ||
| int[] ans, | ||
| int[] nums, | ||
| ArrayList<Integer>[] neighbors) { | ||
| | ||
| int d = Integer.MIN_VALUE; | ||
| int n = -1; | ||
| | ||
| int v = nums[node]; | ||
| for (int i = 1; i <= 50; i++) { | ||
| if (v2n[i] != -1 && v2d[i] > d && gcd(i, v) == 1) { | ||
| d = v2d[i]; | ||
| n = v2n[i]; | ||
| } | ||
| } | ||
| ans[node] = n; | ||
| | ||
| int v2NOld = v2n[v]; | ||
| int v2DOld = v2d[v]; | ||
| | ||
| v2n[v] = node; | ||
| v2d[v] = depth; | ||
| for (int child : neighbors[node]) { | ||
| if (child == parent) { | ||
| continue; | ||
| } | ||
| dfs(v2n, v2d, depth + 1, node, child, ans, nums, neighbors); | ||
| } | ||
| | ||
| v2n[v] = v2NOld; | ||
| v2d[v] = v2DOld; | ||
| } | ||
| | ||
| private int gcd(int x, int y) { | ||
| return x == 0 ? y : gcd(y % x, x); | ||
| } | ||
| | ||
| public int[] getCoprimes(int[] nums, int[][] edges) { | ||
| | ||
| int n = nums.length; | ||
| | ||
| ArrayList<Integer>[] neighbors = new ArrayList[n]; | ||
| for (int i = 0; i < n; i++) { | ||
| neighbors[i] = new ArrayList<>(); | ||
| } | ||
| for (int[] edge : edges) { | ||
| neighbors[edge[0]].add(edge[1]); | ||
| neighbors[edge[1]].add(edge[0]); | ||
| } | ||
| | ||
| int[] ans = new int[n]; | ||
| int[] v2n = new int[51]; | ||
| int[] v2d = new int[51]; | ||
| Arrays.fill(v2n, -1); | ||
| dfs(v2n, v2d, 0, -1, 0, ans, nums, neighbors); | ||
| return ans; | ||
| } | ||
| } | ||
This file contains hidden or bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters. Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,47 @@ | ||
| 1766\. Tree of Coprimes | ||
| | ||
| Hard | ||
| | ||
| There is a tree (i.e., a connected, undirected graph that has no cycles) consisting of `n` nodes numbered from `0` to `n - 1` and exactly `n - 1` edges. Each node has a value associated with it, and the **root** of the tree is node `0`. | ||
| | ||
| To represent this tree, you are given an integer array `nums` and a 2D array `edges`. Each `nums[i]` represents the <code>i<sup>th</sup></code> node's value, and each <code>edges[j] = [u<sub>j</sub>, v<sub>j</sub>]</code> represents an edge between nodes <code>u<sub>j</sub></code> and <code>v<sub>j</sub></code> in the tree. | ||
| | ||
| Two values `x` and `y` are **coprime** if `gcd(x, y) == 1` where `gcd(x, y)` is the **greatest common divisor** of `x` and `y`. | ||
| | ||
| An ancestor of a node `i` is any other node on the shortest path from node `i` to the **root**. A node is **not** considered an ancestor of itself. | ||
| | ||
| Return _an array_ `ans` _of size_ `n`, _where_ `ans[i]` _is the closest ancestor to node_ `i` _such that_ `nums[i]` _and_ `nums[ans[i]]` are **coprime**, or `-1` _if there is no such ancestor_. | ||
| | ||
| **Example 1:** | ||
| | ||
| **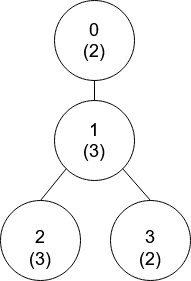** | ||
| | ||
| **Input:** nums = [2,3,3,2], edges = [[0,1],[1,2],[1,3]] | ||
| | ||
| **Output:** [-1,0,0,1] | ||
| | ||
| **Explanation:** In the above figure, each node's value is in parentheses. | ||
| | ||
| - Node 0 has no coprime ancestors. | ||
| | ||
| - Node 1 has only one ancestor, node 0. Their values are coprime (gcd(2,3) == 1). - Node 2 has two ancestors, nodes 1 and 0. Node 1's value is not coprime (gcd(3,3) == 3), but node 0's value is (gcd(2,3) == 1), so node 0 is the closest valid ancestor. | ||
| | ||
| - Node 3 has two ancestors, nodes 1 and 0. It is coprime with node 1 (gcd(3,2) == 1), so node 1 is its closest valid ancestor. | ||
| | ||
| **Example 2:** | ||
| | ||
| 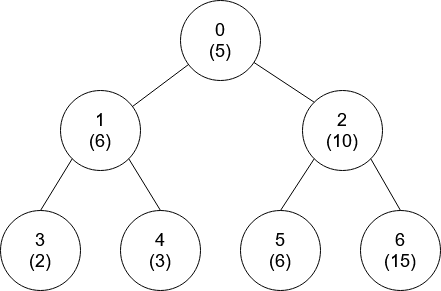 | ||
| | ||
| **Input:** nums = [5,6,10,2,3,6,15], edges = [[0,1],[0,2],[1,3],[1,4],[2,5],[2,6]] | ||
| | ||
| **Output:** [-1,0,-1,0,0,0,-1] | ||
| | ||
| **Constraints:** | ||
| | ||
| * `nums.length == n` | ||
| * `1 <= nums[i] <= 50` | ||
| * <code>1 <= n <= 10<sup>5</sup></code> | ||
| * `edges.length == n - 1` | ||
| * `edges[j].length == 2` | ||
| * <code>0 <= u<sub>j</sub>, v<sub>j</sub> < n</code> | ||
| * <code>u<sub>j</sub> != v<sub>j</sub></code> |
35 changes: 35 additions & 0 deletions 35 ...g1701_1800/s1769_minimum_number_of_operations_to_move_all_balls_to_each_box/Solution.java
This file contains hidden or bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters. Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,35 @@ | ||
| package g1701_1800.s1769_minimum_number_of_operations_to_move_all_balls_to_each_box; | ||
| | ||
| // #Medium #Array #String #2022_04_30_Time_3_ms_(91.66%)_Space_47.8_MB_(35.95%) | ||
| | ||
| public class Solution { | ||
| public int[] minOperations(String boxes) { | ||
| | ||
| int countFromLeft = 0; | ||
| int countFromRight = 0; | ||
| int moves = 0; | ||
| int[] result = new int[boxes.length()]; | ||
| | ||
| for (char c : boxes.toCharArray()) { | ||
| moves += countFromLeft; | ||
| if (c == '1') { | ||
| countFromLeft++; | ||
| } | ||
| } | ||
| | ||
| for (int i = boxes.length() - 1; i >= 0; i--) { | ||
| char c = boxes.charAt(i); | ||
| result[i] = moves; | ||
| | ||
| if (c == '1') { | ||
| countFromLeft--; | ||
| countFromRight++; | ||
| } | ||
| | ||
| ||
| moves -= countFromLeft; | ||
| moves += countFromRight; | ||
| } | ||
| | ||
| return result; | ||
| } | ||
| } | ||
37 changes: 37 additions & 0 deletions 37 ...1800/s1769_minimum_number_of_operations_to_move_all_balls_to_each_box/readme.md
This file contains hidden or bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters. Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,37 @@ | ||
| 1769\. Minimum Number of Operations to Move All Balls to Each Box | ||
| | ||
| Medium | ||
| | ||
| You have `n` boxes. You are given a binary string `boxes` of length `n`, where `boxes[i]` is `'0'` if the <code>i<sup>th</sup></code> box is **empty**, and `'1'` if it contains **one** ball. | ||
| | ||
| In one operation, you can move **one** ball from a box to an adjacent box. Box `i` is adjacent to box `j` if `abs(i - j) == 1`. Note that after doing so, there may be more than one ball in some boxes. | ||
| | ||
| Return an array `answer` of size `n`, where `answer[i]` is the **minimum** number of operations needed to move all the balls to the <code>i<sup>th</sup></code> box. | ||
| | ||
| Each `answer[i]` is calculated considering the **initial** state of the boxes. | ||
| | ||
| **Example 1:** | ||
| | ||
| **Input:** boxes = "110" | ||
| | ||
| **Output:** [1,1,3] | ||
| | ||
| **Explanation:** The answer for each box is as follows: | ||
| | ||
| 1) First box: you will have to move one ball from the second box to the first box in one operation. | ||
| | ||
| 2) Second box: you will have to move one ball from the first box to the second box in one operation. | ||
| | ||
| 3) Third box: you will have to move one ball from the first box to the third box in two operations, and move one ball from the second box to the third box in one operation. | ||
| | ||
| **Example 2:** | ||
| | ||
| **Input:** boxes = "001011" | ||
| | ||
| **Output:** [11,8,5,4,3,4] | ||
| | ||
| **Constraints:** | ||
| | ||
| * `n == boxes.length` | ||
| * `1 <= n <= 2000` | ||
| * `boxes[i]` is either `'0'` or `'1'`. |
27 changes: 27 additions & 0 deletions 27 ...va/g1701_1800/s1770_maximum_score_from_performing_multiplication_operations/Solution.java
This file contains hidden or bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters. Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,27 @@ | ||
| package g1701_1800.s1770_maximum_score_from_performing_multiplication_operations; | ||
| | ||
| // #Medium #Array #Dynamic_Programming #2022_04_30_Time_31_ms_(92.41%)_Space_53.2_MB_(88.74%) | ||
| | ||
| public class Solution { | ||
| | ||
| public int maximumScore(int[] nums, int[] mult) { | ||
| int n = nums.length; | ||
| int m = mult.length; | ||
| int row = m; | ||
| int[] dp = new int[m]; | ||
| int[] prev = new int[m + 1]; | ||
| | ||
| while (--row >= 0) { | ||
| for (int i = 0; i <= row; ++i) { | ||
| dp[i] = | ||
| Math.max( | ||
| prev[i] + mult[row] * nums[n - row + i - 1], | ||
| prev[i + 1] + mult[row] * nums[i]); | ||
| } | ||
| | ||
| ||
| prev = dp; | ||
| } | ||
| | ||
| return dp[0]; | ||
| } | ||
| } | ||
57 changes: 57 additions & 0 deletions 57 ...01_1800/s1770_maximum_score_from_performing_multiplication_operations/readme.md
This file contains hidden or bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters. Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,57 @@ | ||
| 1770\. Maximum Score from Performing Multiplication Operations | ||
| | ||
| Medium | ||
| | ||
| You are given two integer arrays `nums` and `multipliers` of size `n` and `m` respectively, where `n >= m`. The arrays are **1-indexed**. | ||
| | ||
| You begin with a score of `0`. You want to perform **exactly** `m` operations. On the <code>i<sup>th</sup></code> operation **(1-indexed)**, you will: | ||
| | ||
| * Choose one integer `x` from **either the start or the end** of the array `nums`. | ||
| * Add `multipliers[i] * x` to your score. | ||
| * Remove `x` from the array `nums`. | ||
| | ||
| Return _the **maximum** score after performing_ `m` _operations._ | ||
| | ||
| **Example 1:** | ||
| | ||
| **Input:** nums = [1,2,3], multipliers = [3,2,1] | ||
| | ||
| **Output:** 14 | ||
| | ||
| **Explanation:** An optimal solution is as follows: | ||
| | ||
| - Choose from the end, [1,2,**3**], adding 3 \* 3 = 9 to the score. | ||
| | ||
| - Choose from the end, [1,**2**], adding 2 \* 2 = 4 to the score. | ||
| | ||
| - Choose from the end, [**1**], adding 1 \* 1 = 1 to the score. | ||
| | ||
| The total score is 9 + 4 + 1 = 14. | ||
| | ||
| **Example 2:** | ||
| | ||
| **Input:** nums = [-5,-3,-3,-2,7,1], multipliers = [-10,-5,3,4,6] | ||
| | ||
| **Output:** 102 | ||
| | ||
| **Explanation:** An optimal solution is as follows: | ||
| | ||
| - Choose from the start, [**\-5**,-3,-3,-2,7,1], adding -5 \* -10 = 50 to the score. | ||
| | ||
| - Choose from the start, [**\-3**,-3,-2,7,1], adding -3 \* -5 = 15 to the score. | ||
| | ||
| - Choose from the start, [**\-3**,-2,7,1], adding -3 \* 3 = -9 to the score. | ||
| | ||
| - Choose from the end, [-2,7,**1**], adding 1 \* 4 = 4 to the score. | ||
| | ||
| - Choose from the end, [-2,**7**], adding 7 \* 6 = 42 to the score. | ||
| | ||
| The total score is 50 + 15 - 9 + 4 + 42 = 102. | ||
| | ||
| **Constraints:** | ||
| | ||
| * `n == nums.length` | ||
| * `m == multipliers.length` | ||
| * <code>1 <= m <= 10<sup>3</sup></code> | ||
| * <code>m <= n <= 10<sup>5</sup></code> | ||
| * `-1000 <= nums[i], multipliers[i] <= 1000` |
29 changes: 29 additions & 0 deletions 29 src/main/java/g1701_1800/s1771_maximize_palindrome_length_from_subsequences/Solution.java
This file contains hidden or bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters. Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,29 @@ | ||
| package g1701_1800.s1771_maximize_palindrome_length_from_subsequences; | ||
| | ||
| // #Hard #String #Dynamic_Programming #2022_04_30_Time_58_ms_(87.88%)_Space_67.1_MB_(92.42%) | ||
| | ||
| public class Solution { | ||
| public int longestPalindrome(String word1, String word2) { | ||
| int len1 = word1.length(); | ||
| int len2 = word2.length(); | ||
| int len = len1 + len2; | ||
| String word = word1 + word2; | ||
| int[][] dp = new int[len][len]; | ||
| int max = 0; | ||
| char[] arr = word.toCharArray(); | ||
| for (int d = 1; d <= len; d++) { | ||
| for (int i = 0; i + d - 1 < len; i++) { | ||
| if (arr[i] == arr[i + d - 1]) { | ||
| dp[i][i + d - 1] = | ||
| d == 1 ? 1 : Math.max(dp[i + 1][i + d - 2] + 2, dp[i][i + d - 1]); | ||
| if (i < len1 && i + d - 1 >= len1) { | ||
| max = Math.max(max, dp[i][i + d - 1]); | ||
| } | ||
| } else { | ||
| dp[i][i + d - 1] = Math.max(dp[i + 1][i + d - 1], dp[i][i + d - 2]); | ||
| } | ||
| } | ||
| } | ||
| return max; | ||
| } | ||
| } |
44 changes: 44 additions & 0 deletions 44 ...in/java/g1701_1800/s1771_maximize_palindrome_length_from_subsequences/readme.md
This file contains hidden or bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters. Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,44 @@ | ||
| 1771\. Maximize Palindrome Length From Subsequences | ||
| | ||
| Hard | ||
| | ||
| You are given two strings, `word1` and `word2`. You want to construct a string in the following manner: | ||
| | ||
| * Choose some **non-empty** subsequence `subsequence1` from `word1`. | ||
| * Choose some **non-empty** subsequence `subsequence2` from `word2`. | ||
| * Concatenate the subsequences: `subsequence1 + subsequence2`, to make the string. | ||
| | ||
| Return _the **length** of the longest **palindrome** that can be constructed in the described manner._ If no palindromes can be constructed, return `0`. | ||
| | ||
| A **subsequence** of a string `s` is a string that can be made by deleting some (possibly none) characters from `s` without changing the order of the remaining characters. | ||
| | ||
| A **palindrome** is a string that reads the same forward as well as backward. | ||
| | ||
| **Example 1:** | ||
| | ||
| **Input:** word1 = "cacb", word2 = "cbba" | ||
| | ||
| **Output:** 5 | ||
| | ||
| **Explanation:** Choose "ab" from word1 and "cba" from word2 to make "abcba", which is a palindrome. | ||
| | ||
| **Example 2:** | ||
| | ||
| **Input:** word1 = "ab", word2 = "ab" | ||
| | ||
| **Output:** 3 | ||
| | ||
| **Explanation:** Choose "ab" from word1 and "a" from word2 to make "aba", which is a palindrome. | ||
| | ||
| **Example 3:** | ||
| | ||
| **Input:** word1 = "aa", word2 = "bb" | ||
| | ||
| **Output:** 0 | ||
| | ||
| **Explanation:** You cannot construct a palindrome from the described method, so return 0. | ||
| | ||
| **Constraints:** | ||
| | ||
| * `1 <= word1.length, word2.length <= 1000` | ||
| * `word1` and `word2` consist of lowercase English letters. |
19 changes: 19 additions & 0 deletions 19 src/main/java/g1701_1800/s1773_count_items_matching_a_rule/Solution.java
This file contains hidden or bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters. Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,19 @@ | ||
| package g1701_1800.s1773_count_items_matching_a_rule; | ||
| | ||
| // #Easy #Array #String #2022_04_30_Time_7_ms_(25.91%)_Space_56.9_MB_(35.49%) | ||
| | ||
| import java.util.List; | ||
| | ||
| public class Solution { | ||
| public int countMatches(List<List<String>> items, String ruleKey, String ruleValue) { | ||
| int match = 0; | ||
| for (List<String> item : items) { | ||
| if ((ruleKey.equals("type") && item.get(0).equals(ruleValue)) | ||
| || (ruleKey.equals("color") && item.get(1).equals(ruleValue)) | ||
| || (ruleKey.equals("name") && item.get(2).equals(ruleValue))) { | ||
| match++; | ||
| } | ||
| } | ||
| return match; | ||
| } | ||
| } |
Oops, something went wrong.
Add this suggestion to a batch that can be applied as a single commit. This suggestion is invalid because no changes were made to the code. Suggestions cannot be applied while the pull request is closed. Suggestions cannot be applied while viewing a subset of changes. Only one suggestion per line can be applied in a batch. Add this suggestion to a batch that can be applied as a single commit. Applying suggestions on deleted lines is not supported. You must change the existing code in this line in order to create a valid suggestion. Outdated suggestions cannot be applied. This suggestion has been applied or marked resolved. Suggestions cannot be applied from pending reviews. Suggestions cannot be applied on multi-line comments. Suggestions cannot be applied while the pull request is queued to merge. Suggestion cannot be applied right now. Please check back later.
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
Please remove empty lines.