- Notifications
You must be signed in to change notification settings - Fork 97
Added tasks 2869-2873 #1634
New issue
Have a question about this project? Sign up for a free GitHub account to open an issue and contact its maintainers and the community.
By clicking “Sign up for GitHub”, you agree to our terms of service and privacy statement. We’ll occasionally send you account related emails.
Already on GitHub? Sign in to your account
Merged
Merged
Added tasks 2869-2873 #1634
Changes from 2 commits
Commits
Show all changes
10 commits Select commit Hold shift + click to select a range
f37046a Added tasks 2869-2873
ThanhNIT fb6c099 Update Solution.java
ThanhNIT 7252261 Update Solution.java
ThanhNIT 722e56d Update Solution.java
ThanhNIT b0d98c0 Update Solution.java
ThanhNIT 53d8b24 Update Solution.java
javadev 578e787 Update Solution.java
javadev d0ac4b7 Update SolutionTest.java
javadev 2b859e4 Update SolutionTest.java
javadev f39503f Update SolutionTest.java
javadev File filter
Filter by extension
Conversations
Failed to load comments.
Loading
Jump to
Jump to file
Failed to load files.
Loading
Diff view
Diff view
There are no files selected for viewing
38 changes: 38 additions & 0 deletions 38 src/main/java/g2801_2900/s2869_minimum_operations_to_collect_elements/Solution.java
This file contains hidden or bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters. Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,38 @@ | ||
| package g2801_2900.s2869_minimum_operations_to_collect_elements; | ||
| | ||
| // #Easy #Array #Hash_Table #2023_12_21_Time_1_ms_(100.00%)_Space_42.4_MB_(5.72%) | ||
| | ||
| import java.util.List; | ||
| | ||
| public class Solution { | ||
| public int minOperations(List<Integer> nums, int k) { | ||
| Pair[] visited = new Pair[k + 1]; | ||
| visited[0] = new Pair(true, 0); | ||
| int count = 0; | ||
| for (int i = nums.size() - 1; i >= 0; i--) { | ||
| count++; | ||
| if (nums.get(i) <= k && visited[nums.get(i)] == null) { | ||
| visited[nums.get(i)] = new Pair(true, count); | ||
| } | ||
| } | ||
| int fin = -1; | ||
| for (Pair pair : visited) { | ||
| if (pair != null && !pair.isVisited) { | ||
| return -1; | ||
| } else if (pair != null) { | ||
| fin = Math.max(fin, pair.totalVisitedTillNow); | ||
| } | ||
| } | ||
| return fin; | ||
| } | ||
| | ||
| static class Pair { | ||
| boolean isVisited; | ||
| int totalVisitedTillNow; | ||
| | ||
| public Pair(boolean isVisited, int totalVisitedTillNow) { | ||
| this.isVisited = isVisited; | ||
| this.totalVisitedTillNow = totalVisitedTillNow; | ||
| } | ||
| } | ||
| } |
40 changes: 40 additions & 0 deletions 40 src/main/java/g2801_2900/s2869_minimum_operations_to_collect_elements/readme.md
This file contains hidden or bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters. Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,40 @@ | ||
| 2869\. Minimum Operations to Collect Elements | ||
| | ||
| Easy | ||
| | ||
| You are given an array `nums` of positive integers and an integer `k`. | ||
| | ||
| In one operation, you can remove the last element of the array and add it to your collection. | ||
| | ||
| Return _the **minimum number of operations** needed to collect elements_ `1, 2, ..., k`. | ||
| | ||
| **Example 1:** | ||
| | ||
| **Input:** nums = [3,1,5,4,2], k = 2 | ||
| | ||
| **Output:** 4 | ||
| | ||
| **Explanation:** After 4 operations, we collect elements 2, 4, 5, and 1, in this order. Our collection contains elements 1 and 2. Hence, the answer is 4. | ||
| | ||
| **Example 2:** | ||
| | ||
| **Input:** nums = [3,1,5,4,2], k = 5 | ||
| | ||
| **Output:** 5 | ||
| | ||
| **Explanation:** After 5 operations, we collect elements 2, 4, 5, 1, and 3, in this order. Our collection contains elements 1 through 5. Hence, the answer is 5. | ||
| | ||
| **Example 3:** | ||
| | ||
| **Input:** nums = [3,2,5,3,1], k = 3 | ||
| | ||
| **Output:** 4 | ||
| | ||
| **Explanation:** After 4 operations, we collect elements 1, 3, 5, and 2, in this order. Our collection contains elements 1 through 3. Hence, the answer is 4. | ||
| | ||
| **Constraints:** | ||
| | ||
| * `1 <= nums.length <= 50` | ||
| * `1 <= nums[i] <= nums.length` | ||
| * `1 <= k <= nums.length` | ||
| * The input is generated such that you can collect elements `1, 2, ..., k`. |
29 changes: 29 additions & 0 deletions 29 ...main/java/g2801_2900/s2870_minimum_number_of_operations_to_make_array_empty/Solution.java
This file contains hidden or bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters. Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,29 @@ | ||
| package g2801_2900.s2870_minimum_number_of_operations_to_make_array_empty; | ||
| | ||
| // #Medium #Array #Hash_Table #Greedy #Counting | ||
| // #2023_12_21_Time_6_ms_(98.16%)_Space_58.3_MB_(14.76%) | ||
| | ||
| import java.util.Arrays; | ||
| | ||
| public class Solution { | ||
| public int minOperations(int[] nums) { | ||
| Arrays.sort(nums); | ||
| int count; | ||
| int min = 0; | ||
| int current; | ||
| for (int i = 0; i < nums.length; i++) { | ||
| current = nums[i]; | ||
| count = 0; | ||
| while (i < nums.length && current == nums[i]) { | ||
| count += 1; | ||
| i++; | ||
| } | ||
| if (count == 1) { | ||
| return -1; | ||
| } | ||
| min += Math.ceil(count / (3 * 1.0)); | ||
| ||
| i--; | ||
| } | ||
| return min; | ||
| } | ||
| } | ||
39 changes: 39 additions & 0 deletions 39 ...ava/g2801_2900/s2870_minimum_number_of_operations_to_make_array_empty/readme.md
This file contains hidden or bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters. Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,39 @@ | ||
| 2870\. Minimum Number of Operations to Make Array Empty | ||
| | ||
| Medium | ||
| | ||
| You are given a **0-indexed** array `nums` consisting of positive integers. | ||
| | ||
| There are two types of operations that you can apply on the array **any** number of times: | ||
| | ||
| * Choose **two** elements with **equal** values and **delete** them from the array. | ||
| * Choose **three** elements with **equal** values and **delete** them from the array. | ||
| | ||
| Return _the **minimum** number of operations required to make the array empty, or_ `-1` _if it is not possible_. | ||
| | ||
| **Example 1:** | ||
| | ||
| **Input:** nums = [2,3,3,2,2,4,2,3,4] | ||
| | ||
| **Output:** 4 | ||
| | ||
| **Explanation:** We can apply the following operations to make the array empty: | ||
| - Apply the first operation on the elements at indices 0 and 3. The resulting array is nums = [3,3,2,4,2,3,4]. | ||
| - Apply the first operation on the elements at indices 2 and 4. The resulting array is nums = [3,3,4,3,4]. | ||
| - Apply the second operation on the elements at indices 0, 1, and 3. The resulting array is nums = [4,4]. | ||
| - Apply the first operation on the elements at indices 0 and 1. The resulting array is nums = []. | ||
| | ||
| It can be shown that we cannot make the array empty in less than 4 operations. | ||
| | ||
| **Example 2:** | ||
| | ||
| **Input:** nums = [2,1,2,2,3,3] | ||
| | ||
| **Output:** -1 | ||
| | ||
| **Explanation:** It is impossible to empty the array. | ||
| | ||
| **Constraints:** | ||
| | ||
| * <code>2 <= nums.length <= 10<sup>5</sup></code> | ||
| * <code>1 <= nums[i] <= 10<sup>6</sup></code> |
32 changes: 32 additions & 0 deletions 32 src/main/java/g2801_2900/s2871_split_array_into_maximum_number_of_subarrays/Solution.java
This file contains hidden or bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters. Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,32 @@ | ||
| package g2801_2900.s2871_split_array_into_maximum_number_of_subarrays; | ||
| | ||
| // #Medium #Array #Greedy #Bit_Manipulation #2023_12_21_Time_3_ms_(100.00%)_Space_59.7_MB_(5.43%) | ||
| | ||
| public class Solution { | ||
| public int maxSubarrays(int[] nums) { | ||
| if (nums.length == 1) { | ||
| return 1; | ||
| } | ||
| int andMax = nums[0]; | ||
| int count = 0; | ||
| int currAnd = nums[0]; | ||
| int sum = 0; | ||
| for (int n : nums) { | ||
| andMax &= n; | ||
| } | ||
| for (int i = 1; i < nums.length; i++) { | ||
| int n = nums[i]; | ||
| if (currAnd <= andMax) { | ||
| count++; | ||
| sum += currAnd; | ||
| currAnd = n; | ||
| } | ||
| currAnd &= n; | ||
| } | ||
| if (currAnd <= andMax) { | ||
| count++; | ||
| sum += currAnd; | ||
| } | ||
| return sum <= andMax ? count : 1; | ||
| } | ||
| } |
44 changes: 44 additions & 0 deletions 44 ...in/java/g2801_2900/s2871_split_array_into_maximum_number_of_subarrays/readme.md
This file contains hidden or bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters. Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,44 @@ | ||
| 2871\. Split Array Into Maximum Number of Subarrays | ||
| | ||
| Medium | ||
| | ||
| You are given an array `nums` consisting of **non-negative** integers. | ||
| | ||
| We define the score of subarray `nums[l..r]` such that `l <= r` as `nums[l] AND nums[l + 1] AND ... AND nums[r]` where **AND** is the bitwise `AND` operation. | ||
| | ||
| Consider splitting the array into one or more subarrays such that the following conditions are satisfied: | ||
| | ||
| * **E****ach** element of the array belongs to **exactly** one subarray. | ||
| * The sum of scores of the subarrays is the **minimum** possible. | ||
| | ||
| Return _the **maximum** number of subarrays in a split that satisfies the conditions above._ | ||
| | ||
| A **subarray** is a contiguous part of an array. | ||
| | ||
| **Example 1:** | ||
| | ||
| **Input:** nums = [1,0,2,0,1,2] | ||
| | ||
| **Output:** 3 | ||
| | ||
| **Explanation:** We can split the array into the following subarrays: | ||
| - [1,0]. The score of this subarray is 1 AND 0 = 0. | ||
| - [2,0]. The score of this subarray is 2 AND 0 = 0. | ||
| - [1,2]. The score of this subarray is 1 AND 2 = 0. | ||
| | ||
| The sum of scores is 0 + 0 + 0 = 0, which is the minimum possible score that we can obtain. | ||
| | ||
| It can be shown that we cannot split the array into more than 3 subarrays with a total score of 0. So we return 3. | ||
| | ||
| **Example 2:** | ||
| | ||
| **Input:** nums = [5,7,1,3] | ||
| | ||
| **Output:** 1 | ||
| | ||
| **Explanation:** We can split the array into one subarray: [5,7,1,3] with a score of 1, which is the minimum possible score that we can obtain. It can be shown that we cannot split the array into more than 1 subarray with a total score of 1. So we return 1. | ||
| | ||
| **Constraints:** | ||
| | ||
| * <code>1 <= nums.length <= 10<sup>5</sup></code> | ||
| * <code>0 <= nums[i] <= 10<sup>6</sup></code> |
50 changes: 50 additions & 0 deletions 50 src/main/java/g2801_2900/s2872_maximum_number_of_k_divisible_components/Solution.java
This file contains hidden or bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters. Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,50 @@ | ||
| package g2801_2900.s2872_maximum_number_of_k_divisible_components; | ||
| | ||
| // #Hard #Dynamic_Programming #Tree #Depth_First_Search | ||
| // #2023_12_21_Time_24_ms_(93.51%)_Space_65.3_MB_(19.48%) | ||
| | ||
| import java.util.ArrayList; | ||
| import java.util.List; | ||
| | ||
| public class Solution { | ||
| private int ans = 0; | ||
| | ||
| public int maxKDivisibleComponents(int n, int[][] edges, int[] values, int k) { | ||
| List<List<Integer>> adj = new ArrayList<>(); | ||
| for (int i = 0; i < n; i++) { | ||
| adj.add(new ArrayList<>()); | ||
| } | ||
| for (int[] edge : edges) { | ||
| int start = edge[0]; | ||
| int end = edge[1]; | ||
| adj.get(start).add(end); | ||
| adj.get(end).add(start); | ||
| } | ||
| boolean[] isVis = new boolean[n]; | ||
| isVis[0] = true; | ||
| get(0, -1, adj, isVis, values, k); | ||
| return ans; | ||
| } | ||
| | ||
| private long get( | ||
| int curNode, | ||
| int parent, | ||
| List<List<Integer>> adj, | ||
| boolean[] isVis, | ||
| int[] values, | ||
| long k) { | ||
| long sum = values[curNode]; | ||
| for (int ele : adj.get(curNode)) { | ||
| if (ele != parent && !isVis[ele]) { | ||
| isVis[ele] = true; | ||
| sum += get(ele, curNode, adj, isVis, values, k); | ||
| } | ||
| } | ||
| if (sum % k == 0) { | ||
| ans++; | ||
| return 0; | ||
| } else { | ||
| return sum; | ||
| } | ||
| } | ||
| } |
52 changes: 52 additions & 0 deletions 52 src/main/java/g2801_2900/s2872_maximum_number_of_k_divisible_components/readme.md
This file contains hidden or bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters. Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,52 @@ | ||
| 2872\. Maximum Number of K-Divisible Components | ||
| | ||
| Hard | ||
| | ||
| There is an undirected tree with `n` nodes labeled from `0` to `n - 1`. You are given the integer `n` and a 2D integer array `edges` of length `n - 1`, where <code>edges[i] = [a<sub>i</sub>, b<sub>i</sub>]</code> indicates that there is an edge between nodes <code>a<sub>i</sub></code> and <code>b<sub>i</sub></code> in the tree. | ||
| | ||
| You are also given a **0-indexed** integer array `values` of length `n`, where `values[i]` is the **value** associated with the <code>i<sup>th</sup></code> node, and an integer `k`. | ||
| | ||
| A **valid split** of the tree is obtained by removing any set of edges, possibly empty, from the tree such that the resulting components all have values that are divisible by `k`, where the **value of a connected component** is the sum of the values of its nodes. | ||
| | ||
| Return _the **maximum number of components** in any valid split_. | ||
| | ||
| **Example 1:** | ||
| | ||
| 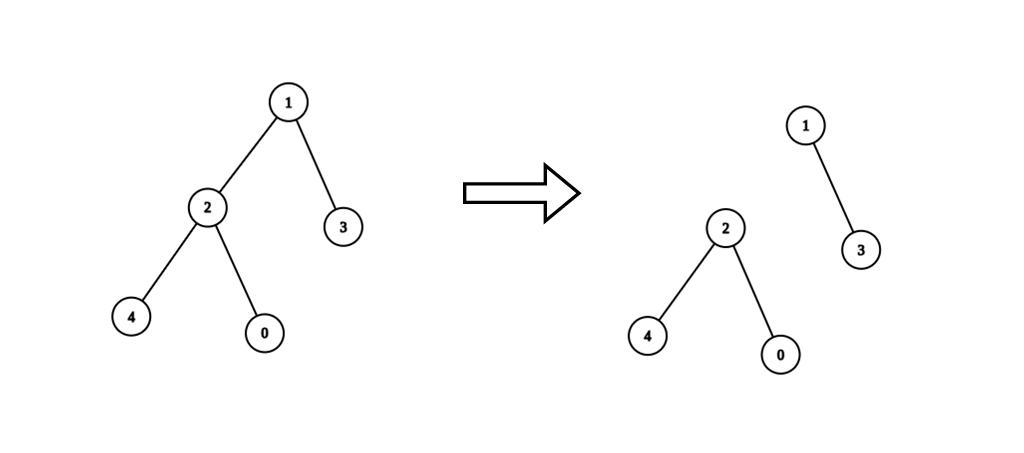 | ||
| | ||
| **Input:** n = 5, edges = [[0,2],[1,2],[1,3],[2,4]], values = [1,8,1,4,4], k = 6 | ||
| | ||
| **Output:** 2 | ||
| | ||
| **Explanation:** We remove the edge connecting node 1 with 2. The resulting split is valid because: | ||
| - The value of the component containing nodes 1 and 3 is values[1] + values[3] = 12. | ||
| - The value of the component containing nodes 0, 2, and 4 is values[0] + values[2] + values[4] = 6. | ||
| | ||
| It can be shown that no other valid split has more than 2 connected components. | ||
| | ||
| **Example 2:** | ||
| | ||
| 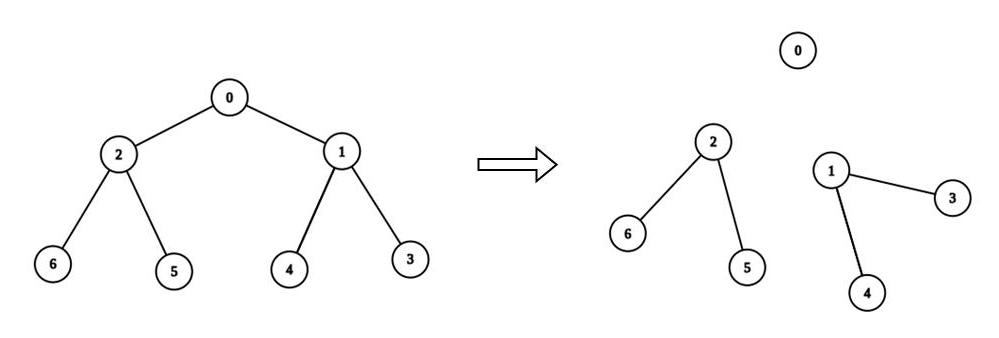 | ||
| | ||
| **Input:** n = 7, edges = [[0,1],[0,2],[1,3],[1,4],[2,5],[2,6]], values = [3,0,6,1,5,2,1], k = 3 | ||
| | ||
| **Output:** 3 | ||
| | ||
| **Explanation:** We remove the edge connecting node 0 with 2, and the edge connecting node 0 with 1. The resulting split is valid because: | ||
| - The value of the component containing node 0 is values[0] = 3. | ||
| - The value of the component containing nodes 2, 5, and 6 is values[2] + values[5] + values[6] = 9. | ||
| - The value of the component containing nodes 1, 3, and 4 is values[1] + values[3] + values[4] = 6. | ||
| | ||
| It can be shown that no other valid split has more than 3 connected components. | ||
| | ||
| **Constraints:** | ||
| | ||
| * <code>1 <= n <= 3 * 10<sup>4</sup></code> | ||
| * `edges.length == n - 1` | ||
| * `edges[i].length == 2` | ||
| * <code>0 <= a<sub>i</sub>, b<sub>i</sub> < n</code> | ||
| * `values.length == n` | ||
| * <code>0 <= values[i] <= 10<sup>9</sup></code> | ||
| * <code>1 <= k <= 10<sup>9</sup></code> | ||
| * Sum of `values` is divisible by `k`. | ||
| * The input is generated such that `edges` represents a valid tree. |
27 changes: 27 additions & 0 deletions 27 src/main/java/g2801_2900/s2873_maximum_value_of_an_ordered_triplet_i/Solution.java
This file contains hidden or bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters. Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,27 @@ | ||
| package g2801_2900.s2873_maximum_value_of_an_ordered_triplet_i; | ||
| | ||
| // #Easy #Array #2023_12_21_Time_0_ms_(100.00%)_Space_42_MB_(10.64%) | ||
| | ||
| public class Solution { | ||
| public long maximumTripletValue(int[] nums) { | ||
| final int n = nums.length; | ||
| final int[] iNumMaxs = new int[n]; | ||
| int prev = 0; | ||
| for (int i = 0; i < n; i++) { | ||
| if (nums[i] <= prev) { | ||
| iNumMaxs[i] = prev; | ||
| } else { | ||
| prev = iNumMaxs[i] = nums[i]; | ||
| } | ||
| } | ||
| long result = 0; | ||
| int kNumMax = nums[n - 1]; | ||
| for (int j = n - 2; j > 0; j--) { | ||
| result = Math.max(result, (long) (iNumMaxs[j - 1] - nums[j]) * kNumMax); | ||
| if (nums[j] > kNumMax) { | ||
| kNumMax = nums[j]; | ||
| } | ||
| } | ||
| return result; | ||
| } | ||
| } |
Oops, something went wrong.
Add this suggestion to a batch that can be applied as a single commit. This suggestion is invalid because no changes were made to the code. Suggestions cannot be applied while the pull request is closed. Suggestions cannot be applied while viewing a subset of changes. Only one suggestion per line can be applied in a batch. Add this suggestion to a batch that can be applied as a single commit. Applying suggestions on deleted lines is not supported. You must change the existing code in this line in order to create a valid suggestion. Outdated suggestions cannot be applied. This suggestion has been applied or marked resolved. Suggestions cannot be applied from pending reviews. Suggestions cannot be applied on multi-line comments. Suggestions cannot be applied while the pull request is queued to merge. Suggestion cannot be applied right now. Please check back later.
Uh oh!
There was an error while loading. Please reload this page.