二叉树之方法实现

发布时间：2020-06-30 14:19:59 来源：网络阅读：460 作者：汇天下豪杰栏目：编程语言

1、二叉树上的操作

均是C++实现先根序创建二叉树及其其它方法

我认为在二叉树的创建方法和遍历以外，以下方法值得我们关注：

public:     int size()const;  //求结点个数     int height()const;  //求树的高度     BinTreeNode<Type>* root_1()const; //求根节点     BinTreeNode<Type>* leftChild(BinTreeNode<Type>* cur)const;  //求当前结点的左孩子     BinTreeNode<Type>* rightChild(BinTreeNode<Type>* cur)const; //求当前结点的右孩子     BinTreeNode<Type>* find(const Type &key)const;              //查找当前结点     BinTreeNode<Type>* parent(BinTreeNode<Type>* cur)const;     //查找当前结点的父结点     void makeEmpty();                                           //将二叉树置空     bool equal(const BinTree<Type> &t)const;                    //两个二叉树是否相同的比较     BinTreeNode<Type>* copy(BinTreeNode<Type> *t)const;         //拷贝构造函数的方法，复制一个二叉树

2、方法一一实现：

(1)、求结点个数

template<typename Type> int BinTree<Type>::size(BinTreeNode<Type> *t)const{     if(t == NULL){         return 0;     }     return size(t->leftChild) + size(t->rightChild) + 1; }

(2)、求树的高度

template<typename Type> int BinTree<Type>::height(BinTreeNode<Type> *t)const{     if(t == NULL){         return 0;     }     int leftHeight = height(t->leftChild);     int rightHeight = height(t->rightChild);     return (leftHeight > rightHeight ? leftHeight : rightHeight) + 1; }

(3)、查找当前结点

template<typename Type> BinTreeNode<Type>* BinTree<Type>::find(const Type &key, BinTreeNode<Type> *t)const{     if(t == NULL){         return NULL;     }     if(t->data == key){         return t;     }     BinTreeNode<Type> *p = find(key, t->leftChild);     if(p != NULL){         return p;     }     return find(key, t->rightChild); }

(4)、查找当前结点的父结点

template<typename Type> BinTreeNode<Type>* BinTree<Type>::parent(BinTreeNode<Type>* cur, BinTreeNode<Type> *t)const{     if(t == NULL || cur == NULL || cur == t){         return NULL;     }     if(t->leftChild == cur || t->rightChild == cur){         return t;     }        //思路：利用父的孩子节点和当前节点比较     BinTreeNode<Type> *p = parent(cur, t->leftChild);     if(p != NULL){         return p;     }     return parent(cur, t->rightChild); }

(5)、将二叉树置空

template<typename Type> void BinTree<Type>::makeEmpty(BinTreeNode<Type> *t){     if(t != NULL){         makeEmpty(t->leftChild);         makeEmpty(t->rightChild);         delete t;     } }

(6)、两个二叉树是否相同的比较

template<typename Type> bool BinTree<Type>::equal(BinTreeNode<Type> *t, BinTreeNode<Type> *t1)const{     if(t == NULL && t1 == NULL){  //取反判断与这个是一个道理         return true;     }     if(t != NULL && t1!= NULL && t->data == t1->data && equal(t->leftChild, t1->leftChild)         && equal(t->rightChild, t1->rightChild)){         return true;     }else{         return false;     } }

(7)、拷贝一个二叉树

template<typename Type> BinTreeNode<Type>* BinTree<Type>::copy(BinTreeNode<Type> *t)const{     BinTreeNode<Type>* tmp;     if(t == NULL){         return NULL;     }else{         tmp = new BinTreeNode<Type>(t->data);         tmp->leftChild = copy(t->leftChild);         tmp->rightChild = copy(t->rightChild);     }     return tmp; }

以上的这些方法都是利用二叉树的性质递归实现，比较好想清楚，就不做解释了，实在有问题，画画图就会好很多。

3、二叉树的所有方法，测试，及测试结果如下：

(1)、所有关于二叉树的代码：

#ifndef _BIN_TREE_H_ #define _BIN_TREE_H_ #include<iostream> #include<stack>  //非递归遍历引入栈 #include<queue>  //层次遍历引入队列 using namespace std; template<typename Type> //为的是声明友元类，调用BinTreeNode<Type>的私有数据 class BinTree; template<typename Type>  //BinTreeNode类 class BinTreeNode{        friend class BinTree<Type>; public:     BinTreeNode() : data(Type()), leftChild(NULL), rightChild(NULL){}     BinTreeNode(Type value, BinTreeNode<Type> *left = NULL, BinTreeNode<Type> *right = NULL) :     data(value), leftChild(left), rightChild(right){}     ~BinTreeNode(){} private:     Type data;     BinTreeNode *leftChild;     BinTreeNode *rightChild; }; /////////////////////////////////////////////////////////////////////////////// template<typename Type>   //BinTree类 class BinTree{ public:     BinTree() : root(NULL){}     BinTree(Type ref) : root(NULL), refval(ref){}     BinTree(const BinTree &t){         root = copy(t.root);  //调用拷贝方法     }     ~BinTree(){         makeEmpty();  //析构函数这里将二叉树置空         root = NULL;         } public:                 //创建二叉树     void createBinTree();     void createBinTree(const char *str);     void createBinTree(const char *VLR, const char *LVR, int n);     void createBinTree_1(const char *LVR, const char *LRV, int n); public:                //递归遍历     void prevOrder()const;     void inOrder()const;     void endOrder()const; public:               //各种方法的声明     int size()const;     int height()const;     BinTreeNode<Type>* root_1()const; //以下的三个方法比较简单，就不在进行调用保护方法了；     BinTreeNode<Type>* leftChild(BinTreeNode<Type>* cur)const;     BinTreeNode<Type>* rightChild(BinTreeNode<Type>* cur)const;     BinTreeNode<Type>* find(const Type &key)const;     BinTreeNode<Type>* parent(BinTreeNode<Type>* cur)const;     void makeEmpty();     bool equal(const BinTree<Type> &t)const;     BinTreeNode<Type>* copy(BinTreeNode<Type> *t)const; public:              //非递归遍历     void prevOrder_1()const;     void inOrder_1()const;     void endOrder_1()const;     void levelOrder()const; //puublic:供外界提供的接口， //////////////////////////////////////////////////////////////////////////////// protected:                 //protected:供自己函数内部调用，写保护方法     void prevOrder_1(BinTreeNode<Type>* t)const;     void inOrder_1(BinTreeNode<Type>* t)const;     void endOrder_1(BinTreeNode<Type>* t)const;     void levelOrder(BinTreeNode<Type>* t)const; protected:     int size(BinTreeNode<Type> *t)const;     int height(BinTreeNode<Type> *t)const;     BinTreeNode<Type>* find(const Type &key, BinTreeNode<Type> *t)const;     BinTreeNode<Type>* parent(BinTreeNode<Type>* cur, BinTreeNode<Type> *t)const;     void makeEmpty(BinTreeNode<Type>* t);     bool equal(BinTreeNode<Type> *t, BinTreeNode<Type> *t1)const; protected:     void prevOrder(BinTreeNode<Type> *t)const;     void inOrder(BinTreeNode<Type> *t)const;     void endOrder(BinTreeNode<Type> *t)const; protected :     void createBinTree(BinTreeNode<Type> *&t);     BinTreeNode<Type>* createBinTree_1();     void createBinTree(const char *&str, BinTreeNode<Type> *&t);     BinTreeNode<Type>* createBinTree_1(const char *&str);     void createBinTree(BinTreeNode<Type> *&t, const char *VLR, const char *LVR, int n);     void createBinTree_1(BinTreeNode<Type> *&t, const char *LVR, const char *LRV, int n);                          //以上都只是在类内声明； private:     BinTreeNode<Type> *root;     Type               refval;  //'#' }; /////////////////////////////////////////////////////////////////////////////// template<typename Type>  //类外实现公有方法的调用 void BinTree<Type>::createBinTree(){  //创建二叉树     //createBinTree(root);     root = createBinTree_1(); } template<typename Type> void BinTree<Type>::prevOrder()const{ //先序递归遍历     cout<<"先根序如下: "<<endl;     prevOrder(root); } template<typename Type> void BinTree<Type>::inOrder()const{ //中序递归遍历     cout<<"中根序如下: "<<endl;     inOrder(root); } template<typename Type> void BinTree<Type>::endOrder()const{  //后序递归遍历     cout<<"后根序如下: "<<endl;     endOrder(root); } template<typename Type> void BinTree<Type>::createBinTree(const char *str){ //创建二叉树 //    createBinTree(str, root);     root = createBinTree_1(str); } template<typename Type> int BinTree<Type>::size()const{  //求结点个数     return size(root); } template<typename Type> int BinTree<Type>::height()const{ //求树的高度     return height(root); } template<typename Type> BinTreeNode<Type>* BinTree<Type>::root_1()const{ //求根节点     return root; } template<typename Type> BinTreeNode<Type>* BinTree<Type>::leftChild(BinTreeNode<Type>* cur)const{ //求当前结点的左孩子     return cur->leftChild; } template<typename Type> BinTreeNode<Type>* BinTree<Type>::rightChild(BinTreeNode<Type>* cur)const{  //求当前结点的右孩子     return cur->rightChild; } template<typename Type> BinTreeNode<Type>* BinTree<Type>::find(const Type &key)const{  //查找当前结点     return find(key, root); } template<typename Type> BinTreeNode<Type>* BinTree<Type>::parent(BinTreeNode<Type>* cur)const{ //查找当前结点的父结点     return parent(cur, root); } template<typename Type> void BinTree<Type>::makeEmpty(){ //将二叉树置空     makeEmpty(root); } template<typename Type> bool BinTree<Type>::equal(const BinTree<Type> &t)const{ //两个二叉树是否相同的比较     return equal(t.root, root); } template<typename Type> void BinTree<Type>::prevOrder_1()const{  //非递归先序     prevOrder_1(root); } template<typename Type> void BinTree<Type>::inOrder_1()const{   //非递归中序     inOrder_1(root); } template<typename Type> void BinTree<Type>::endOrder_1()const{   //非递归后序     endOrder(root); } template<typename Type> void BinTree<Type>::levelOrder()const{   //层次遍历     levelOrder(root); } template<typename Type> void BinTree<Type>::createBinTree(const char *VLR, const char *LVR, int n){ //创建二叉树     createBinTree(root, VLR, LVR, n); } template<typename Type>  void BinTree<Type>::createBinTree_1(const char *LVR, const char *LRV, int n){ //创建二叉树     createBinTree_1(root, LVR, LRV, n); } ////////////////////////////////////////////////////////////////////////////////////////// template<typename Type>  //以下的都是写保护的方法，供自己使用 void BinTree<Type>::createBinTree_1(BinTreeNode<Type> *&t, const char *LVR, const char *LRV, int n){  //中序和后序创建二叉树     if(n == 0){         t = NULL;         return;     }     int k = 0;     while(LVR[k] != LRV[n-1]){         k++;     }     t = new BinTreeNode<Type>(LVR[k]);          createBinTree_1(t->rightChild, LVR+k+1, LRV+k, n-k-1);     createBinTree_1(t->leftChild, LVR, LRV, k); } template<typename Type> void BinTree<Type>::createBinTree(BinTreeNode<Type> *&t, const char *VLR, const char *LVR, int n){   //先序和中序创建二叉树     if(n == 0){         t = NULL;         return;     }     int k = 0;     while(LVR[k] != VLR[0]){         k++;     }     t = new BinTreeNode<Type>(LVR[k]);     createBinTree(t->leftChild, VLR+1, LVR, k);     createBinTree(t->rightChild, VLR+k+1, LVR+k+1, n-k-1); } template<typename Type> void BinTree<Type>::levelOrder(BinTreeNode<Type>* t)const{  //层次遍历     queue<BinTreeNode<Type> *> qu;     BinTreeNode<Type> *p;     if(t != NULL){         qu.push(t);         while(!qu.empty()){             p = qu.front();             qu.pop();             cout<<p->data<<" ";             if(p->leftChild){                 qu.push(p->leftChild);             }             if(p->rightChild){                 qu.push(p->rightChild);             }         }     } } typedef enum{L, R}Tag; template<typename Type> class stkNode{ public:     stkNode(BinTreeNode<Type> *p = NULL) : ptr(p), tag(L){} public:     BinTreeNode<Type> *ptr;     Tag                   tag; //L R }; template<typename Type> void BinTree<Type>::endOrder_1(BinTreeNode<Type>* t)const{  //非递归后序     stkNode<Type> n;     stack<stkNode<Type>> st;     BinTreeNode<Type> *p = t;          do{         while(p != NULL){             n.ptr = p;             n.tar = L;             st.push(n);             p = p->leftChild;         }         bool isRun = true;         while(isRun && !st.empty()){             n = st.top();             st.pop();             switch(n.tag){             case L:                 p = n.ptr;                 n.tag = R;                 st.push(n);                 p = p->rightChild;                 isRun = false;                 break;             case R:                 cout<<n.ptr->data<<" ";                 break;             }         }     }while(!st.empty());//不用p1=NULL,因为当栈空时，最后一个节点刚好被访问完成。 } template<typename Type> void BinTree<Type>::inOrder_1(BinTreeNode<Type>* t)const{  //非递归中序     stack<BinTreeNode<Type> *> st;     BinTreeNode<Type> *p = t;     do{         while(p != NULL){             st.push(p);             p = p->leftChild;         }         if(!st.empty()){             p = st.top();             st.pop();             cout<<p->data<<" ";             p = p->rightChild;         }//中序遍历时，当root出栈时，此时占空，     }while(p != NULL || !st.empty()); //为根的时候右边还要入栈。 } template<typename Type> void BinTree<Type>::prevOrder_1(BinTreeNode<Type>* t)const{  //非递归先序     stack<BinTreeNode<Type> *> st;     BinTreeNode<Type> *tmp;     if(t != NULL){         st.push(t);         while(!st.empty()){             tmp = st.top();             st.pop();             cout<<tmp->data<<" ";             if(tmp->rightChild){                 st.push(tmp->rightChild);             }             if(tmp->leftChild){                 st.push(tmp->leftChild);             }         }     } } template<typename Type> BinTreeNode<Type>* BinTree<Type>::copy(BinTreeNode<Type> *t)const{  //拷贝函数     BinTreeNode<Type>* tmp;     if(t == NULL){         return NULL;     }else{         tmp = new BinTreeNode<Type>(t->data);         tmp->leftChild = copy(t->leftChild);         tmp->rightChild = copy(t->rightChild);     }     return tmp; } template<typename Type> bool BinTree<Type>::equal(BinTreeNode<Type> *t, BinTreeNode<Type> *t1)const{  //两个二叉树是否相同的比较     if(t == NULL && t1 == NULL){  //取反判断与这个是一个道理         return true;     }     if(t != NULL && t1!= NULL && t->data == t1->data && equal(t->leftChild, t1->leftChild)         && equal(t->rightChild, t1->rightChild)){         return true;     }else{         return false;     } } template<typename Type> void BinTree<Type>::makeEmpty(BinTreeNode<Type> *t){  //将二叉树置空     if(t != NULL){         makeEmpty(t->leftChild);         makeEmpty(t->rightChild);         delete t;     } } template<typename Type> BinTreeNode<Type>* BinTree<Type>::parent(BinTreeNode<Type>* cur, BinTreeNode<Type> *t)const{  //查找当前结点的父结点     if(t == NULL || cur == NULL || cur == t){         return NULL;     }     if(t->leftChild == cur || t->rightChild == cur){         return t;     }        //思路：利用父的孩子节点和当前节点比较     BinTreeNode<Type> *p = parent(cur, t->leftChild);     if(p != NULL){         return p;     }     return parent(cur, t->rightChild); } template<typename Type> BinTreeNode<Type>* BinTree<Type>::find(const Type &key, BinTreeNode<Type> *t)const{   //查找当前结点     if(t == NULL){         return NULL;     }     if(t->data == key){         return t;     }     BinTreeNode<Type> *p = find(key, t->leftChild);     if(p != NULL){         return p;     }     return find(key, t->rightChild); } template<typename Type> int BinTree<Type>::height(BinTreeNode<Type> *t)const{  //求树的高度     if(t == NULL){         return 0;     }     int leftHeight = height(t->leftChild);     int rightHeight = height(t->rightChild);     return (leftHeight > rightHeight ? leftHeight : rightHeight) + 1; } template<typename Type> int BinTree<Type>::size(BinTreeNode<Type> *t)const{  //求结点个数     if(t == NULL){         return 0;     }     return size(t->leftChild) + size(t->rightChild) + 1; } template<typename Type> BinTreeNode<Type>* BinTree<Type>::createBinTree_1(const char *&str){  //创建二叉树     BinTreeNode<Type> *t;     if(refval == *str){         t = NULL;     }else{         t = new BinTreeNode<Type>(*str);         t->leftChild = createBinTree_1(++str);         t->rightChild = createBinTree_1(++str);     }     return t; } template<typename Type> void BinTree<Type>::createBinTree(const char *&str, BinTreeNode<Type> *&t){  //创建二叉树     if(*str == refval){         t = NULL;     }else{         t = new BinTreeNode<Type>(*str);         createBinTree(++str, t->leftChild);  //前加，后加不一样！！！在这里，就是传引用，保证每次字符串都是往后走的         createBinTree(++str, t->rightChild);     } } template<typename Type> BinTreeNode<Type>* BinTree<Type>::createBinTree_1(){  //创建二叉树     Type createData;     cin>>createData;     BinTreeNode<Type> *t;     if(refval == createData){         t = NULL;     }else{         t = new BinTreeNode<Type>(createData);         t->leftChild = createBinTree_1();         t->rightChild = createBinTree_1();     }     return t; } template<typename Type> void BinTree<Type>::endOrder(BinTreeNode<Type> *t)const{  //后序递归遍历     if(t == NULL){         return;     }else{         endOrder(t->leftChild);         endOrder(t->rightChild);         cout<<t->data<<" ";     } } template<typename Type>  void BinTree<Type>::inOrder(BinTreeNode<Type> *t)const{  //中序递归遍历     if(t == NULL){         return;     }else{         inOrder(t->leftChild);         cout<<t->data<<" ";         inOrder(t->rightChild);     } } template<typename Type> void BinTree<Type>::prevOrder(BinTreeNode<Type> *t)const{  //先序递归遍历     if(t == NULL){         return;     }else{         cout<<t->data<<" ";         prevOrder(t->leftChild);         prevOrder(t->rightChild);     } } //根据先根序创建二叉树 template<typename Type> void BinTree<Type>::createBinTree(BinTreeNode<Type> *&t){  //创建二叉树     Type createData;     cin>>createData;     if(refval == createData){         t = NULL;     }else{         t = new BinTreeNode<Type>(createData);         createBinTree(t->leftChild);         createBinTree(t->rightChild);     } } #endif

以上代码我采用折叠的方式进行写的。类外公有调用下面紧跟保护方法的实现；

(2)、测试代码

#include"BinTree.h" //ABC##DE##F##G#H## /* 先根序如下: A B C D E F G H 中根序如下: C B E D F A G H 后根序如下: C E F D B H G A */ int main(void){ //    char *VLR = "ABCDEFGH"; //    char *LVR = "CBEDFAGH"; //    char *LRV = "CEFDBHGA"; //    BinTree<char> bt; //对象初始化不写'#'； //    int n = strlen(VLR); //    bt.createBinTree(VLR, LVR, n); //在这里创建二叉树不用'#'结束，因为是由先序和中序创建，不看结束标志'#'; //    bt.createBinTree_1(LVR, LRV, n); //    bt.prevOrder(); //    cout<<endl;     //bt.createBinTree(VLR, LRV, n); 不能创建 /*     BinTree<char> bt('#');     char *str = "ABC##DE##F##G#H##"; //    char *str = "ABC##DE###G#H##";     bt.createBinTree(str);     BinTree<char> bt1(bt);     bt1.levelOrder();     cout<<endl;      */        /*          //    st.createBinTree();     BinTree<char> bt('#');     BinTree<char> bt1('#');     char *str = "ABC##DE##F##G#H##";     bt.createBinTree(str);     bt1.createBinTree(str);  //构建的是一颗空树,引用传递构建，原先字符串已经为空！     if(bt.equal(bt1)){         cout<<"相等"<<endl;     }else{         cout<<"不相等"<<endl;     } */         BinTree<char> bt('#');     char *str = "ABC##DE##F##G#H##";     bt.createBinTree(str);     cout<<bt.size()<<endl;     cout<<bt.height()<<endl;     BinTreeNode<char> *p = bt.find('H');     BinTreeNode<char> *t = bt.find('G');     printf("%p\n", t);     BinTreeNode<char> *q = bt.parent(p);     printf("%p\n", q);     bt.prevOrder();     cout<<endl;     bt.inOrder();     cout<<endl;     bt.endOrder();     cout<<endl;          return 0; }

这是所有测试要用的代码，在编写时，写一个方法测试一个，将测试过的就注释起来了；

(3)、部分测试结果

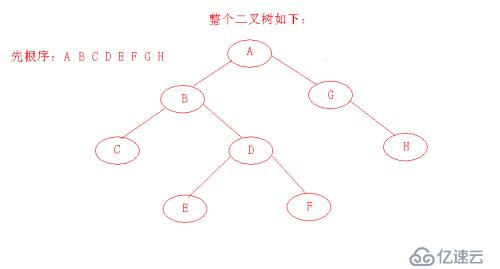
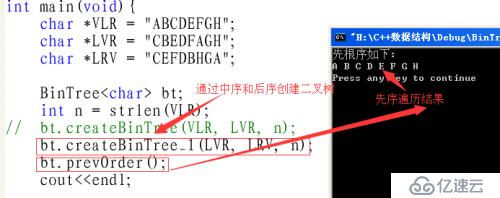
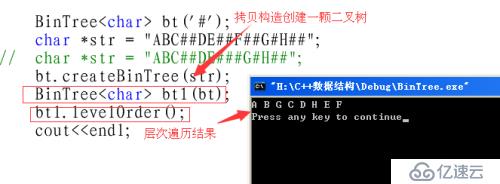
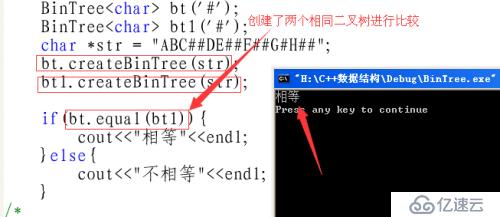
二叉树之方法实现