数据结构(07)_队列

1. .队列的概念和实现

1.1.队列的概念

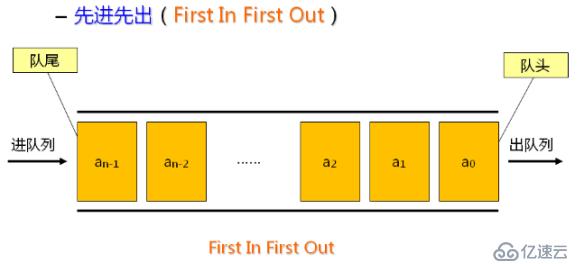
队列是一种特殊的线性表，仅能在线性表的两端进行操作。

• -队头（front）取出数据元素的一端；
• -队尾（rear）插入数据元素的一端。
  队列的特性：
  
  队列的常用操作：
  创建和销毁；出队和入队；清空队列；获取队首元素；获取队列长度
  
  队列声明（接口）：

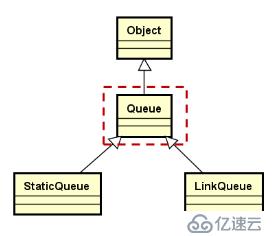
  template < typename T > class Queue { public: virtual void enqueue(const T& e) = 0; virtual void dequeue() = 0; virtual T front() const = 0; virtual void clear() = 0; virtual int length() const = 0; };

  1.2.Stati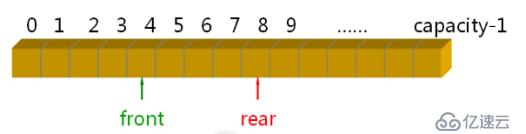cQueu

  顺序队列的实现：
  
  设计要点：
  类模板，使用原生数组作为队列 存储空间，使用模板参数决定队列的最大容量；

  template < typename T, int N > class StaticQueue : public Queue<T> { protected: T m_space[N]; int m_front; int m_rear; int m_length; public: StaticQueue() void enqueue(const T& e) void dequeue() T front() const void clear() int length() const int capacity() const };

  注意事项:
  StaticQueue实现要点：（循环计数法） 提高队列操作的效率（本质上时循环队列）
  关键操作：

• 入队：m_rear = (m_rear + 1) % N;
• 出队：m_front = (m_front + 1) % N;
  队列状态：
• 队空：(m_length == 0) && (m_front == m_rear)

• 队满：(m_length == N) && (m_front == m_rear)
  StaticQueue最终实现：

  template < typename T, int N > class StaticQueue : public Queue<T> { protected: T m_space[N]; int m_front; int m_rear; int m_length; public: StaticQueue() //O(1) { m_front = 0; m_rear = 0; m_length = 0; } void enqueue(const T& e) //O(1) { if(m_length < N) { m_space[m_rear] = e; m_rear = (m_rear + 1) % N; m_length++; } else { THROW_EXCEPTION(InvalidOperationException, "no space in current staticqueue..."); } } void dequeue() //O(1) { if(m_length > 0) { m_front = (m_front + 1) % N; m_length--; } else { THROW_EXCEPTION(InvalidOperationException, "no element in current staticqueue..."); } } T front() const //O(1) { if(m_length > 0) { return m_space[m_front]; } else { THROW_EXCEPTION(InvalidOperationException, "no element in current staticqueue..."); } } void clear() //O(1) { m_front = 0; m_rear = 0; m_length = 0; } int length() const //O(1) { return m_length; } int capacity() const //O(1) { return N; } bool is_empty() //O(1) { return (m_length == 0) && (m_front == m_rear); } bool is_full() //O(1) { return (m_length == N) && (m_front == m_rear); } };

  2.链式队列

  2.1.LinkQueue

  顺序队列的缺陷：当数据为类类型时，StaticQueue的对象在创建时，会多次调用元素类型的构造函数，影响效率。所以我们采用链式存储结构来实现队列。
  
  设计要点：
  1.类模板，继承自抽象父类Queue;
  2.在内部使用链式结构实现元素的存储
  3.只在链表的头部和尾部进行操作。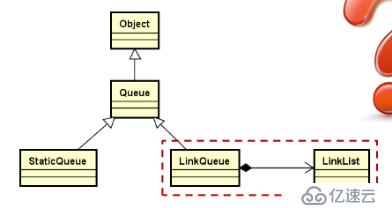
  
  LinkQueue声明：

  template <typename T> class LinkQueue : public Queue<T> { protected: LinkList<T> m_list; public: LinkQueue(){} void enqueue(const T& e) //O(n) void dequeue() //O(1) T front() const //O(1) void clear() //O(n) int length() const //O(1) };

  LinkQueue最终实现：

  template <typename T> class LinkQueue : public Queue<T> { protected: LinkList<T> m_list; public: LinkQueue(){} void enqueue(const T& e) //O(n) { m_list.insert(e); } void dequeue() //O(1) { if(m_list.length() > 0) { m_list.remove(0); } else { THROW_EXCEPTION(InvalidOperationException, "no elemet in current LinkQueue..."); } } T front() const //O(1) { if(m_list.length() > 0) { return m_list.get(0); } else { THROW_EXCEPTION(InvalidOperationException, "no elemet in current LinkQueue..."); } } void clear() //O(n) { while (m_list.length() > 0) { m_list.remove(0); } } int length() const //O(1) { return m_list.length(); } };

  LinkQueue中，入队操作由于只能操作队列的尾部（链表的最后位置），要进行遍历操作，所以时间复杂度为O(n)，可以使用双向循环链表代替单链表来解决这个问题。