Single-Source Shortest Paths, Nonnegative Weights

The single source shortest path algorithm (for non-negative weight) is also known Dijkstra algorithm. There is a given graph G(V,E) with its adjacency matrix representation, and a source vertex is also provided. Dijkstra’s algorithm to find the minimum shortest path between source vertex to any other vertex of the graph G.

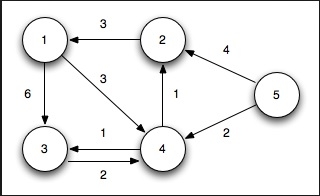
From starting node to any other node, find the smallest distances. In this problem the graph is represented using the adjacency matrix. (Cost matrix and adjacency matrix is similar for this purpose).

Input − The adjacency matrix −

0 3 6 ∞ ∞ ∞ ∞ 3 0 2 1 ∞ ∞ ∞ 6 2 0 1 4 2 ∞ ∞ 1 1 0 2 ∞ 4 ∞ ∞ 4 2 0 2 1 ∞ ∞ 2 ∞ 2 0 1 ∞ ∞ ∞ 4 1 1 0

Output −

0 to 1, Using: 0, Cost: 3 0 to 2, Using: 1, Cost: 5 0 to 3, Using: 1, Cost: 4 0 to 4, Using: 3, Cost: 6 0 to 5, Using: 2, Cost: 7 0 to 6, Using: 4, Cost: 7

Algorithm

dijkstraShortestPath(n, dist, next, start)

Input − Total number of nodes n, distance list for each vertex, next list to store which node comes next, and the seed or start vertex.

Output − The shortest paths from start to all other vertices.

Begin    create a status list to hold the current status of the selected node    for all vertices u in V do       status[u] := unconsidered       dist[u] := distance from source using cost matrix       next[u] := start    done    status[start] := considered, dist[start] := 0 and next[start] := φ    while take unconsidered vertex u as distance is minimum do       status[u] := considered       for all vertex v in V do          if status[v] = unconsidered then          if dist[v] > dist[u] + cost[u,v] then             dist[v] := dist[u] + cost[u,v]             next[v] := u       done    done End

Example(C++)

#include<iostream> #define V 7 #define INF 999 using namespace std; //Cost matrix of the graph int costMat[V][V] = {    {0, 3, 6, INF, INF, INF, INF},    {3, 0, 2, 1, INF, INF, INF},    {6, 2, 0, 1, 4, 2, INF},    {INF, 1, 1, 0, 2, INF, 4},    {INF, INF, 4, 2, 0, 2, 1},    {INF, INF, 2, INF, 2, 0, 1},    {INF, INF, INF, 4, 1, 1, 0} }; int minimum(int *status, int *dis, int n){    int i, min, index;    min = INF;    for(i = 0; i<n; i++)       if(dis[i] < min && status[i] == 1){       min = dis[i];       index = i;    }    if(status[index] == 1)       return index;//minimum unconsidered vertex distance    else       return -1;//when all vertices considered } void dijkstra(int n, int *dist,int *next, int s){    int status[V];    int u, v;    //initialization    for(u = 0; u<n; u++){       status[u] = 1;//unconsidered vertex       dist[u] = costMat[u][s];//distance from source       next[u] = s;    }    //for source vertex    status[s] = 2; dist[s] = 0; next[s] = -1;//-1 for starting vertex    while((u = minimum(status, dist, n)) > -1){       status[u] = 2;//now considered       for(v = 0; v<n; v++)          if(status[v] == 1)             if(dist[v] > dist[u] + costMat[u][v]){       dist[v] = dist[u] + costMat[u][v];//update distance       next[v] = u;       }    } } main(){    int dis[V], next[V], i, start = 0;    dijkstra(V, dis, next, start);    for(i = 0; i<V; i++)       if(i != start)          cout << start << " to " << i <<", Using: " << next[i] << ", Cost: " << dis[i] << endl; }

Output

0 to 1, Using: 0, Cost: 3 0 to 2, Using: 1, Cost: 5 0 to 3, Using: 1, Cost: 4 0 to 4, Using: 3, Cost: 6 0 to 5, Using: 2, Cost: 7 0 to 6, Using: 4, Cost: 7