Self Crossing in C++

Suppose we have an array x of n numbers. We start at point (0,0) and moves x[0] units to the north direction, then x[1] units to the west direction, x[2] units to the south direction , x[3] units to the east direction and so on. In other words, after each move our direction changes counter-clockwise. We have to devise an one-pass algorithm with O(1) extra space to determine whether our path crosses itself, or not.

So if the array is like − [3,4,2,5]

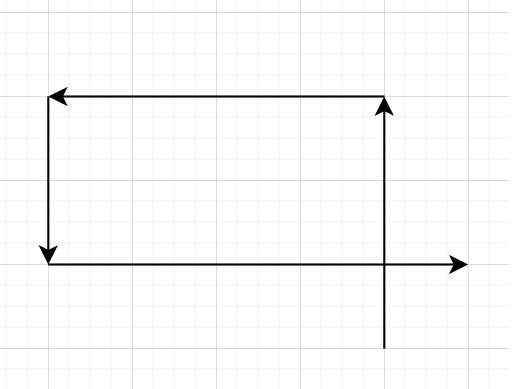
Answer will be true.

To solve this, we will follow these steps −

• insert 0 at the index 4 of x

• n := size of x, i := 4

• for not initializing anything when i < n and x[i] > x[i - 2], increase i by 1 do −

  • Do nothing

• if i is same as n, then, return false

• if x[i] >= x[i - 2] - x[i - 4], then,

  • x[i - 1] = x[i - 1] - x[i - 3]

• for increase i by 1, when i < n and x[i] < x[i - 2], increase i by 1 do −

  • Do nothing

• return true when i is not same as n

Example

Let us see the following implementation to get better understanding −

 Live Demo

#include <bits/stdc++.h> using namespace std; class Solution {    public:    bool isSelfCrossing(vector<int>& x) {       x.insert(x.begin(), 4, 0);       int n = x.size();       int i = 4;       for(; i < n && x[i] > x[ i - 2];i++);       if(i == n) return false;       if (x[i] >= x[i - 2] - x[i - 4]){          x[i - 1] -= x[i - 3];       }       for (i++; i < n && x[i] < x[i - 2]; i++);       return i != n;    } }; main(){    Solution ob;    vector<int> v = {3,4,2,5};    cout << (ob.isSelfCrossing(v)); }

Input

{3,4,2,5}

Output

1