Python Program for nth Catalan Number

In this article, we will learn about calculating the nth Catalan number.

Catalan numbers are a sequence of natural numbers that are defined by the recursive formula −

$$C_{0}= 1\:and\:C_{n+1}=\displaystyle\sum\limits_{i=0}^n C_{i}C_{n-i} for \:n\geq0;$$

The first few Catalan numbers for n = 0, 1, 2, 3, … are 1, 1, 2, 5, 14, 42, 132,429,...................

Catalan numbers can be obtained both by recursion and dynamic programming. So let’s see their implementation.

Approach 1: Recursion Method

Example

 Live Demo

# A recursive solution def catalan(n):    #negative value    if n <=1 :       return 1    # Catalan(n) = catalan(i)*catalan(n-i-1)    res = 0    for i in range(n):       res += catalan(i) * catalan(n-i-1)    return res # main for i in range(6):    print (catalan(i))

Output

1 1 2 5 14 42

The scope of all the variables and recursive calls are shown below.

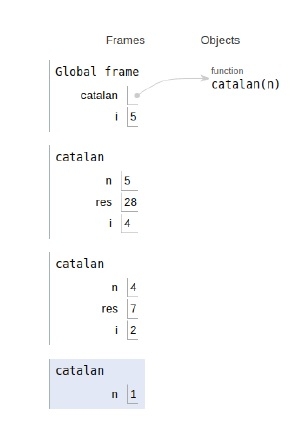
Approach 2: Dynamic Programming Method

Example

 Live Demo

# using dynamic programming def catalan(n):    if (n == 0 or n == 1):       return 1    # divide table    catalan = [0 for i in range(n + 1)]    # Initialization    catalan[0] = 1    catalan[1] = 1    # recursion    for i in range(2, n + 1):       catalan[i] = 0       for j in range(i):          catalan[i] = catalan[i] + catalan[j] * catalan[i-j-1]    return catalan[n] # main for i in range (6):    print (catalan(i),end=" ")

Output

1 1 2 5 14 42

The scope of all the variables and recursive calls are shown below.

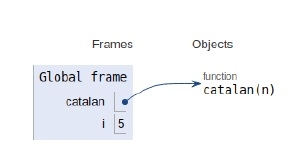
Conclusion

In this article, we learned about the method of generating the nth Catalan number.