Program to find out the length between two cities in shortcuts in Python

Suppose there are n number of cities and the cities are connected with two types of roads; highways and shortcuts. Now, there is a map and only the highways are present on the map and all the shortcuts are absent. The transport division of the cities wants to launch a transport that connects the cities utilizing the highways and the shortcuts. We know there is a shortcut between the two cities when there is no highway between them. Our task here is to find the minimum distances in terms of shortcuts from a starting city to all other cities.

So, if the input is like

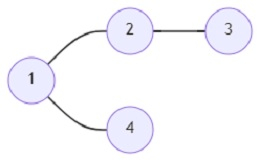
and start vertex (s) is 1, then the output will be 3 1 2.

If we only take shortcuts, the path between cities 1 and 2 will be 1->3->4->2, and the cost will be 3.

Similarly,

1 and 3: 1->3, cost 1.

1 and 4: 1->3->4, cost 2.

To solve this, we will follow these steps −

• graph := a new list containing n sets
• for each pair (x, y) in edges, do
  • x := x - 1
  • y := y - 1
  • insert y into graph[x]
  • insert x into graph[y]
• temp_arr := a new array of size n containing value -1
• b_set := a new map containing the key s - 1
• f := a new set containing set difference between numbers 0 to n and b_set
• index := 0
• while size of b_set > 0, do
  • for each element a in b_set, do
    • temp_arr[a] := index
  • nxt := a new map containing values of graph that are not subset of b_set
  • f := set difference of f and nxt
  • b_set := nxt
  • index := index + 1
• return non-zero values of temp_arr

Example

Let us see the following implementation to get better understanding −

def solve(n, edges, s):     graph = [set() for i in range(n)]     for (x, y) in edges:         x -= 1         y -= 1         graph[x].add(y)         graph[y].add(x)     temp_arr = [-1] * n     b_set = {s - 1}     f = set(range(n)).difference(b_set)     index = 0     while len(b_set) > 0:         for a in b_set:             temp_arr[a] = index         nxt = {f for f in f if not b_set.issubset(graph[f])}         f = f.difference(nxt)         b_set = nxt         index += 1     return (' '.join(str(t) for t in temp_arr if t > 0))     print(solve(4, [(1, 2), (2, 3), (1, 4)], 1)) 

Input

4, [(1, 2), (2, 3), (1, 4)], 1

Output

3 1 2