Optimal Binary Search Trees in Data Structures

A set of integers are given in the sorted order and another array freq to frequency count. Our task is to create a binary search tree with those data to find minimum cost for all searches.

An auxiliary array cost[n, n] is created to solve and store the solution of sub problems. Cost matrix will hold the data to solve the problem in bottom up manner.

Input − The key values as node and the frequency.

Keys = {10, 12, 20} Frequency = {34, 8, 50}

Output − The minimum cost is 142.

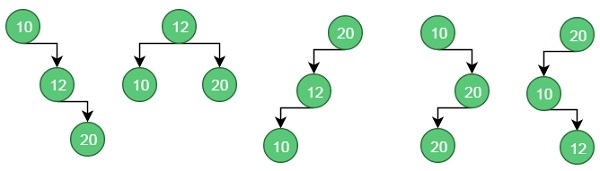
These are possible BST from the given values.

For case 1, the cost is: (34*1) + (8*2) + (50*3) = 200

For case 2, the cost is: (8*1) + (34*2) + (50*2) = 176.

Similarly, for case 5, the cost is: (50*1) + (34 * 2) + (8 * 3) = 142 (Minimum)

Algorithm

optCostBst(keys, freq, n) Input: Keys to insert in BST, frequency for each keys, number of keys. Output: Minimum cost to make optimal BST. Begin    define cost matrix of size n x n    for i in range 0 to n-1, do       cost[i, i] := freq[i]    done    for length in range 2 to n, do       for i in range 0 to (n-length+1), do          j := i + length – 1          cost[i, j] := ∞          for r in range i to j, done             if r > i, then                c := cost[i, r-1]             else                c := 0             if r < j, then                c := c + cost[r+1, j]             c := c + sum of frequency from i to j             if c < cost[i, j], then                cost[i, j] := c          done       done    done    return cost[0, n-1] End

Example

#include <iostream> using namespace std; int sum(int freq[], int low, int high){ //sum of frequency from low to high range    int sum = 0;    for (int k = low; k <=high; k++)       sum += freq[k];    return sum; } int minCostBST(int keys[], int freq[], int n){    int cost[n][n];    for (int i = 0; i < n; i++) //when only one key, move along diagonal elements       cost[i][i] = freq[i];    for (int length=2; length<=n; length++){       for (int i=0; i<=n-length+1; i++){ //from 0th row to n-length+1 row as i          int j = i+length-1;          cost[i][j] = INT_MAX; //initially store to infinity          for (int r=i; r<=j; r++){             //find cost when r is root of subtree             int c = ((r > i)?cost[i][r-1]:0)+((r < j)?cost[r+1][j]:0)+sum(freq, i, j);             if (c < cost[i][j])                cost[i][j] = c;          }       }    }    return cost[0][n-1]; } int main(){    int keys[] = {10, 12, 20};    int freq[] = {34, 8, 50};    int n = 3;    cout << "Cost of Optimal BST is: "<< minCostBST(keys, freq, n); }

Output

Cost of Optimal BST is: 142