C++ Queries for DFS of a Subtree in a Tree

In this problem we are given a binary tree and we are required to perform dfs from a particular node in which we assume the given node as the root and perform dfs from it.

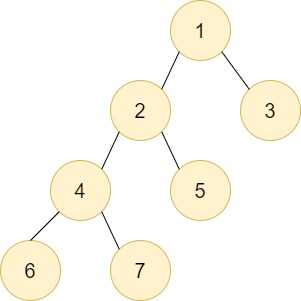
In the above tree suppose we are required to perform DFS from node F

In this tutorial we are going to apply some unorthodox methods so that it will decrease our time complexity substantially and thus we will be able to run this code for higher constraints also.

Approach − In this approach we are not simply going to go the naive way i.e. where we simply apply dfs for every node as it will not work for higher constraints so we try to use some unorthodox methods to avoid getting TLE.

 #include <bits/stdc++.h> using namespace std; #define N 100000 // Adjacency list to store the // tree nodes connections vector<int> v[N]; unordered_map<int, int> mape; // will be used for associating the node with it's index vector<int> a; void dfs(int nodesunder[], int child, int parent){ // function for dfs and     precalculation our nodesunder     a.push_back(child); // storing the dfs of our tree     // nodesunder of child subtree     nodesunder[child] = 1;     for (auto it : v[child]) { // performing normal dfs         if (it != parent) { // as we the child can climb up to         //it's parent so we are trying to avoid that as it will become a cycle             dfs(nodesunder, it, child); // recursive call             nodesunder[child] += nodesunder[it]; // storing incrementing the nodesunder         //by the number of nodes under it's children         }     } } // Function to print the DFS of subtree of node void printDFS(int node, int nodesunder[]){     int ind = mape[node]; // index of our node in the dfs array     cout << "The DFS of subtree " << node << ": ";     // print the DFS of subtree     for (int i = ind; i < ind + nodesunder[node]; i++){ // going through dfs array and then     //printing all the nodes under our given node         cout << a[i] << " ";     }     cout << endl; } void addEdgetoGraph(int x, int y){ // for maintaining adjacency list     v[x].push_back(y);     v[y].push_back(x); } void mark(){ // marking each node with it's index in dfs array     int size = a.size();     // marks the index     for (int i = 0; i < size; i++) {        mape[a[i]] = i;     } } int main(){     int n = 7;     // add edges of a tree     addEdgetoGraph(1, 2);     addEdgetoGraph(1, 3);     addEdgetoGraph(2, 4);     addEdgetoGraph(2, 5);     addEdgetoGraph(4, 6);     addEdgetoGraph(4, 7);     // array to store the nodes present under of subtree     // of every node in a tree     int nodesunder[n + 1];     dfs(nodesunder, 1, 0); // generating our nodesunder array     mark(); // marking the indices in map     // Query 1     printDFS(2, nodesunder);     // Query 2     printDFS(4, nodesunder);     return 0; }

Output

The DFS of subtree 2: 2 4 6 7 5 The DFS of subtree 4: 4 6 7

Understanding the code

In this approach we are precalculating the order of dfs and storing it in a vector now when we have precalculated the dfs we also calculate the nodes present under each subtree starting from each node and then we simply traverse form the starting index of then node to all the number of nodes present inside it’s subtree.

Conclusion

In this tutorial, we solve a problem to solve the Queries for DFS of a subtree in a tree. We also learned C++ program for this problem and the complete approach ( Normal) by which we solved this problem.

We can write the same program in other languages such as C, java, python and other languages. Hope you find this article helpful.