C++ Program to Check Whether Graph is DAG

DAG stands for Directed Acyclic Graph. It is a special type of graph where all edges are directed and there are no cyclic connections of edges. In this article, we will discuss how to check whether a graph is a DAG using Kahn's algorithm (BFS based topological sorting).

What is DAG?

A DAG is a directed graph with no cycles. That means in this type graph it is not possible to start from any node and follow a sequence of edges such that you will return back to the starting node. DAGs are commonly used in applications like task scheduling, build systems, and data processing pipelines. Technically a graph is called a DAG, if:

• It is a directed graph.
• There is not even a single cycle present in the graph.
• It is possible to perform topological sorting on the graph.

The image below shows an example of a DAG.

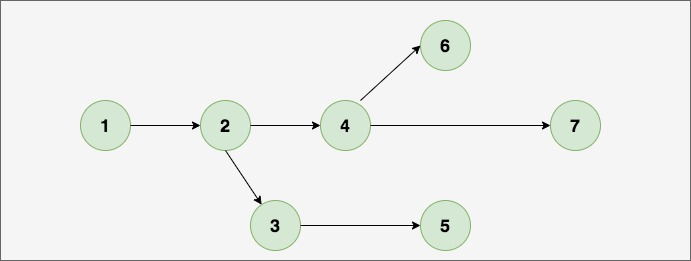
Check Whether a Graph is DAG

To check whether a directed graph is a DAG, we can perform topological sorting using BFS-based Kahn's algorithm. If we are able to visit all vertices by this method, then the graph is a DAG. Otherwise, it contains a cycle and hence is not a DAG.

Steps to Check DAG using Topological Sort

The following steps explain the logic used to check whether a graph is a DAG:

• Step 1: Initialize an array to keep track of the in-degree of each vertex.
• Step 2: Calculate the in-degree for all vertices by scanning the adjacency list.
• Step 3: Insert all vertices with in-degree 0 into a queue.
• Step 4: Start a loop to remove vertices from the queue and decrease the in-degree of their neighbours.
• Step 5: If we are able to visit all vertices, the graph is a DAG. Otherwise, it has a cycle.

Note: The in-degree of a vertex is the number of edges coming into that vertex.

C++ Program to Check Whether Graph is DAG

The code below implements above algorithm in C++ language. It creates a directed graph and checks whether it is a DAG or not.

#include <iostream> #include <vector> #include <queue> using namespace std; bool isDAG(int V, vector<vector<int>>& adj) { vector<int> indegree(V, 0); for (int u = 0; u < V; u++) { for (int v : adj[u]) { indegree[v]++; } } queue<int> q; for (int i = 0; i < V; i++) { if (indegree[i] == 0) q.push(i); } int count = 0; while (!q.empty()) { int node = q.front(); q.pop(); count++; for (int neighbor : adj[node]) { indegree[neighbor]--; if (indegree[neighbor] == 0) q.push(neighbor); } } return (count == V); } int main() { int V = 6; vector<vector<int>> adj(V); // Example DAG adj[5].push_back(2); adj[5].push_back(0); adj[4].push_back(0); adj[4].push_back(1); adj[2].push_back(3); adj[3].push_back(1); if (isDAG(V, adj)) { cout << "The graph is a DAG." << endl; } else { cout << "The graph is NOT a DAG (it contains a cycle)." << endl; } return 0; } 

The output of the above code will be:

The graph is a DAG.