Construct Pushdown automata for L = {0n1m2(n+m) | m,n = 0} in C++

We are given with a language “L” and the task is to construct a pushdown automata for the given language which explains that the occurrences of 2’s will be the addition of occurrences of 0’s and 1’s and also, occurrence of 0 and 1 will be minimum one which can also makes the string NULL and it should be accepted by the automata.

What is pushdown Automata?

A pushdown automata or pushdown automaton or PDA is a technique to implement a context−free grammar in a similar way we design Deterministic Finite Automaton or DFA for a regular grammar. A DFA can operate on finite data, but a PDA can operate on infinite data. We can understand pushdown automata as the combination of “finite state machine” and a “stack”.

A pushdown automaton has three components −

• an input tape,

• a control unit, and

• a stack with infinite size.

A PDA can be formally described as a 7-tuple (Q, Σ, S, δ, q0, I, F) −

• Q is the finite number of states

• Σ is input alphabet

• S is stack symbols

• δ is the transition function: Q × (Σ υ {ε}) × S × Q × S*

• q0 is the initial state (q0 Ε Q)

• I is the initial stack top symbol (I Ε S)

• F is a set of accepting states (F Ε Q)

Let’s construct a pushdown Automata for the given language −

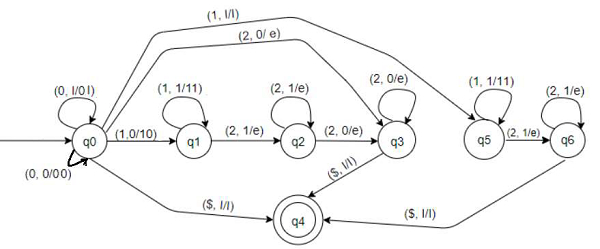
The strings that are acceptable by this PDA are of the form −

• 0ⁿ2ⁿ − 02, 0022, 000222 etc. No. of 0s is equal to no. of 2s. When m is 0 we will have no 1s. Keep pushing 0s and as soon as the first 2 is encountered then pop 0s. If we reach the end of the string and are left with no 0s then the string is accepted.

• 1^m2^m − 12, 1122, 111222 etc. No. of 1s is equal to no. of 2s. When n is 0 we will have no 0s. Keep pushing 1s and as soon as the first 2 is encountered then pop 1s. If we reach the end of the string and are left with no 1s then the string is accepted.

• 0ⁿ1^m2^m+n − 0122, 001112, 001112 etc. No. of 2s is equal to sum of no. of 0s and 1s. Keep pushing 0s and 1s. As soon as the first 2 is encountered then pop 1s and 0s If we reach the end and no 0 is left then the string is accepted.

• NULL string is also accepted. 0⁰1⁰2⁰.

Let’s understand the machine

• Transitions for state q0

  −

  • ( 0, I/0I ) − If top of stack is I and current input symbol is 0 then push 0 to top of stack and remain at q0. Stack becomes 0I...

  • ( 0, 0/00 ) − If top of stack is 0 and current input symbol is also 0 then push 0 to top of stack and remain at q0. Stack becomes 00.... Keep pushing 0s until the next 1 or 2.

  • ( 1, 0/10 ) − If top of stack is 0 and current input symbol is 1 then push 1 to top of stack and move to q1. Stack becomes 10...

  • ( 1, I/I ) − If top of stack is I and current input symbol is 1 then do nothing and move to q5.

  • ( 2, 0/e ) − If top of stack is 0 and current input symbol is 2 then pop 0 and move to q3.

  • ( $, I/I ) − If top of stack is I and there is no input then do nothing and move to q4. For NULL string.

• Transitions for state q1

  −

  • ( 1, 1/11 ) − If top of stack is 1 and current input symbol is also 1 then push 1 to top of stack and remain at q1. Stack becomes 11.... Keep pushing 1s until the next 2.

  • ( 2, 1/e ) − If top of stack is 1 and current input symbol is 2 then pop 1 and move to q2.

• Transitions for state q2

  &minus

  • ( 2, 1/e ) − If top of stack is 1 and current input symbol is 2 then pop 1 and remain at q2.

  • ( 2, 0/e ) − If top of stack is 1 and current input symbol is 2 then pop 1 and move to q3.

• Transitions for state q3

  −

  • ( 2, 0/e ) − If top of stack is 1 and current input symbol is 2 then pop 1 and move to q4.

  • ( $, I/I ) − If top of stack is I and there is no input then do nothing and move to q4. For NULL string.

• Transitions for state q5

  −

  • ( 1, 1/11 ) − If top of stack is 1 and current input symbol is also 1 then push 1 to top of stack and remain at q5. Stack becomes 11.... Keep pushing 1s until the next 2.

  • ( 2, 1/e ) − If top of stack is 1 and current input symbol is 2 then pop 1 and move to q6.

• Transitions for state q6

  −

  • ( 2, 1/e ) − If top of stack is 1 and current input symbol is 2 then pop 1 and remain at q6.

  • ( $, I/I ) − If top of stack is I and there is no input then do nothing and move to q4. For NULL string.