
 Data Structure
Data Structure Networking
Networking RDBMS
RDBMS Operating System
Operating System Java
Java MS Excel
MS Excel iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C Programming
C Programming C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Can we convert a non-deterministic finite automata into a deterministic finite Automata?
Yes, we can convert a NFA into DFA. For every NFA there exists an equivalent DFA. The equivalence is defined in terms of languages acceptance. Since NFA is nothing but a finite automata in which zero, one or more transitions on an input symbols are permitted. It can always construct finite automata which will simulate all moves of DFA on a particular input symbol in parallel, then get a finite automata in which there will be exactly one transition on every input symbol. Here, corresponding to a NFA there exist a DFA. To construct DFA equivalent to NFA, it should be remembered that states of DFA are a collection of states of NFA.
Algorithm NFA – to – DFA
Input − NFA with set of states N = {n0,n1……nn}, with start state n0.
Output − DFA, with set of states D′={d0,d1,d2……dn}, with start state d0.
d0=ε−closure (n0)
D′={d0}
set d0 unmarked
while there is an unmarked state d in D′. { set d marked { For each input symbol 'a' { Let T be a set of states in NFA to which there is a transition on 'a' from some state ni in d d′=ε−closure (T). If d′ is not already present in D′ { D′=D′∪{d′} Add transition d→d′,labeled 'a' set d′ unmarked } } } } Example − Design Lexical Analyzer for the following LEX Program.
AUXILIARY DEFINITION S letter = A|B|C|…….|Z digit = 0 |1|2|………|9 TRANSLATION RULES begin {return 1} end {return 2} If {return 3} then {return 4} else {return 5} letter (letter+digit)* {value=Install ( );return 6} digit + {value=Install ( );return 7} < {value=1;return 8} <= {value=2;return 8} = {value=3;return 8} < > {value=4;return 8} > {value=5;return 8} >= {value=6;return 8} Solution
- The combined NFA for various patterns will be
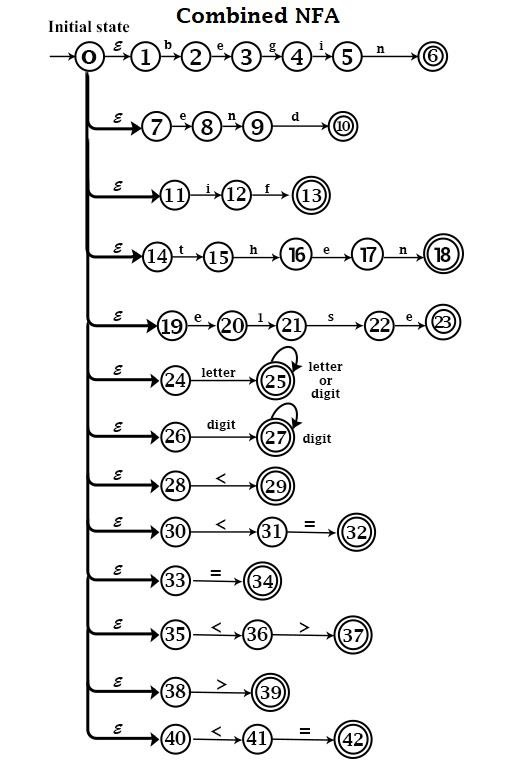
- Convert NFA to DFA − The corresponding DFA will be.
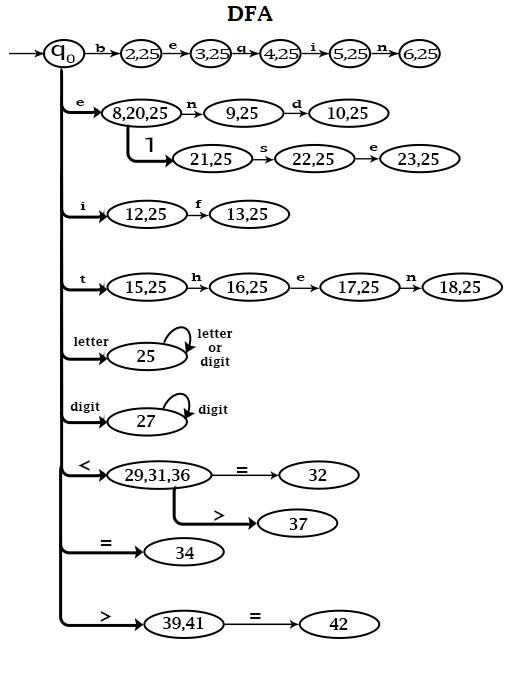
States {0, 1, 7, 11, 14, 19, 24, 26, 28, 30, 33, 35, 38, 40} are combined and named as q0to make a starting state of DFA.
In combined NFA, transitions from state 1 to 2 and from state 24 to 25 are the same because Input 'b' is a letter.
States 2, 25 are combined. Similarly, other states are combined.
States 29, 31 & 36 are combined because they all reach after getting the input '<'.
Similarly, other states are combined.

