C program for DFA accepting all strings over w ∈(a,b)* containing “aba” as a substring

Problem

Design a DFA for the language L={w1abaw2 | w1,w2 ?(a,b)*}, which means the DFA accepts all strings which contain “aba” as a substring.

Solution

The strings that are accepted by language L= {aba,aabaa, aabab, babab, ababa, …….}

Step 1 − Transition diagram for minimal string (starting string) −

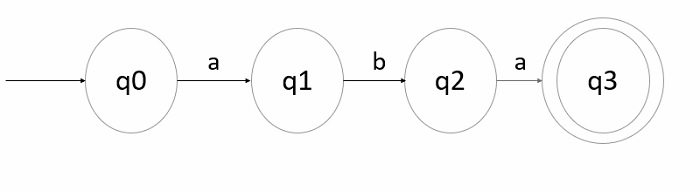
If w1 and w2 are null then the string it generates is “aba” because w1, w2 ε(a,b)*

q0 is the initial state and q3 is the final state.

Step 2 − The final DFA for the given language is as follows −

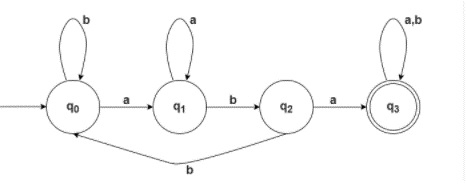
Explanation

• qo is the initial state q0 on ‘a’ goes to q1 and on ‘b’ goes to q0, according to DFA each state has to generate a transition on both inputs.

• q1 on ‘a’ goes to q1 and on ‘b’ goes to q2, we have to keep in mind according to the given language we need to generate a substring “aba”.

• q2 on ‘a’ goes on q3 on ‘b’ goes to q0 state.

• q3 which is the final state, on input ‘a’ and ‘b’ goes to q3 only.

Transition Table

Let’s see the transition table as follows −

Current state	Input a	Input b
q0	q1	q0
q1	q1	q2
q2	q3	q0
*q3	q3	q3

Example

Following is the C program for construction of DFA accepting all strings over w ε(a,b)* which contains “aba” as a substring -

 Live Demo

#include <stdio.h> #include <string.h> void checkDFA(char s[] ) {    // storing initial state    int initialState = 0;    //assign initial state to previous state.    int previousState = initialState;    int finalState;    for(int i = 0; i < strlen(s); i++)    {       if((previousState == 0 && s[i] == 'a') || (previousState == 1 && s[i] == 'a')) {          finalState = 1;       }       if((previousState == 0 && s[i] == 'b') || (previousState == 2 && s[i] == 'b')) {          finalState = 0;       }       if(previousState == 1 && s[i] == 'b') {          finalState = 2;       }       if((previousState == 2 && s[i] == 'a') || (previousState == 3)) {          finalState = 3;       }       previousState = finalState;    }    if(finalState == 3) {       printf("given string is Accepted");    }    else    {       printf("given string is Not Accepted");    } } int main() {    // Given string    char s[40];    printf("implementation of DFA which having a sub string 'aba':
 enter a string:");    scanf("%s",s);    checkDFA(s);    return 0; }

Output

The output is as follows −

Run 1: implementation of DFA which having a sub string 'aba': enter a string:aba given string is Accepted. Run 2: implementation of DFA which having a sub string 'aba': enter a string:abba given string is Not Accepted.