Area of the Largest Triangle inscribed in a Hexagon in C++

In this problem, our task is to find the area of the largest triangle that can be inscribed in a regular hexagon. Each side of the hexagon and triangle is of length a and b, respectively.

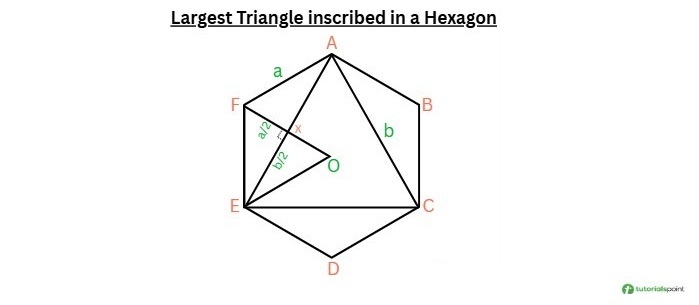
Area of the Largest Triangle Inscribed in a Hexagon

You can calculate the area of the largest triangle inscribed in a regular hexagon using the following formula:

$$ Area\ of\ triangle\ inside\ hexagon\ = \frac{3\sqrt{3}}{4} \cdot a^2 $$

Derivation

The first step is to establish a relation between a and b, as the value of a(side of the hexagon) is given.

In triangle EXF, EF2 = FX2 + XE2 (Using Pythagorean theorem) => a2 = (a/2)2 + (b/2)2 (X is perpendicular bisector of AE and OF) => b = a * sqrt(3) 

Now, we need the height of the triangle AEC.

Height of equilateral triangle = (b * sqrt(3)) / 2 

Calculating the area of the triangle (AEC) inscribed inside a hexagon:

Area of triangle = (1/2) * base * height Area = (1/2) * b * ((b * sqrt(3)) / 2) Substituting b = a * sqrt(3): Area = (1/2) * (a * sqrt(3)) * ((a * sqrt(3)) / 2) Area = (3 * sqrt(3) / 4) * a^2 

Let's see some input-output scenarios for a better understanding:

Scenario 1

Input: a = 6 Output: Area = 46.765 Explanation: Using the formula: Area = (3 * sqrt(3) / 4) * a^2 Area = (3 * sqrt(3) / 4) * 6^2 Area = (3 * 1.732 / 4) * 36 Area = 46.765 

Scenario 2

Input: a = 10 Output: Area = 129.903 Explanation: Area = (3 * sqrt(3) / 4) * 10^2 Area = (3 * 1.732 / 4) * 100 Area = 129.903 

C++ Program for Area of Largest Triangle in Hexagon

To calculate the area of the Largest Triangle inscribed in a Hexagon using a C++ program, we just need to implement the above-discussed formula as shown below:

#include <iostream> #include <cmath> using namespace std; float maxTriangleArea(float a) { if (a < 0) // if value is negative it is invalid return -1; float area = (3 * sqrt(3) * pow(a, 2)) / 4; return area; } int main() { float a = 6; cout << "Side of hexagon is: " << a << endl; cout << "Area of largest triangle is: " << maxTriangleArea(a); } 

The output of the above code is as follows:

Side of hexagon is: 6 Area of largest triangle is: 46.7654