AVL Tree Program in C

What Is an AVL Tree?

Adelson-Velskii and Landis are the people who discovered it, so the name came from their names i.e., AVL. It is commonly referred to as a height binary tree. An AVL tree is one that has one of the following characteristics at each of its nodes.

If a node's longest path in its left subtree is longer than its longest path in its right subtree, the node is said to be "left heavy."

If the longest path in a node's right subtree is one more long than the longest path in its left subtree, the node is said to be "right heavy."

If the longest paths in the right and left subtrees are equal, a node is said to be balanced.

The AVL tree is a height-balanced tree where each node's right and left subtree height differences are either -1, 0 or 1. A factor known as the balance factor keeps the subtrees' height differences apart. As a result, we can define AVL as a balanced binary search tree in which each node's balance factor is either -1, 0 or +1. In this case, the formula follows to determine the balancing factor:

Balance factor properties -

• If a subtree has a balance factor greater than zero, it is said to be left-heavy because the height of the left subtree is greater than the height of the right subtree, implying that the left subtree contains more nodes than the right subtree.
• If a subtree has a balance factor of 0, it is said to be right-heavy because the height of the left subtree is less than the height of the right subtree, implying that the right subtree has more nodes than the left subtree.
• If the balance factor is zero, the subtree is perfectly balanced, with equal heights in both the left and right subtrees.

The AVL Tree's rotations:

If any node of the tree falls out of balance, the necessary rotations are carried out to correct the imbalance.

AVL Tree Operations in C

In the AVL tree, there are three types of operations that are performed:

• A New Node is Inserted
• Removal of a Node
  removing a node from the right subtree
  removing of a Node from the Left Subtree
• Looking for a Node in an AVL Tree

To carry out these operations, we must perform the four types of rotations. Four different rotational kinds are possible and are used under various scenarios as follows:

LL Rotation: When a new node is added as the left child of the unbalanced node's left subtree.

RR Rotation: When a new node is added as the right child of the right subtree of an unbalanced node, this process is known as RR Rotation.

LR Rotation: When a new node is added as the left child of an unbalanced node's right subtree.

RL Rotation: When a new node is added as the right child of an unbalanced node's left subtree.

Implementation:

Insertion in AVL Tree: To ensure that the given tree remains AVL after each insertion, we must add some re-balancing to the standard BST insert operation.

The two basic operations that can be used to balance a BST without violating the BST property are as follows (keys(left) < key(root) < keys(right)).

• Left Rotation
• Right Rotation

Insertion procedures include the following steps:

• Allow the newly added node to be w
• Insert the standard BST insert for w.
• Travel up from w to find the first unbalanced node. Allow z to be the first unbalanced node, y to be z's child on the path from w to z, and x to be z's grandchild on the path from w to z.
• Rebalance the tree by performing the necessary rotations on the z-rooted subtree. As x, y, and z can be arranged in four different ways, there are four possible cases that must be handled.
• The four possible arrangements are as follows:
• y is z's left child, and x is y's left child (Left Left Case)
  y is z's left child, and x is y's right child (Left Right Case)
  y is z's right child, and x is y's right child (Right Right Case)
  sy is z's right child, and x is y's left child (Right Left Case).

AVL Tree Program in C

Program 1:

Output

4 2 1 3 5 6 

Representation:

As a result, we got the above AVL tree after inserting those elements. The preorder traversal of the above AVL tree is 4->2->1->3->5->6.

Program 2:

Output

------- AVL TREE -------- 1. Insert 2. Delete 3. Search 4. Inorder 5. Preorder 6. Postorder 7. EXIT Enter Your Choice: 1 Enter data: 2 Do you want to continue? y ------- AVL TREE -------- 1. Insert 2. Delete 3. Search 4. Inorder 5. Preorder 6. Postorder 7. EXIT Enter Your Choice: 1 Enter data: 2 Do you want to continue? y ------- AVL TREE -------- 1. Insert 2. Delete 3. Search 4. Inorder 5. Preorder 6. Postorder 7. EXIT Enter Your Choice: 3 Enter data: 2 Node found Do you want to continue? y ------- AVL TREE -------- 1. Insert 2. Delete 3. Search 4. Inorder 5. Preorder 6. Postorder 7. EXIT Enter Your Choice: 2 Enter data: 2 Do you want to continue? y ------- AVL TREE -------- 1. Insert 2. Delete 3. Search 4. Inorder 5. Preorder 6. Postorder 7. EXIT Enter Your Choice: 4 2 Do you want to continue? n 

Output2: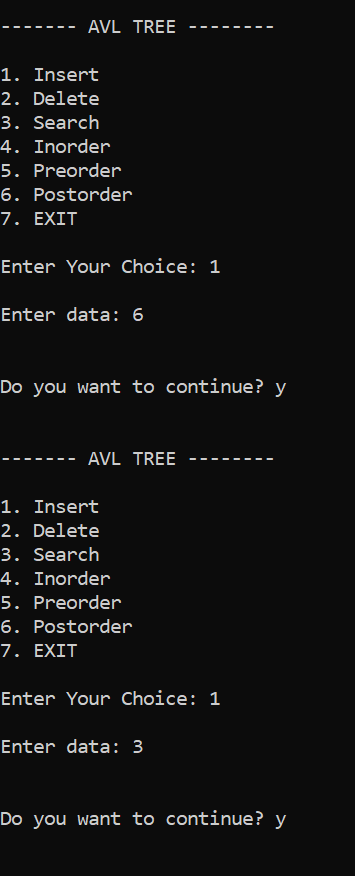

Conclusion:

The AVL tree's running time complexity for insertion operations is O(log n) for finding the place of insertion and returning to the root. Similar to this, determining the node to be deleted and carrying out the subsequent operations to change the AVL tree's balance factor have running time complexity of O(log n). Compared to the binary search tree, the AVL tree has a faster and more stable time complexity.