Downloaded 10 times
Uploaded byBla Blu Gunn
Solving for coordinates of intersection between lines
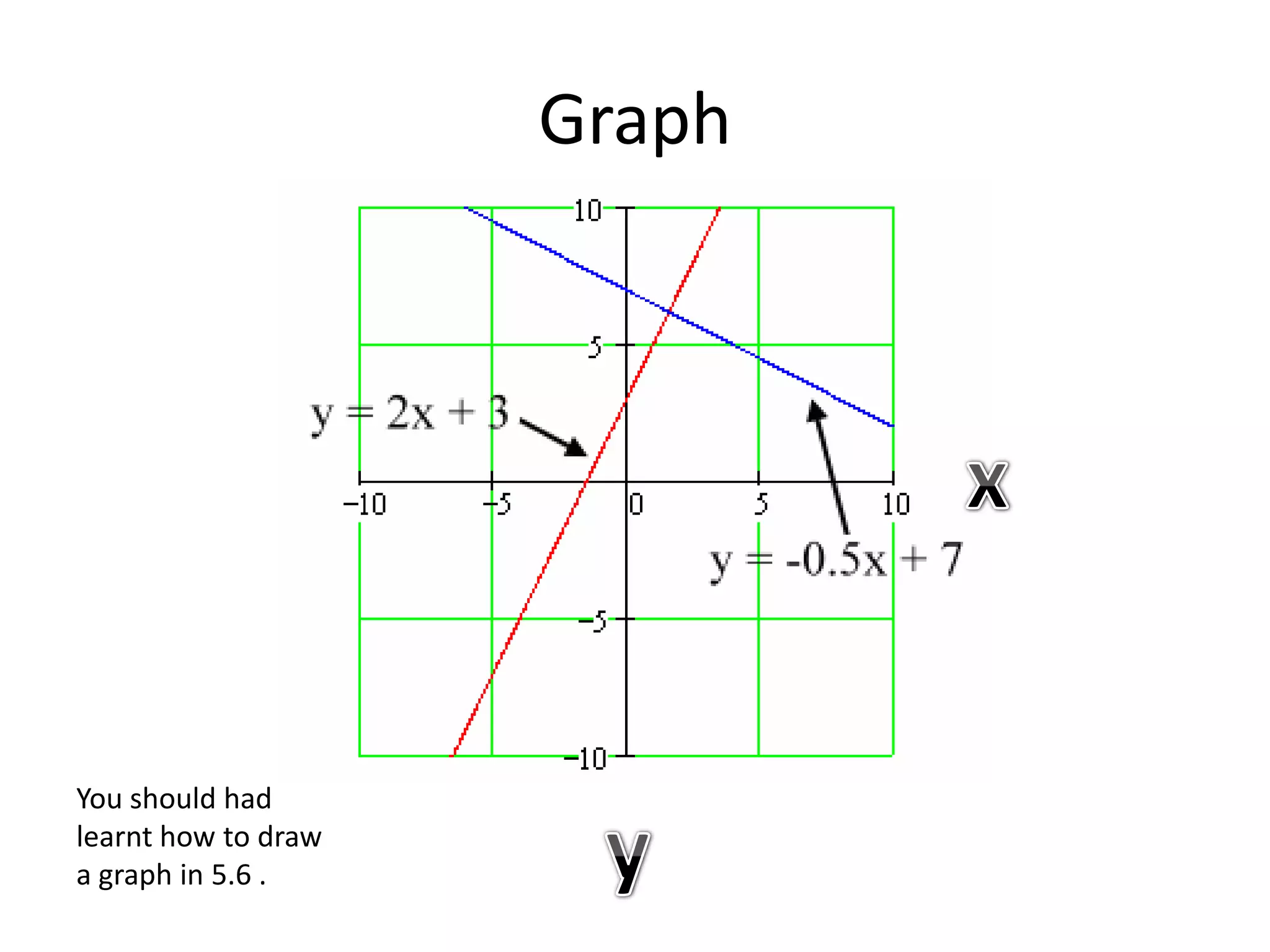
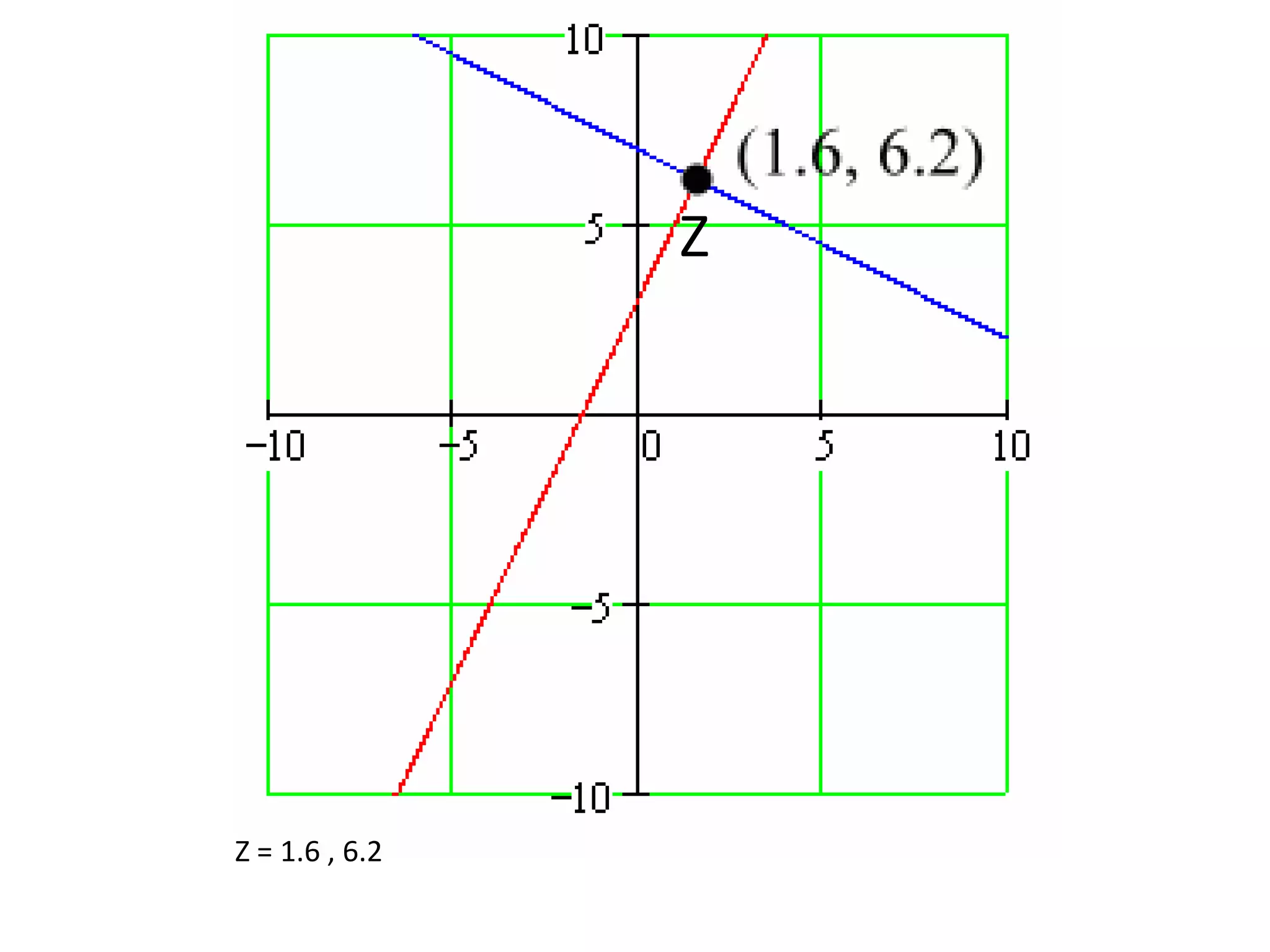
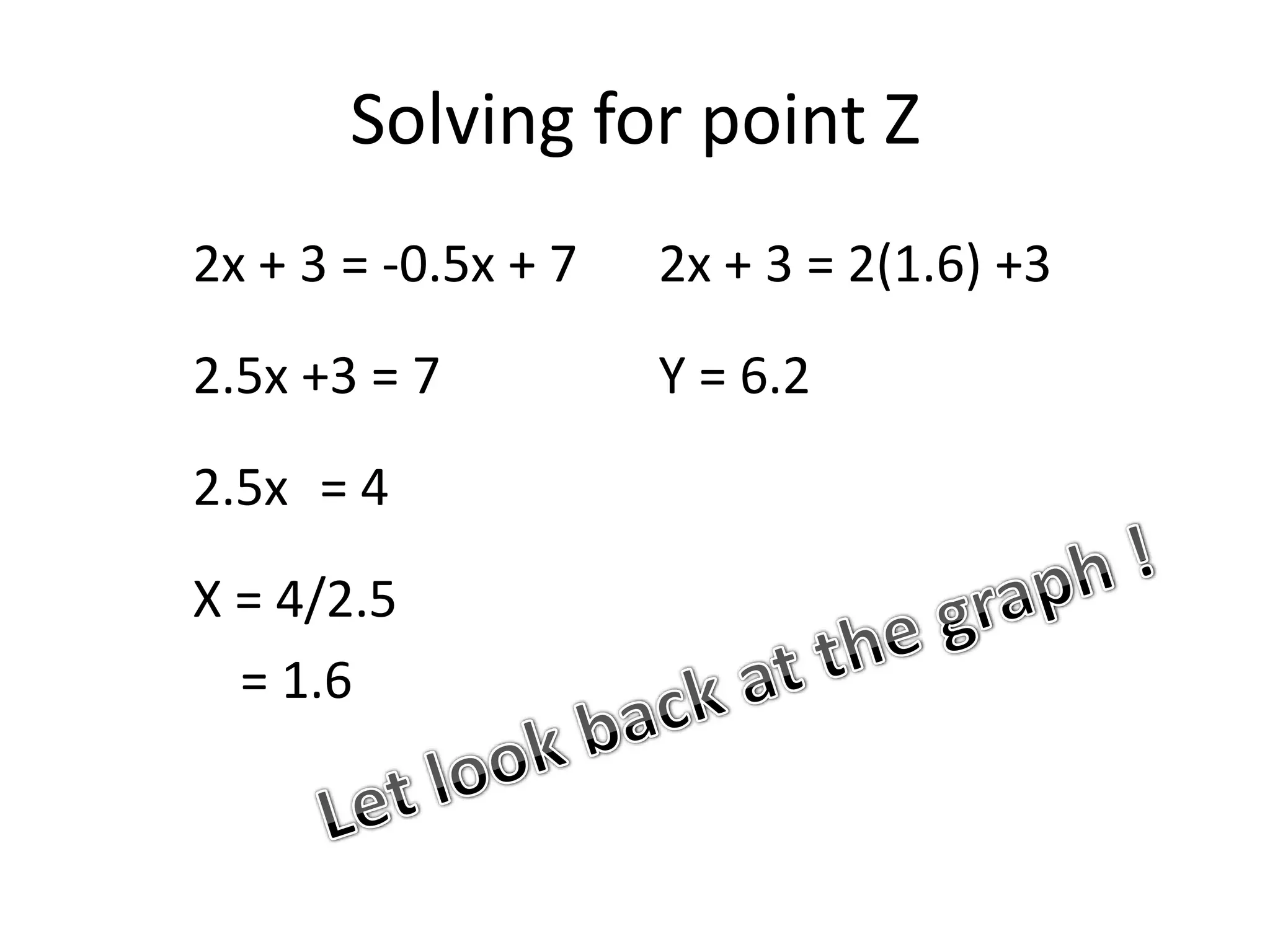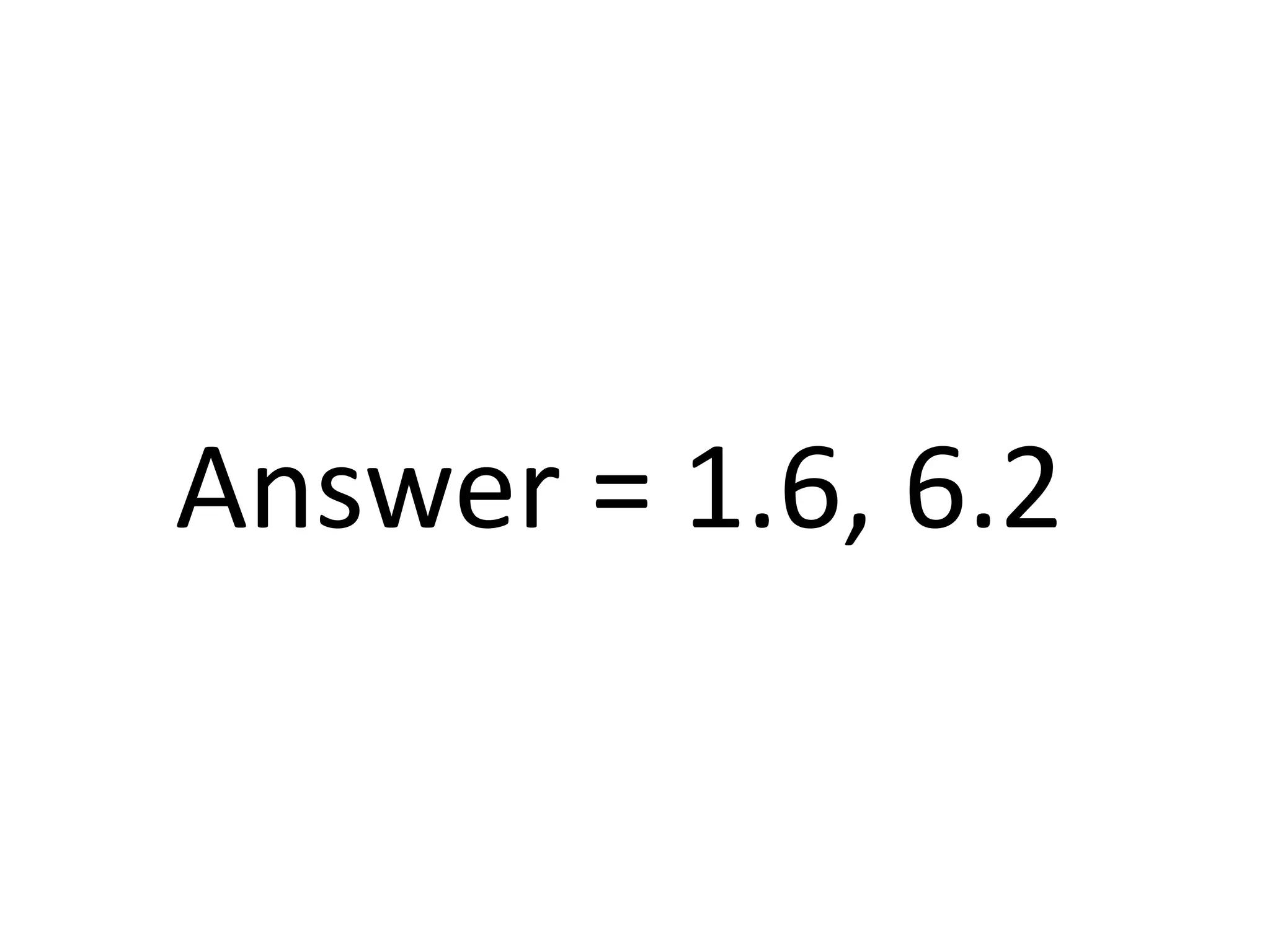This document explains how to find the intersection point of two lines by setting their equations equal to each other and solving for the shared x- and y-coordinates. It provides an example of finding the intersection point Z of the lines with equations Y = 2x + 3 and Y = -0.5x + 7. The equations are set equal to each other and solved for x = 1.6 and y = 6.2, which is verified as point Z on the graphed lines.
Solving for coordinates of intersection between lines
- 1. Solving for coordinatesof intersection between linesBy Gunn Wei Lim 2O2 (11)
- 2. What does itmean?Basically, its solving the coordinates of 2 intersecting lines to find the common point or the intersecting point where both lines intersect.Don’t understand?Let see how to solve first !
- 3. How to solveFirstlywe have to find out the equation of the 2 intersecting lines. In the equation, y will be the subject and there is a gradient and a point in which the line intersects with the y-axis. When we find the equation of both lines, we can set them as equal to each other. As there is a intersecting point, the value of x in both equation will be the same.Boring ==zzzLet’s have an example ! :D
- 4. Example We havetwo equation … Y = 2x + 3 Y = -0.5x + 7Let’s see this in a graph !
- 5. GraphxYou should hadlearnt how to draw a graph in 5.6 .y
- 6. GraphZFrom the graph,we can see that :The two equations intersect at a point which is point Z (now we must find the point Z)
- 7. When the twoequations intersect at point Z, the value of x and y in both equation will be the same
- 8. Hence we canwrite …Solving for point Z2x + 3 = -0.5x + 72.5x +3 = 72.5x = 4X = 4/2.5 = 1.62x + 3 = 2(1.6) +3 Y = 6.2Let look back at the graph !
- 9. ZZ = 1.6, 6.2
- 10.
- 11. Below is avideo that will let youunderstand gradient and intercept ! ( A recap for 5.6)