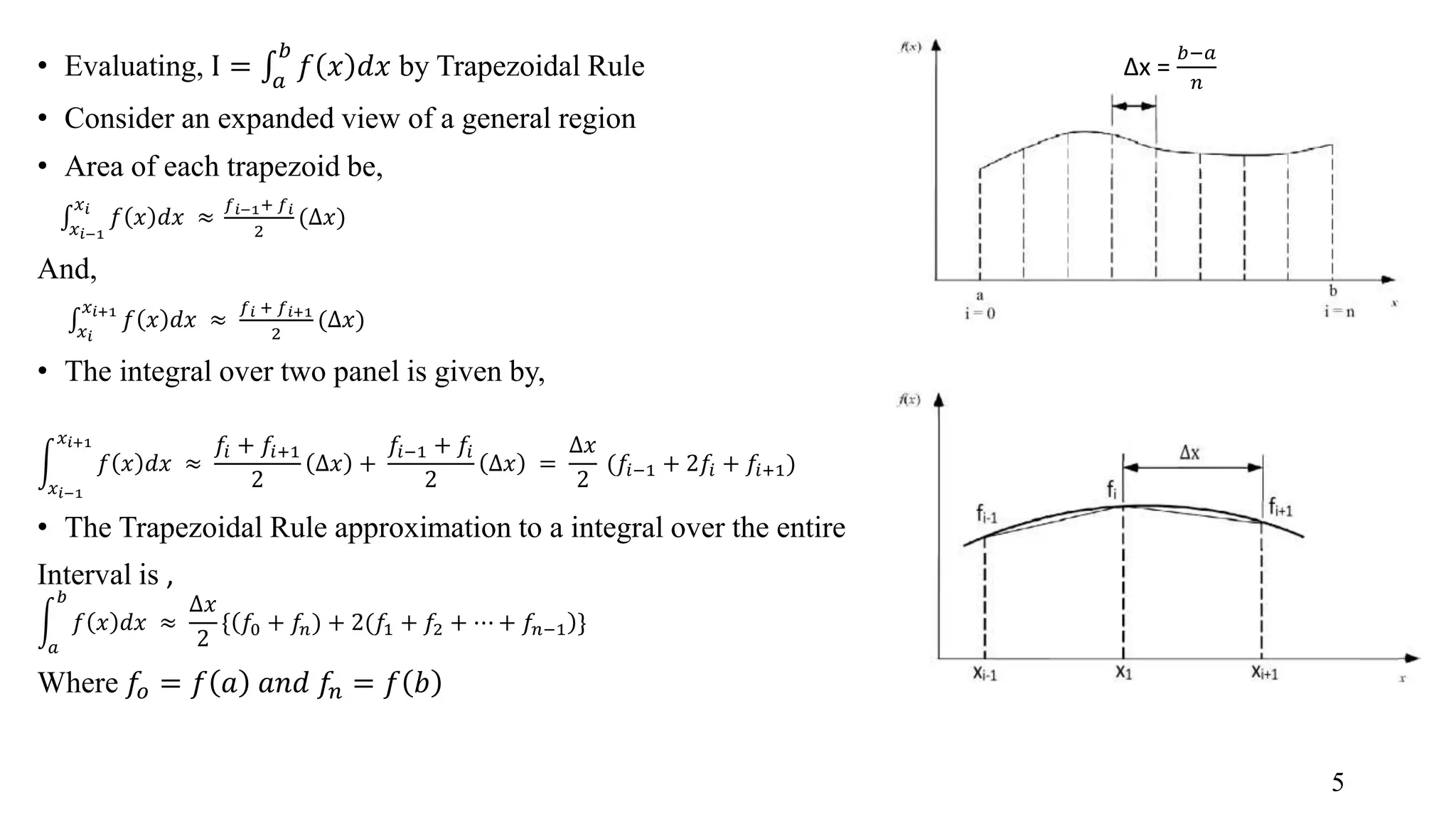
The document provides an overview of numerical integration techniques, including the trapezoidal rule, Simpson's rule, and Gaussian quadrature, highlighting their methods for approximating definite integrals. It explains how these methods differ and includes examples of their application in practical problems, such as calculating the area under curves and flow rates in streams. The conclusion indicates that while these methods provide approximations, they are essential for various engineering calculations.



![• Approximating the area of the panel by the area under the parabola is given by, 𝑥 𝑖−1 𝑥 𝑖+1 𝑓2 𝑥 𝑑𝑥 = ∆𝑥 3 [ 𝑓 𝑥𝑖−1 + 4𝑓 𝑥𝑖 + 𝑓(𝑥𝑖+1)] • The Simpson’s rule approximation to the integral over the entire interval is 𝑎 𝑏 𝑓 𝑥 𝑑𝑥 ≈ ∆𝑥 3 𝑓0 + 4𝑓1 + 2𝑓2 + 4𝑓3 + ⋯ + 2𝑓𝑛−2 + 4𝑓𝑛−1 + 𝑓𝑛 Where 𝑓𝑜 = 𝑓 𝑎 𝑎𝑛𝑑 𝑓𝑛 = 𝑓 𝑏 7](https://image.slidesharecdn.com/tausifupload-180523130720/75/Presentation-on-Numerical-Integration-7-2048.jpg)
![SIMPSON’S 3/8 RULE • Consists of taking the area under a cubic equation connecting four points. • Number of interval must be multiple of three • The formula for Simpson’s 3/8 rule is 𝑎 𝑏 𝑓 𝑥 𝑑𝑥 = 3∆𝑥 8 [ 𝑓0 + 𝑓𝑛 + 2 𝑓3 + 𝑓6 + ⋯ + 𝑓𝑛−3 +3 𝑓1 + 𝑓2 + 𝑓4 + 𝑓5 + ⋯ + 𝑓𝑛−1 ] 8](https://image.slidesharecdn.com/tausifupload-180523130720/75/Presentation-on-Numerical-Integration-8-2048.jpg)






