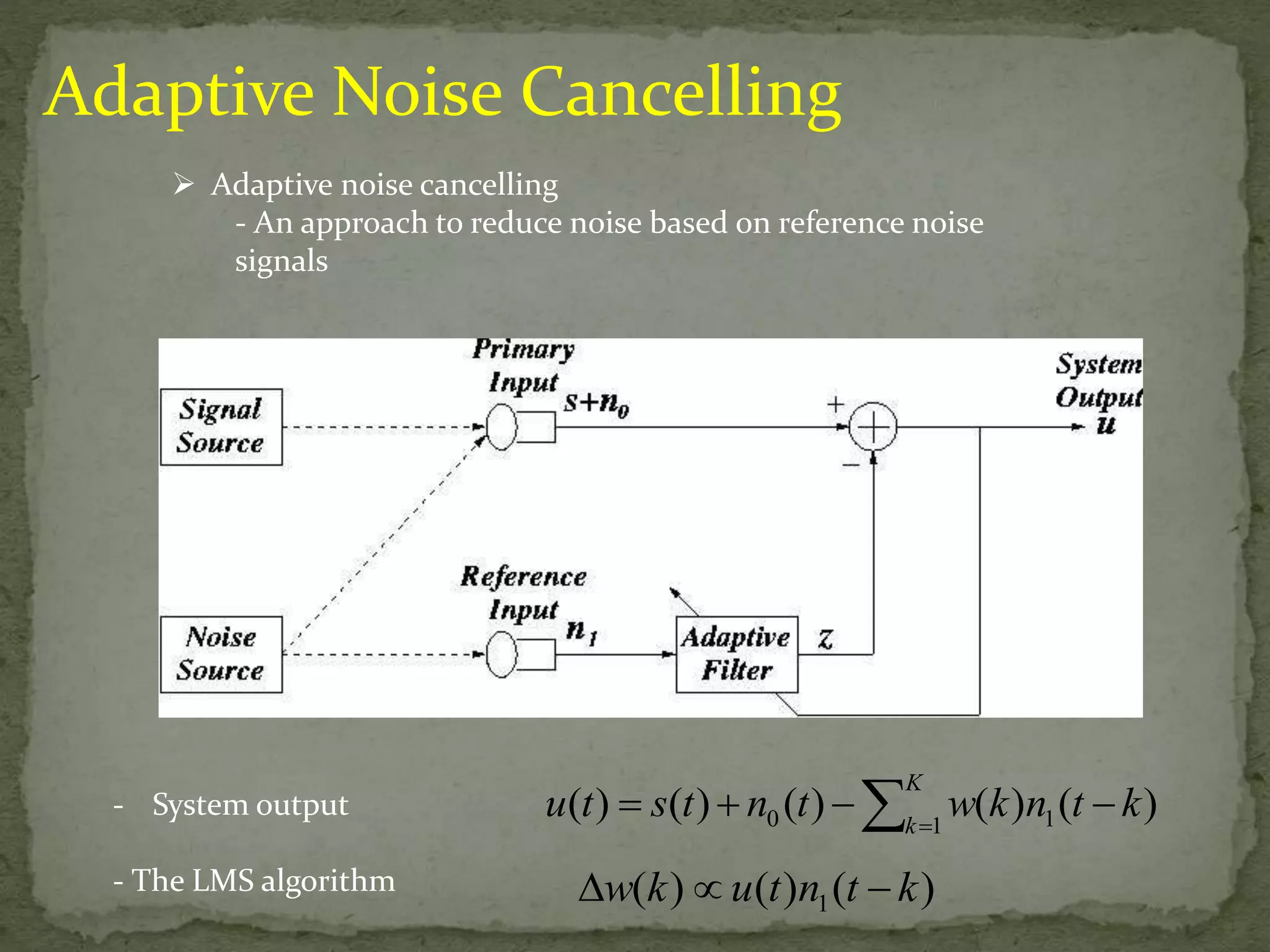
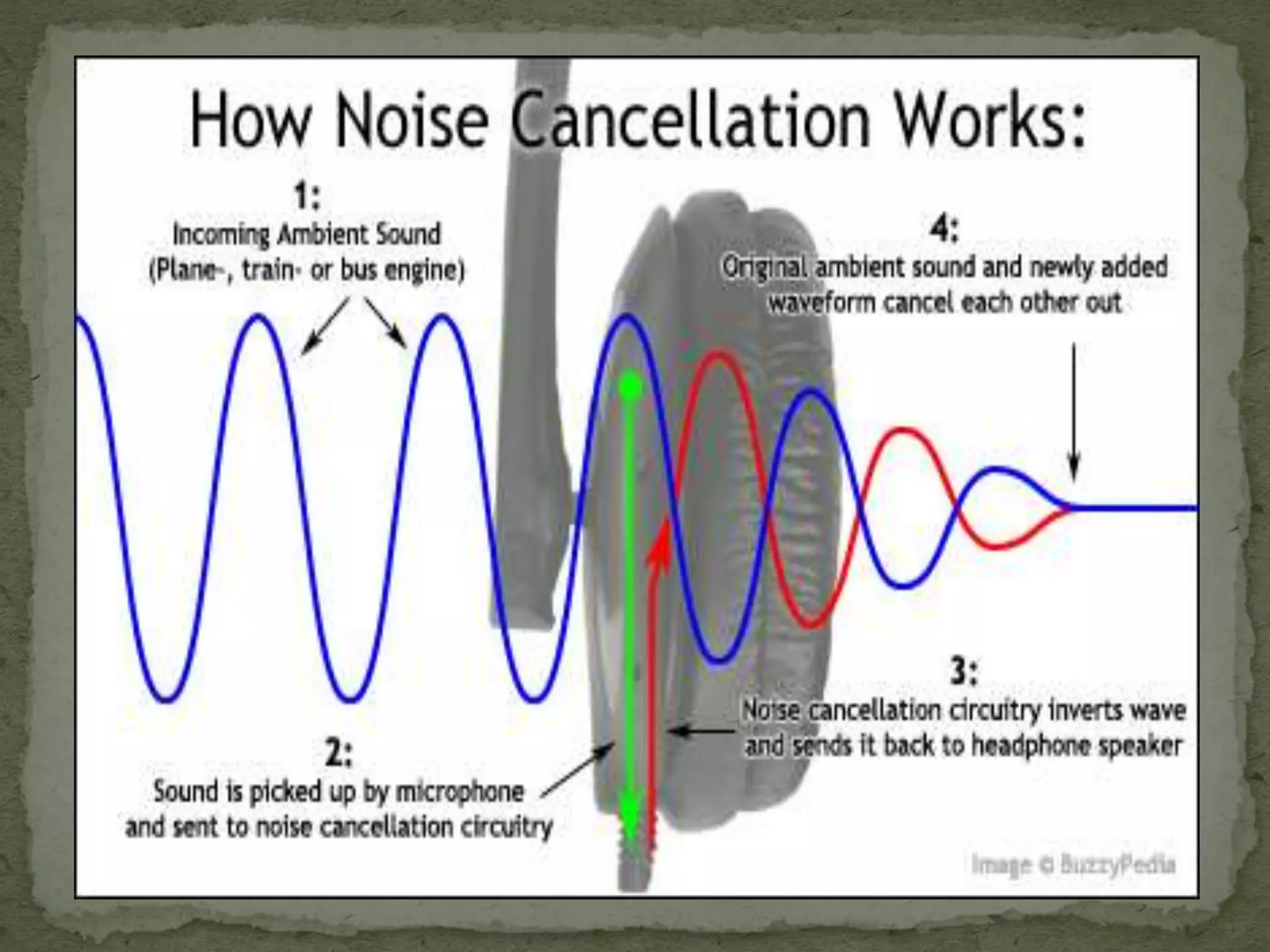
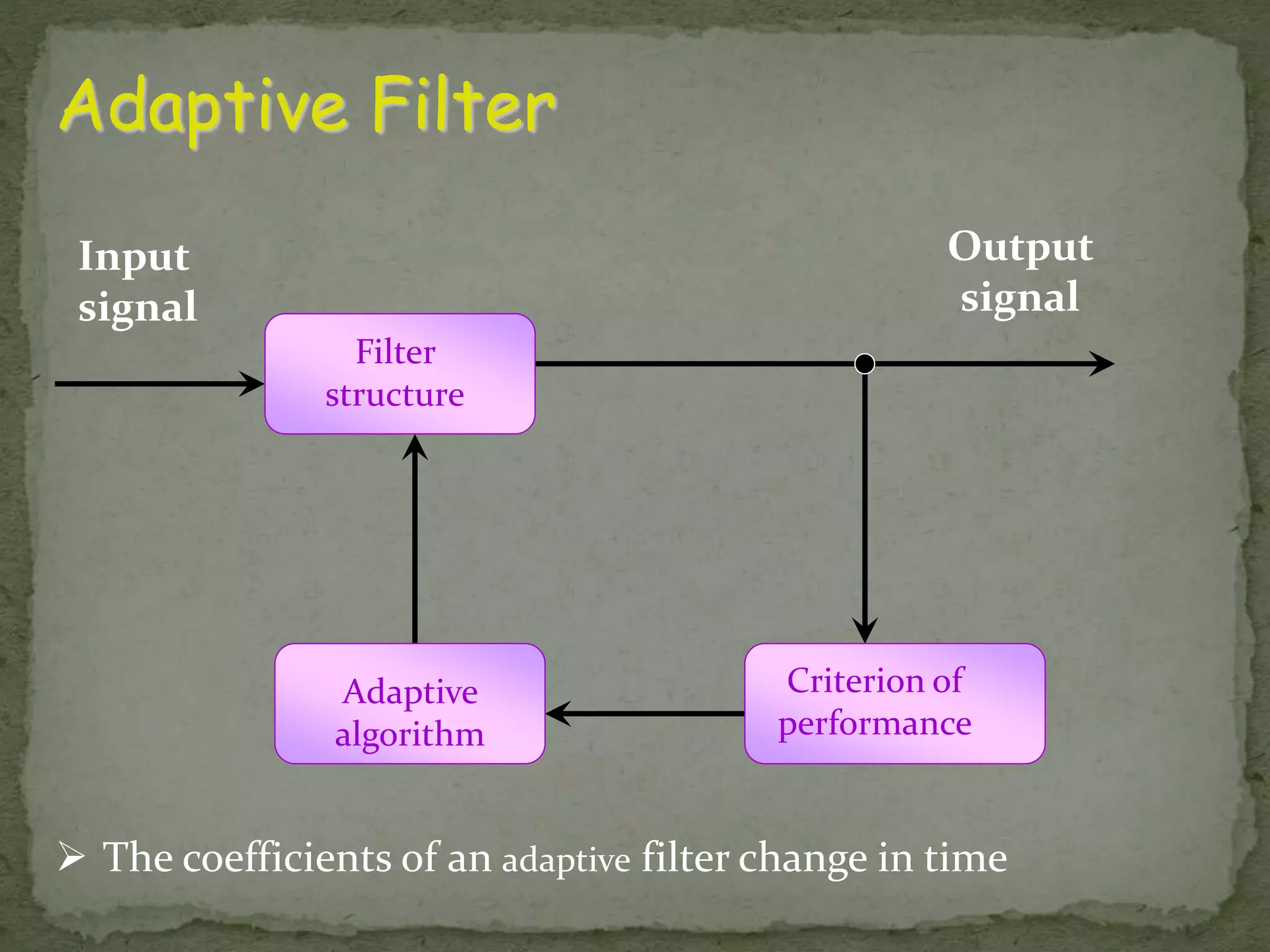
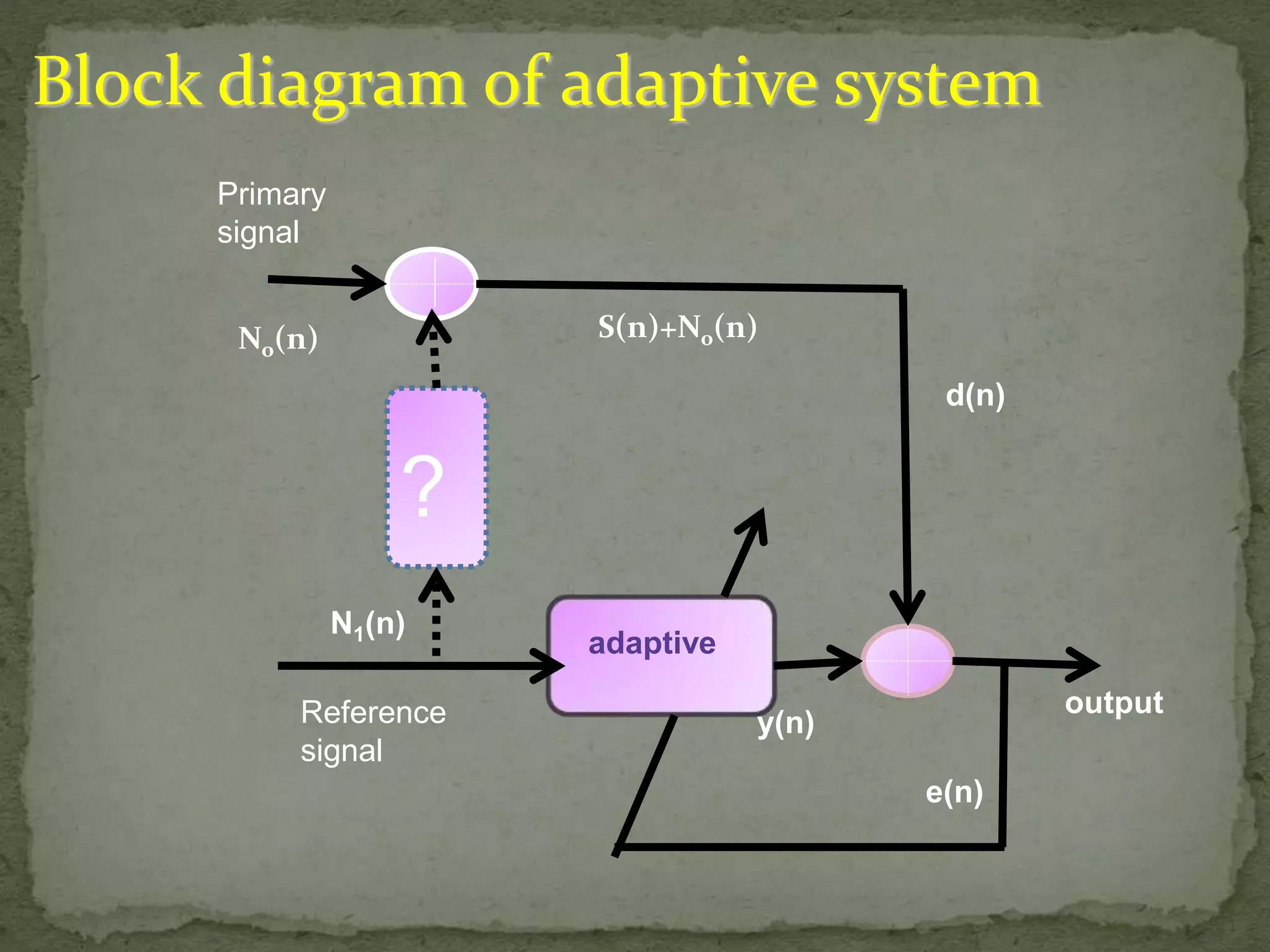
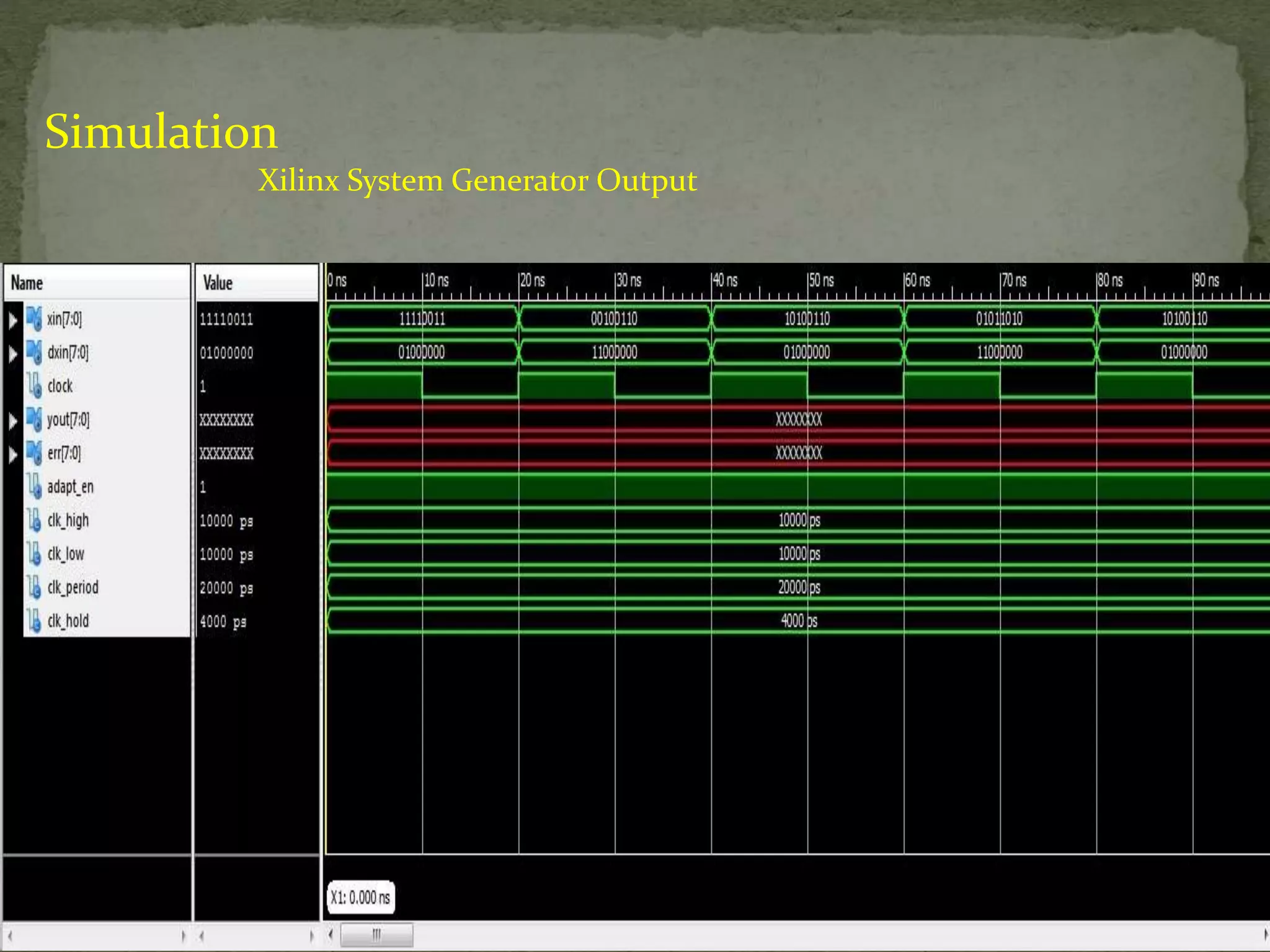
The document discusses the implementation and techniques involved in noise cancellation, focusing on the adaptive filter and the least mean square (LMS) algorithm. It explains the concept of noise, the principle behind noise cancellation, and the applications of these technologies in various fields. Additionally, it analyzes the advantages and operational aspects of the LMS algorithm, emphasizing its use in real-time adaptive filtering.