Introduction to Optimization.ppt

Introduction to Optimization.ppt

• 1.
  Introduction to Optimization Module1
• 2.
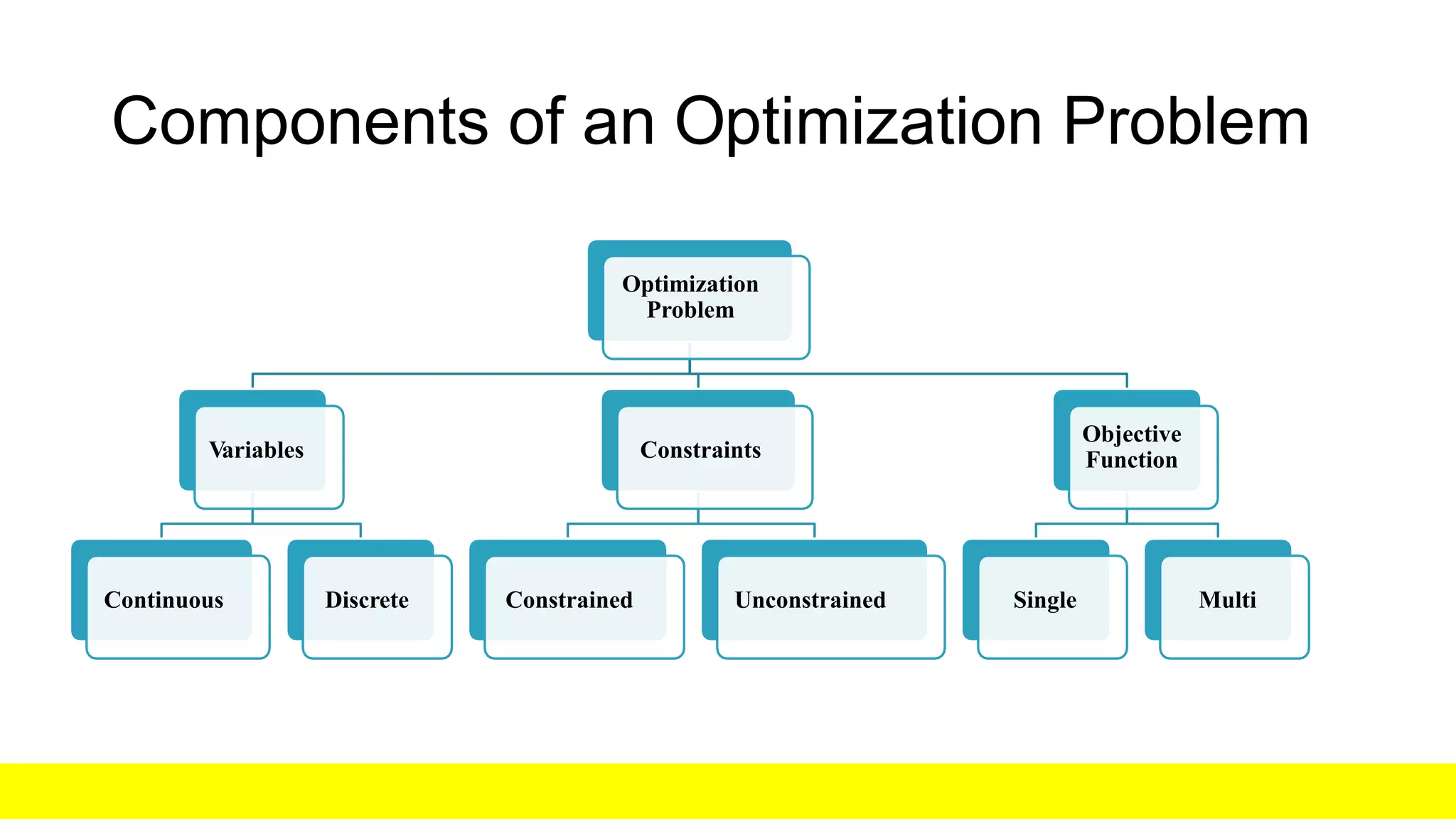
  What is Optimization? •The process of finding the best values for the variables of a particular problem to minimize or maximize an objective function • The action of making the best or most effective use of given situation - (Google dictionary) • It is a technique of squeezing best performance out of provided current state of model
• 3.
  Components of anOptimization Problem • Objective function An objective function express performance of a system, need to be minimized or maximized • Variable (Design or Decision Variable) A set of unknowns, define the objective function and constraints, can be continuous, discrete or boolean • Constraints They are conditions, allows the unknowns to take on certain values but exclude others to render the design to be feasible
• 4.
  Components of anOptimization Problem Optimization Problem Variables Continuous Discrete Constraints Constrained Unconstrained Objective Function Single Multi
• 5.
  Objective function 𝟏 𝟏𝟐 𝐟 𝐱 , 𝐱𝟐 = 𝐱𝟐+𝟐𝐱𝟐-0.3cos(3 𝛑𝐱𝟏)( 4 𝛑𝐱𝟐)+0.3 𝐨𝐛𝐣𝐞𝐜𝐭𝐢𝐯𝐞 𝐟𝐮𝐧𝐜𝐭𝐢𝐨𝐧 𝐦𝐢𝐧(𝐟) 𝐯𝐚𝐫𝐢𝐚𝐛𝐥𝐞𝐬 ∈ [𝟏𝟎, −𝟏𝟎] 𝐔𝐧𝐜𝐨𝐧𝐬𝐭𝐫𝐚𝐢𝐧𝐞𝐝 𝐏𝐫𝐨𝐛𝐥𝐞𝐦 𝐀𝐧 𝐞𝐱𝐚𝐦𝐩𝐥𝐞 ∶ 𝐬𝐢𝐧𝐠𝐥𝐞 𝐨𝐛𝐣𝐞𝐜𝐭𝐢𝐯𝐞 𝐟𝐮𝐧𝐜𝐭𝐢𝐨𝐧
• 6.
  Objective function 𝐀𝐧 𝐞𝐱𝐚𝐦𝐩𝐥𝐞∶ 𝐬𝐢𝐧𝐠𝐥𝐞 𝐨𝐛𝐣𝐞𝐜𝐭𝐢𝐯𝐞 𝐟𝐮𝐧𝐜𝐭 𝐢𝐨𝐧 Min f(z1, z2, z3) = (-100-(z1-5)2 - (z2-5)2 +(z3-5)2)/100 Subject to; h(z1, z2, z3) = (z1 - 3)2 + (z2 - 2)2 + (z3 - 5)2 – 0.0625 ≤ 0 where; 0 ≤ zi ≤ 10; 𝐂𝐨𝐧𝐬𝐭𝐫𝐚𝐢𝐧𝐞𝐝 𝐏𝐫𝐨𝐛𝐥𝐞𝐦
• 7.
  Objective function 𝐀𝐧 𝐞𝐱𝐚𝐦𝐩𝐥𝐞∶ 𝐌𝐮𝐥𝐭𝐢 𝐨𝐛𝐣𝐞𝐜𝐭𝐢𝐯𝐞 𝐟𝐮𝐧𝐜𝐭𝐢𝐨𝐧 𝐨𝐛𝐣𝐞𝐜𝐭𝐢𝐯𝐞 𝐟𝐮𝐧𝐜𝐭𝐢𝐨𝐧 𝐦𝐢𝐧(𝐟𝟏 ) & 𝐦𝐢𝐧(𝐟𝟐 ) & 𝐦𝐢𝐧(𝐟𝟑 ) 𝐔𝐧𝐜𝐨𝐧𝐬𝐭𝐫𝐚𝐢𝐧𝐞𝐝 𝐏𝐫𝐨𝐛𝐥𝐞𝐦
• 8.
  𝐀𝐧 𝐞𝐱𝐚𝐦𝐩𝐥𝐞 ∶𝐌𝐮𝐥𝐭𝐢 𝐨𝐛𝐣𝐞𝐜𝐭𝐢𝐯𝐞 𝐟𝐮𝐧𝐜𝐭𝐢𝐨𝐧 𝒎𝒊𝒏 = 𝐬𝐮𝐛𝐣𝐞𝐜𝐭 𝐭𝐨; 𝐂𝐨𝐧𝐬𝐭𝐫𝐚𝐢𝐧𝐞𝐝 𝐏𝐫𝐨𝐛𝐥𝐞𝐦 Objective function {
• 9.
  Type of OptimizationTechniques Optimization Technique Conventional Mathematical Programming Calculus Methods Network Methods Nonconventional Meta-heuristic algorithms
• 10.
  Meta-heuristicAlgorithms • Meta-heuristic isa general algorithmic framework which can be applied to different optimization problems with relatively few modifications to make them adapted to a specific problem.
• 11.
  Meta-heuristicAlgorithms Meta-heuristic algorithms Evolutionary algorithms GA GP Physics-based algorithms CSS SA Swarm-based algorithms WhaleAnt Colony Human-based algorithms TLBO EMA Genetic Algorithm (GA) Genetic Programming (GP) Charged System Search (CSS) Simulated Annealing(SA) Teaching Learning Based Optimization(TLBO) Exchange Market Algorithm (EMA)
• 12.
  An Example :Whale optimization algorithm 1 Encircling prey 2 Bubble-net attacking method (exploitation phase) 3 Search for prey (exploration phase) Behavior of Whale
• 13.
  An Example :Whale optimization algorithm Mathematical Model 1- Encircling prey Where t is the current iteration, A and C are coefficient vectors, X* is the position vector of the best solution, and X indicates the position vector of a solution, | | is the absolute value.
• 14.
  An Example :Whale optimization algorithm Where components of a are linearly decreased from 2 to 0 over the course of iterations and r is random vector in [0; 1] Mathematical Model (cont.) The vectors A and C are calculated asfollows:
• 15.
  An Example :Whale optimization algorithm Mathematical Model (cont.) 2- Bubble-net mechanism (exploitationphase) Where the value of A is a random value in interval [-a, a] and the value of a is decreased from 2 to 0 , D’ =| X*(t) - X(t) | is the distance between the prey (best solution) and the ith whale, b is a constant, l is a random number in [-1; 1], and p is a random number in [0; 1]
• 16.
  An Example :Whale optimization algorithm Mathematical Model (cont.) 3- search for prey (exploration phase) In order to force the search agent to move far a way from reference whale, we use the A with values > 1 or < 1 Where Xrand is a random position vector chosen from the current population.
• 17.
  Module 1: Introductionto Optimization • END OF CONTENT MODULE