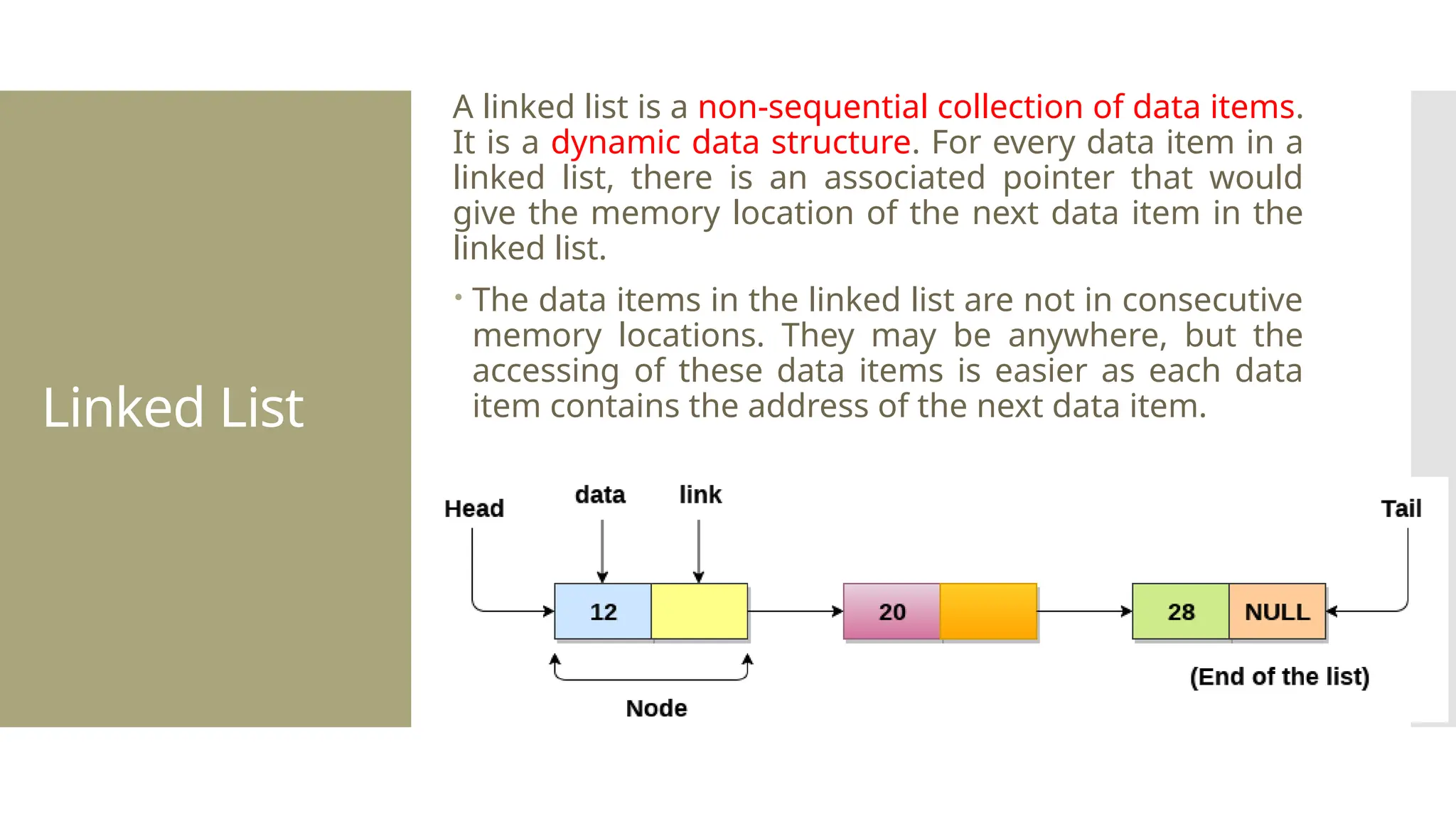
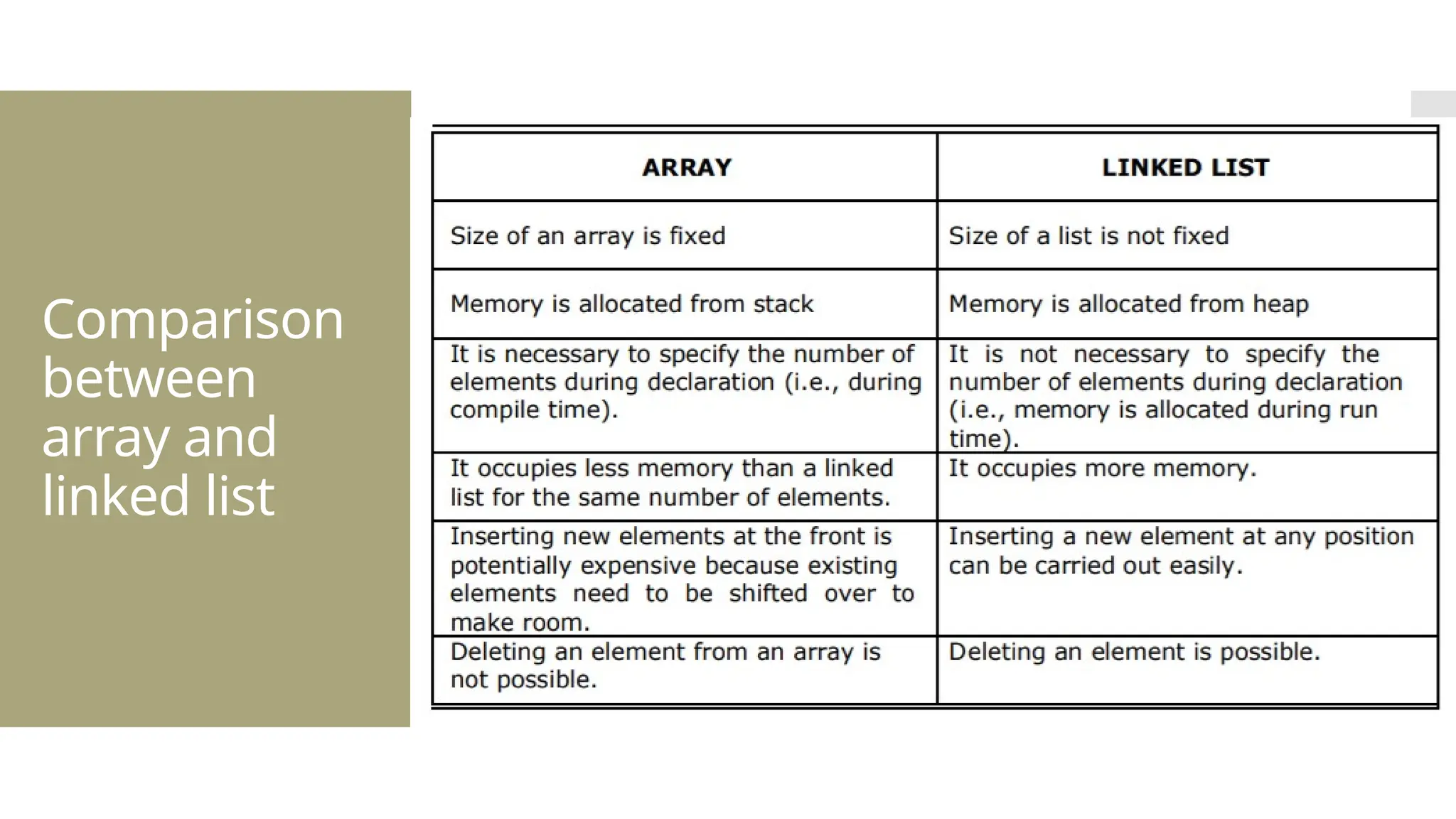
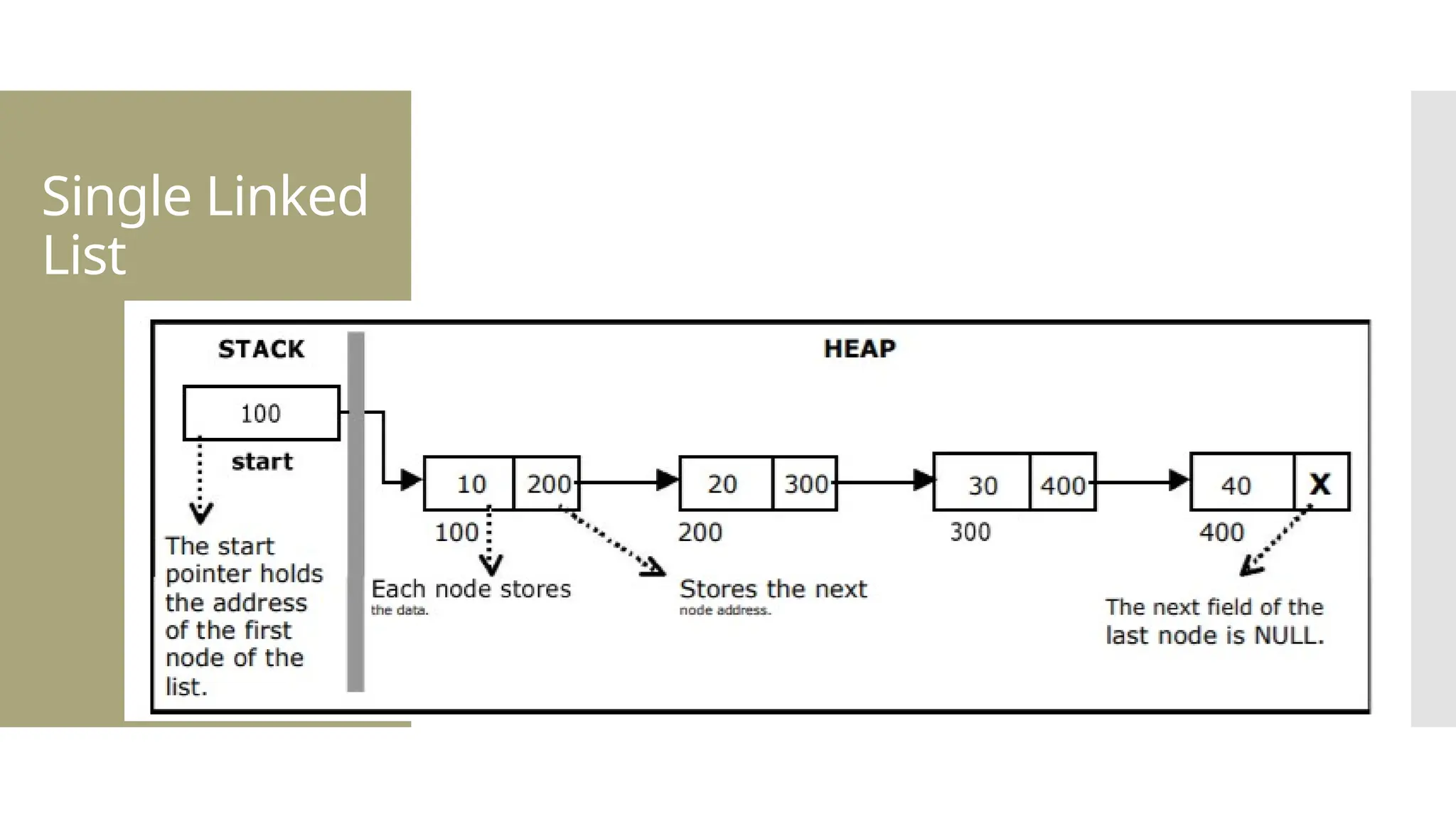
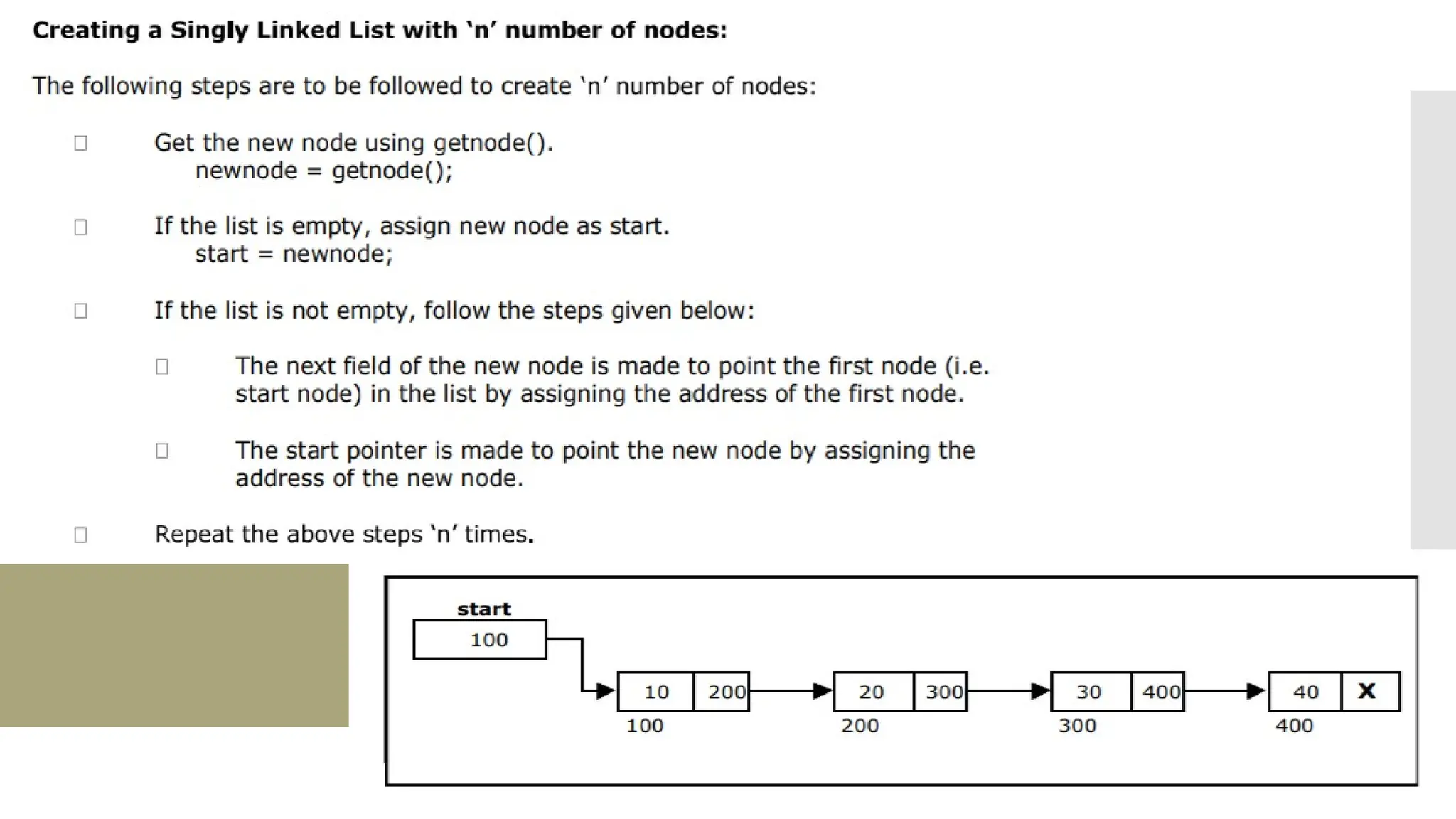
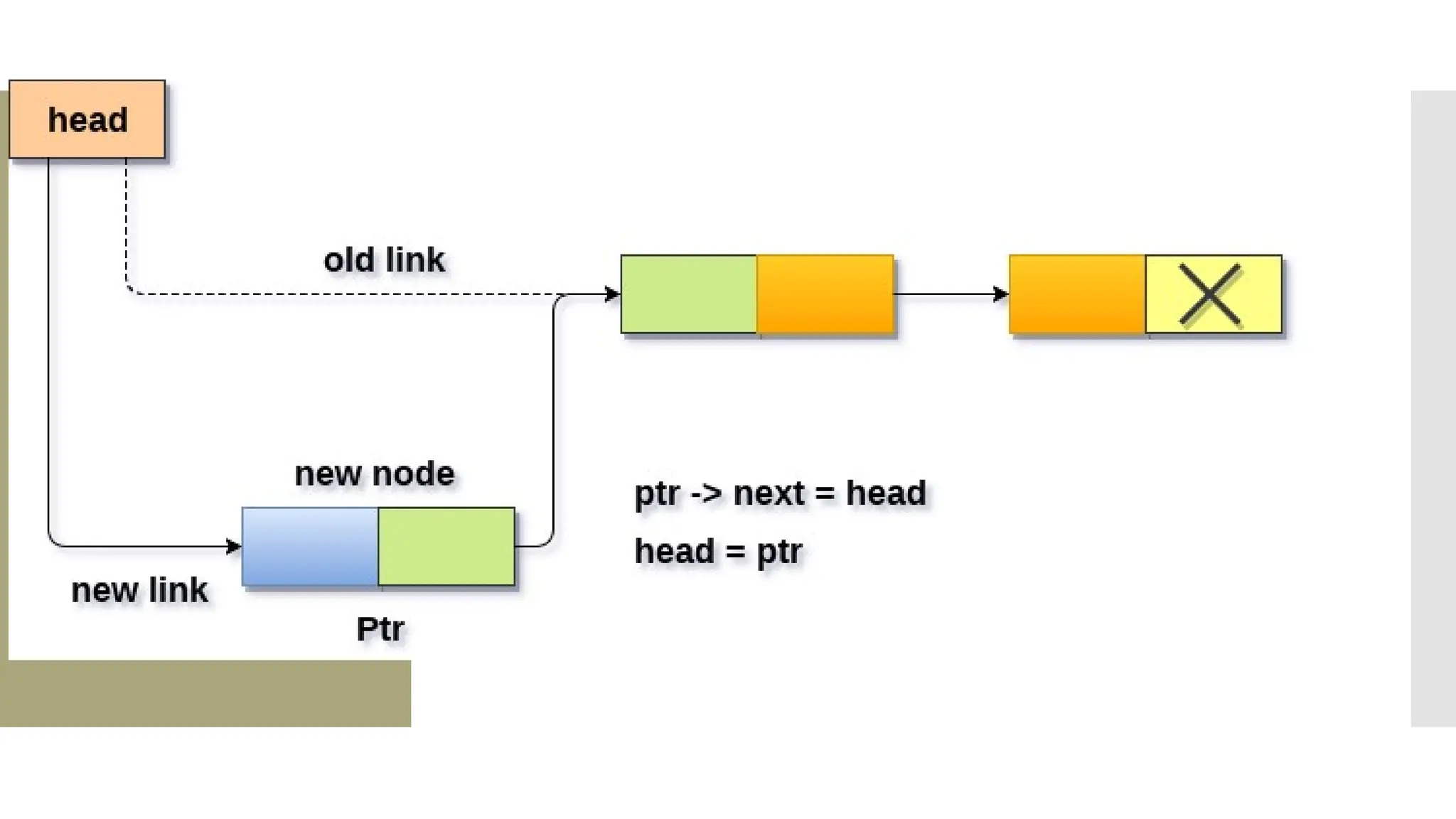
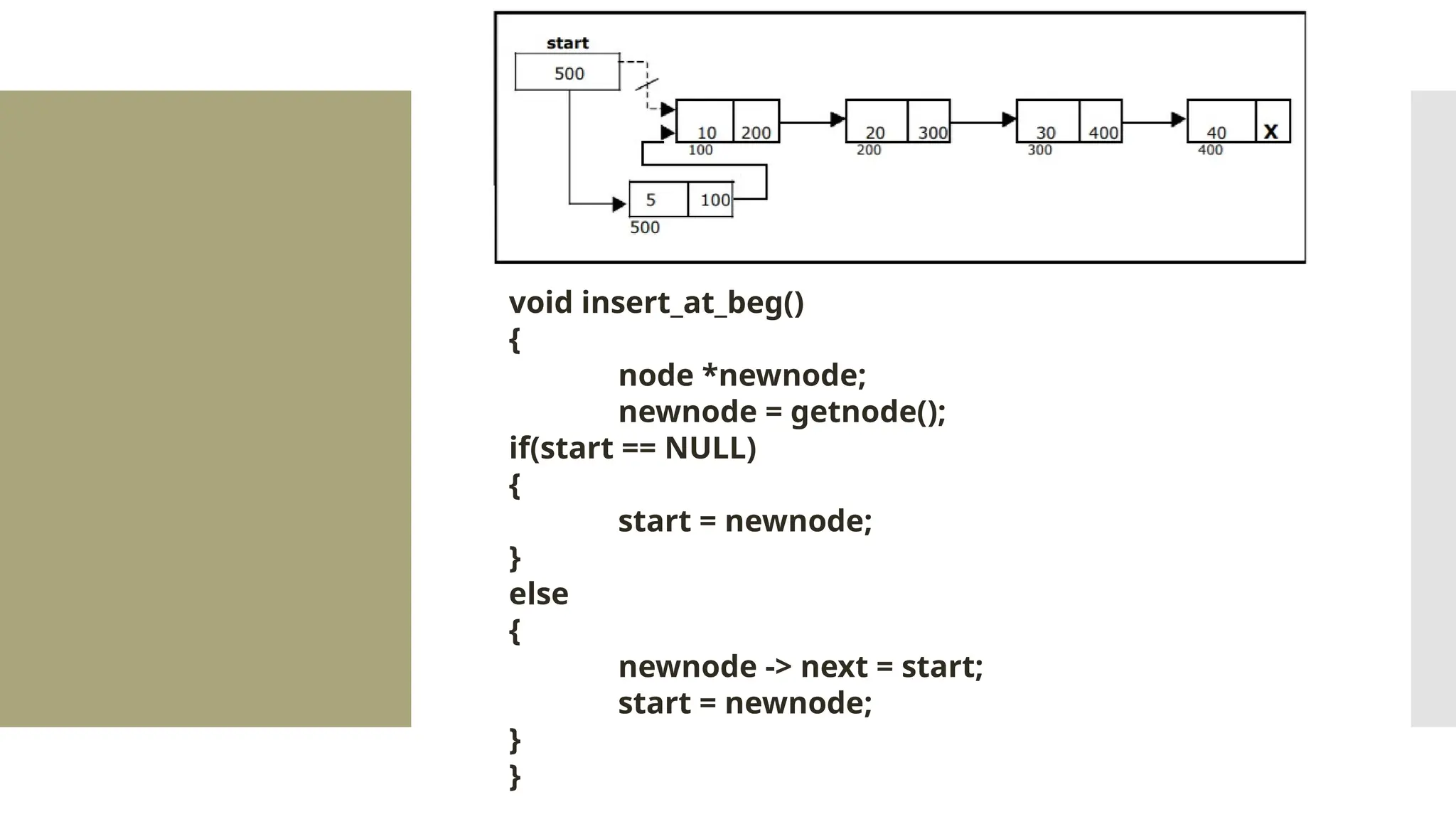
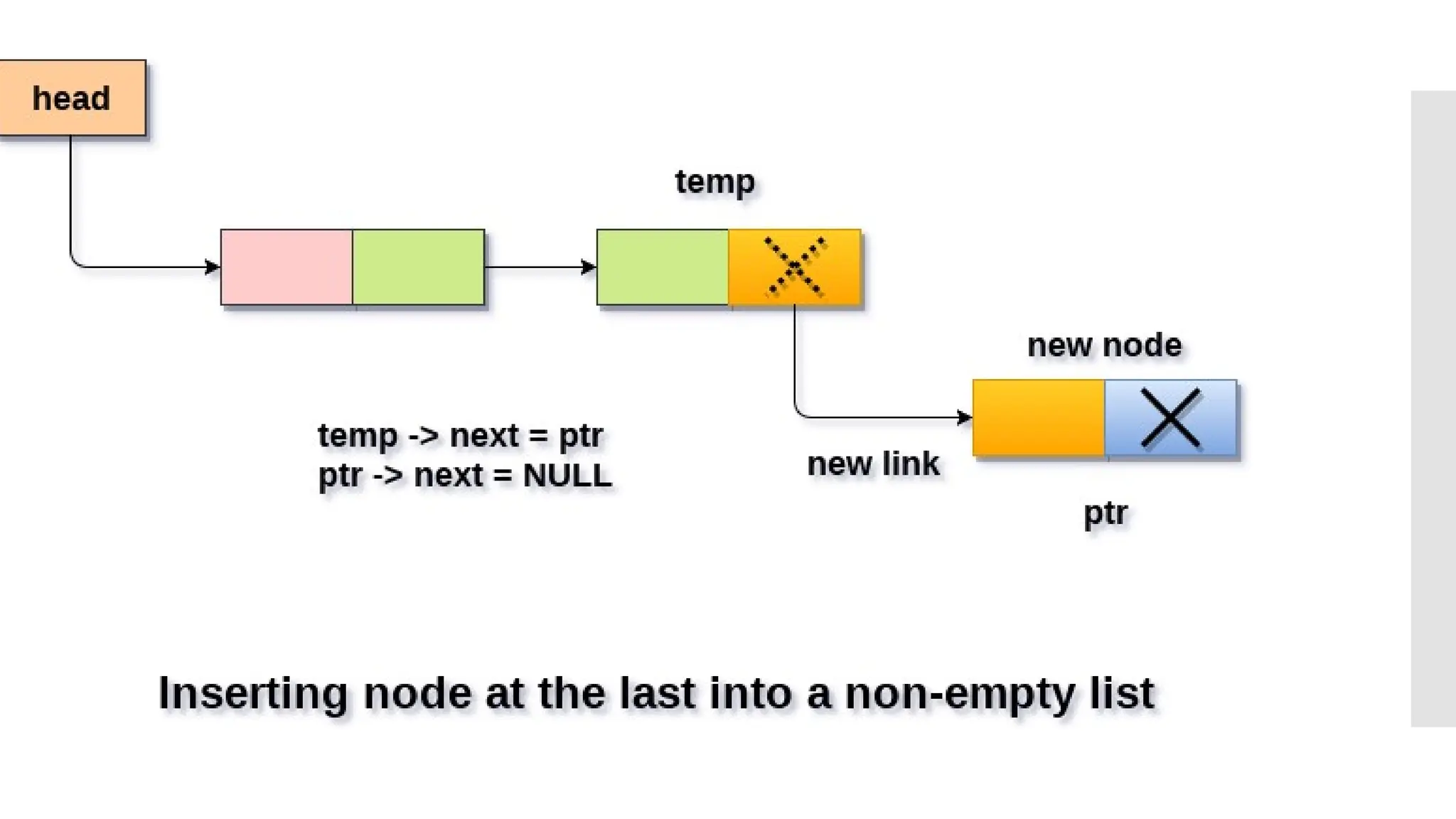
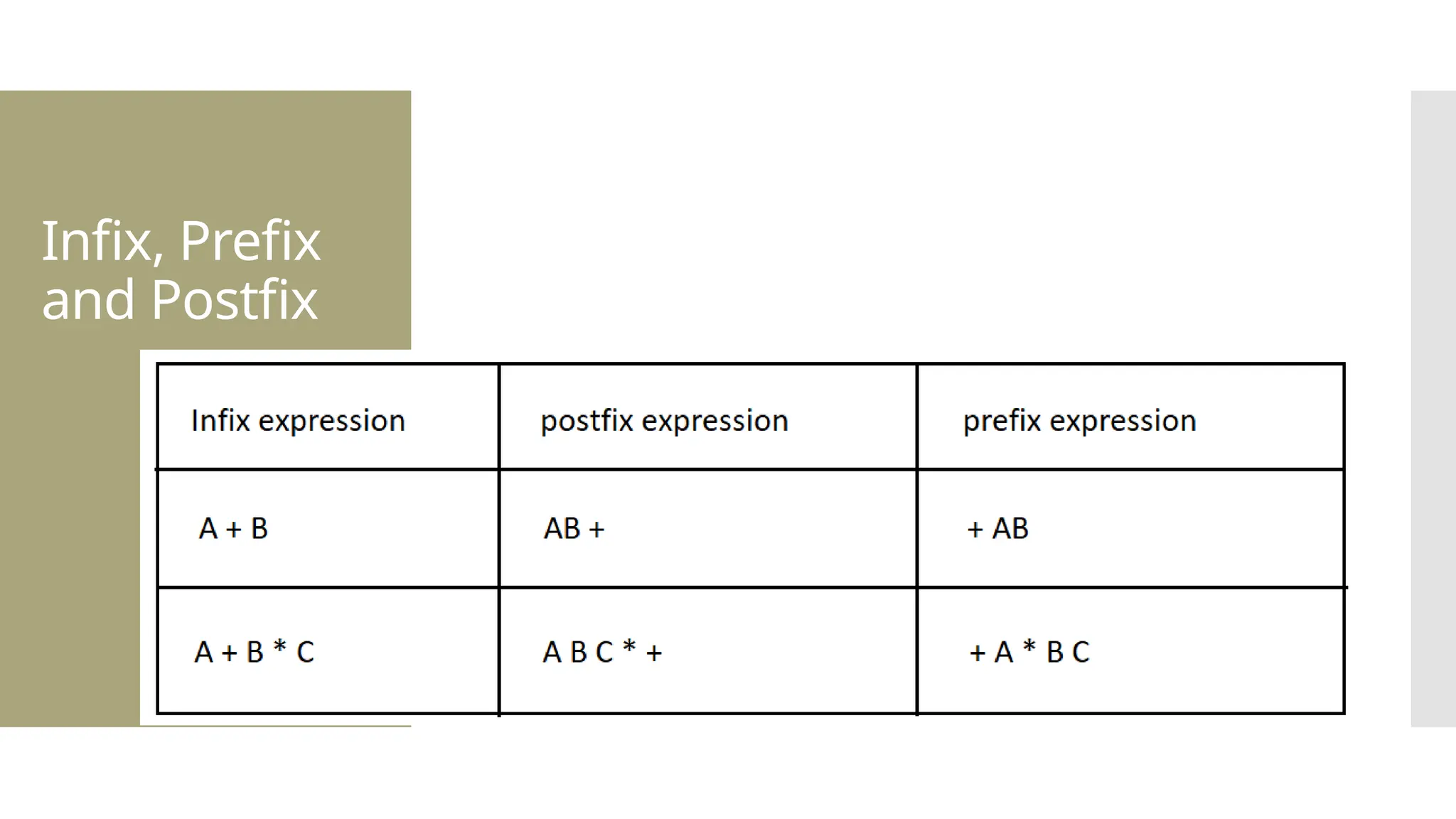
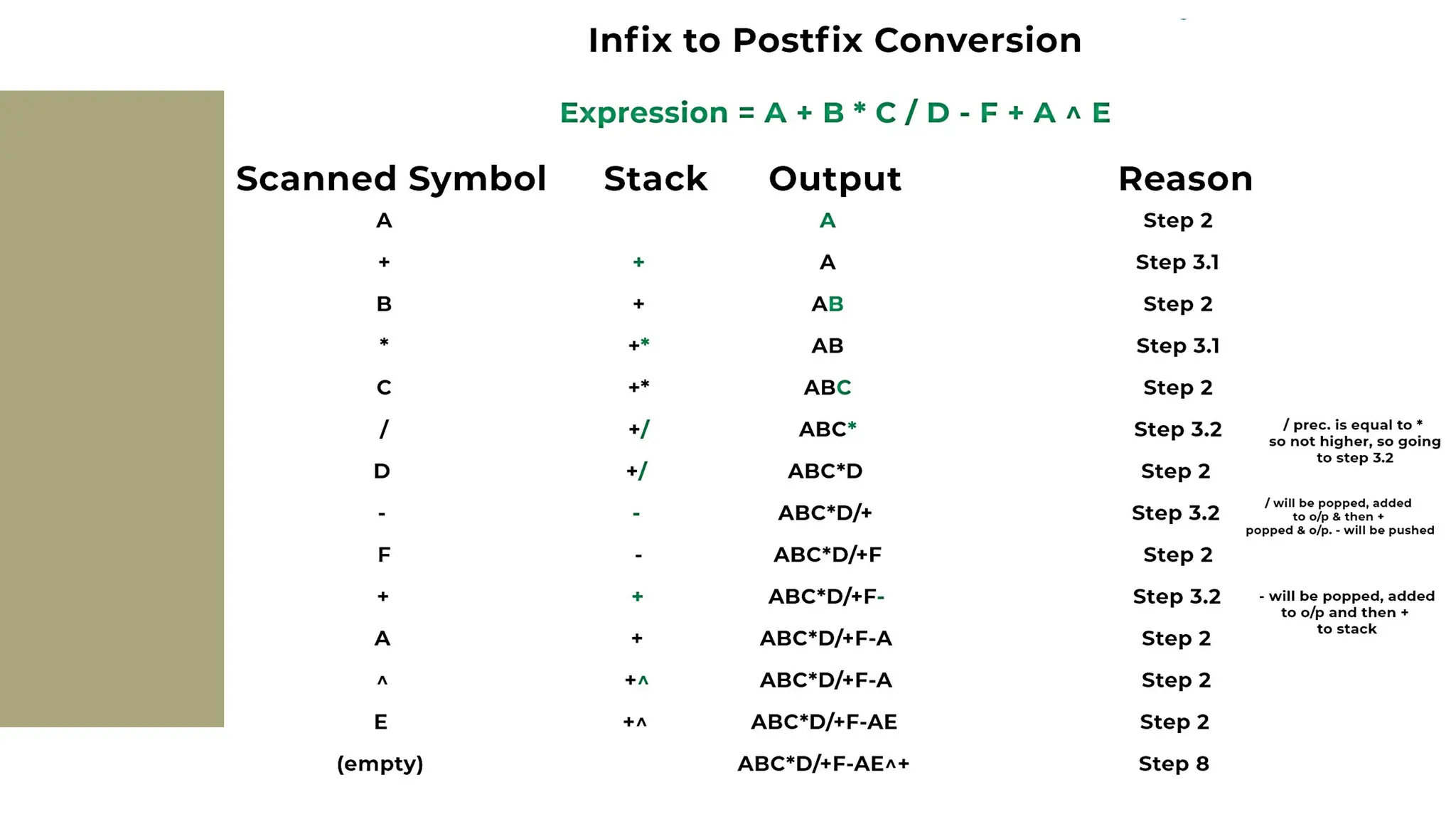
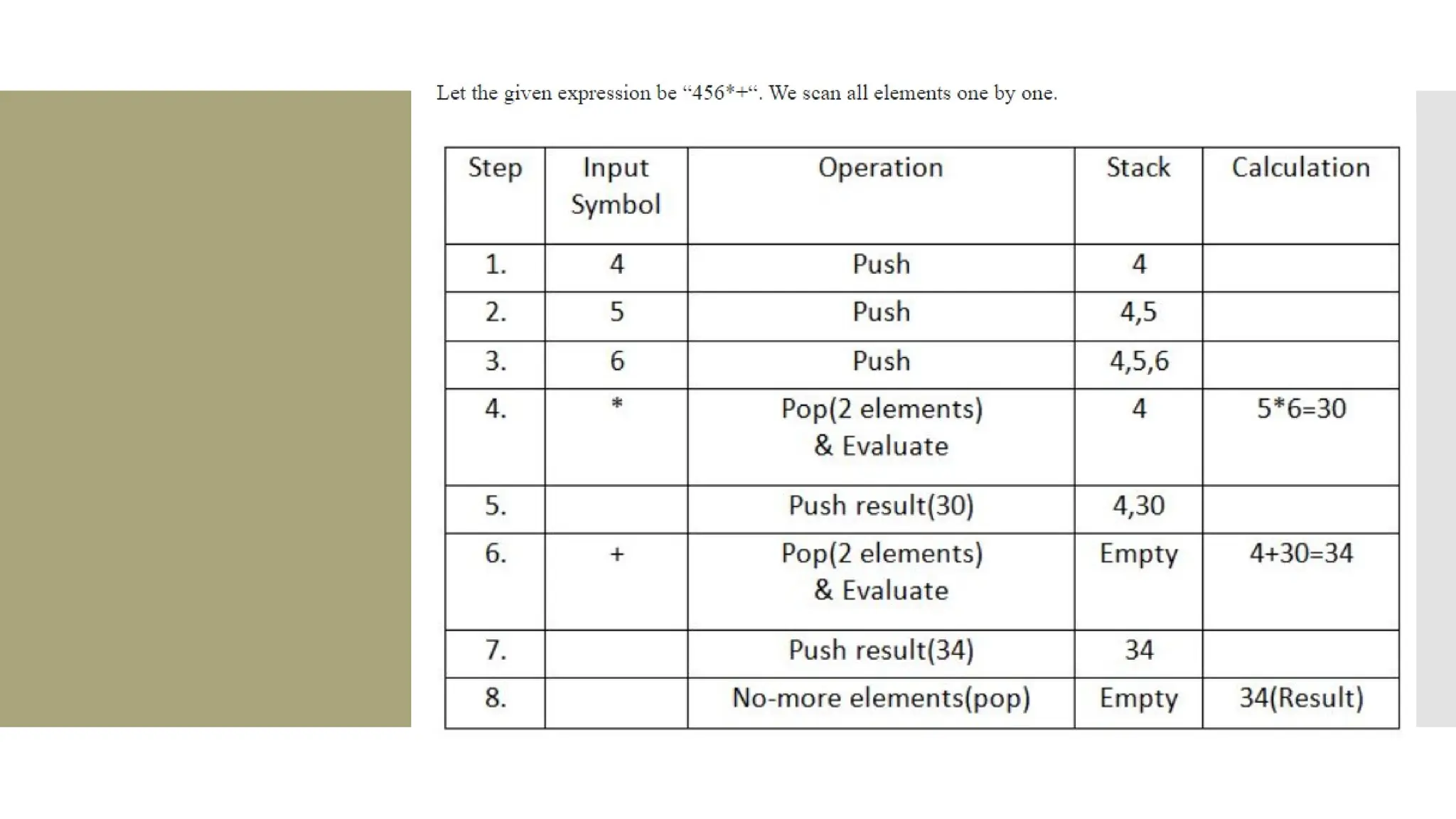
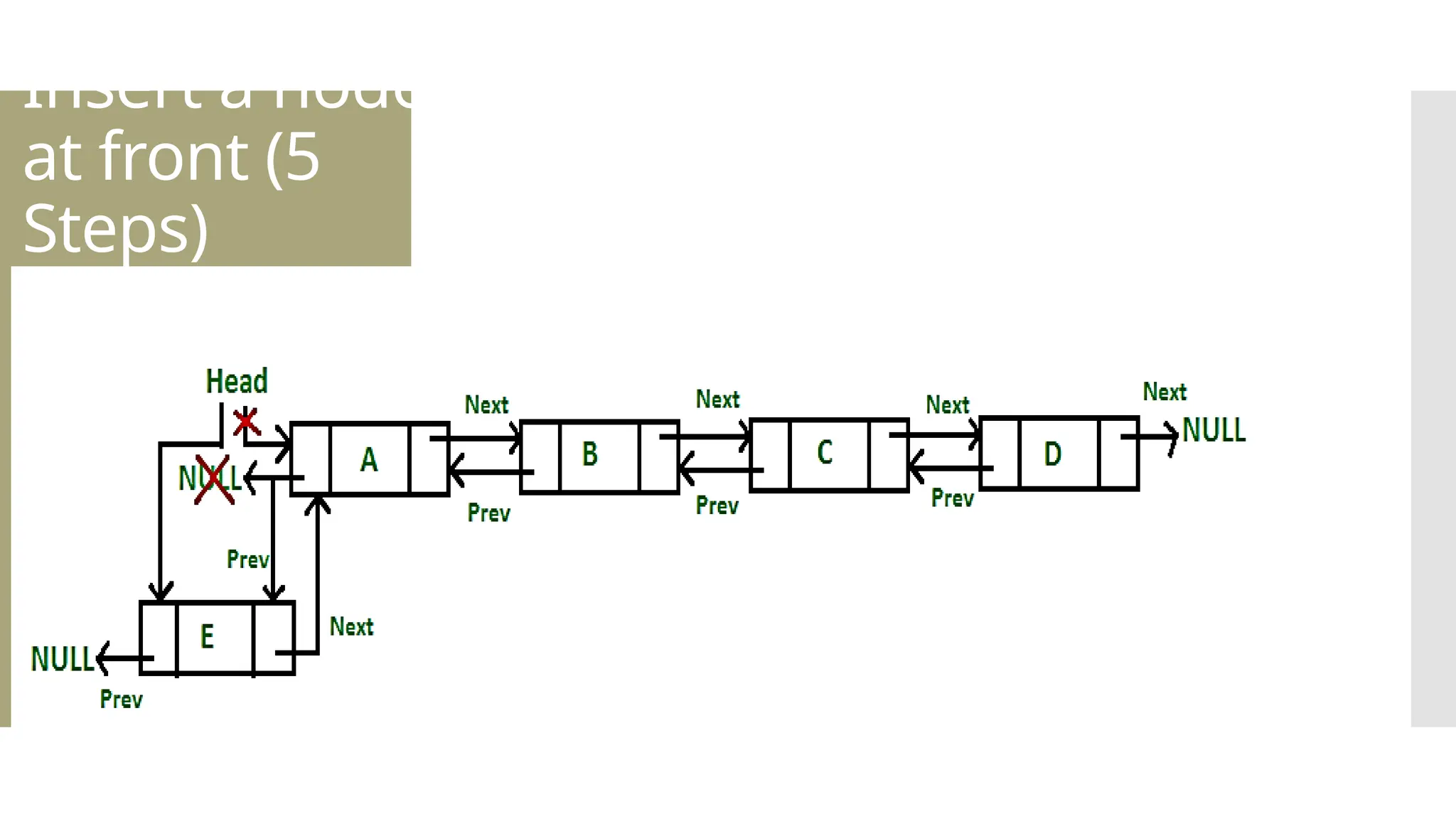
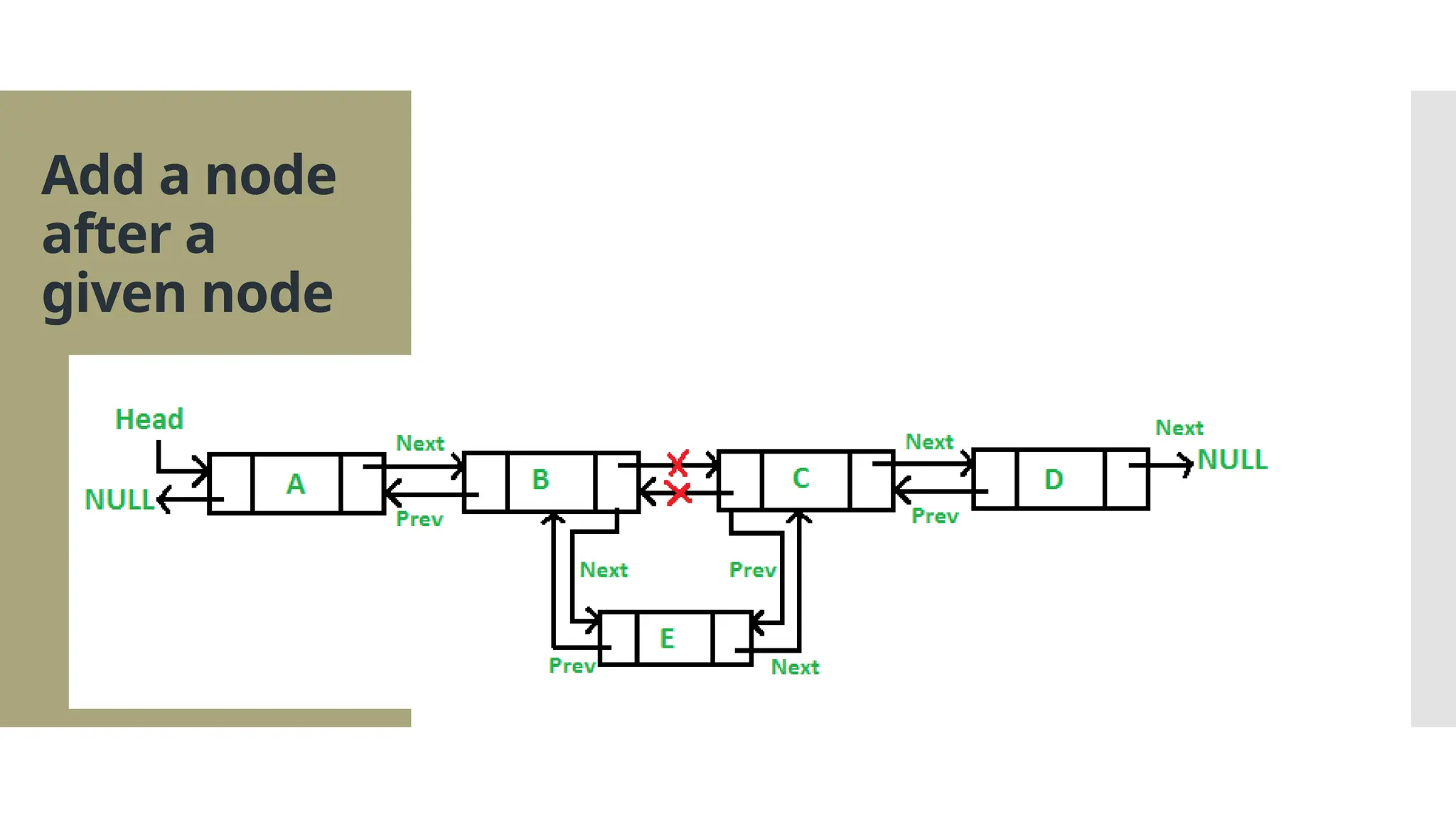
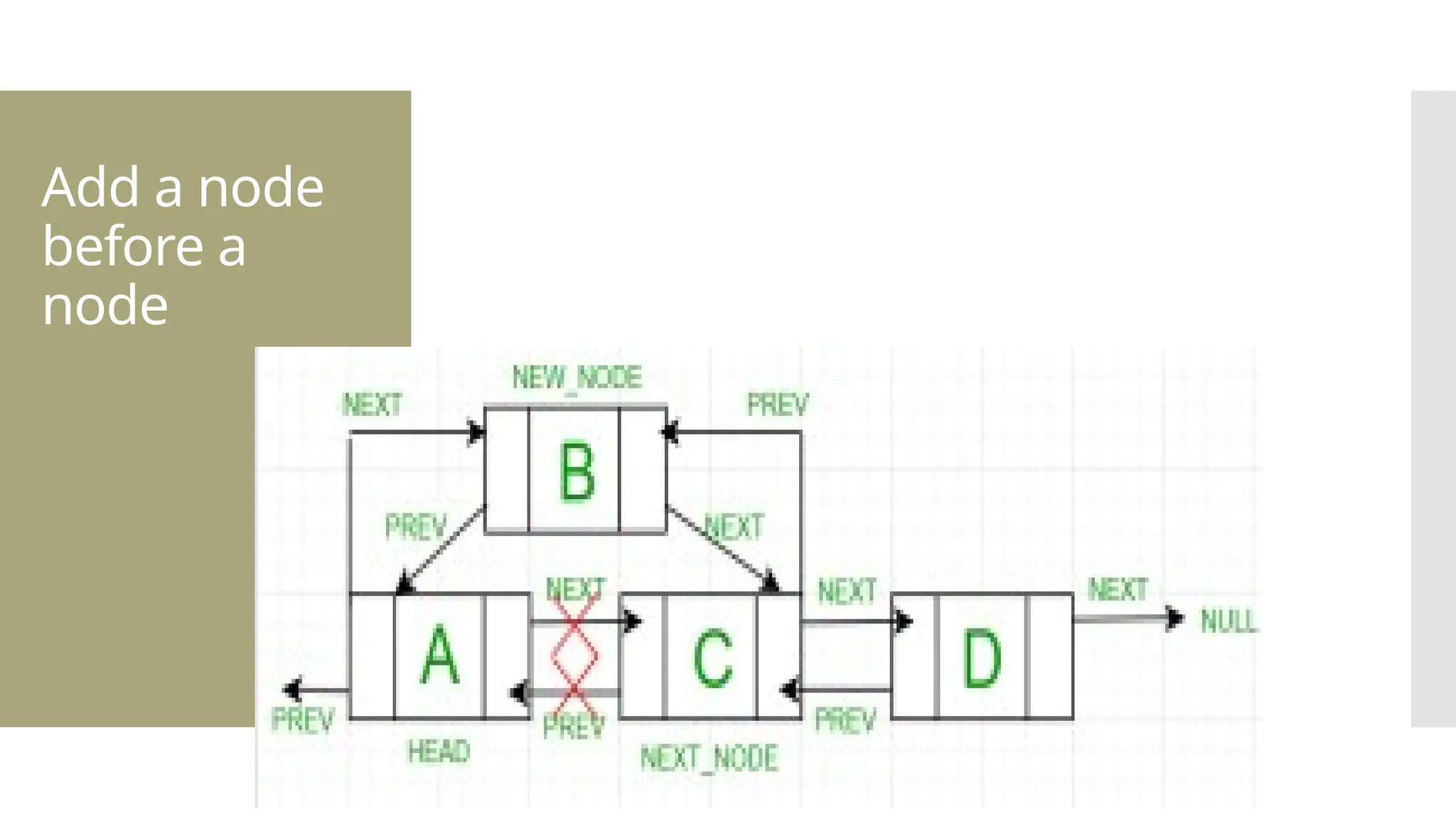
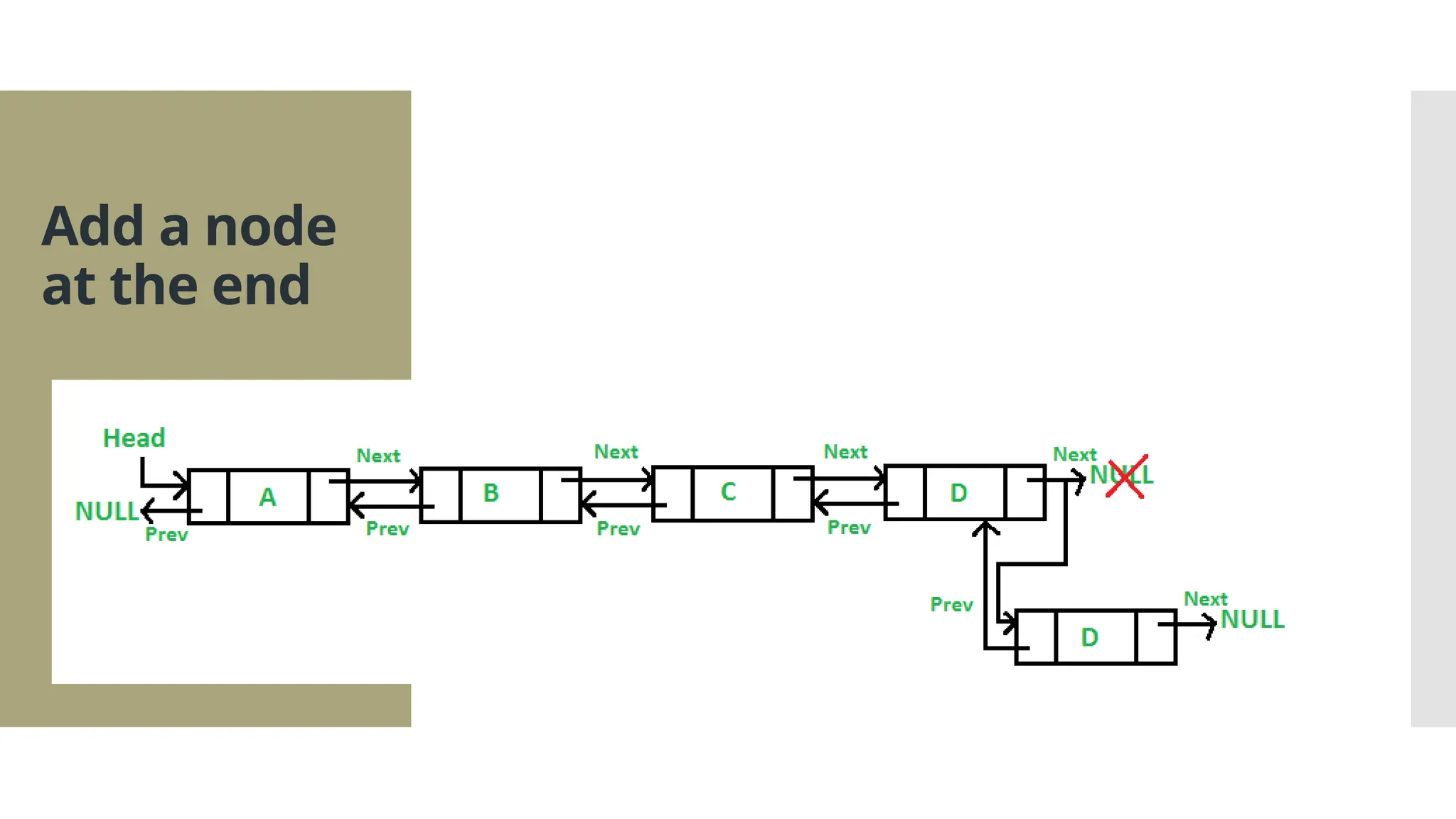
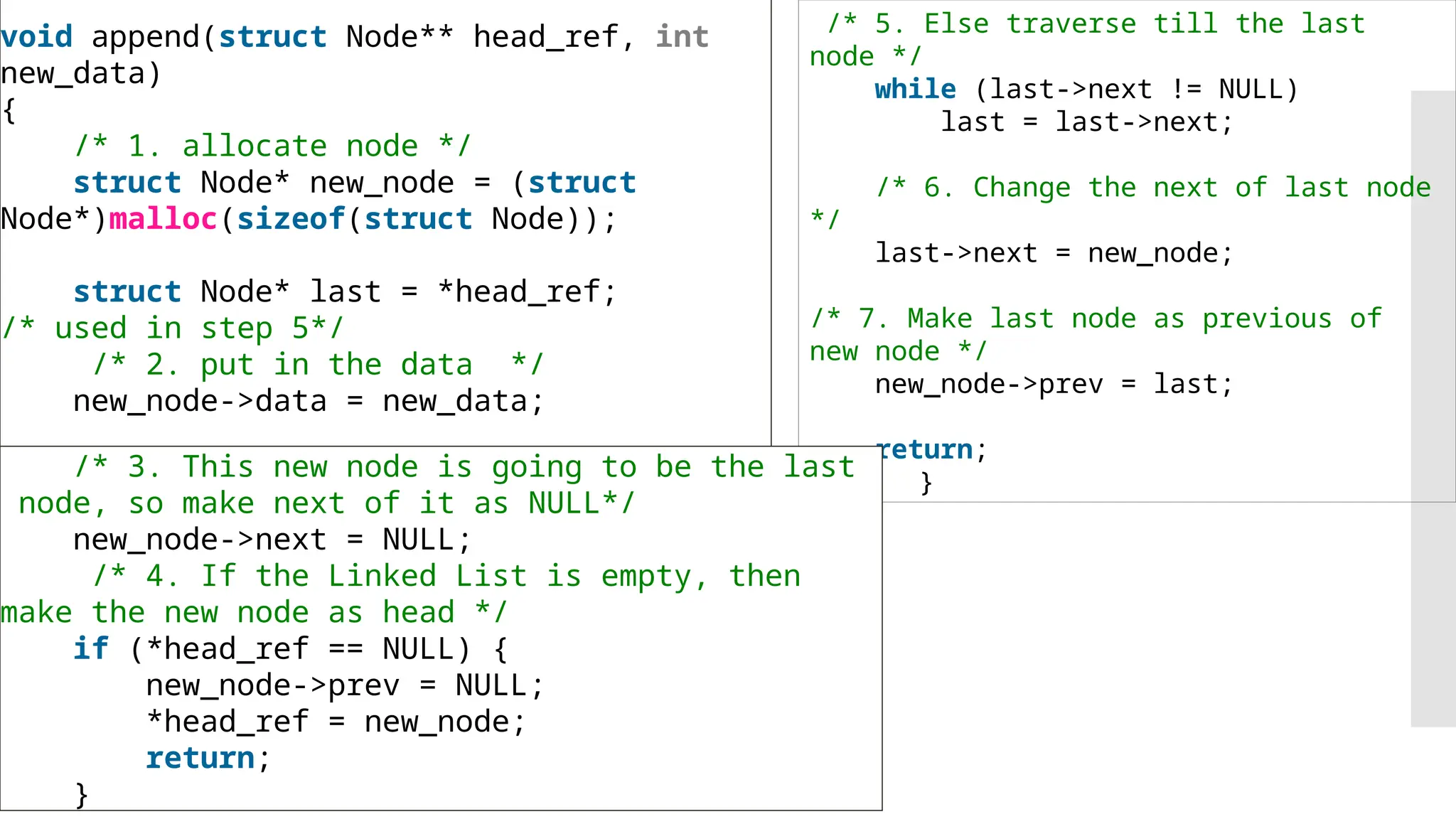
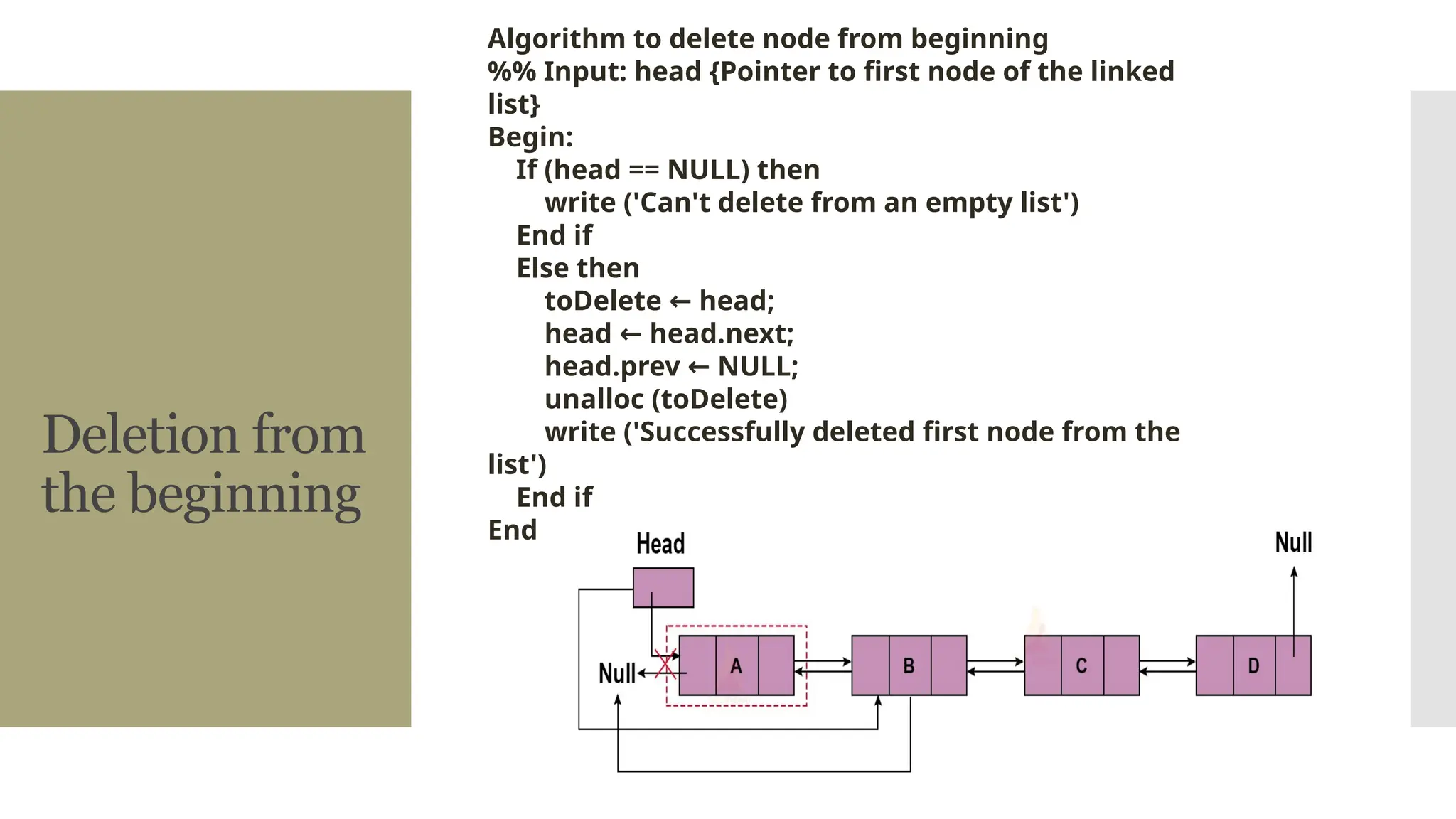
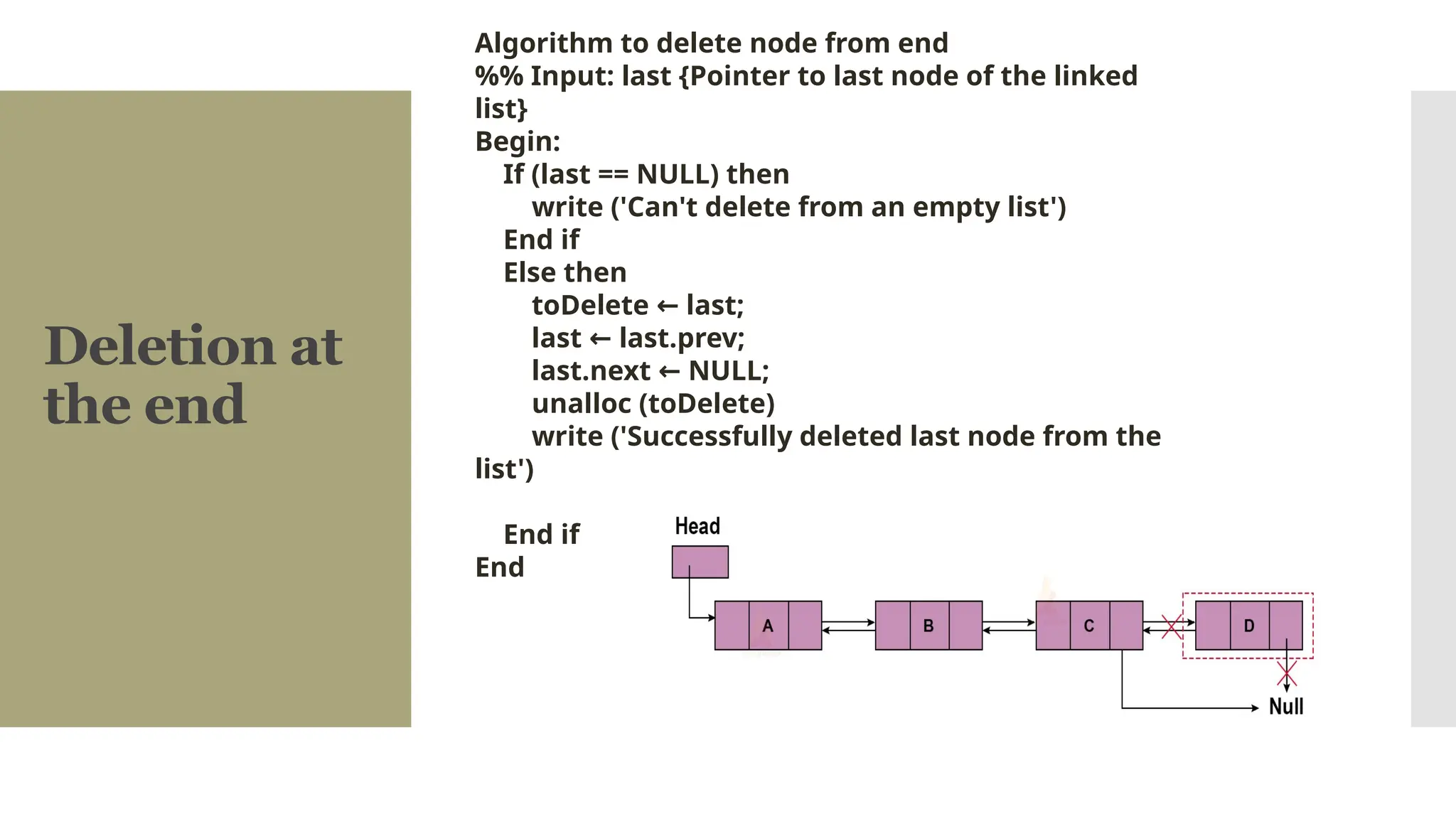
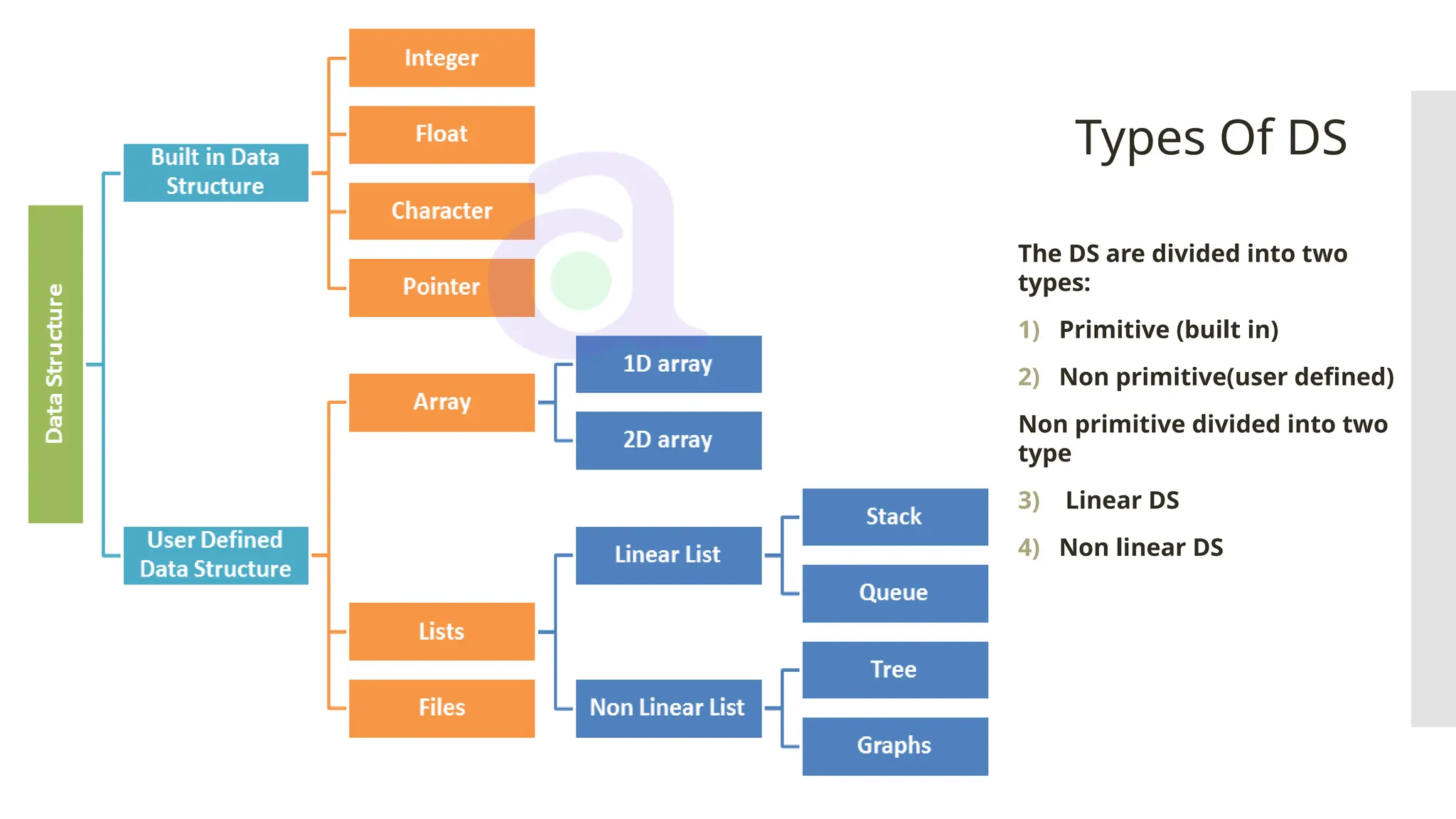
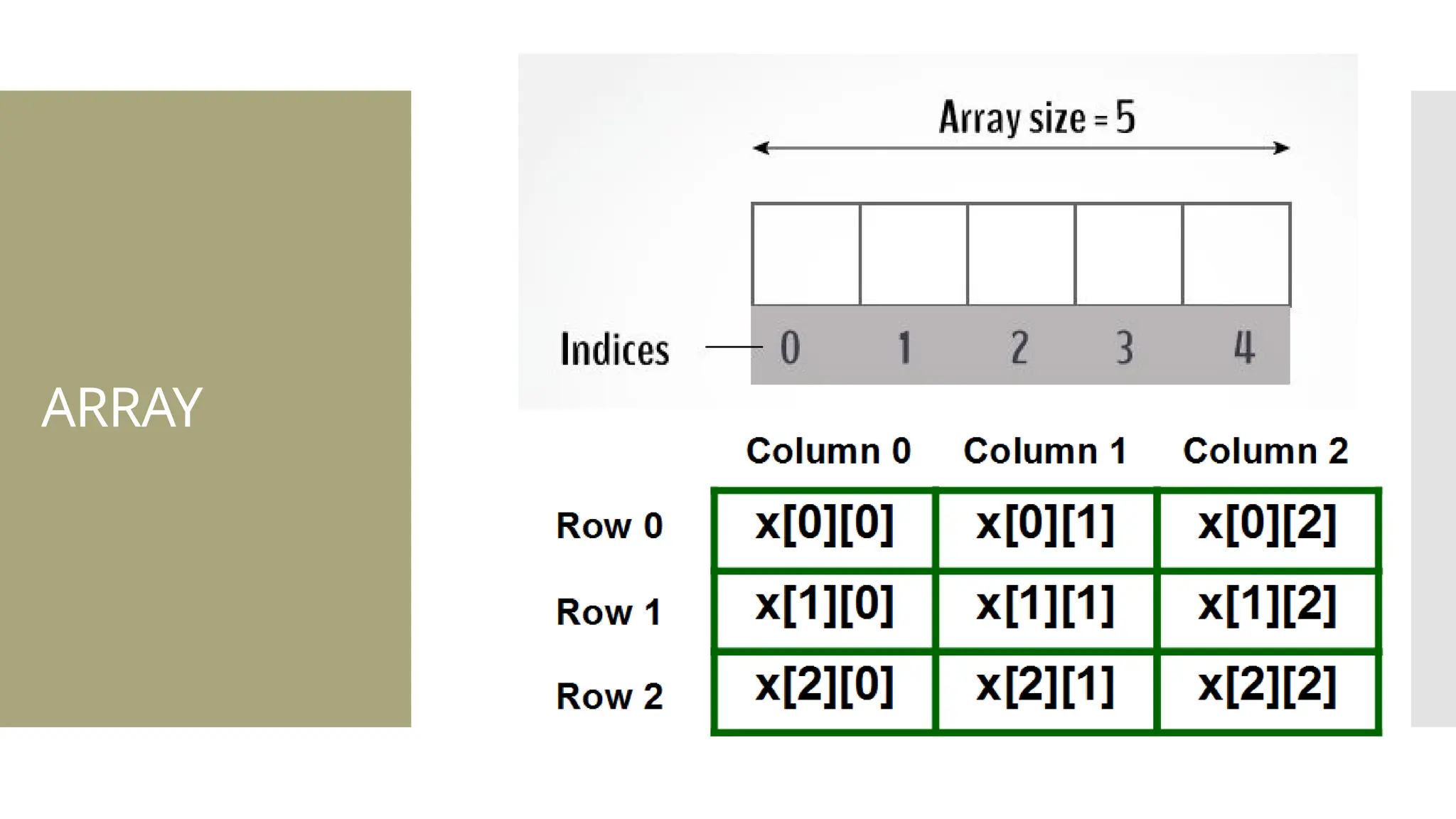
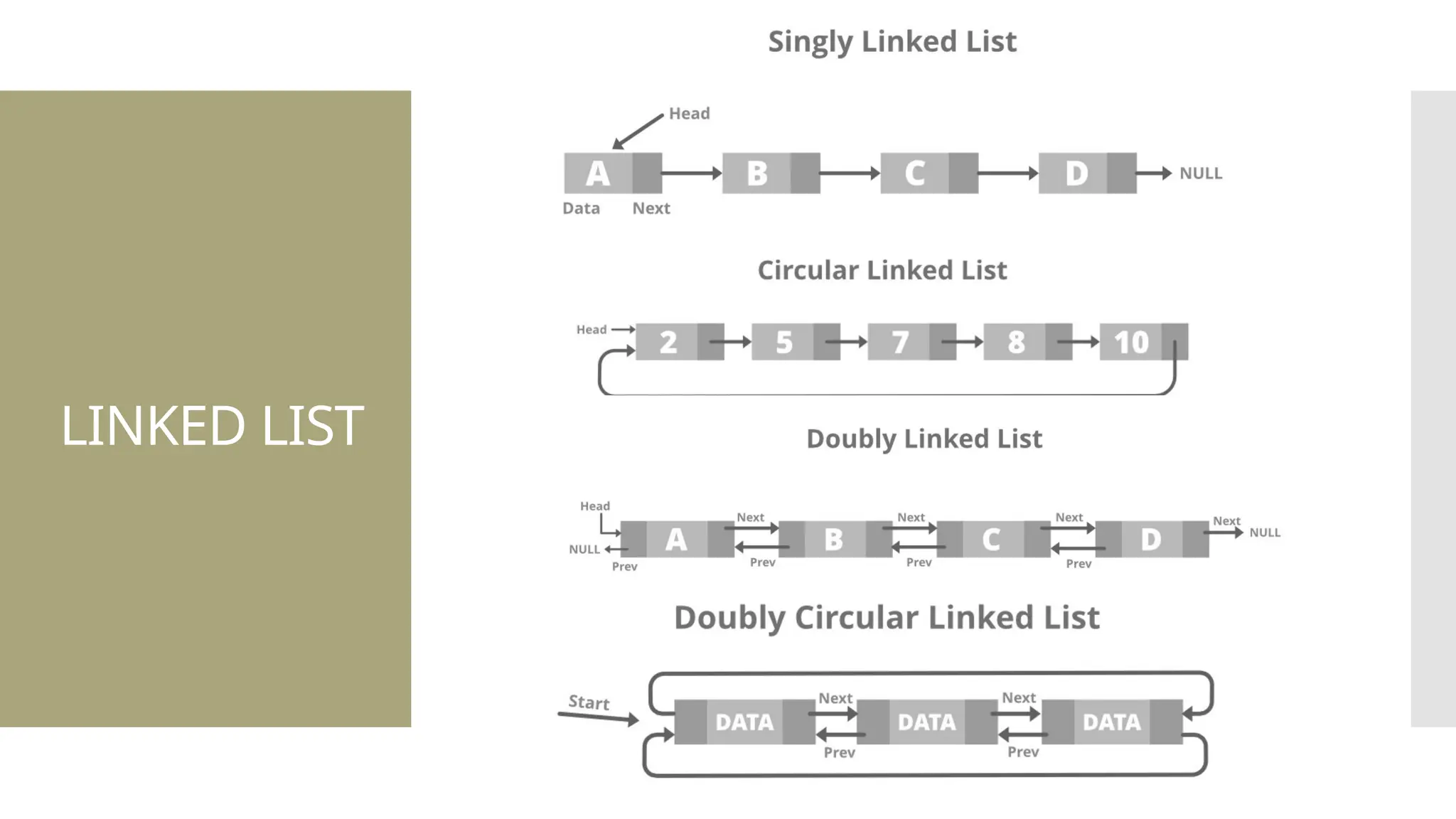
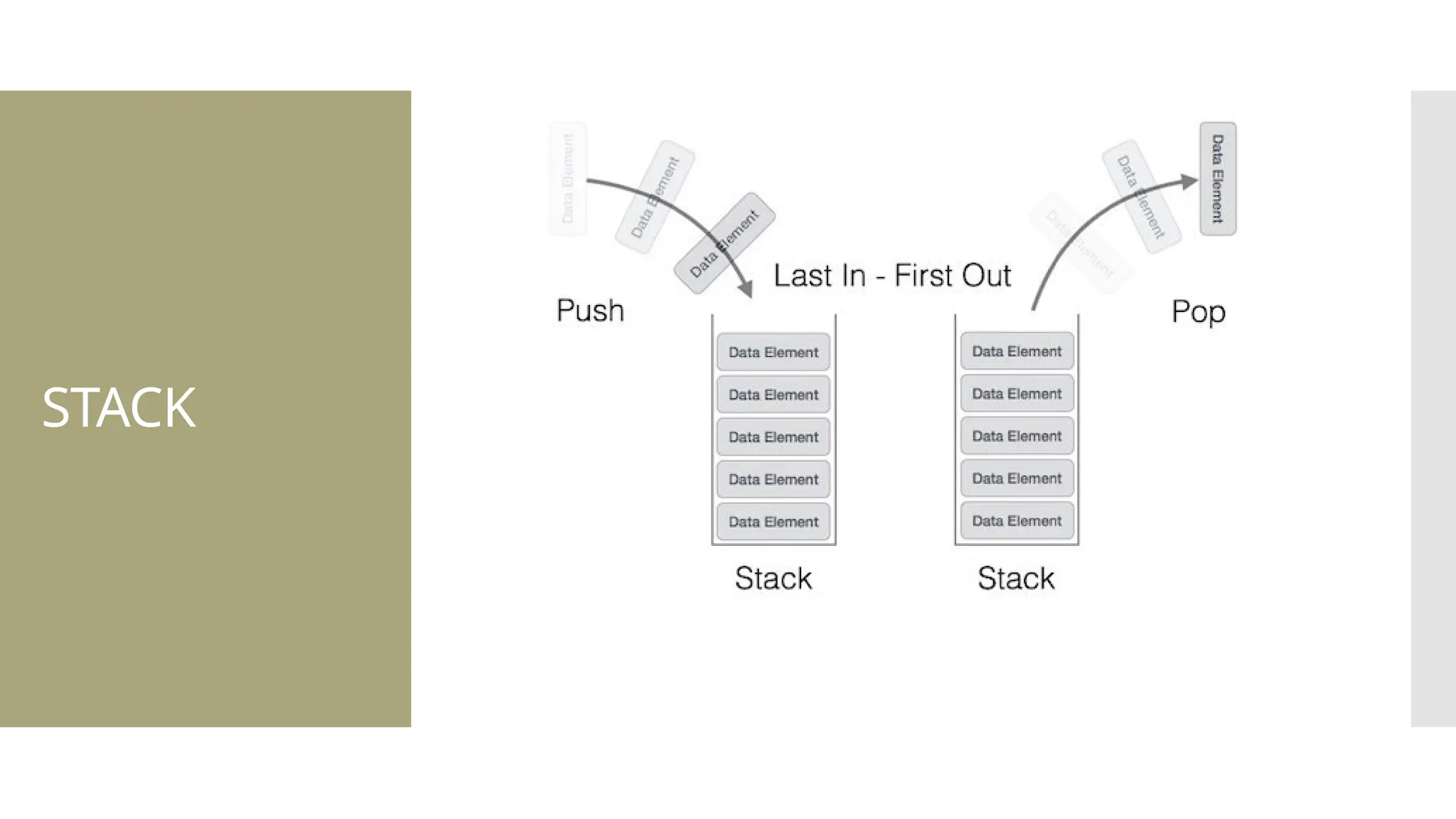
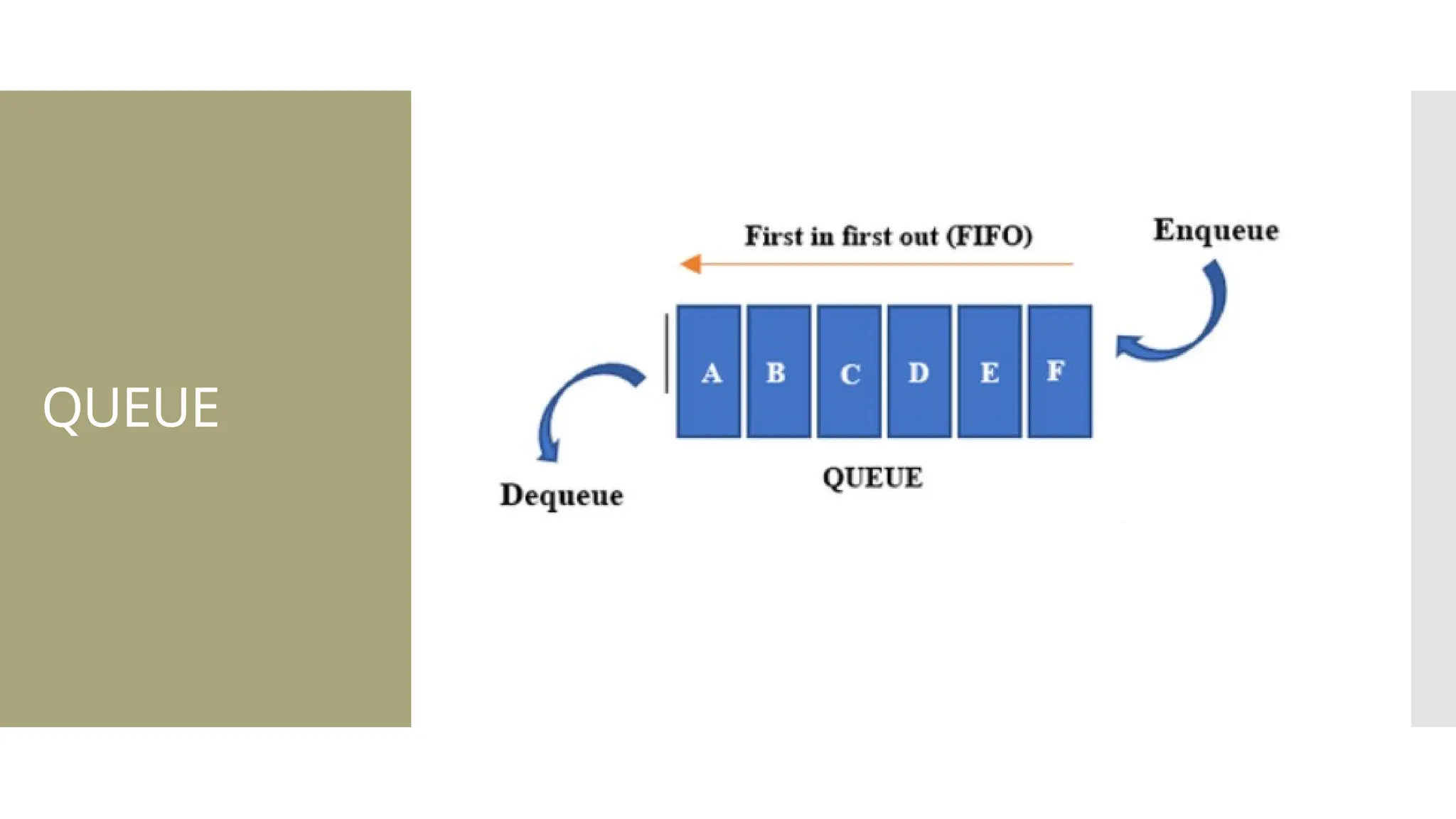
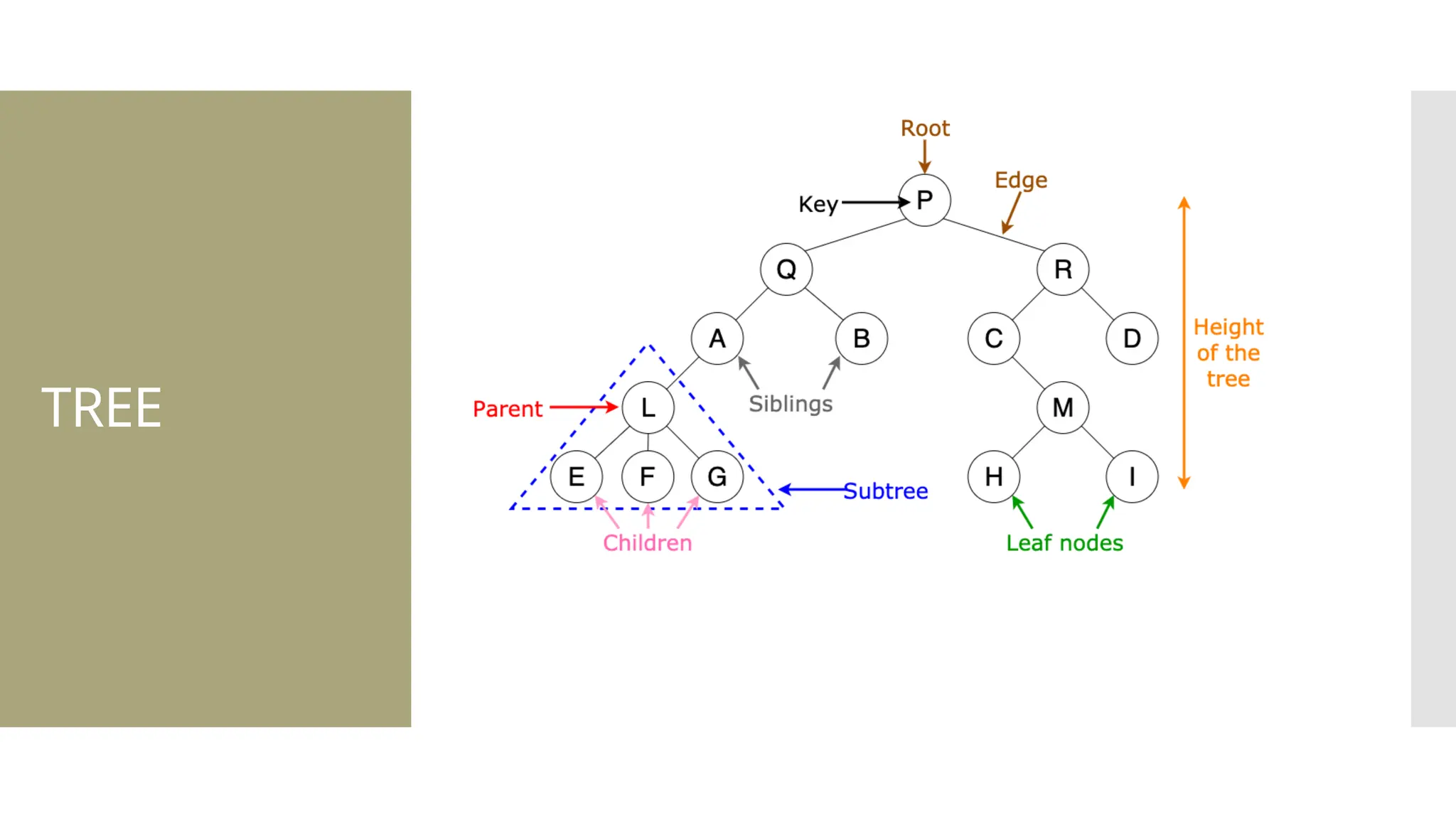
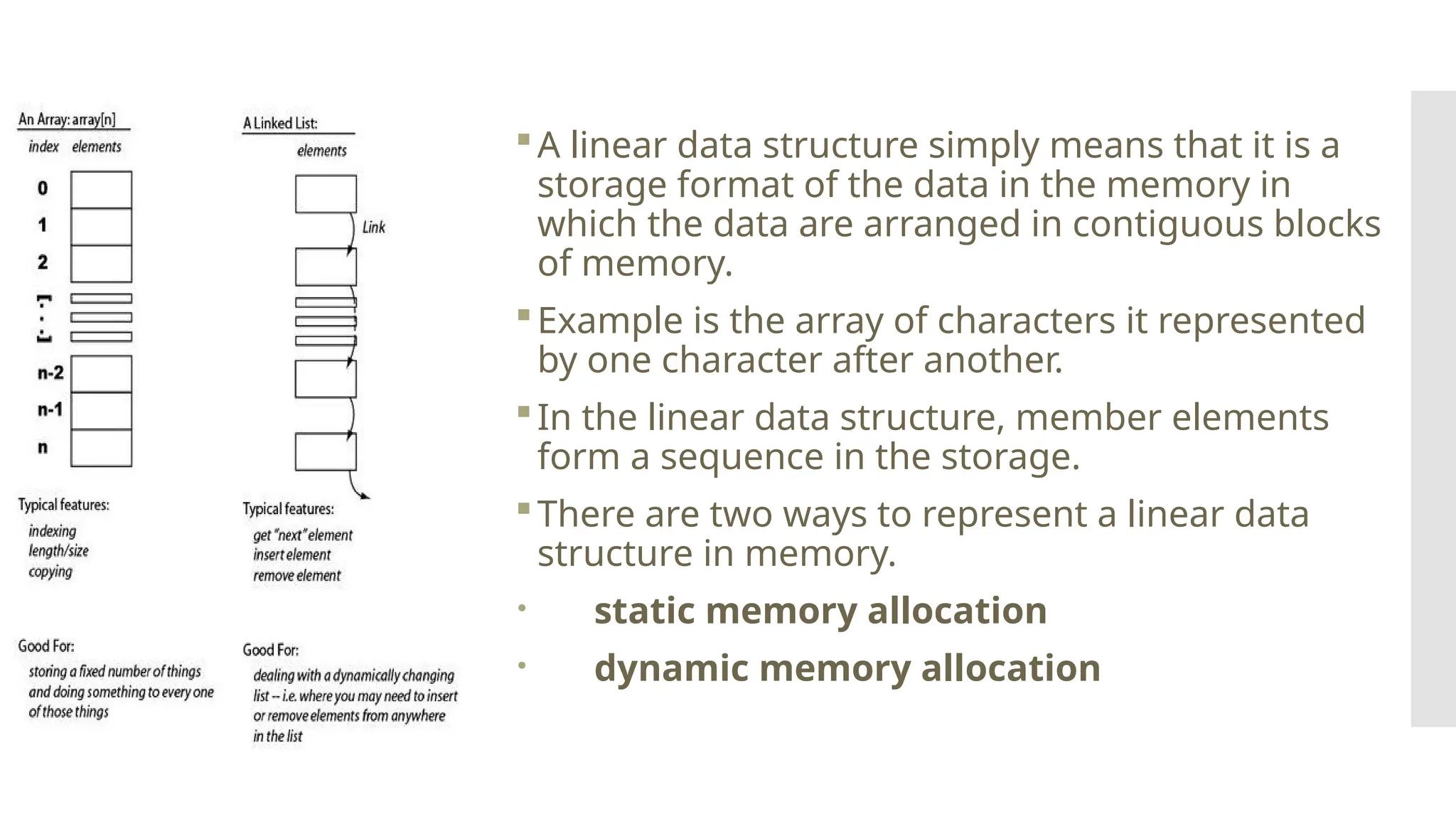
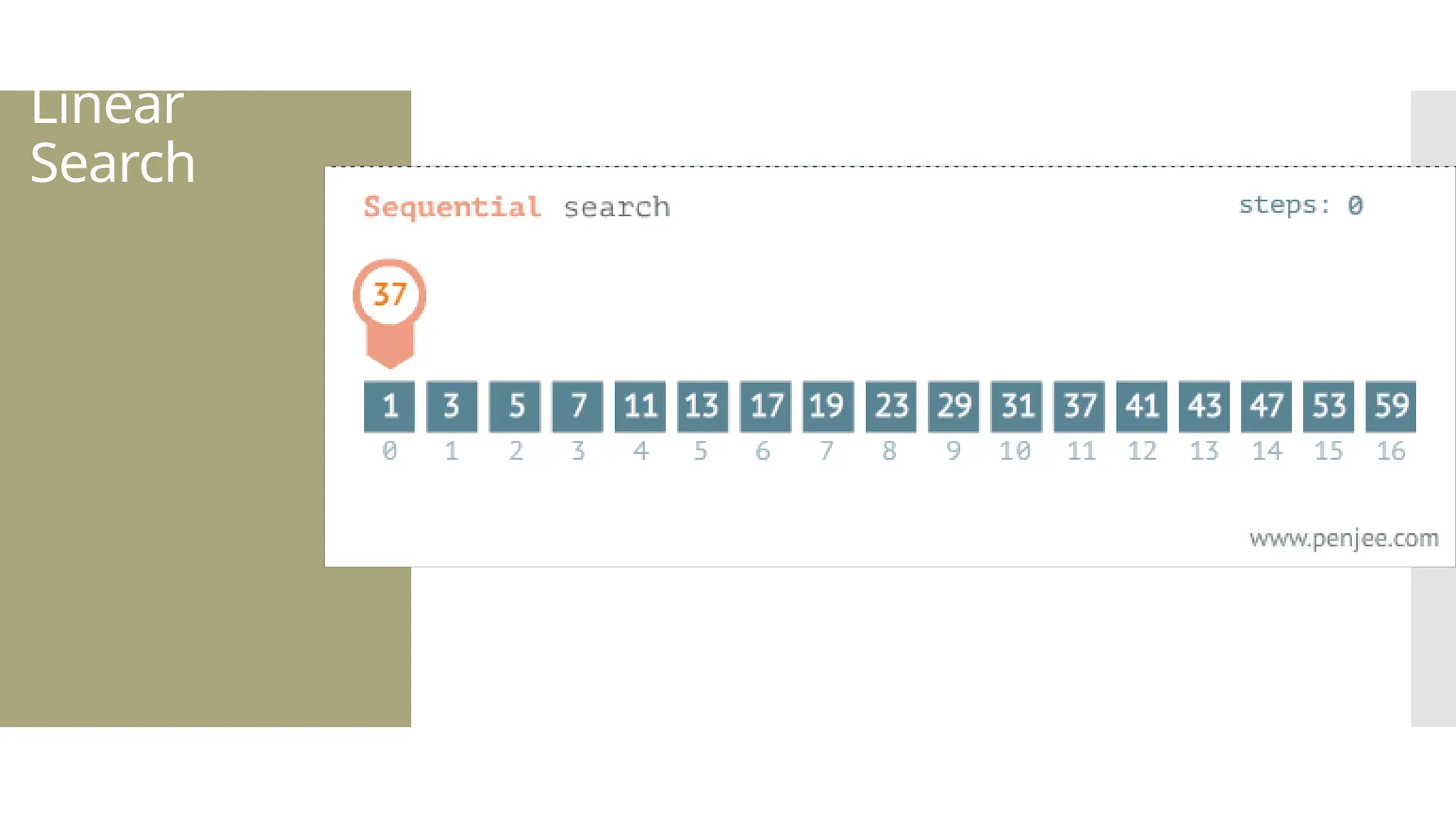
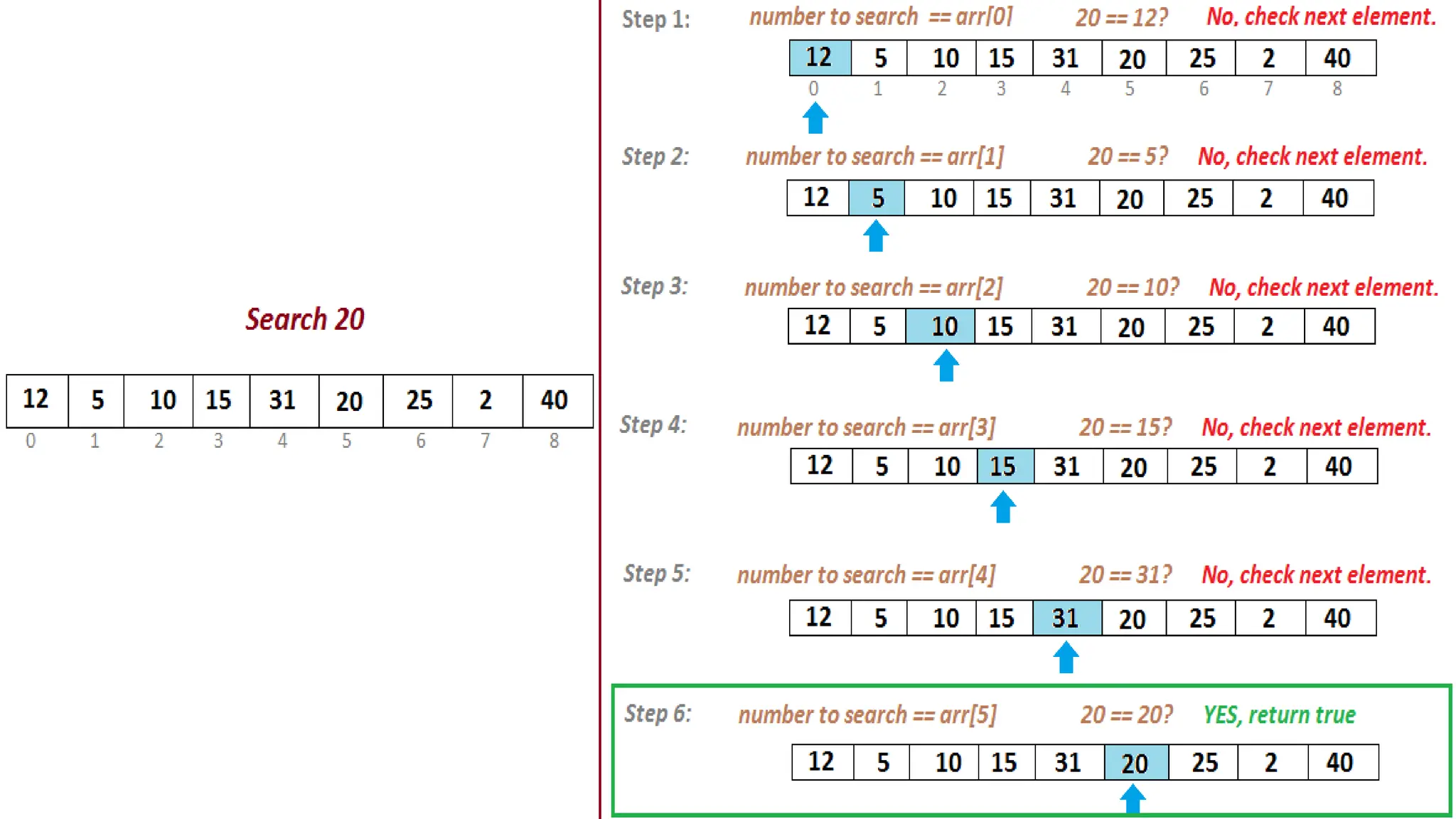
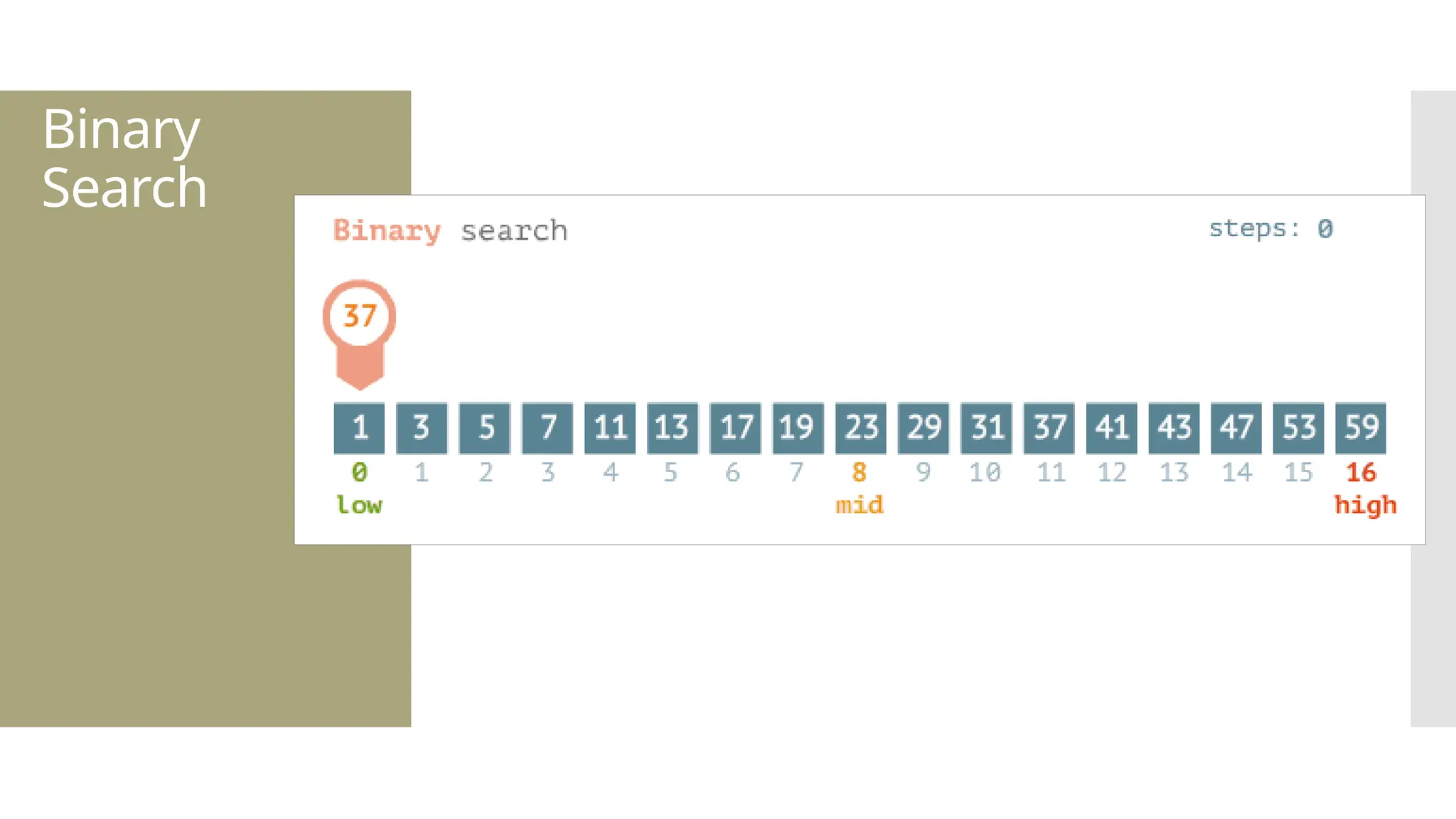
The document provides a comprehensive overview of data structures, including various types such as arrays, linked lists, stacks, queues, trees, and graphs, alongside their applications in programming. It also discusses memory management functions in C, including malloc, calloc, free, and realloc and contrasts the advantages and disadvantages of linked lists versus arrays. Furthermore, it presents algorithms for basic operations on data structures such as insertion, deletion, and sorting methods like quicksort and mergesort.
















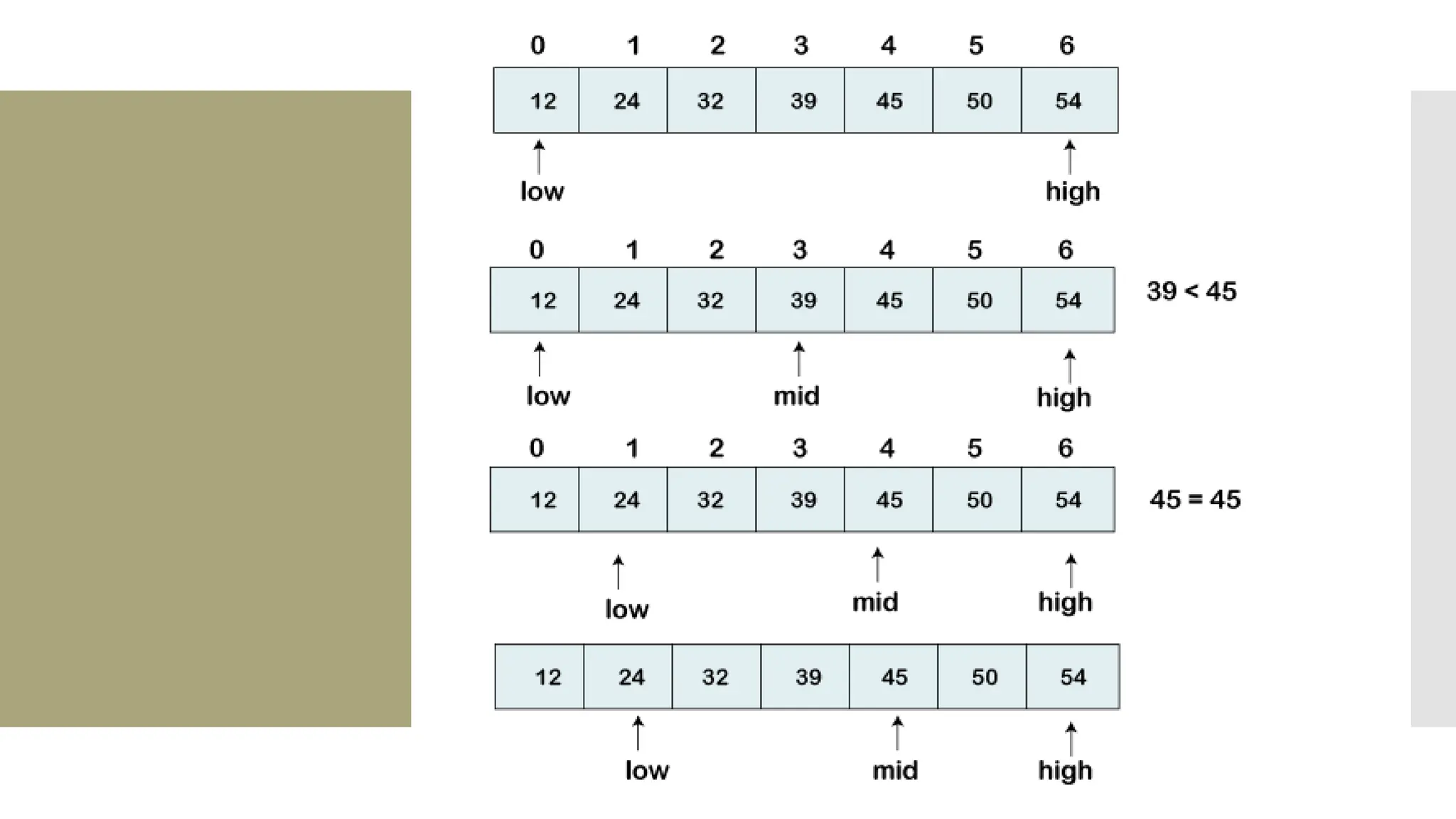
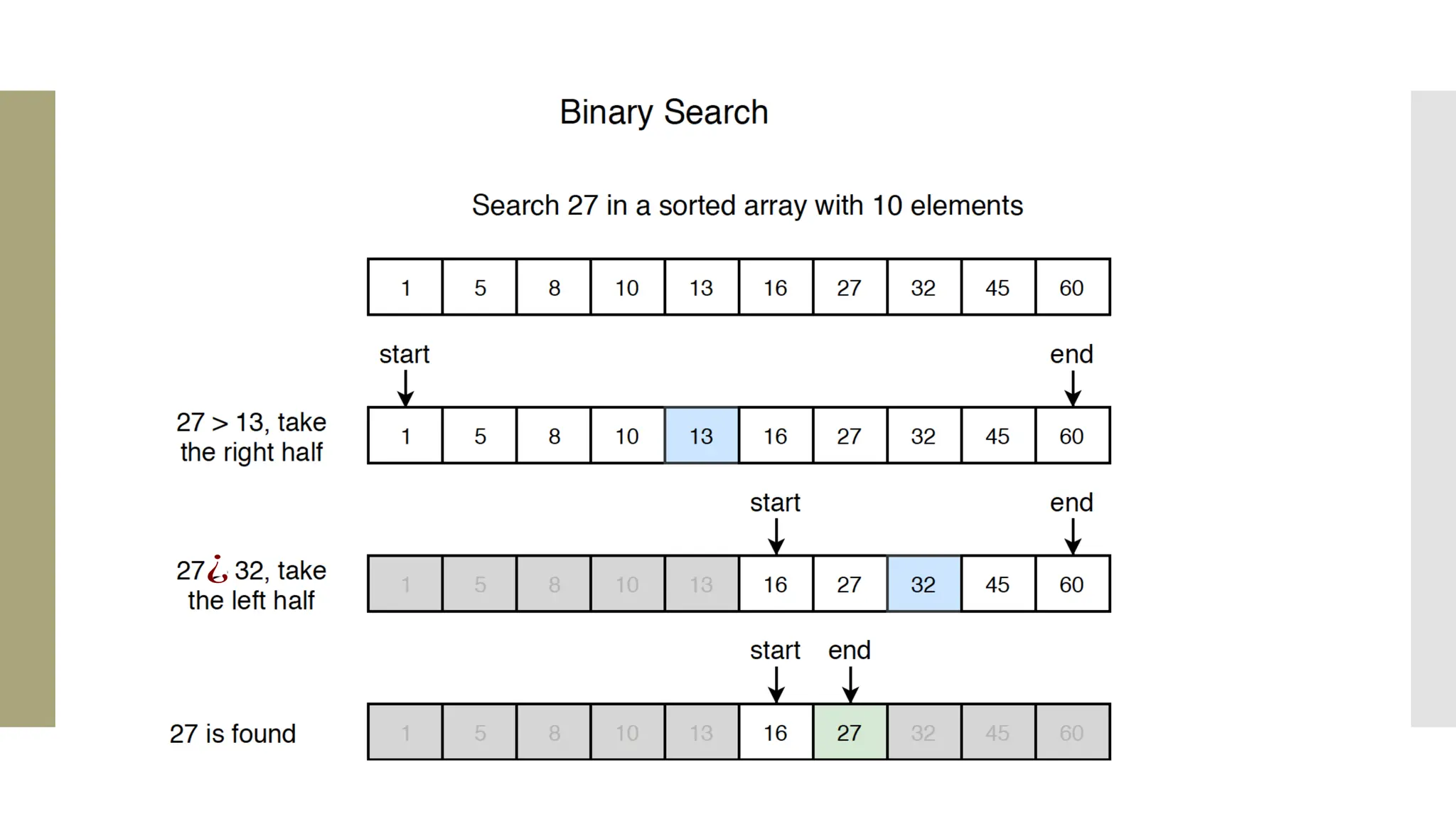

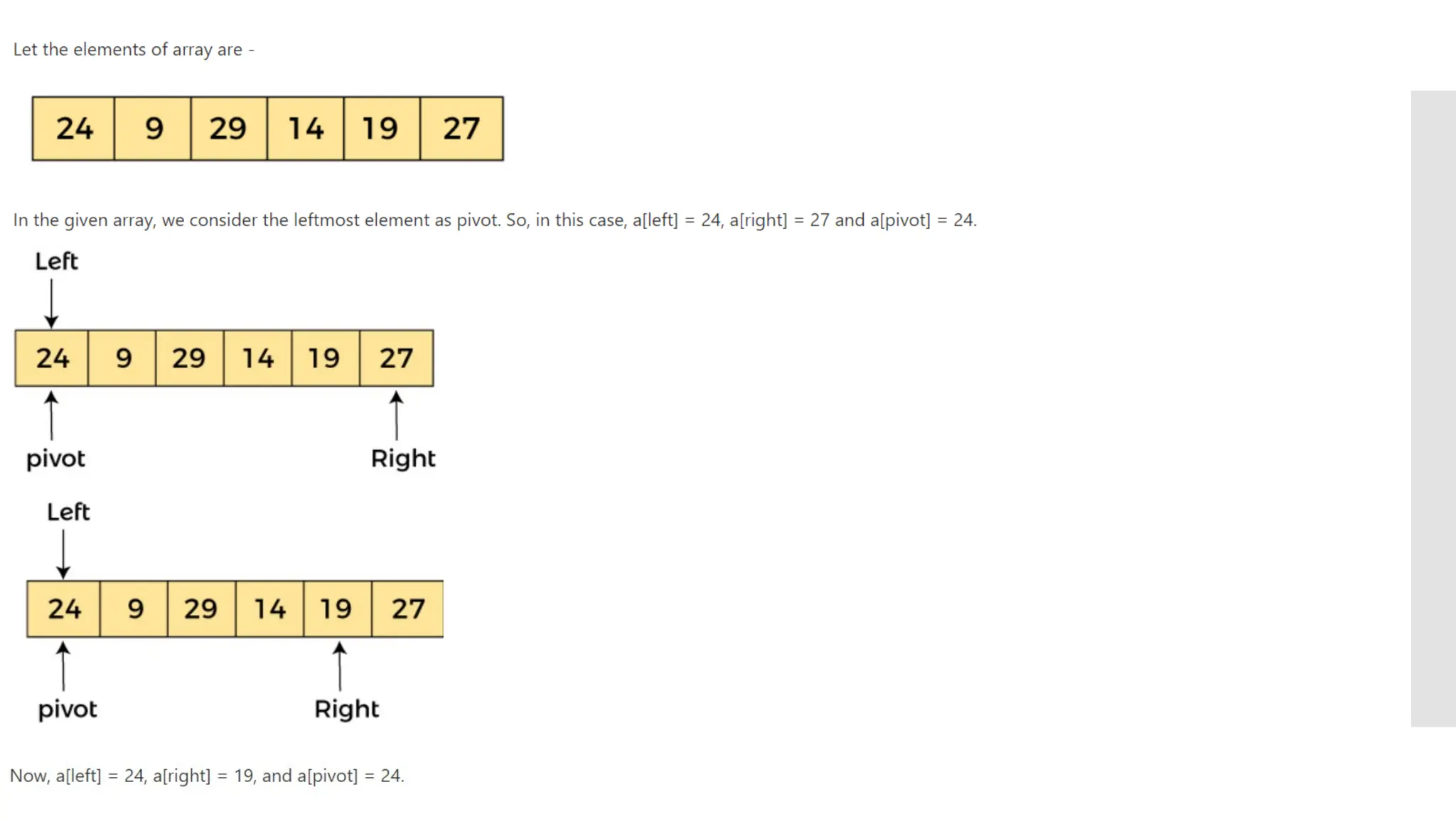
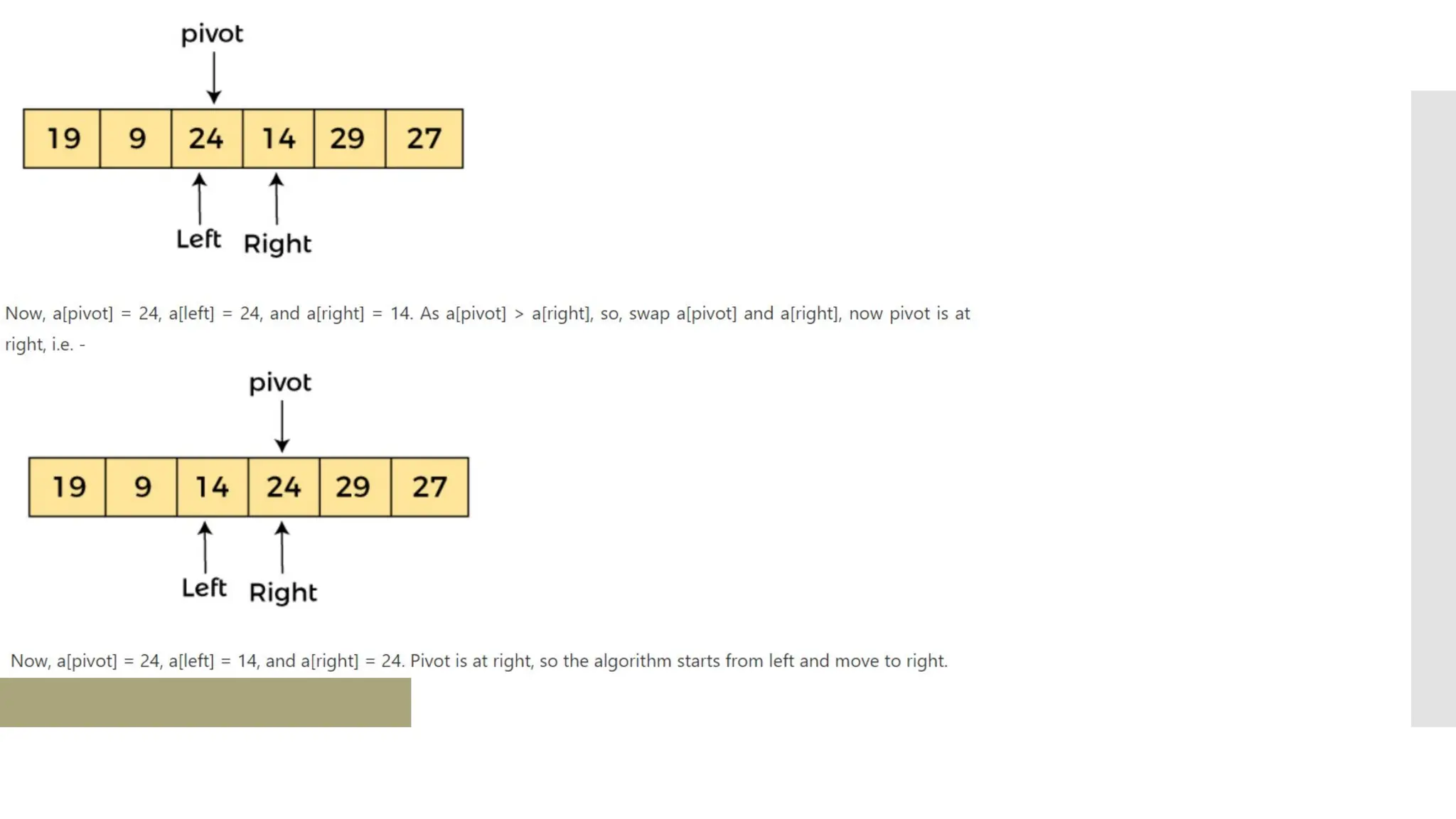
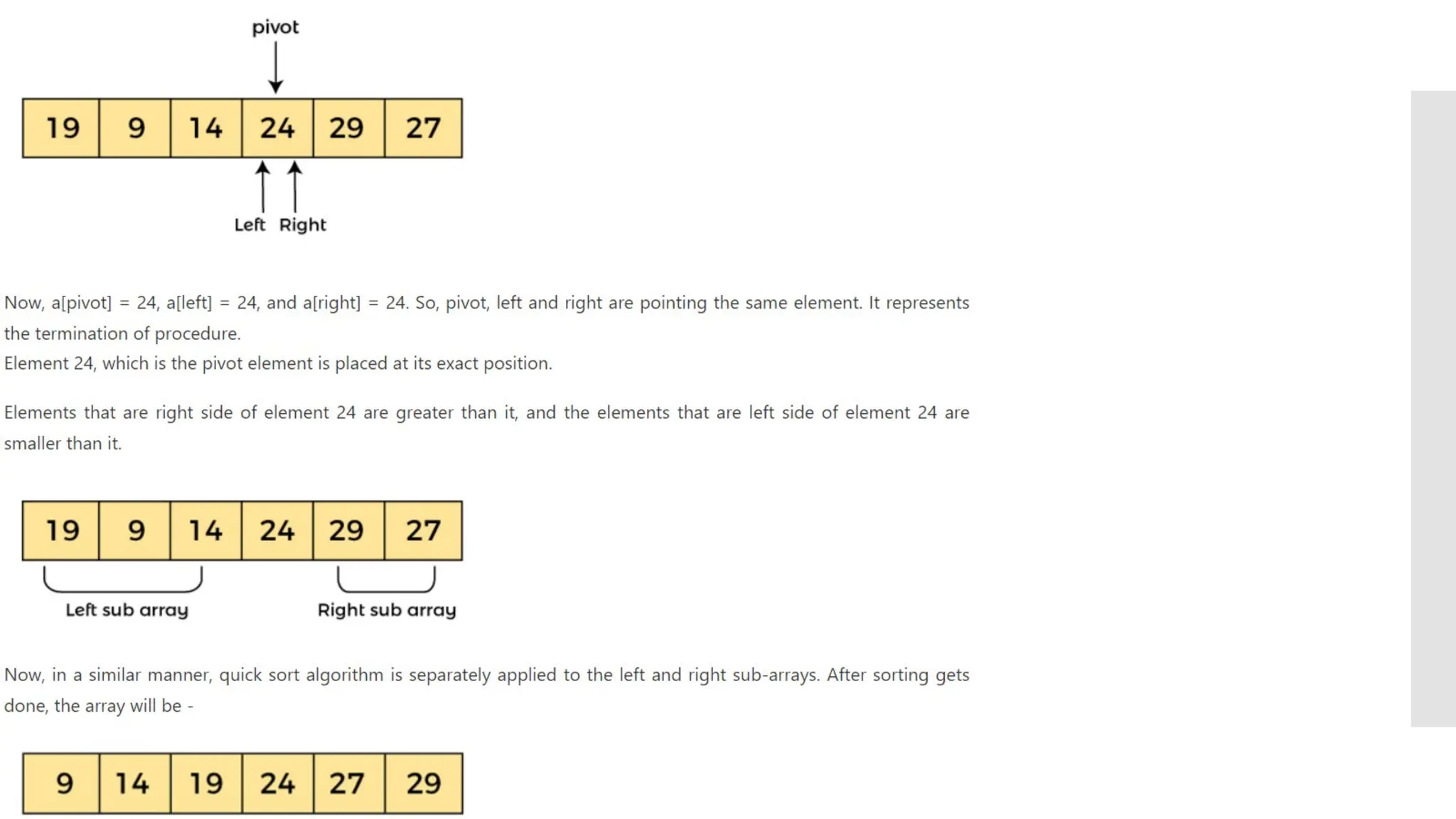
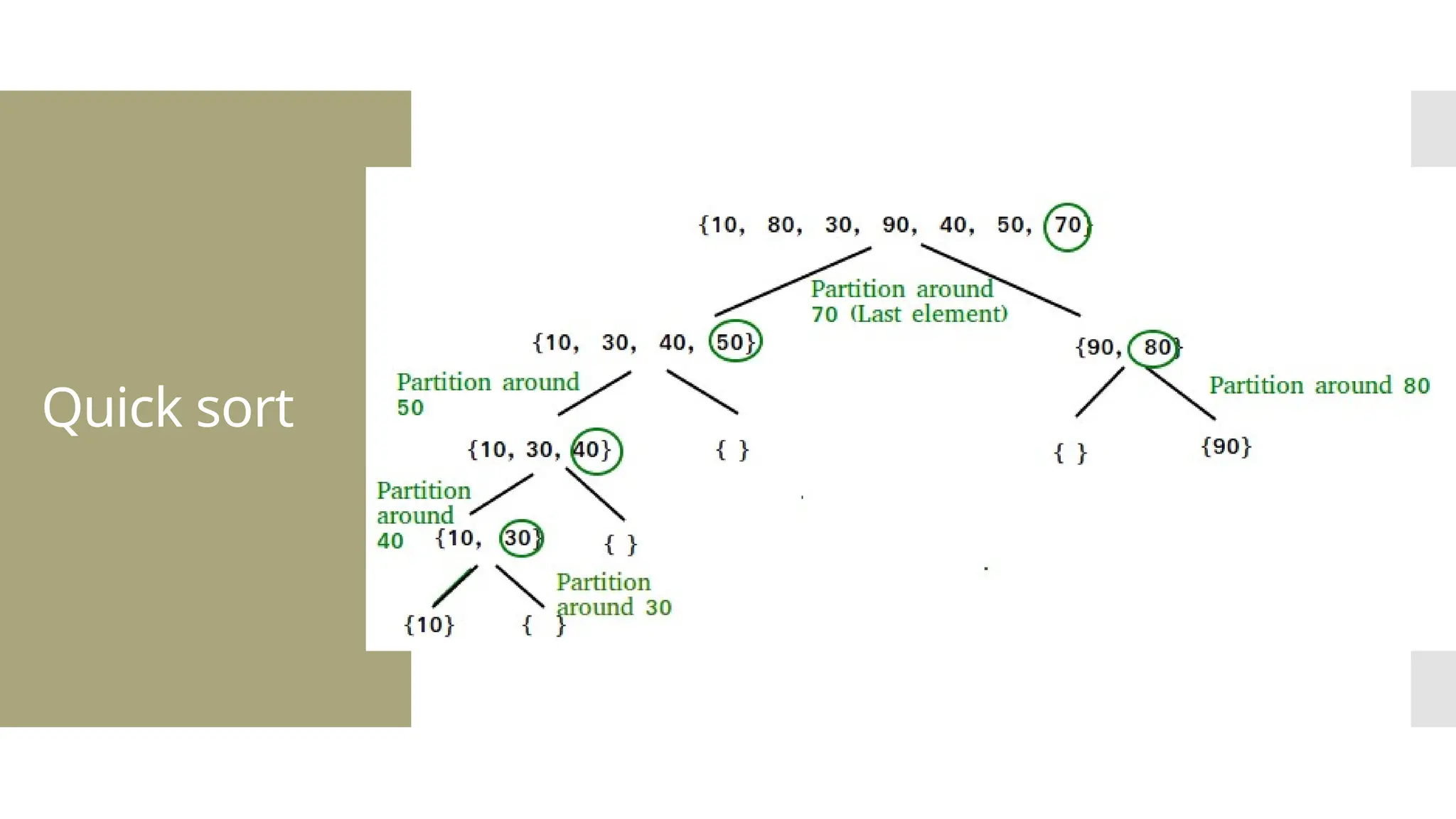
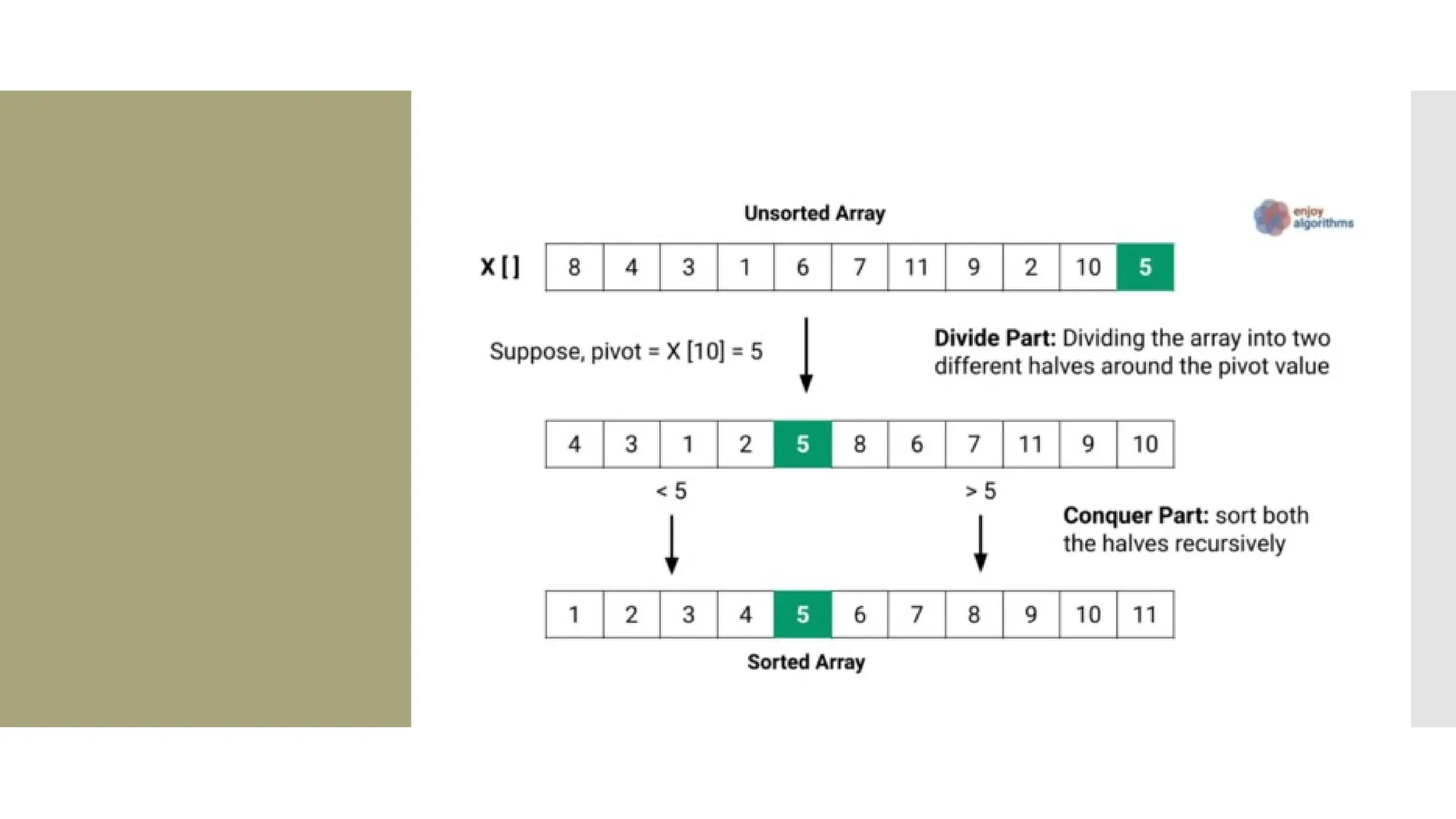
![Steps of quick sort Step by Step Process In Quick sort algorithm, partitioning of the list is performed using following steps... Step 1 - Consider the first element of the list as pivot (i.e., Element at first position in the list). Step 2 - Define two variables i and j. Set i and j to first and last elements of the list respectively. Step 3 - Increment i until list[i] > pivot then stop. Step 4 - Decrement j until list[j] < pivot then stop. Step 5 - If i < j then exchange list[i] and list[j]. Step 6 - Repeat steps 3,4 & 5 until i >= j. Step 7 - Exchange the pivot element with list[j] element.](https://image.slidesharecdn.com/mod1-241127174755-07708fda/75/Introduction-to-data-structures-Explore-the-basics-30-2048.jpg)


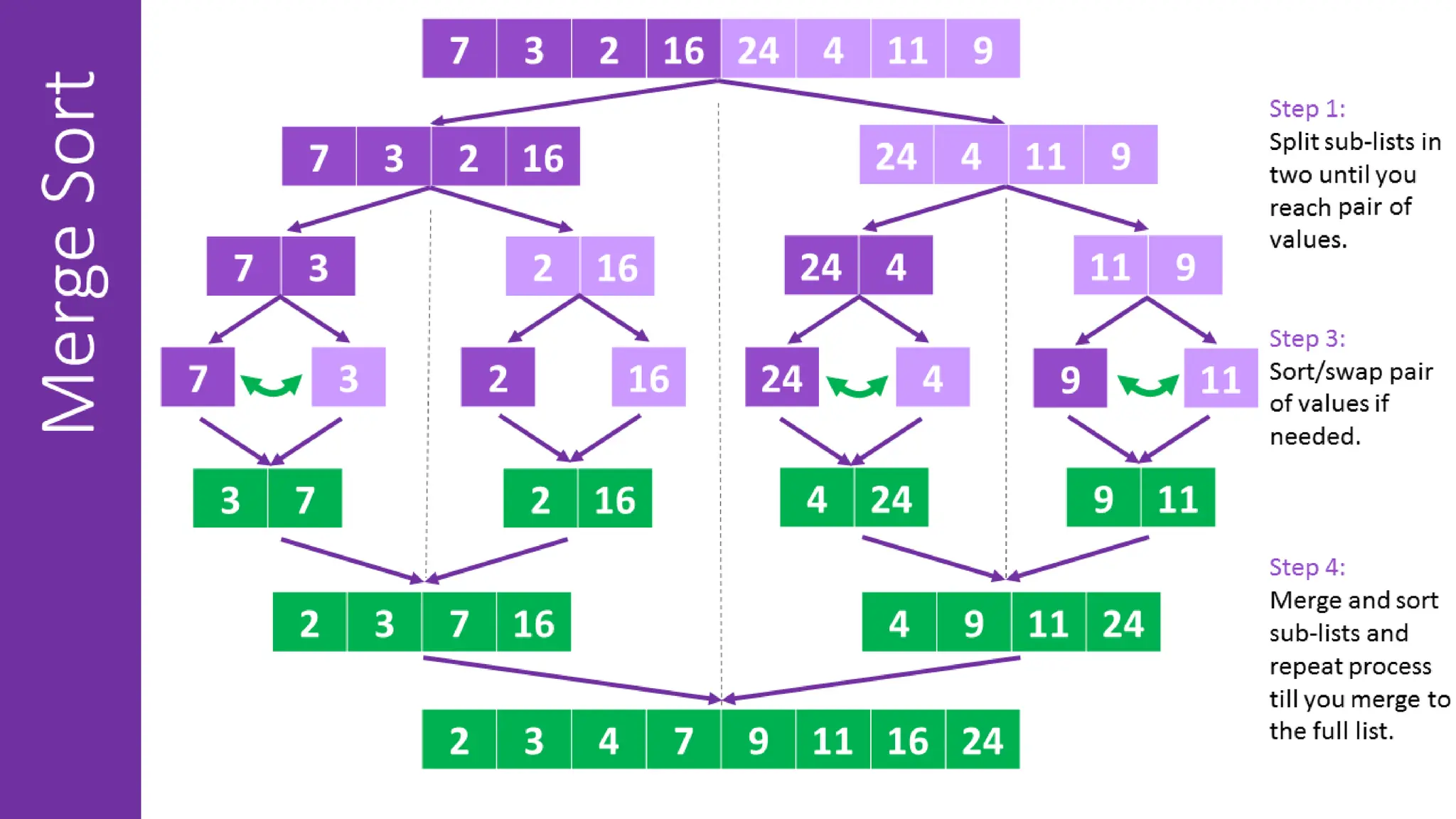

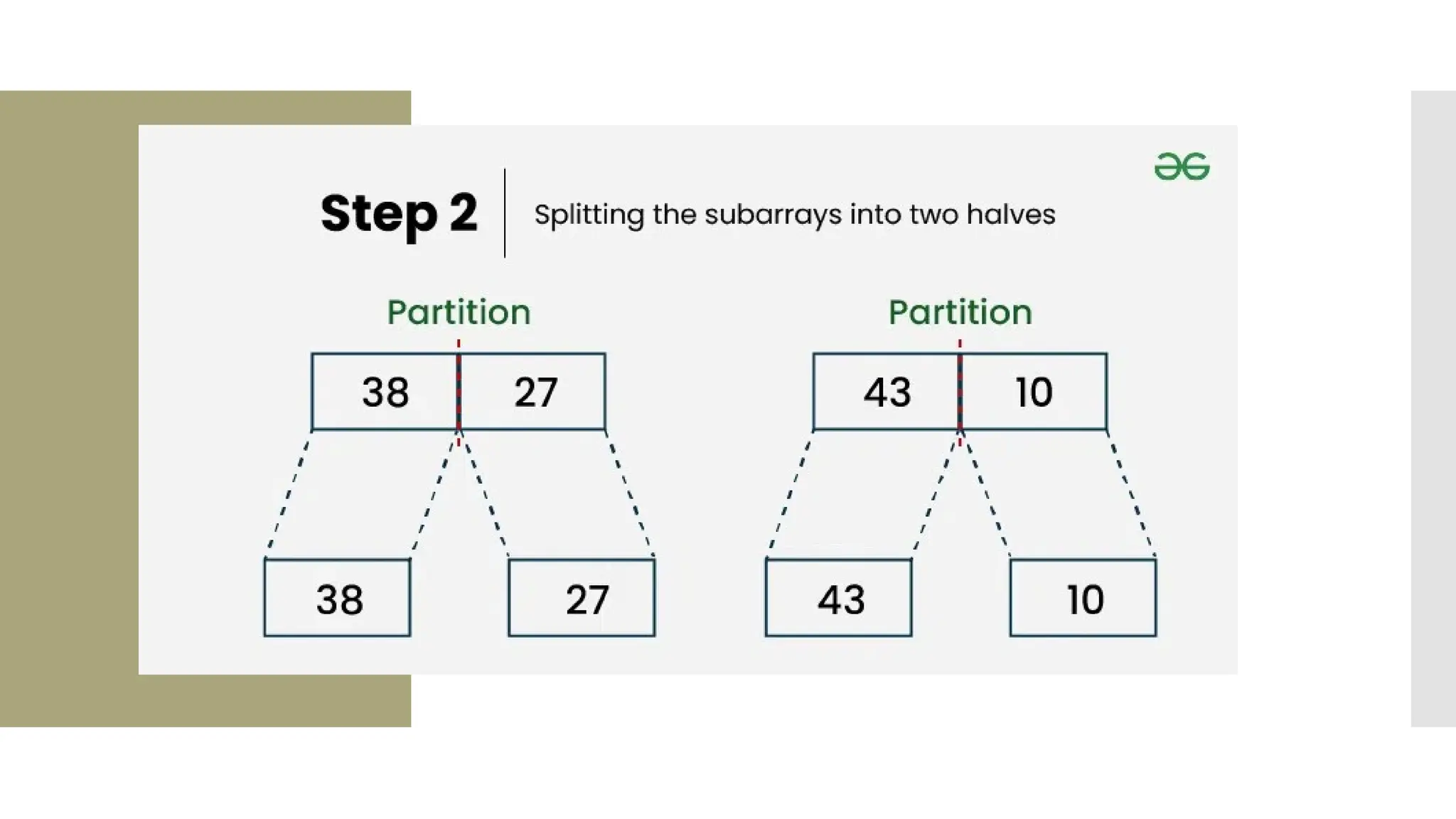
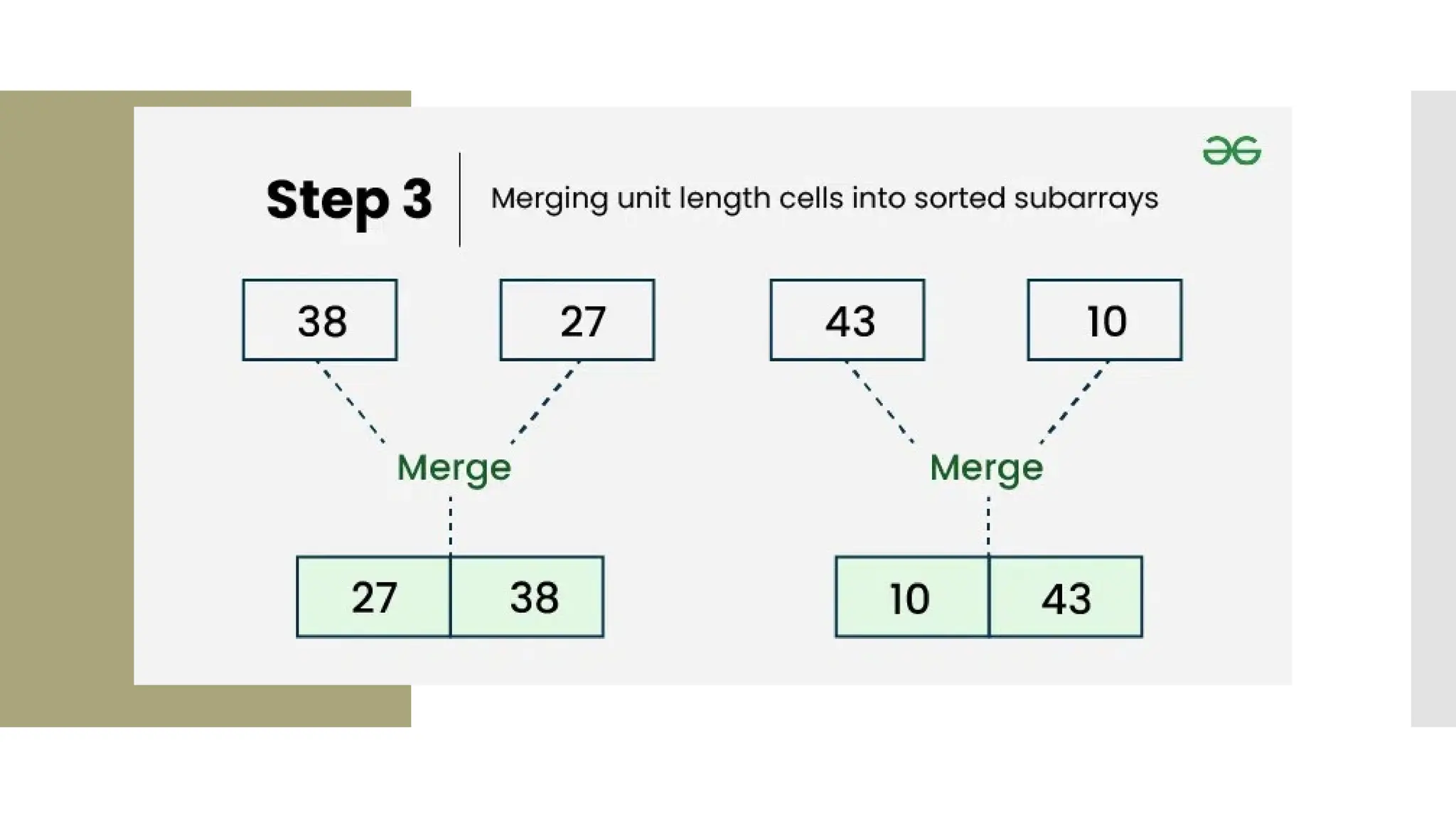
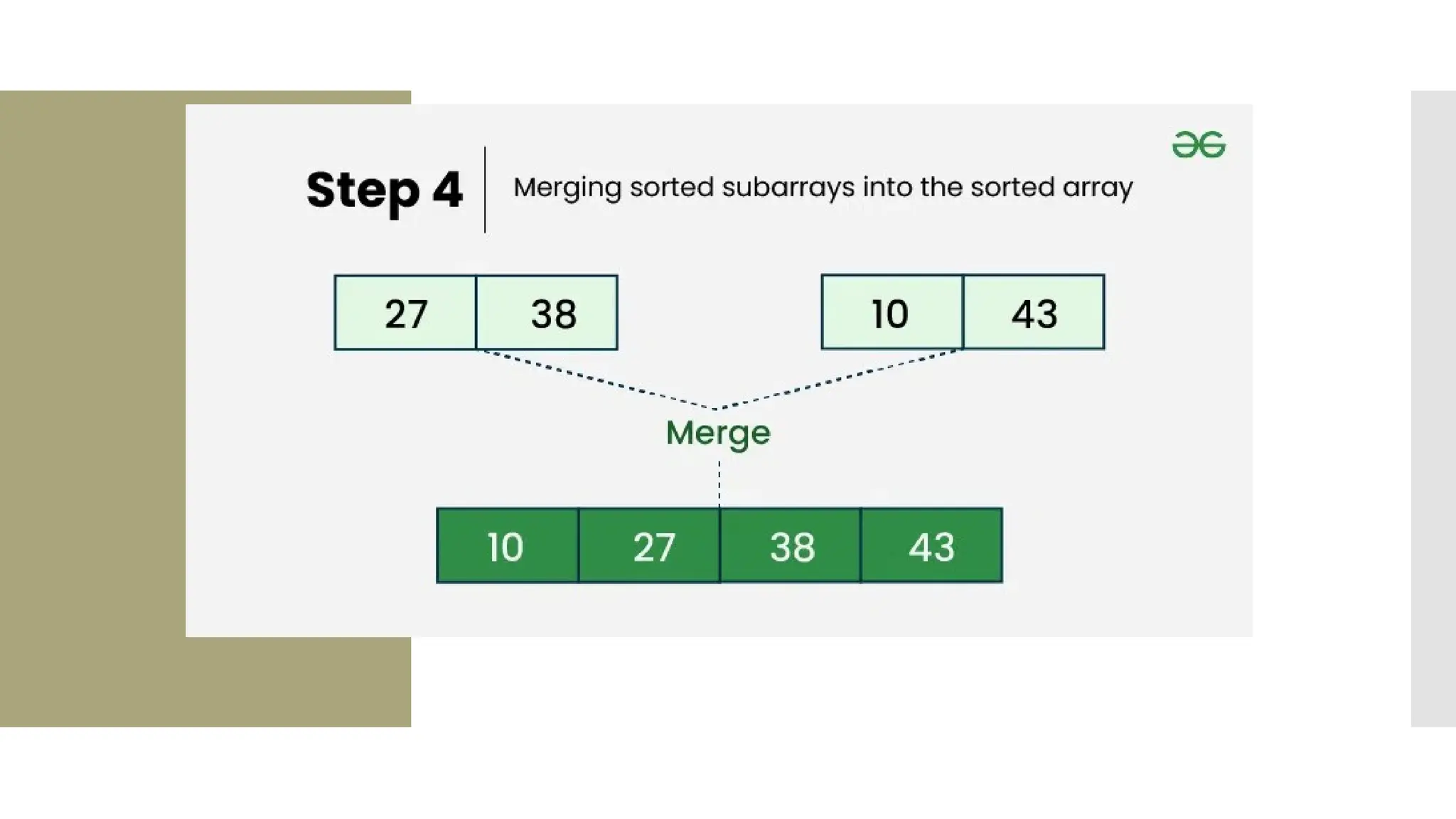
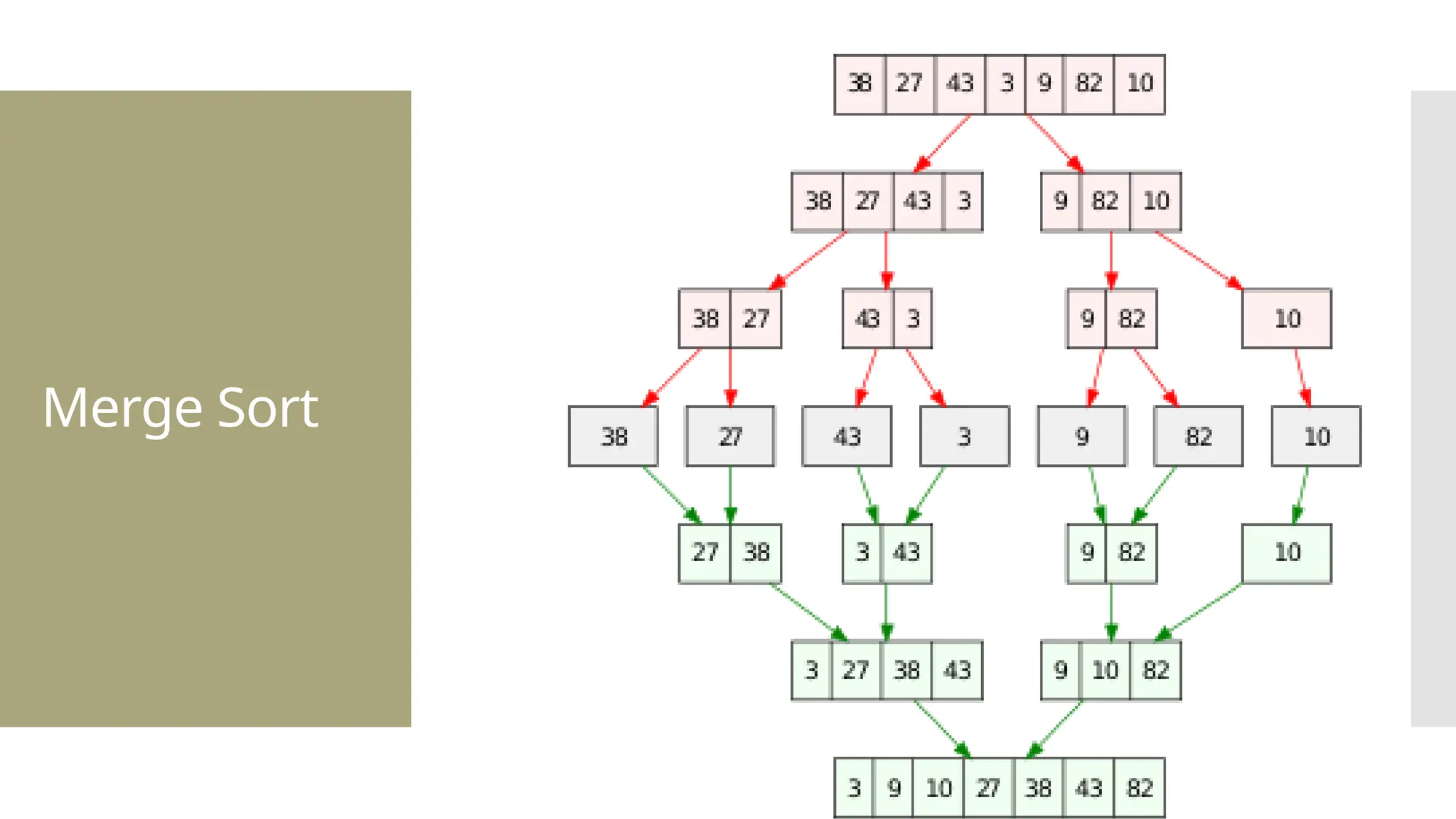
![def mergeSort(arr): if len(arr) <= 1: return arr mid = len(arr) / 2 leftHalf = arr[0:mid] rightHalf = arr[mid:len(arr)] sortedLeft = mergeSort(leftHalf) sortedRight = mergeSort(rightHalf) return merge(sortedLeft, sortedRight)](https://image.slidesharecdn.com/mod1-241127174755-07708fda/75/Introduction-to-data-structures-Explore-the-basics-40-2048.jpg)
![1. def merge(left, right): 2. result = [] 3. i = j = 0 4. while i < len(left) and j < len(right): 5. if left[i] < right[j]: 6. result.append(left[i]) 7. i += 1 8. else: 9. result.append(right[j]) 10. j += 1 11.result.extend(left[i:]) 12. result.extend(right[j:]) 13. return result 14.unsortedArr = [3, 7, 6, - 10, 15, 23.5, 55, -13] 15.sortedArr = mergeSort(unsortedArr) 16.print("Sorted array:", sortedArr)](https://image.slidesharecdn.com/mod1-241127174755-07708fda/75/Introduction-to-data-structures-Explore-the-basics-41-2048.jpg)





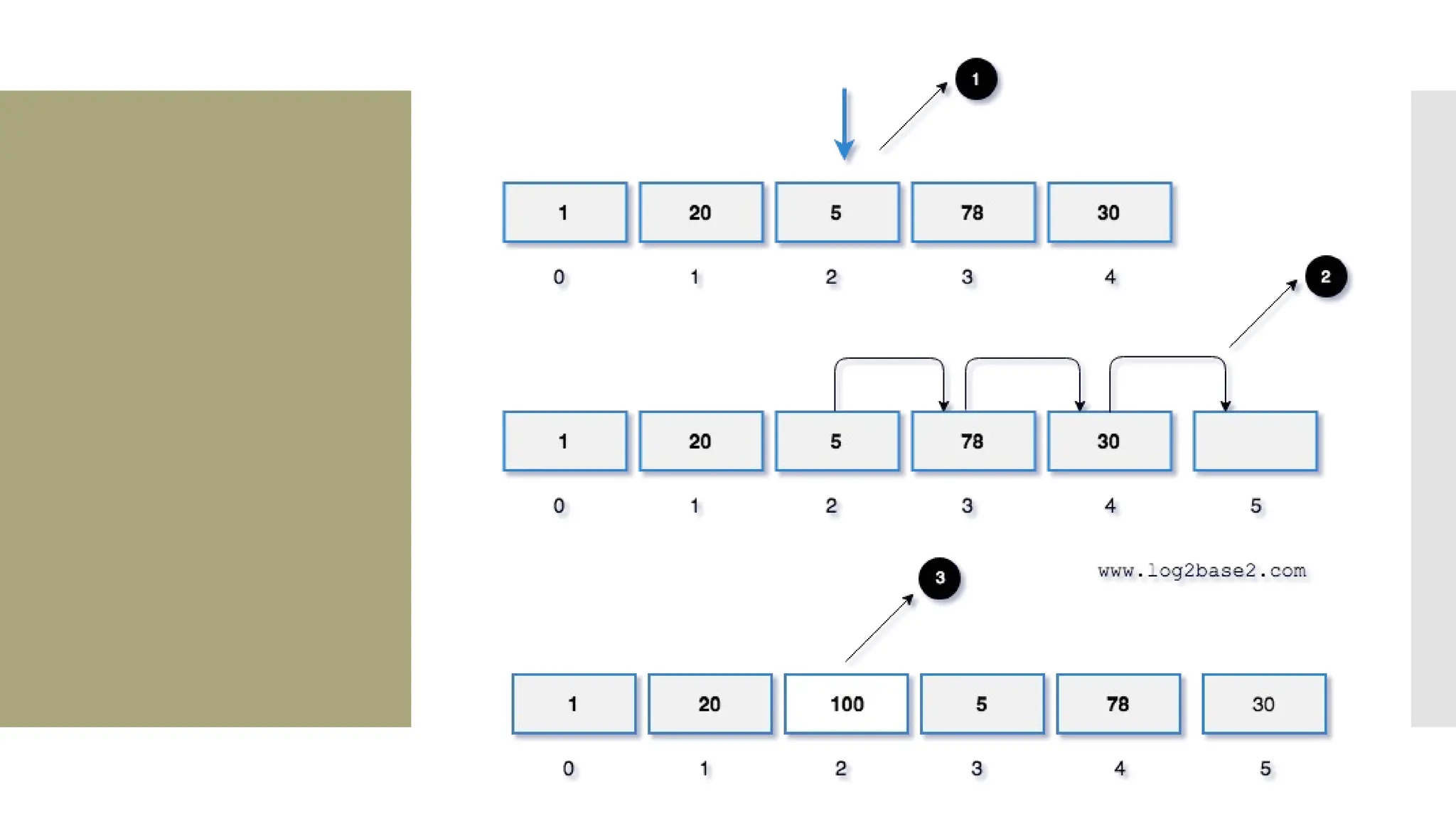
![Insert an element Algorithm InsertLA (DATA, N, ITEM, LOC) Desc: This algorithm inserts new element ITEM in linear array DATA with N elements If LOC=1 it means the element has to insert in beginning If LOC =N+1 it means the element have to be inserted at the end If LOC = J it means the elements have to be inserted at Jth Location Begin Step 1: [Initialize counter I with index of last element] I=N Step 2: While I >=LOC repeat steps 3 and 4 Step 3: [Move the current element one position backwards] DATA[I+1]=DATA[I] Step 4: [Decrement counter I] I=I-1 Step 5:[Insert new element at the Location] DATA[LOC]=ITEM Step 6:[ Update total under of array elements] N=N+1 Exit](https://image.slidesharecdn.com/mod1-241127174755-07708fda/75/Introduction-to-data-structures-Explore-the-basics-52-2048.jpg)
![ It is a process of deleting a particular element from an array. If an element to be deleted ith location then all elements from the (i+1)th location we have to be shifted one step towards left. So (i+1)th element is copied to ith location and (i+2)th to (i+1)th location and so on. Algorithm: In this algorithm a value is being deleted from ith location of an array Reg[N]. Let us assume that last element in the array is at Mth position. Steps 1. Back=i 2. While (Back<M) repeat 3 and 4 3. Reg[Back]= Reg[Back+1] 4. Back= Back+1 5. M=M-1 6. End](https://image.slidesharecdn.com/mod1-241127174755-07708fda/75/Introduction-to-data-structures-Explore-the-basics-53-2048.jpg)