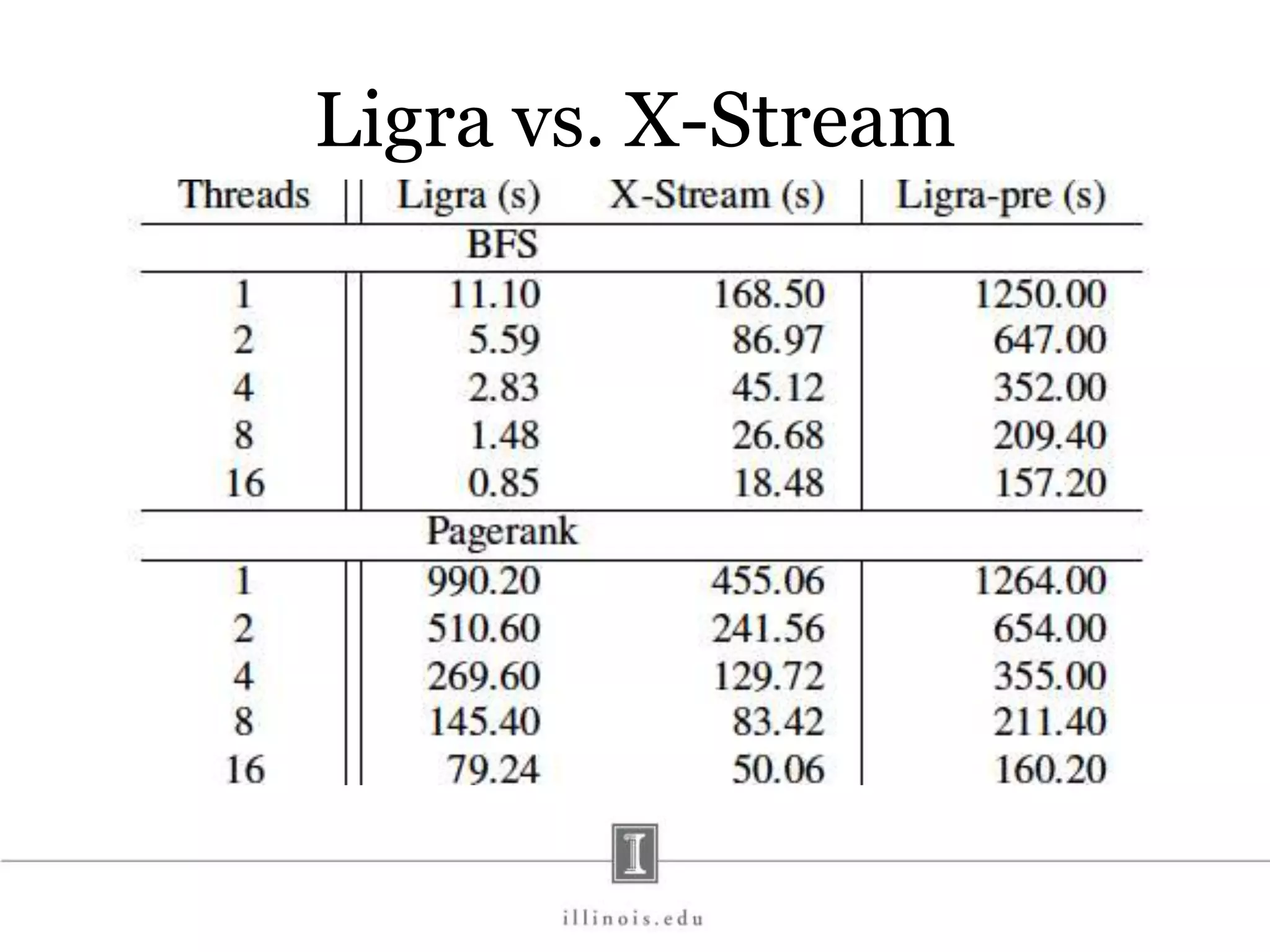
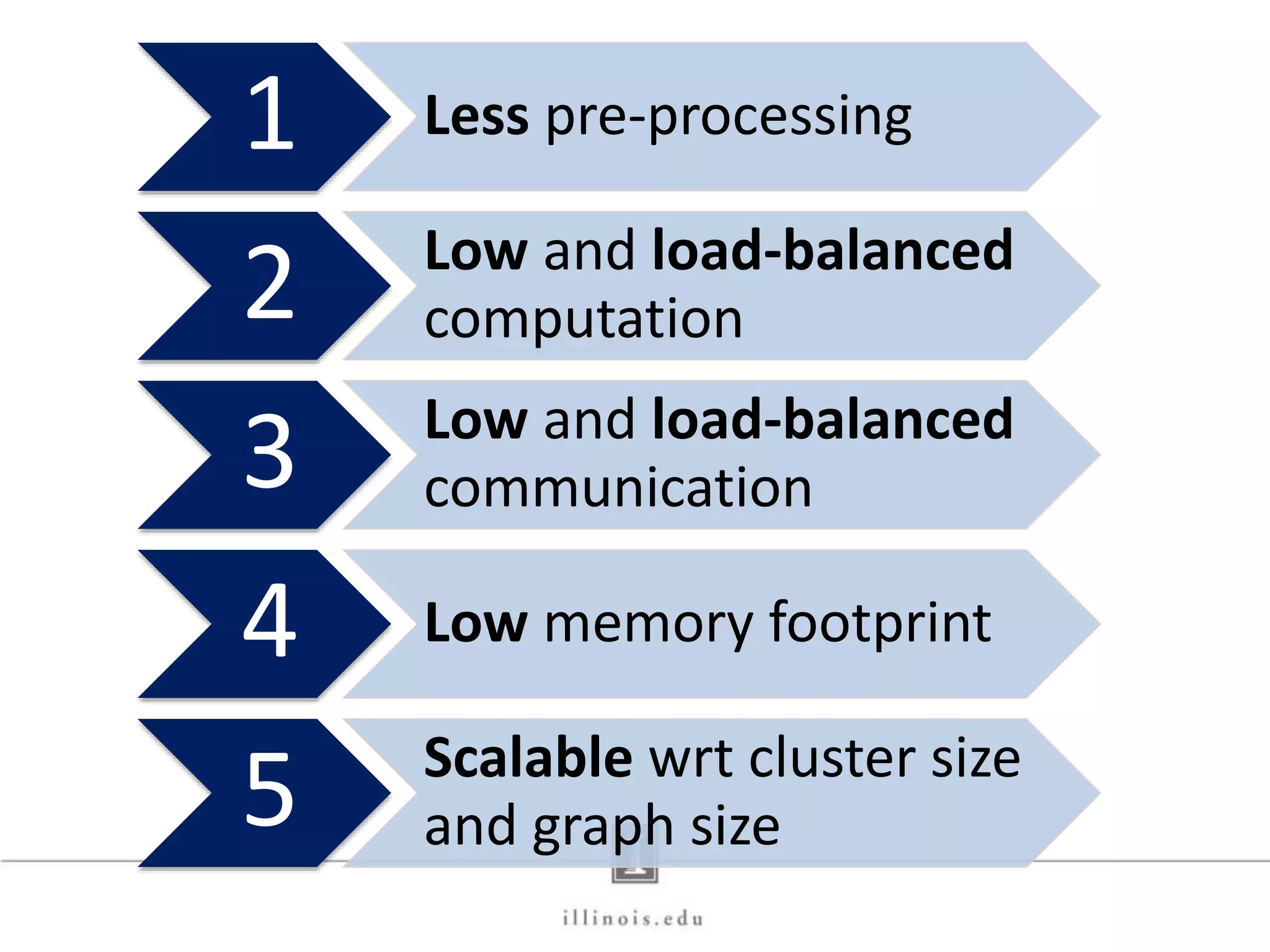
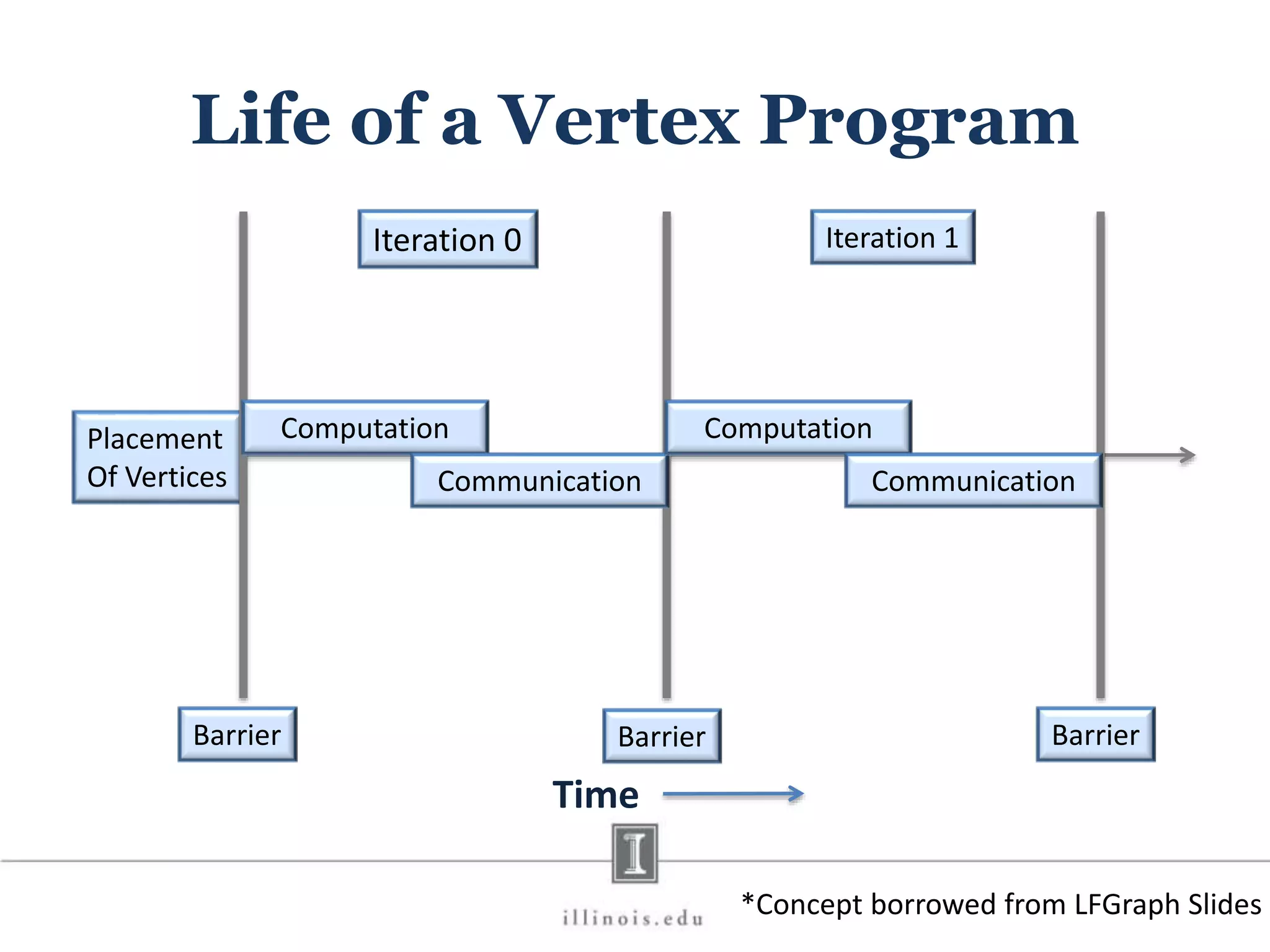
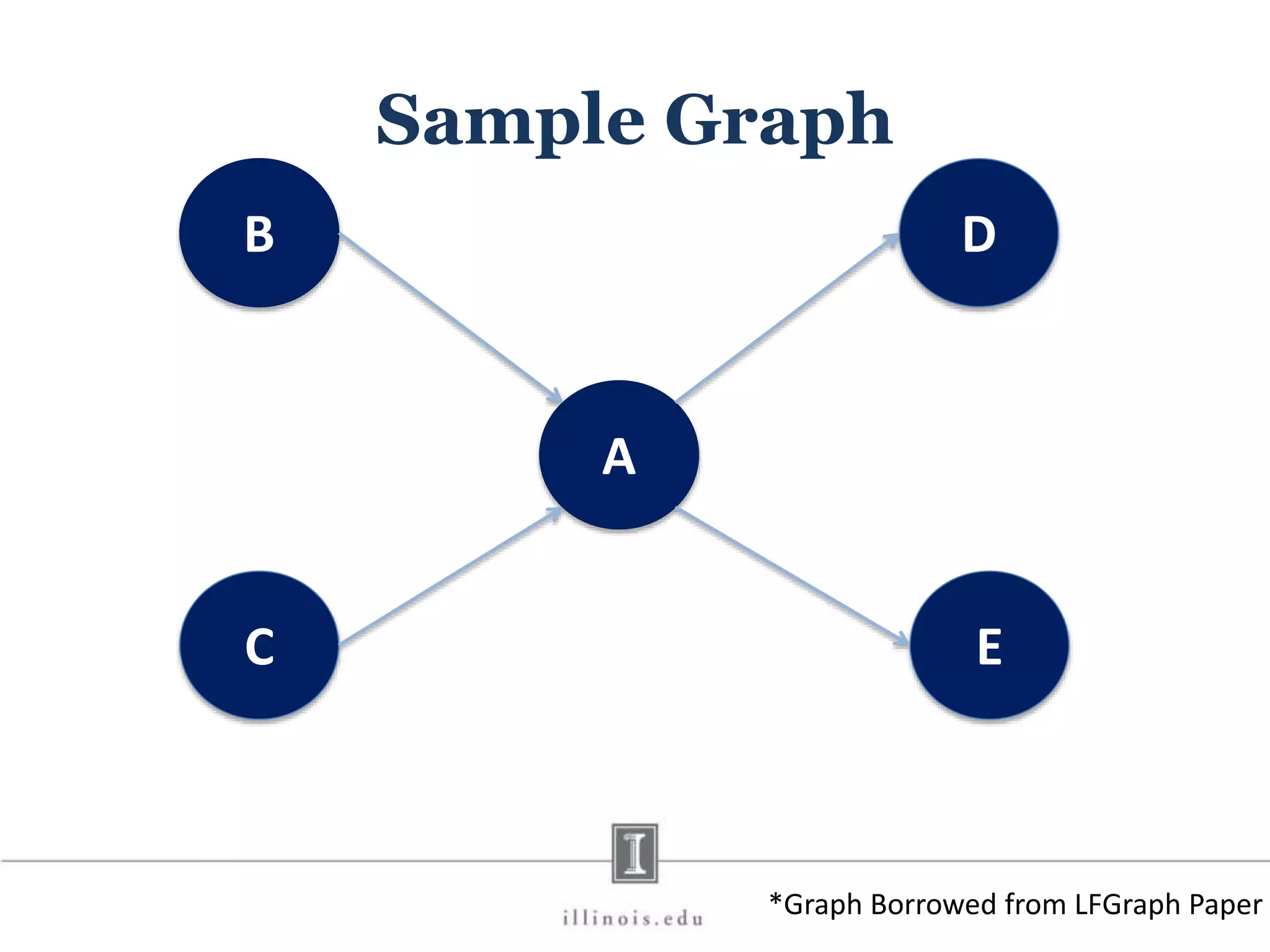
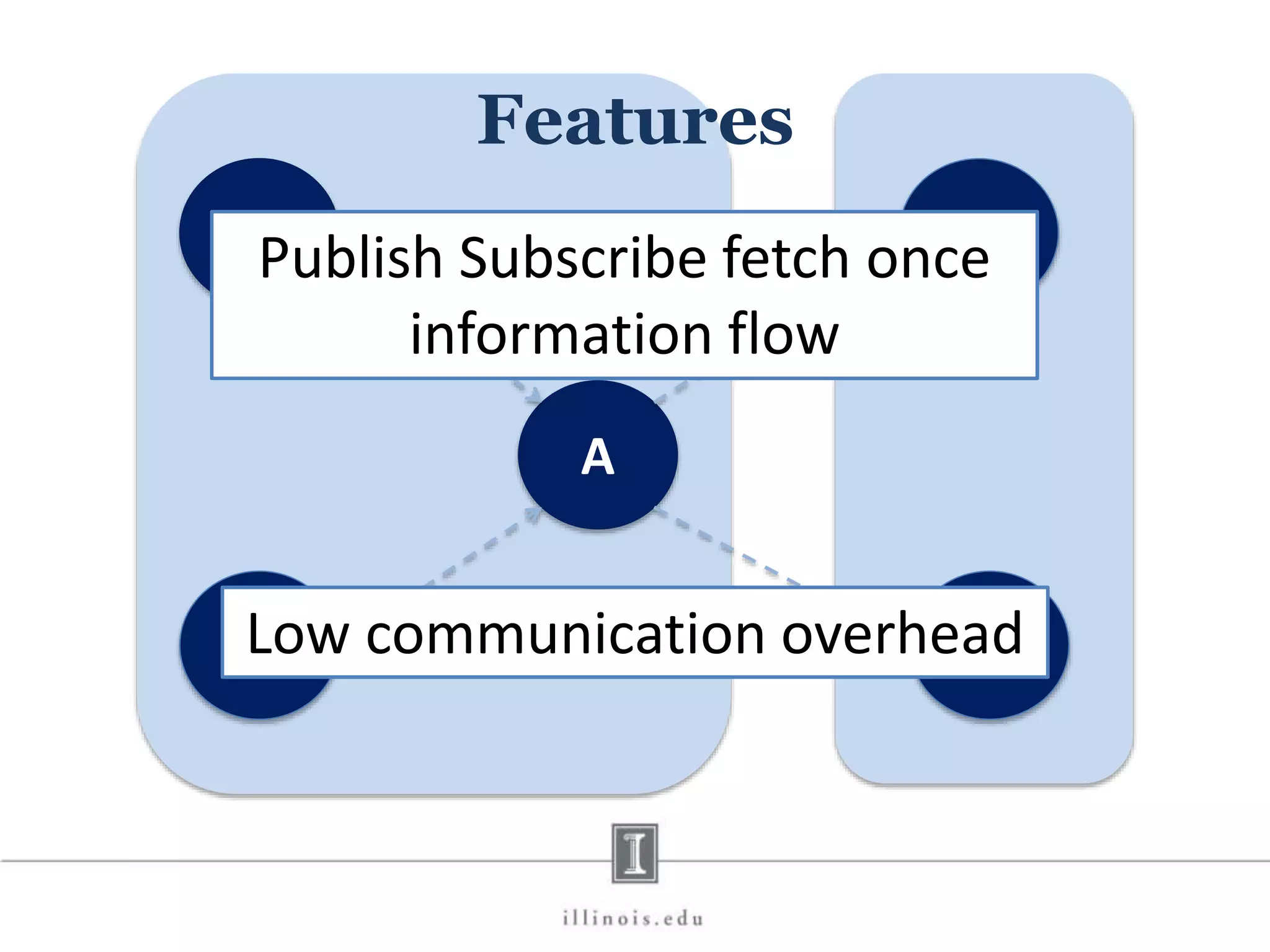
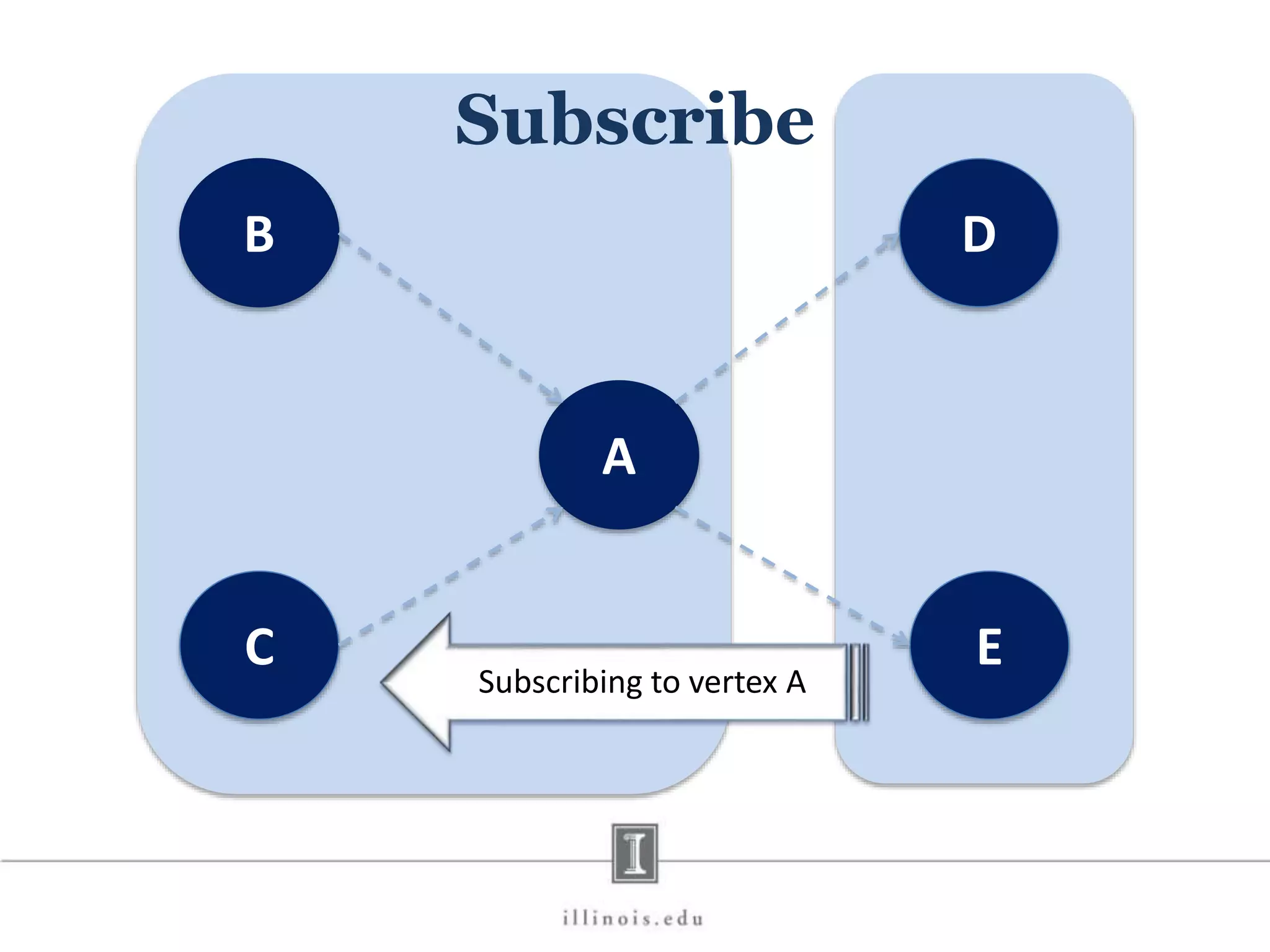
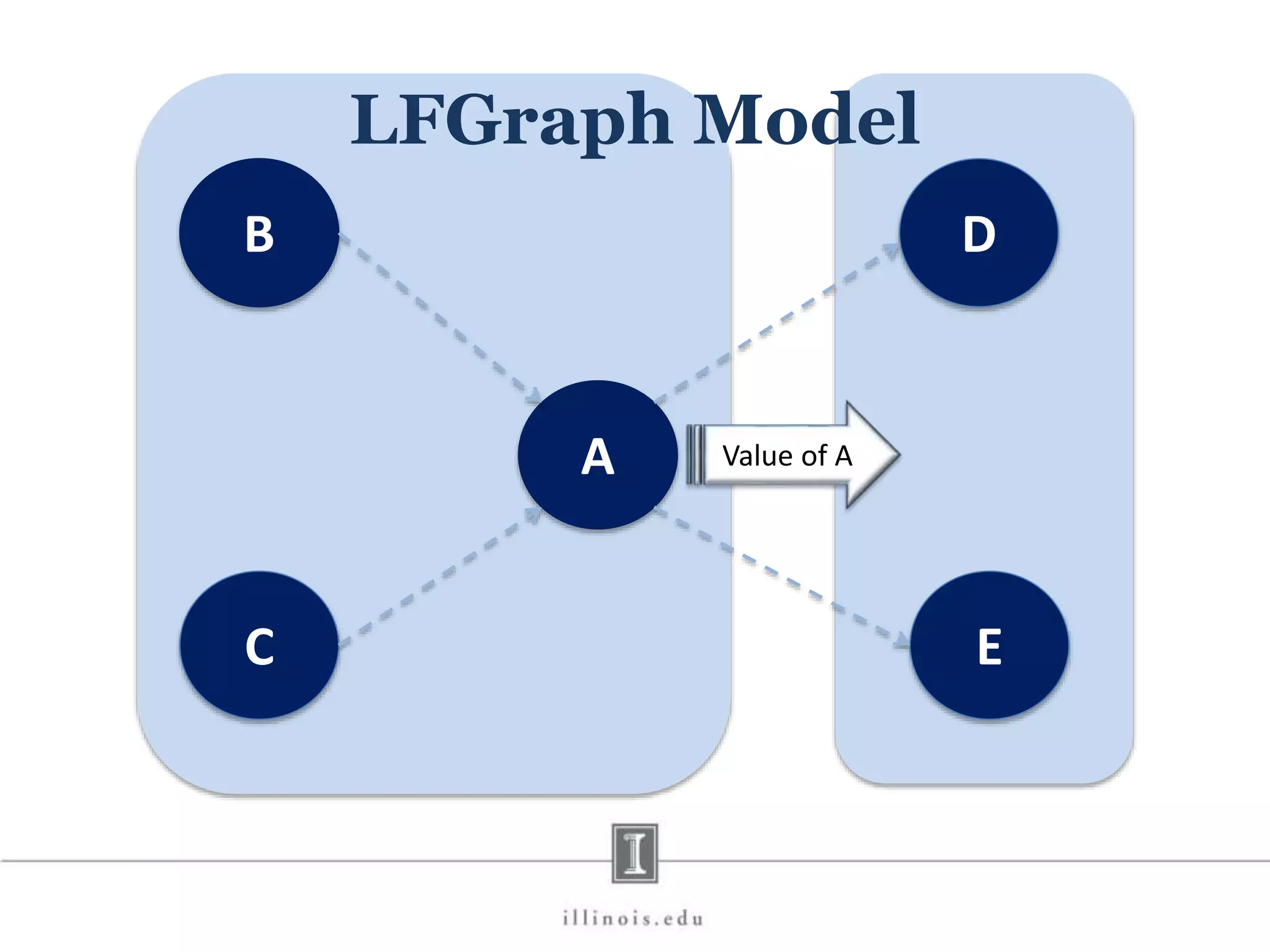
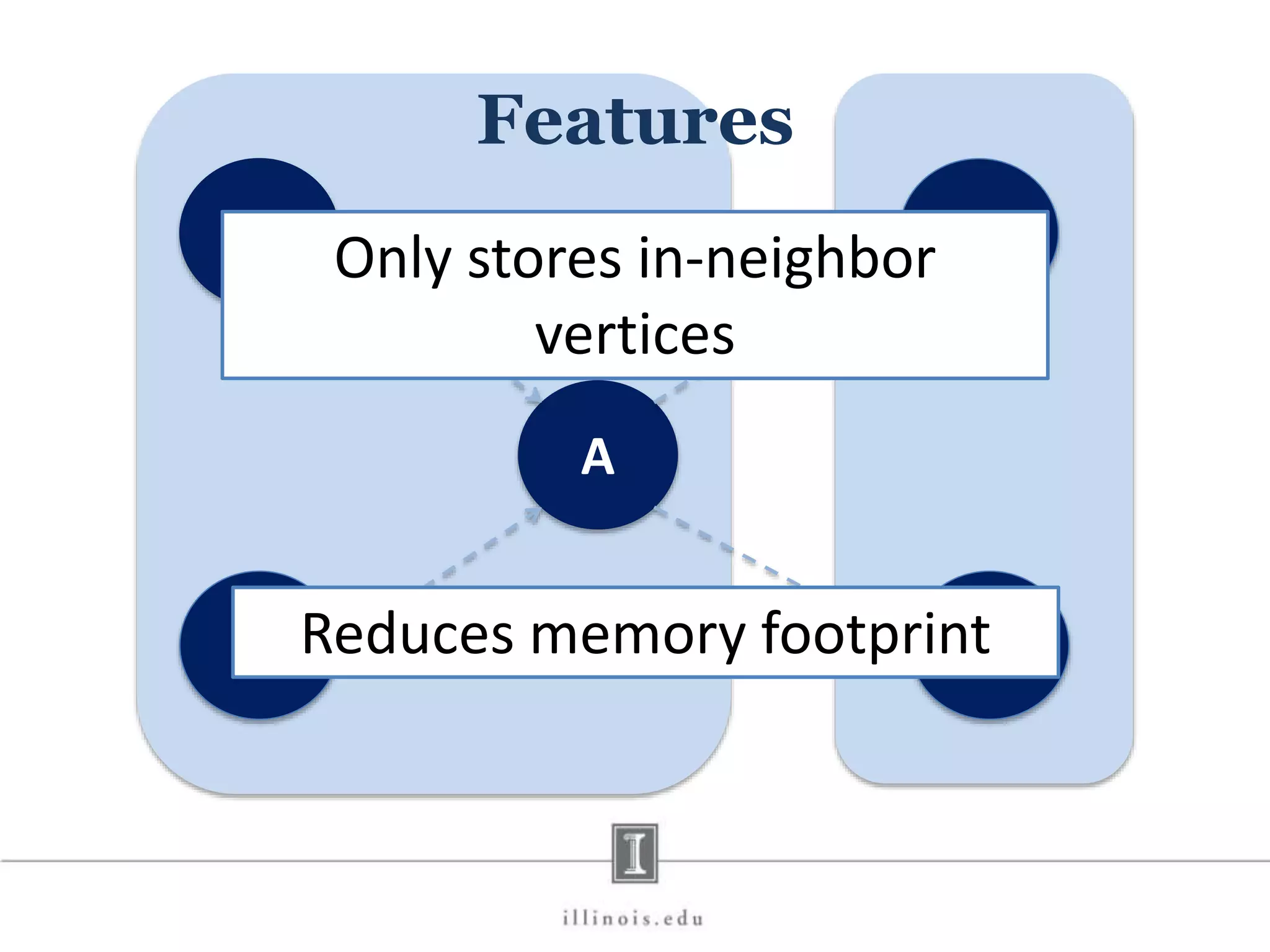
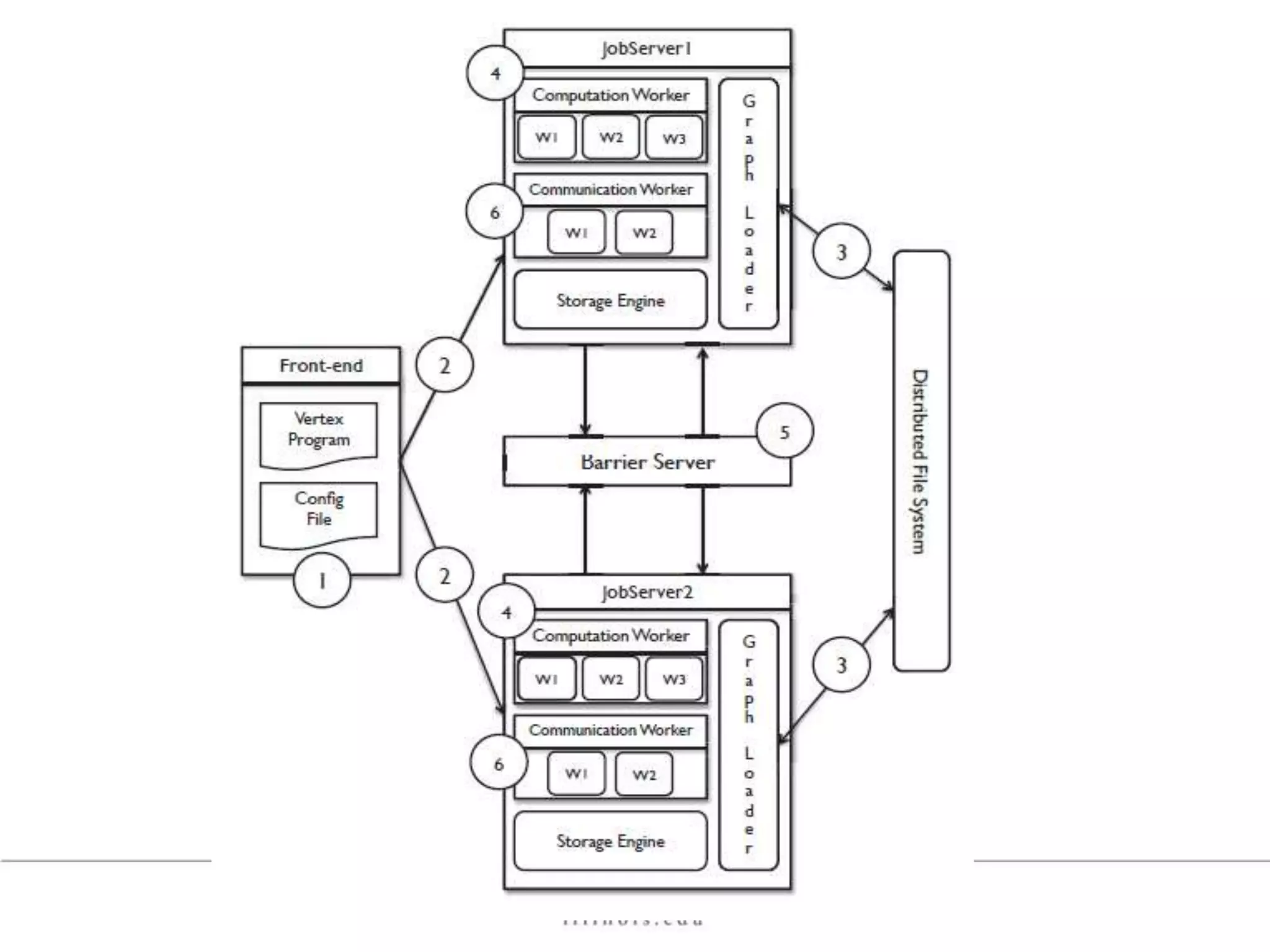
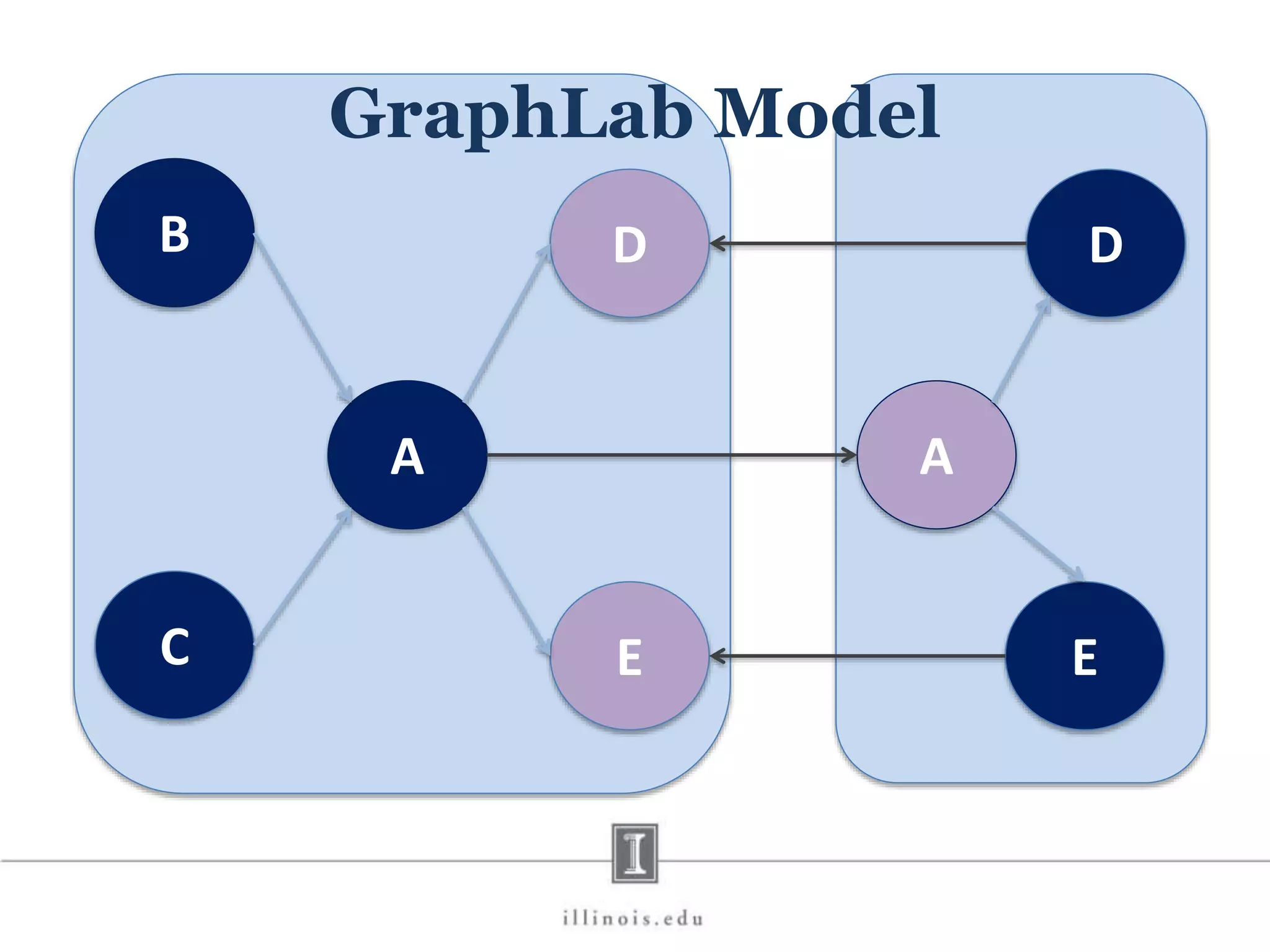
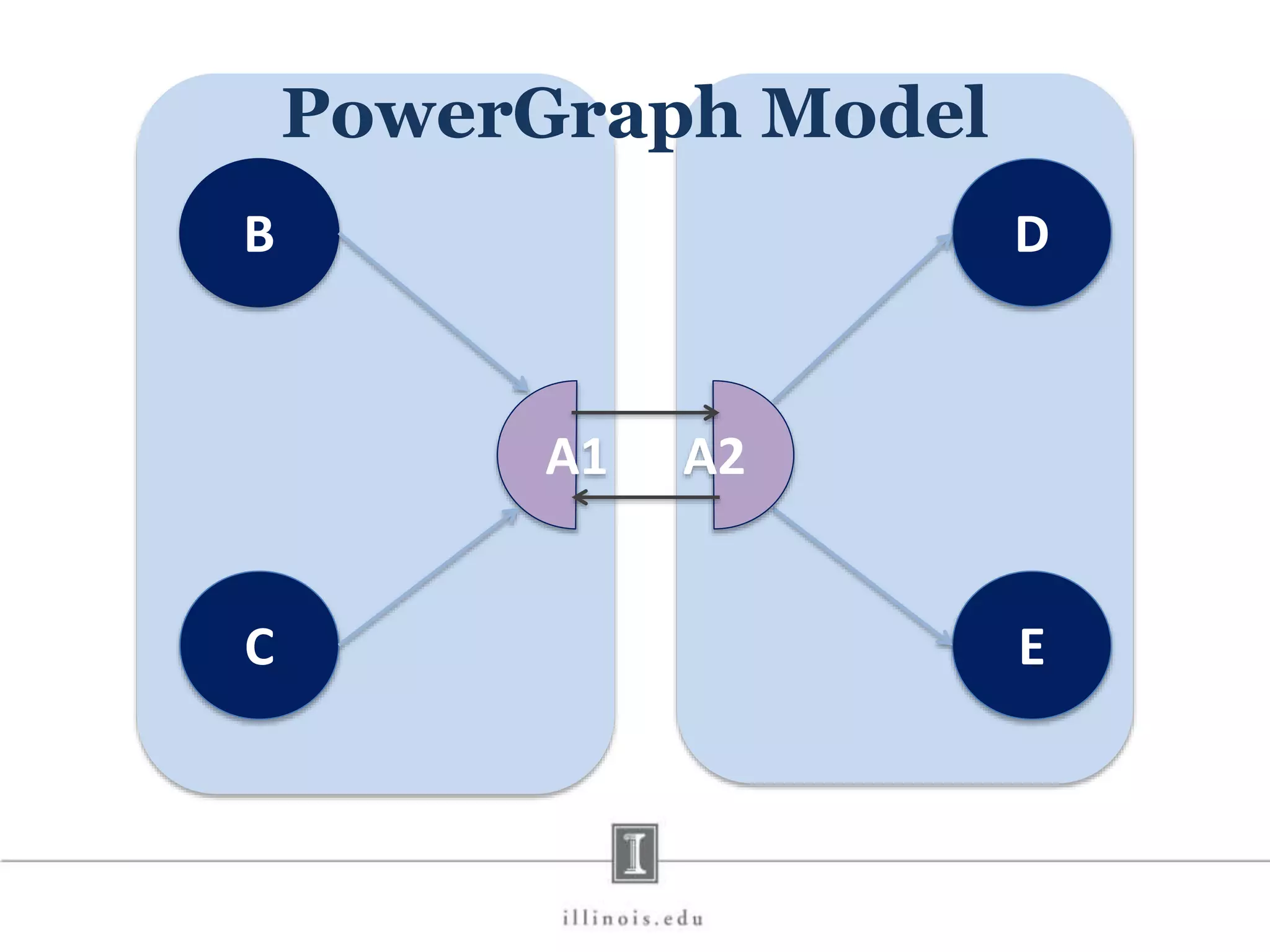
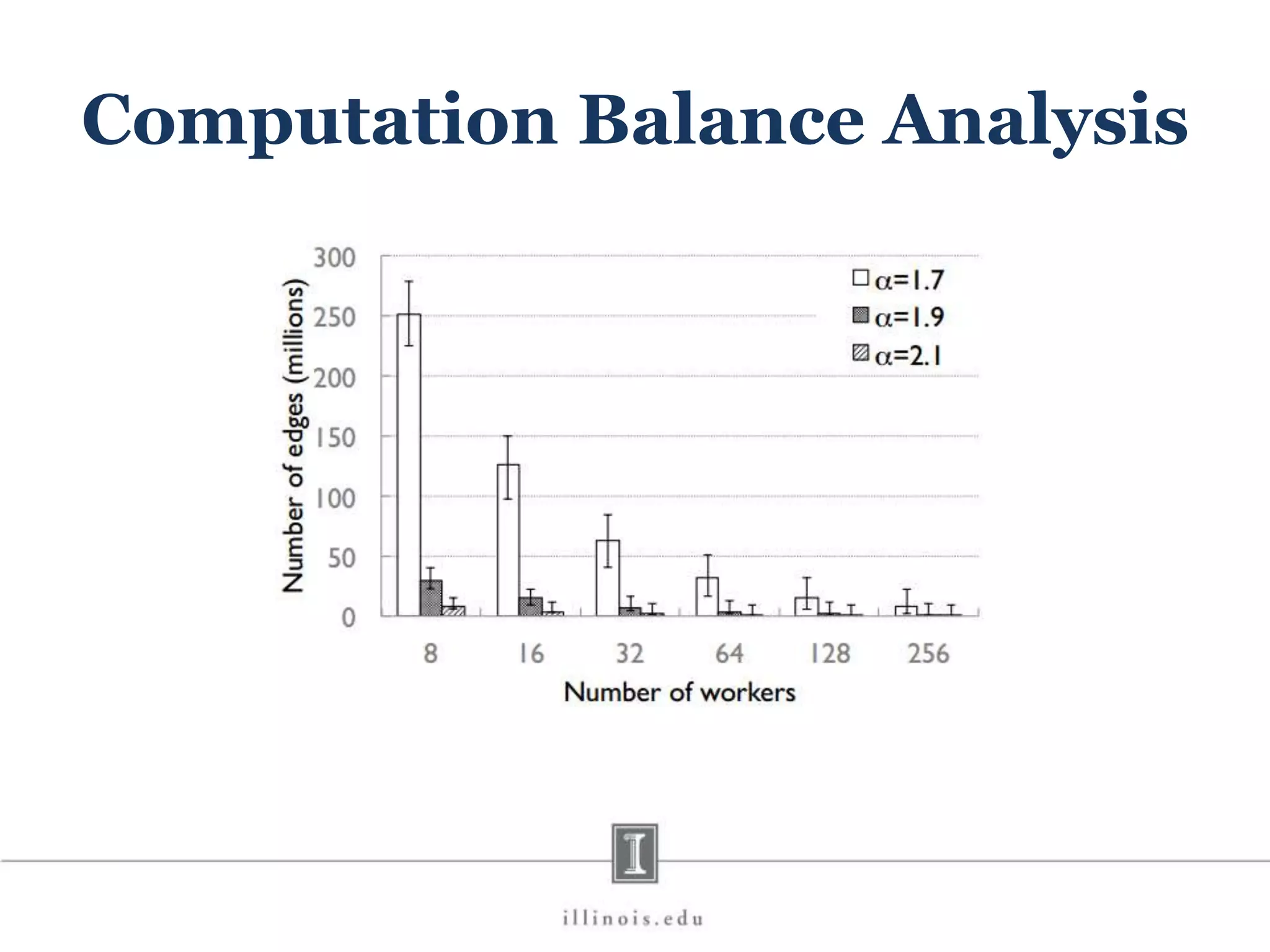
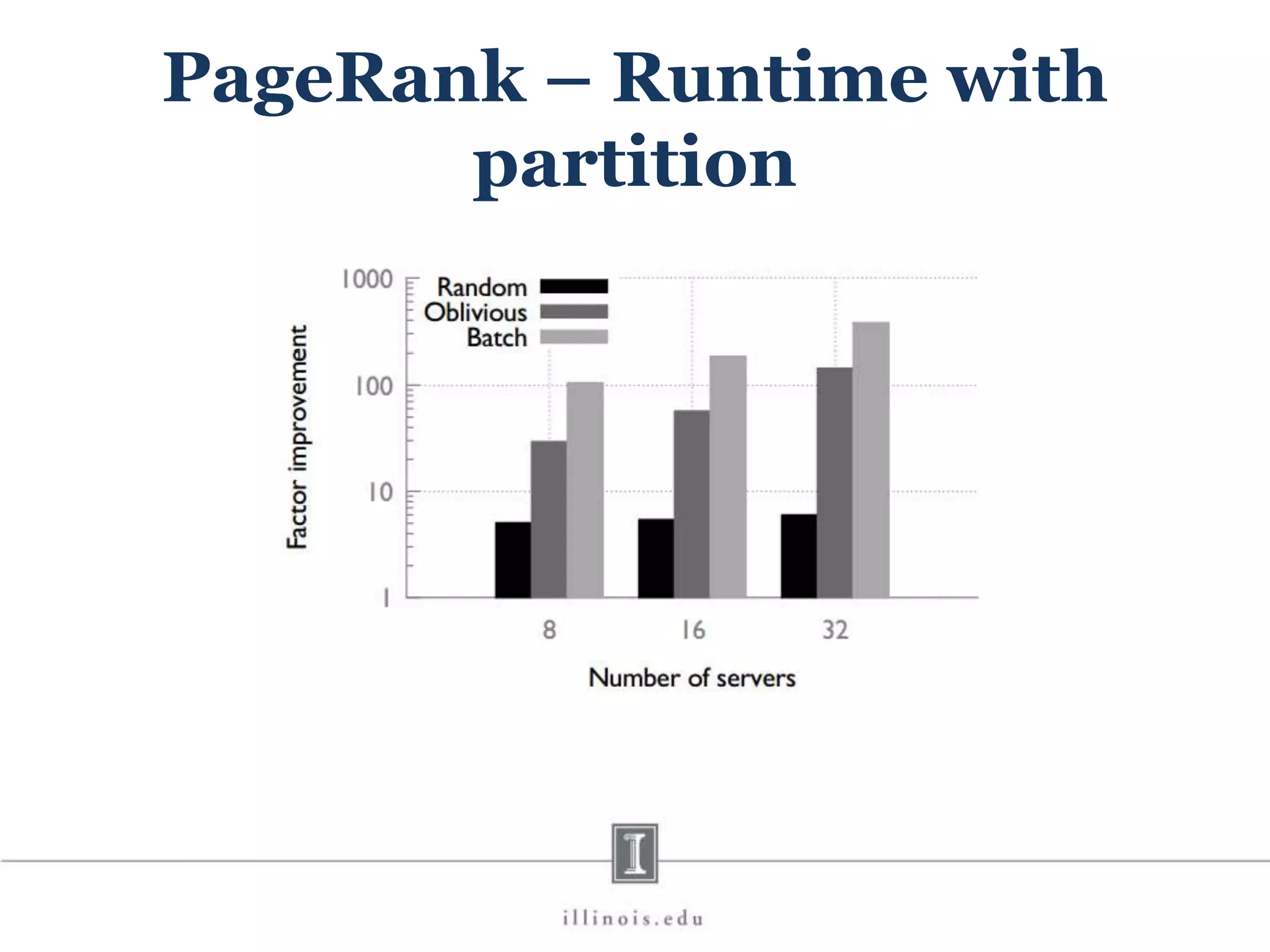
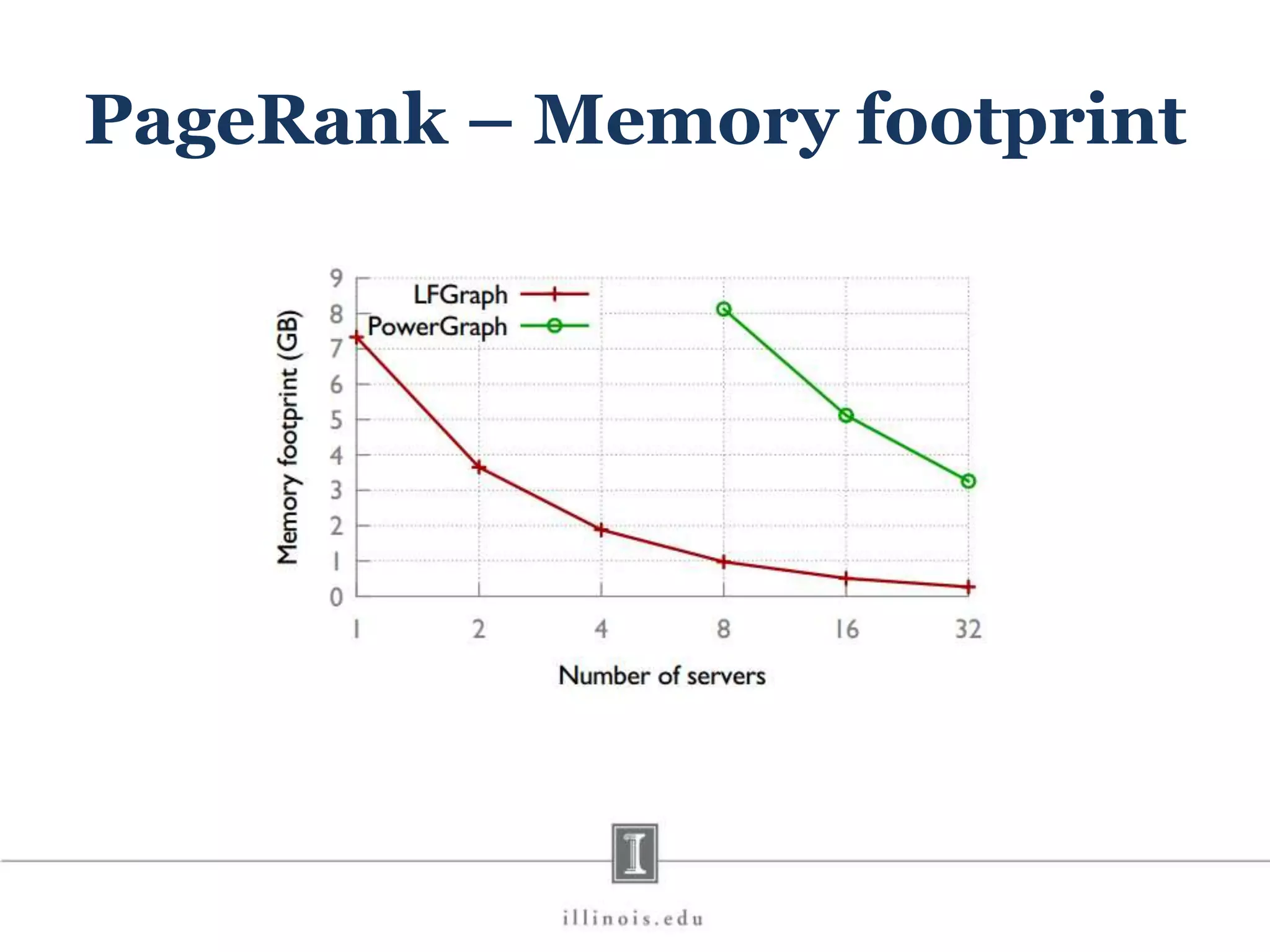
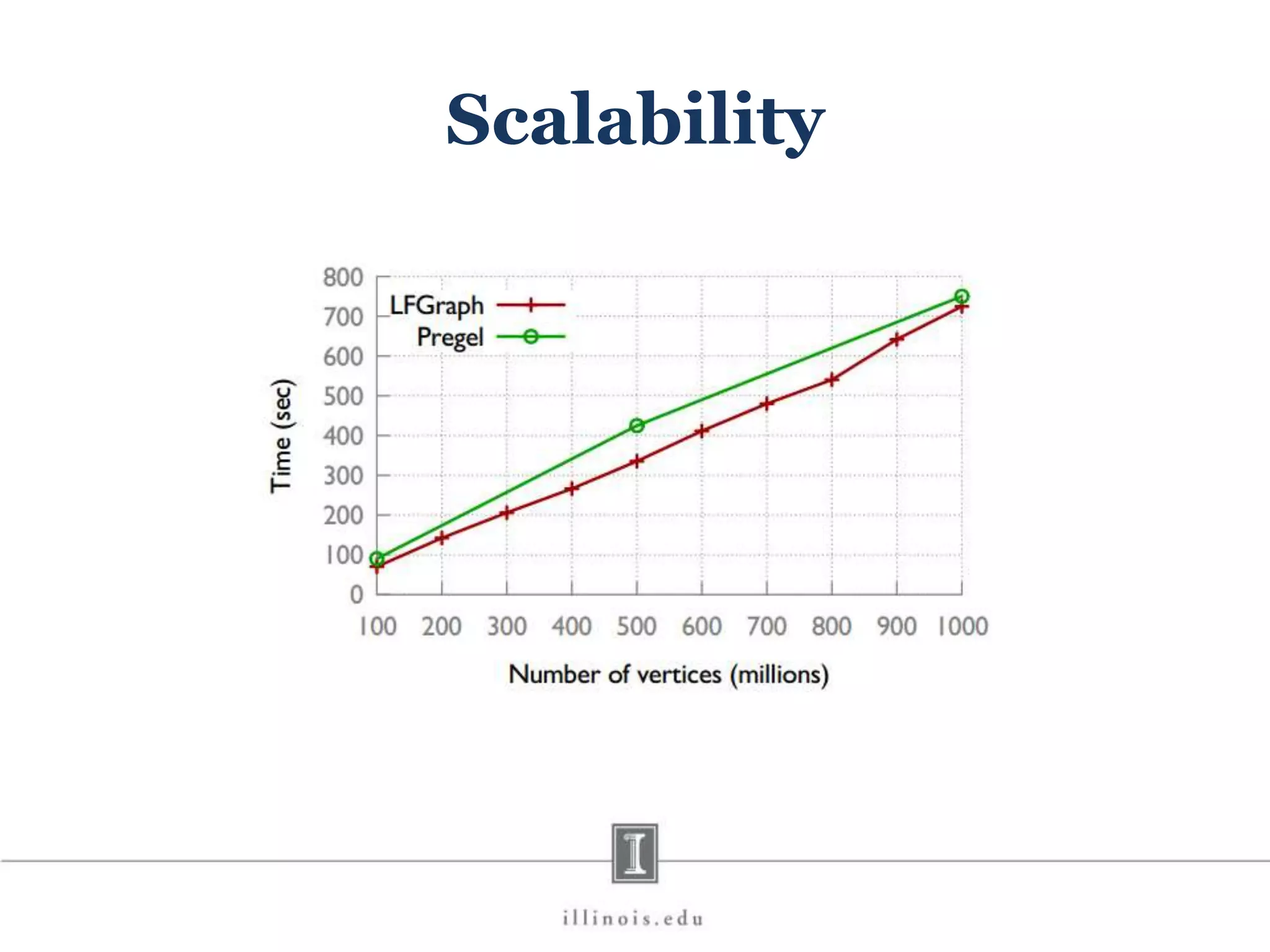
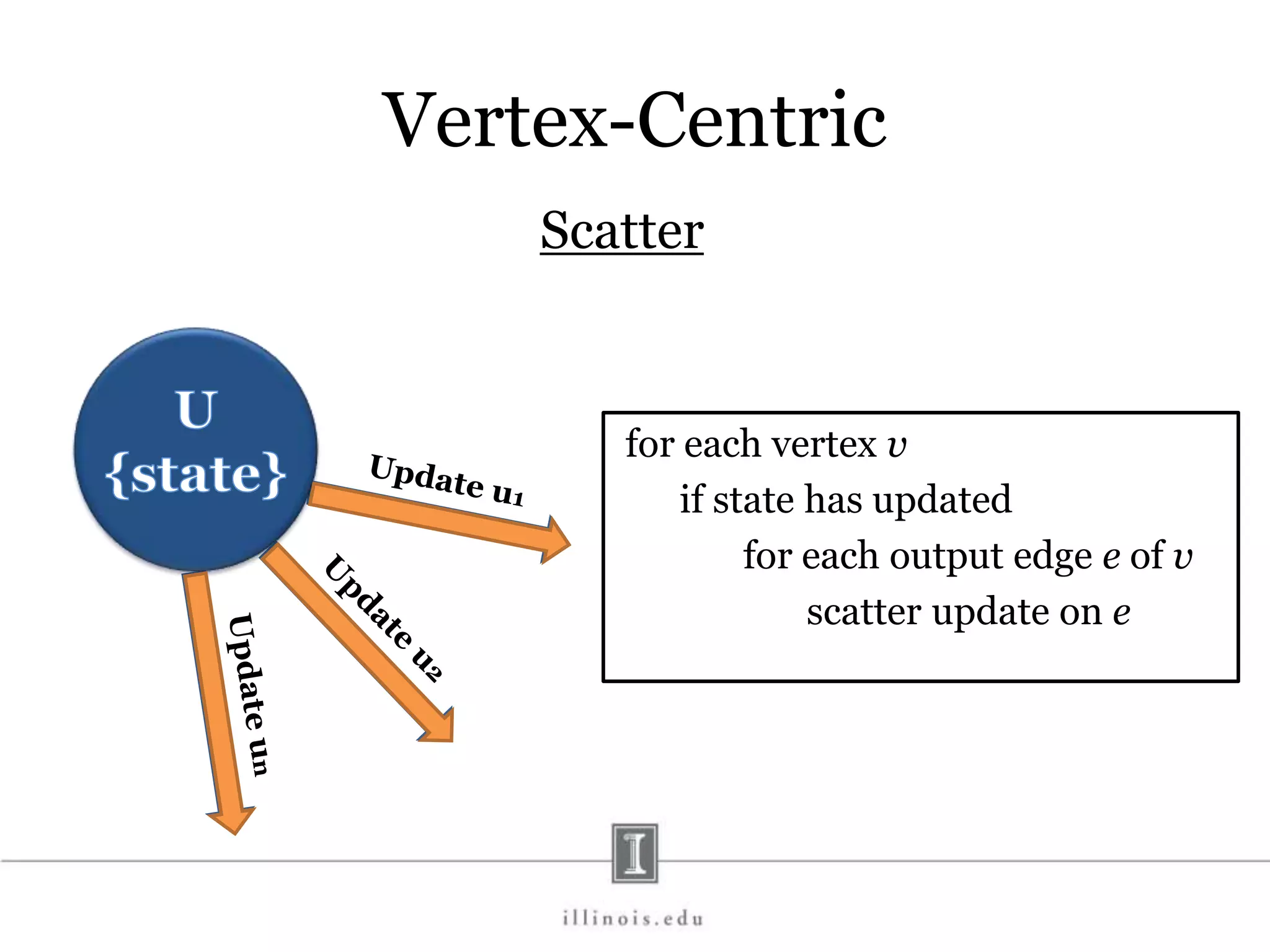
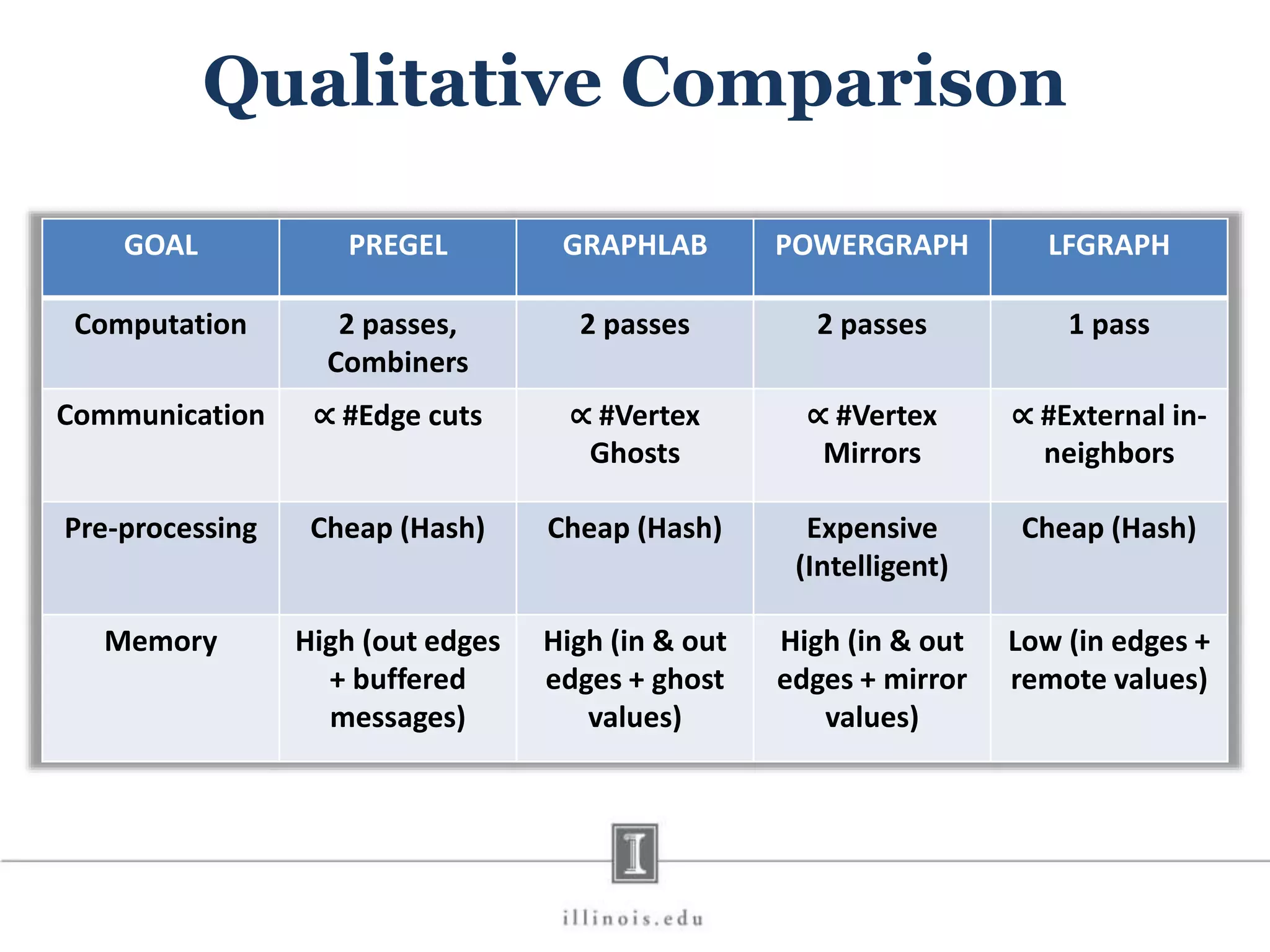
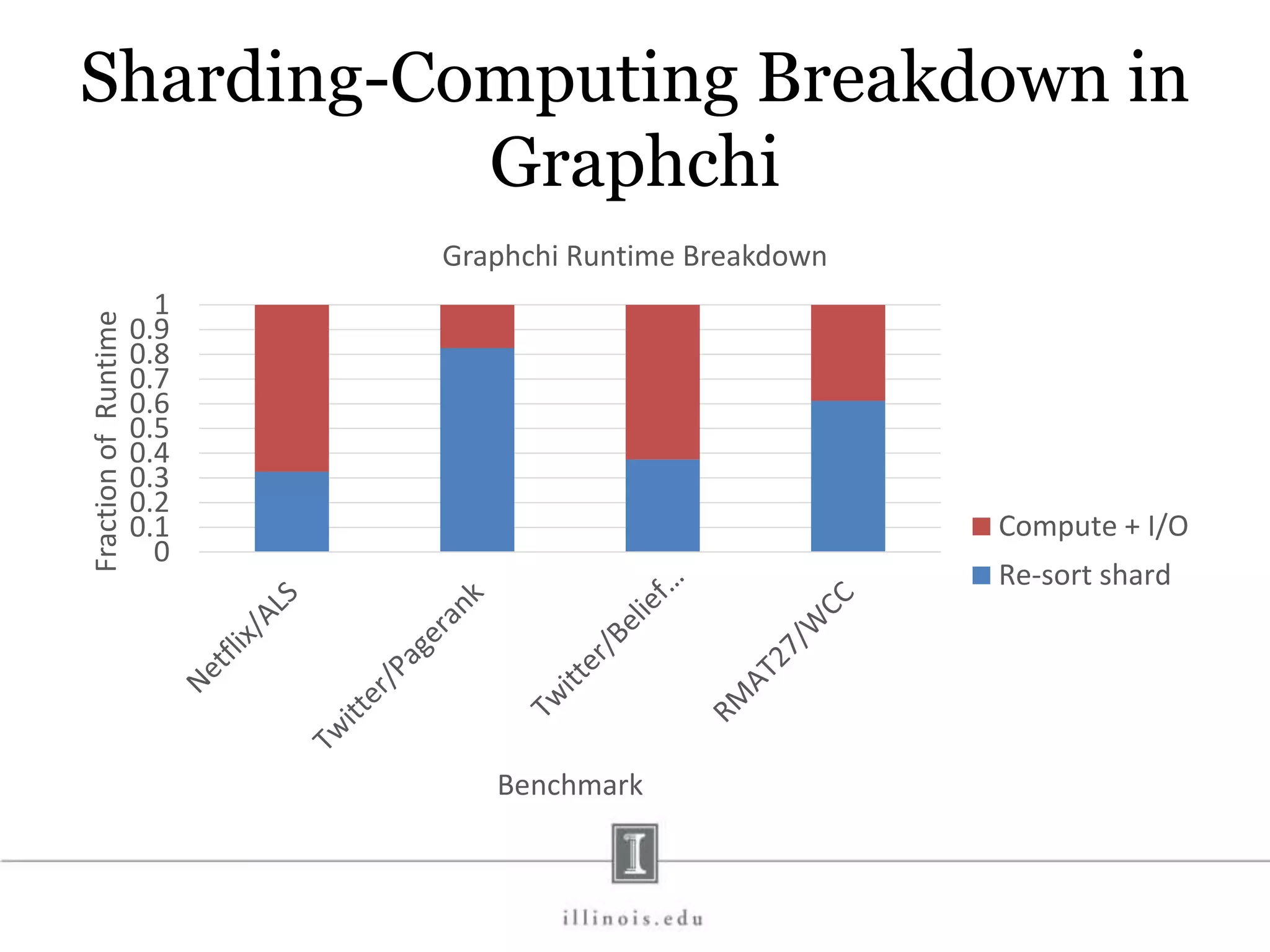
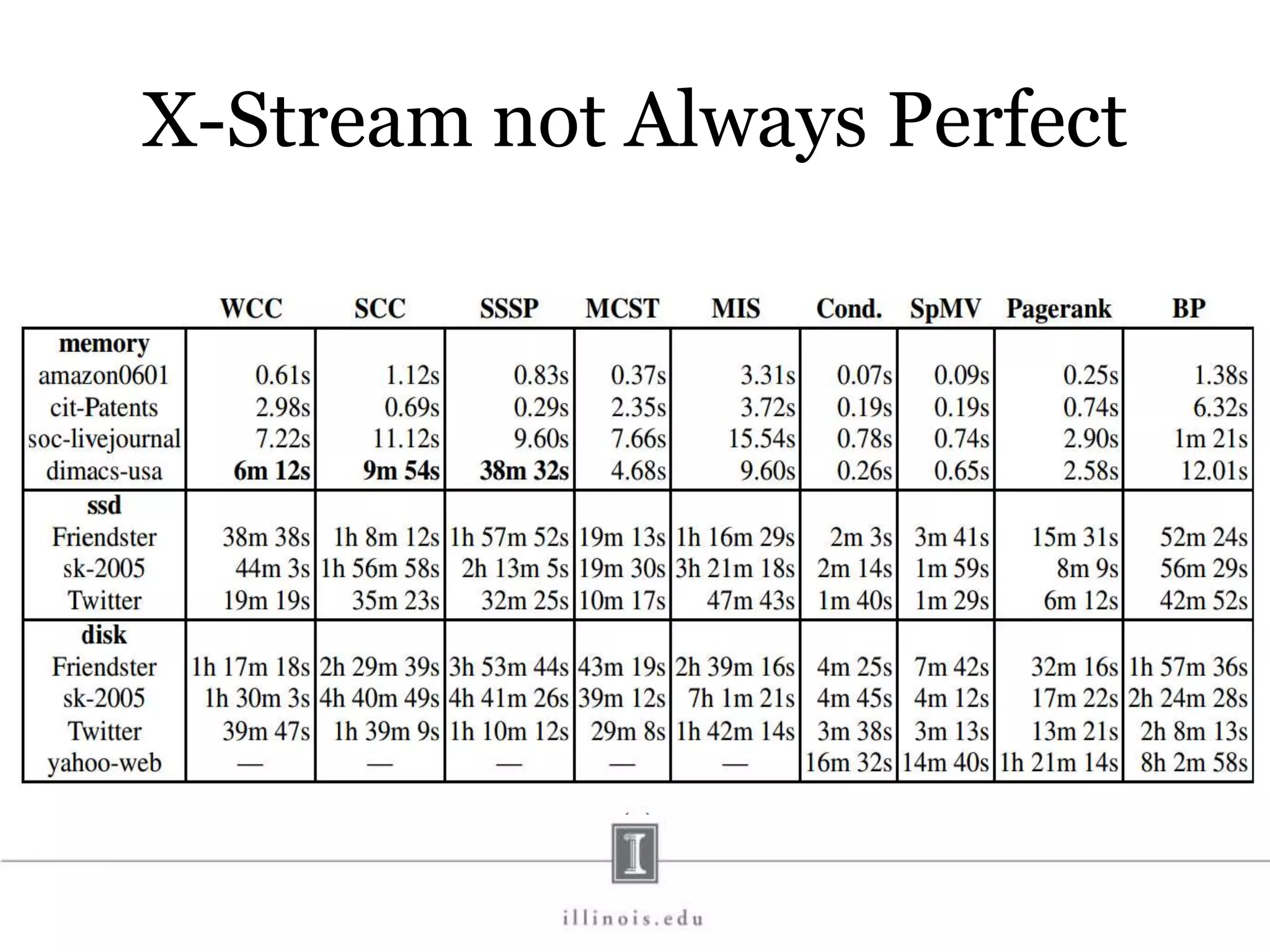
This document discusses graph processing and the need for distributed graph frameworks. It provides examples of real-world graph sizes that are too large for a single machine to process. It then summarizes some of the key challenges in parallel graph processing like irregular structure and data transfer issues. Several graph processing frameworks are described including Pregel, GraphLab, PowerGraph, and LFGraph. LFGraph is presented as a simple and fast distributed graph analytics framework that aims to have low pre-processing, load-balanced computation and communication, and low memory footprint compared to previous frameworks. The document provides examples and analyses to compare the computation and communication characteristics of different frameworks. It concludes by discussing some open questions and potential areas for improvement in LFGraph.













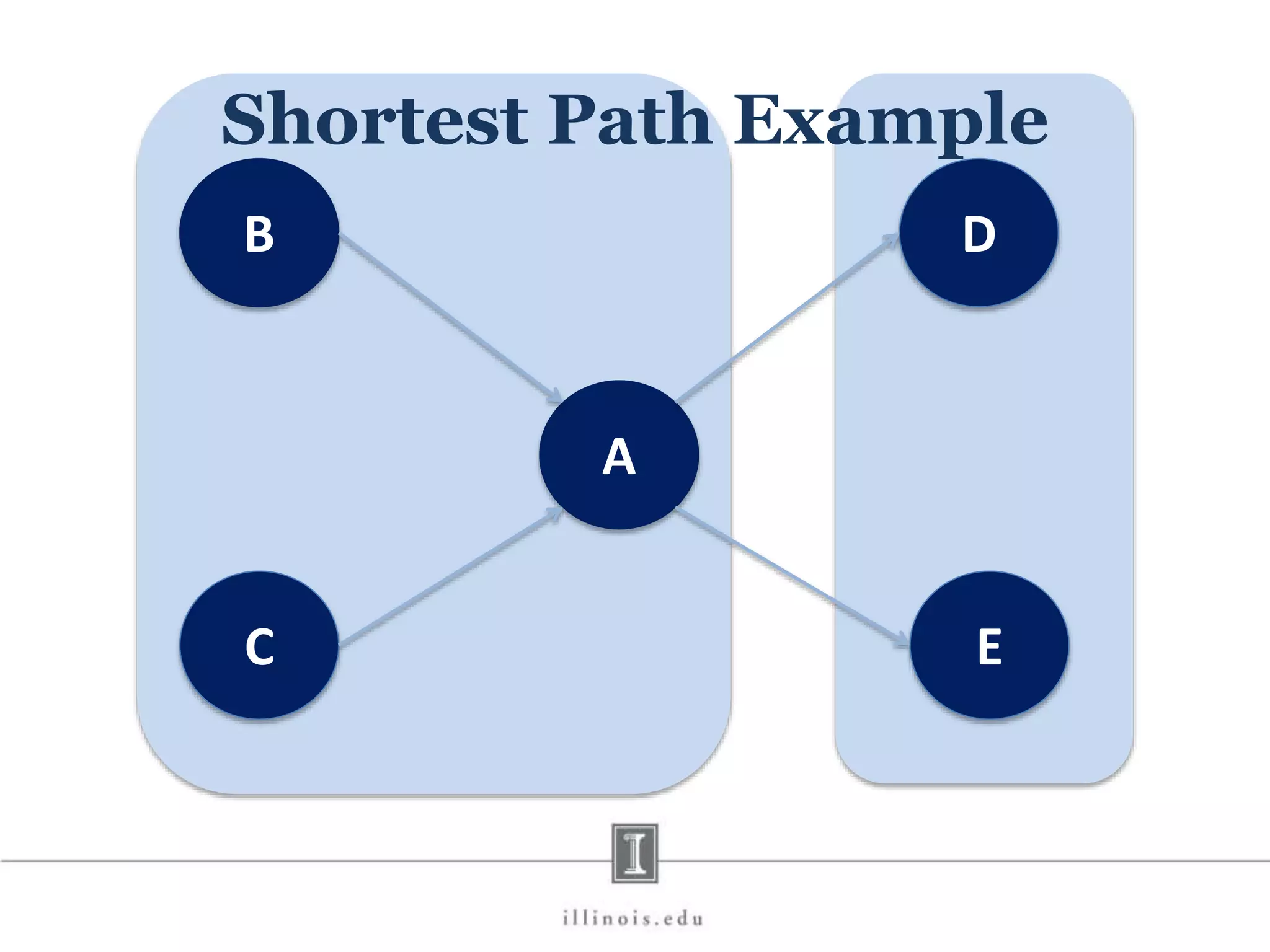

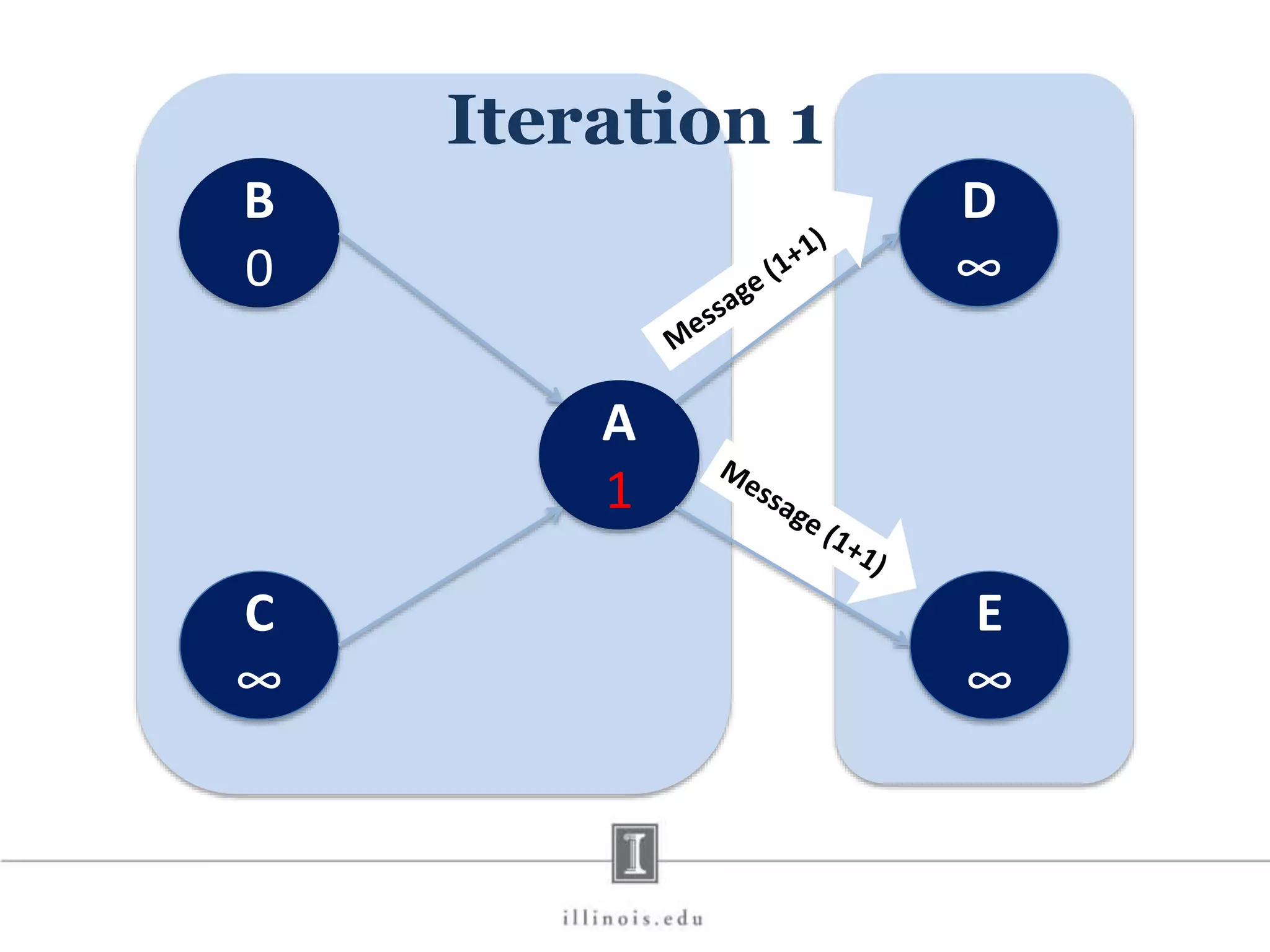
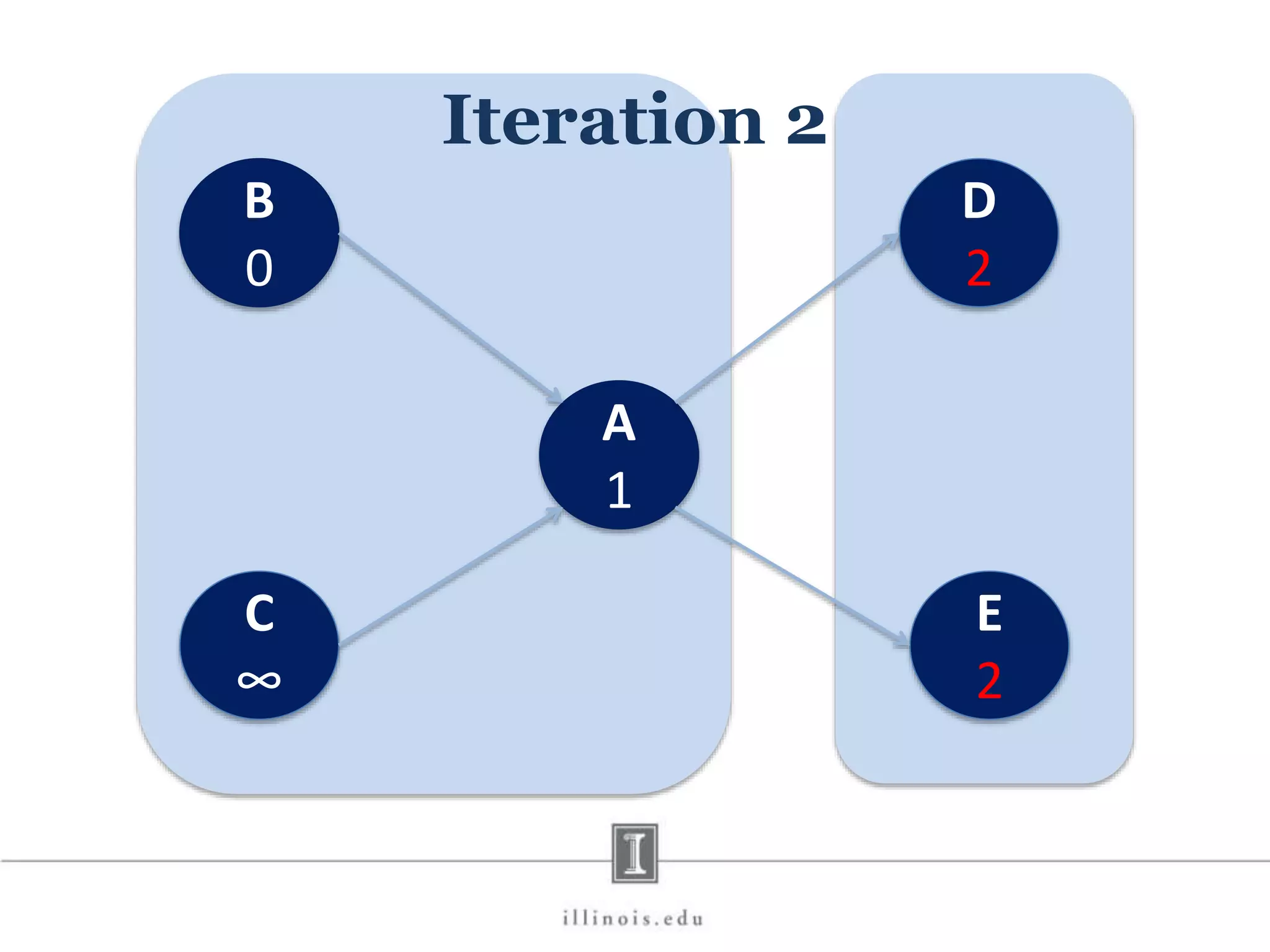


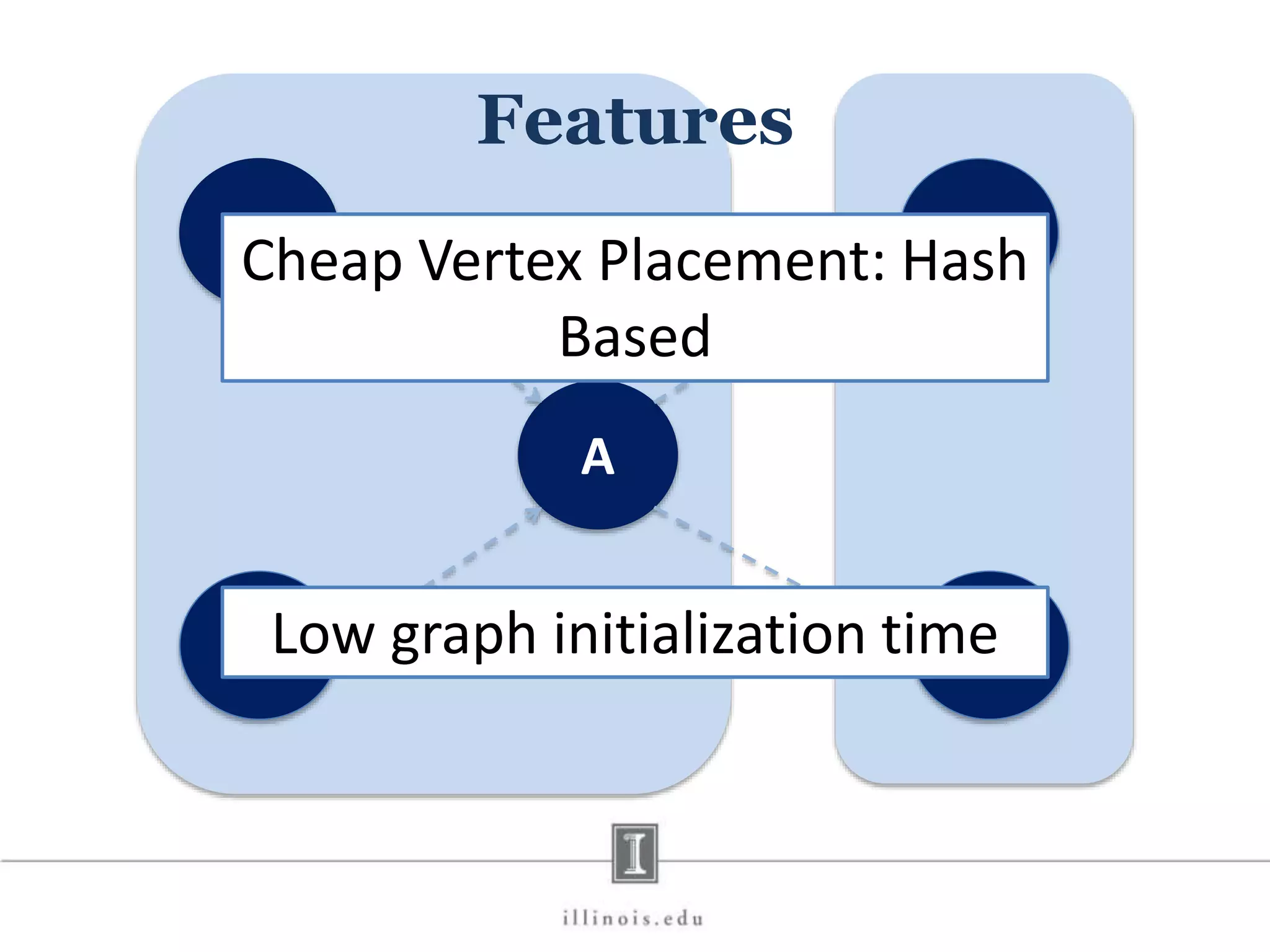

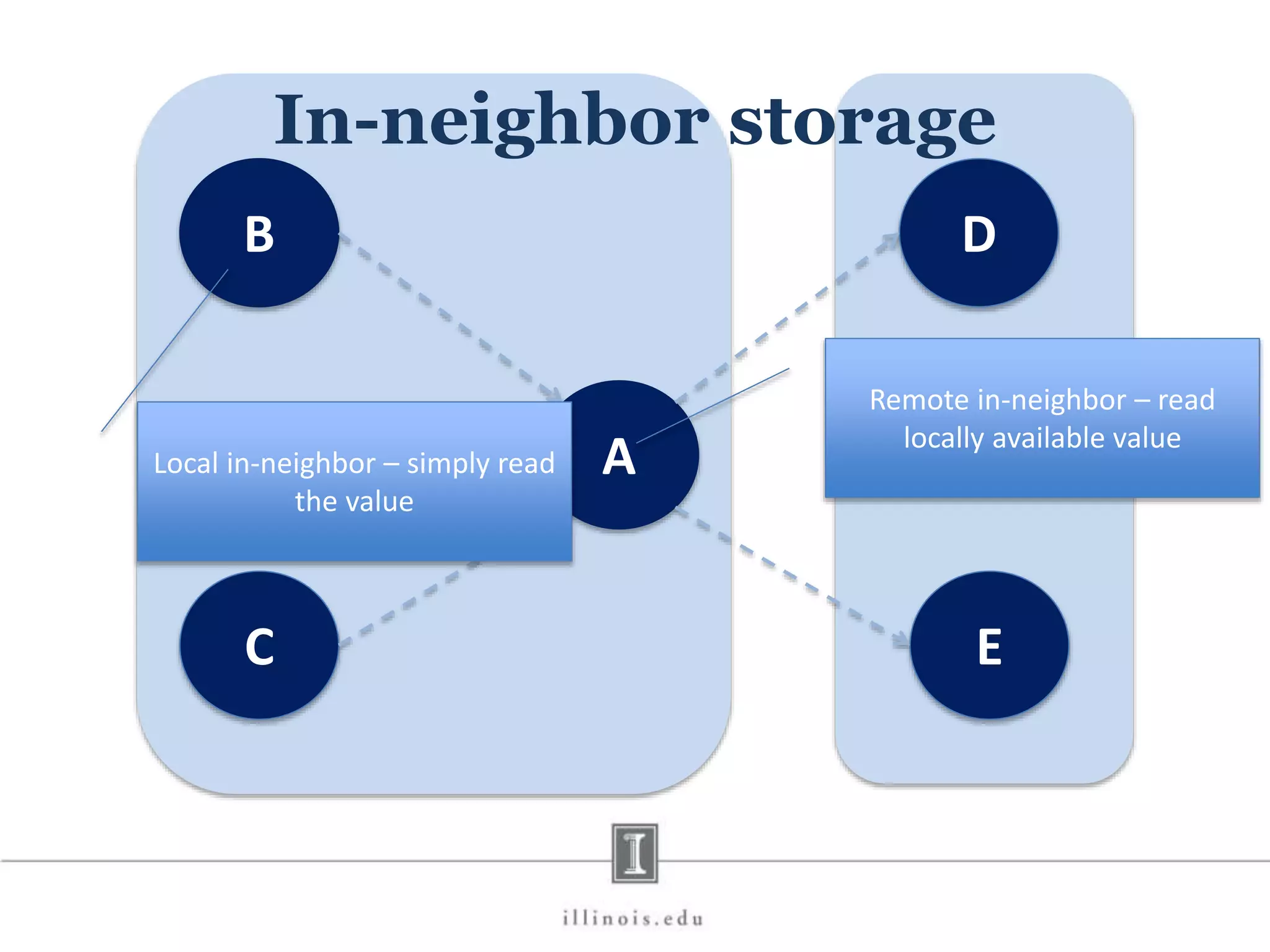

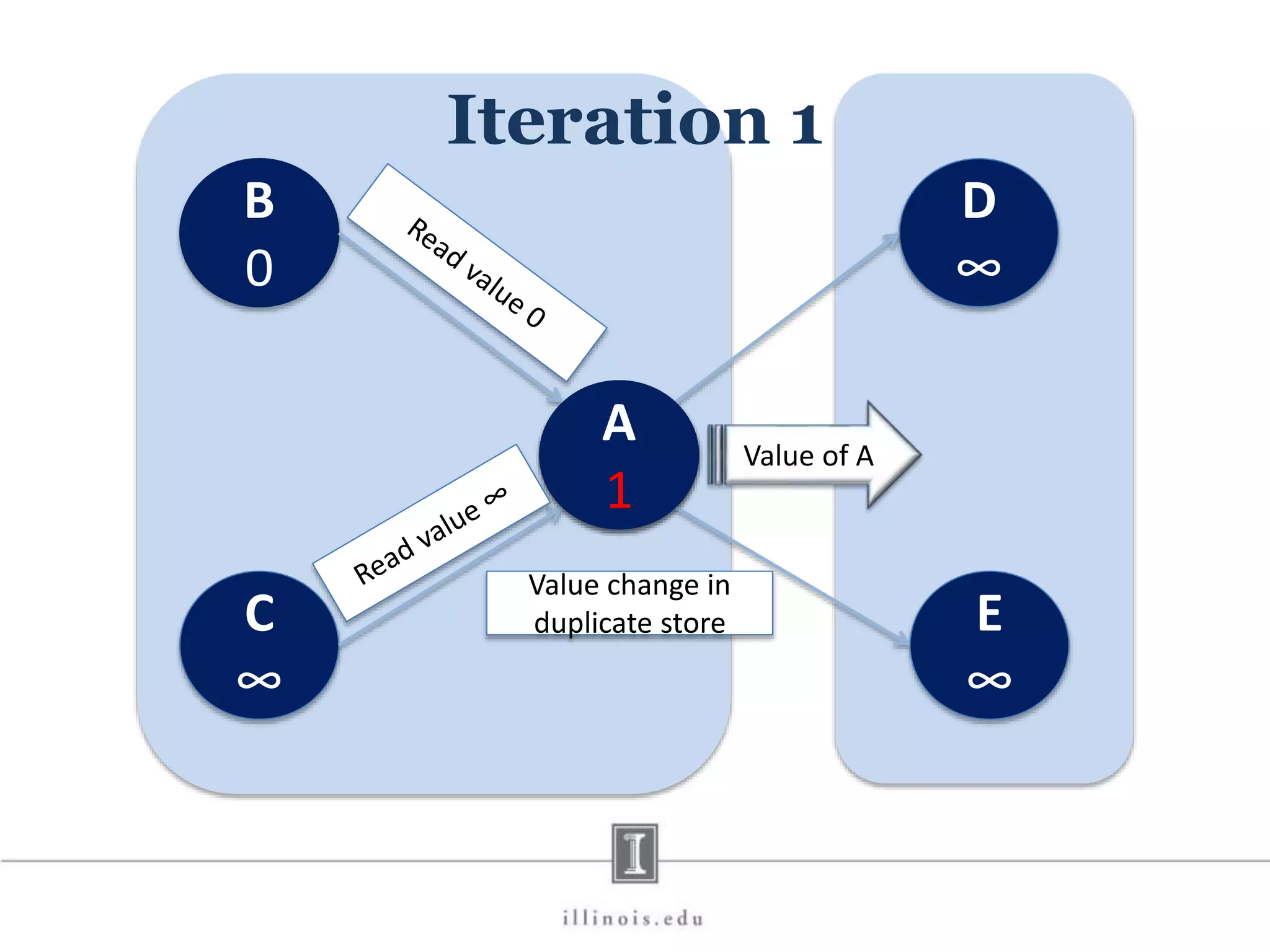
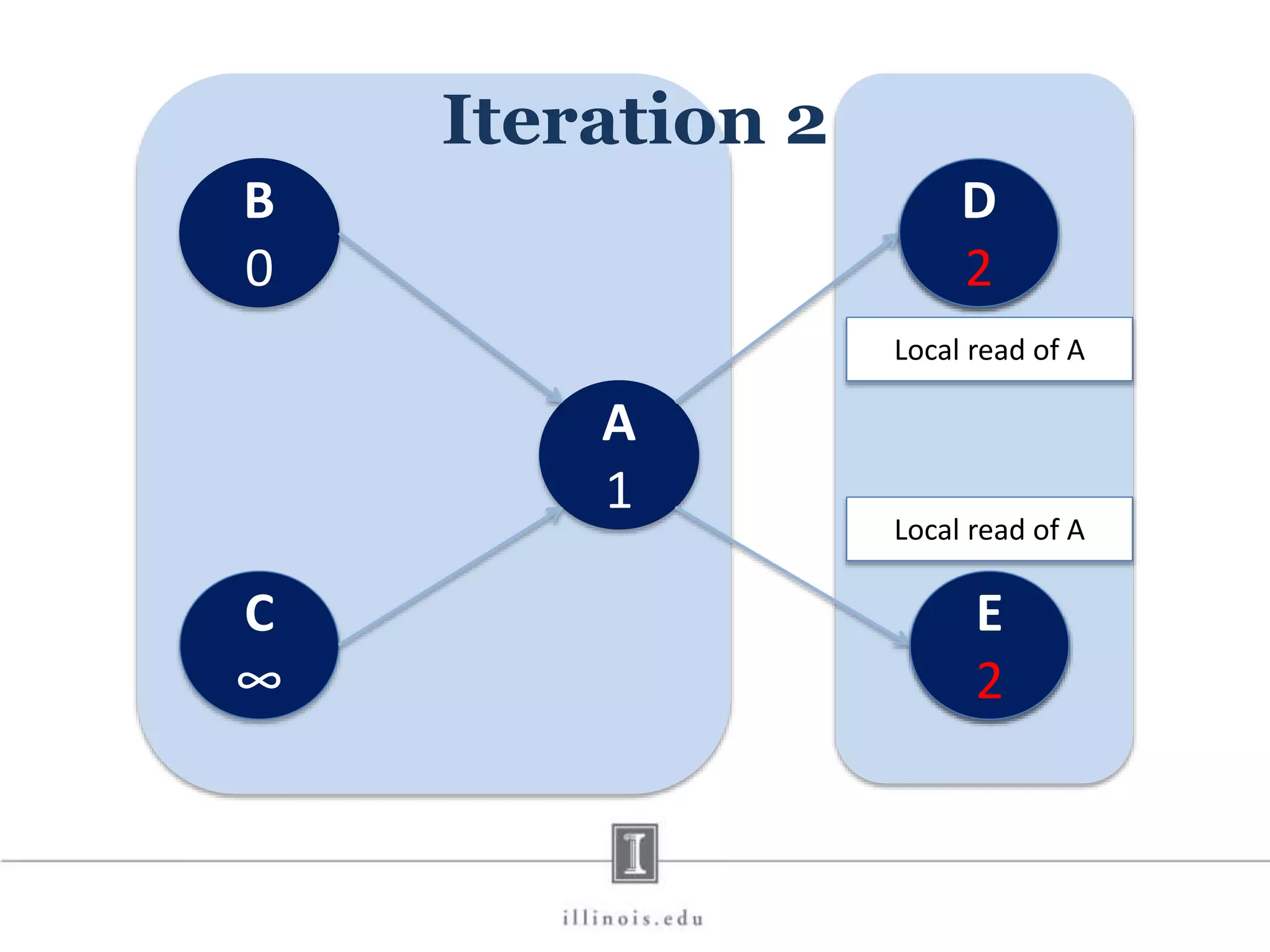








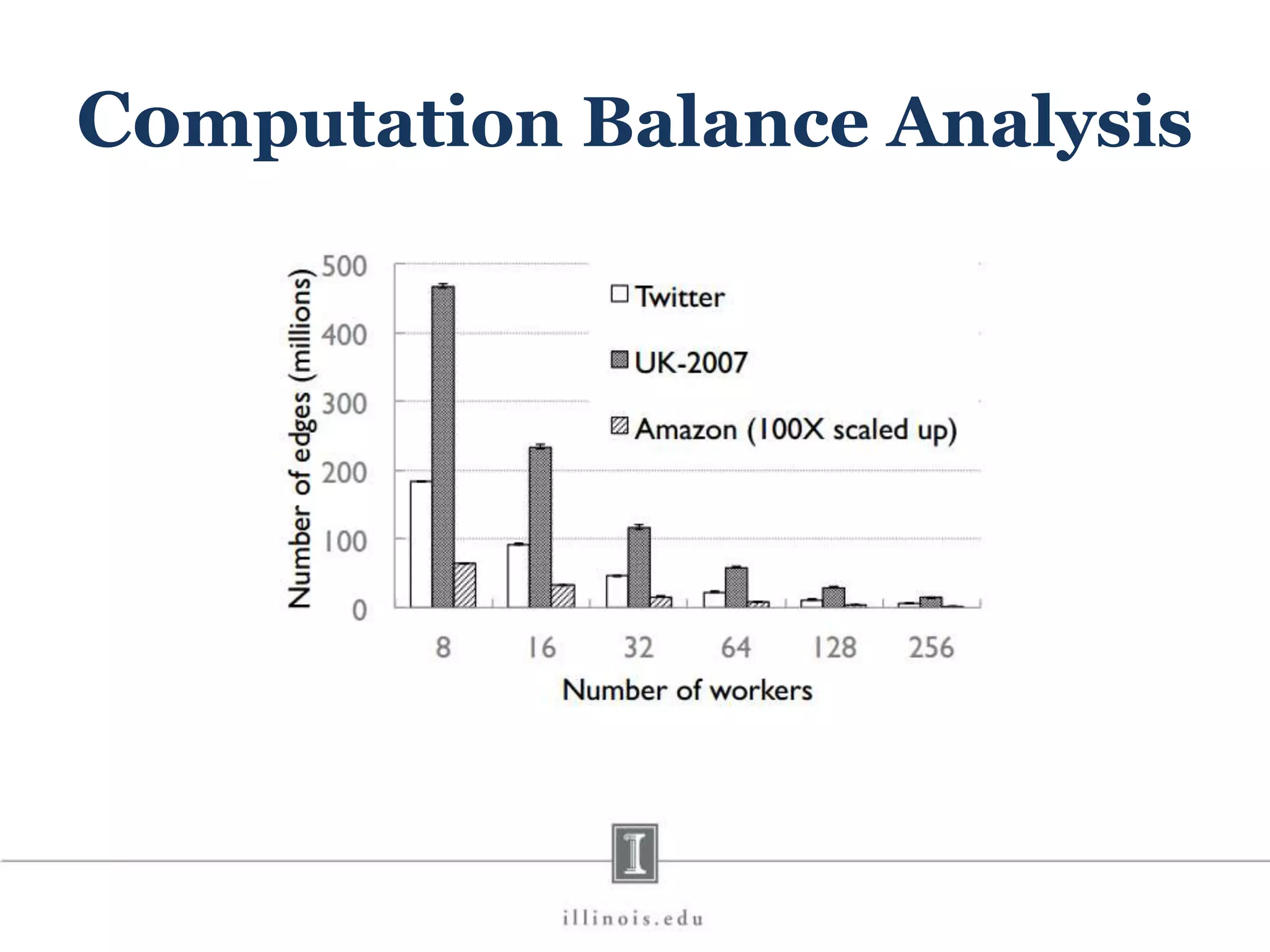
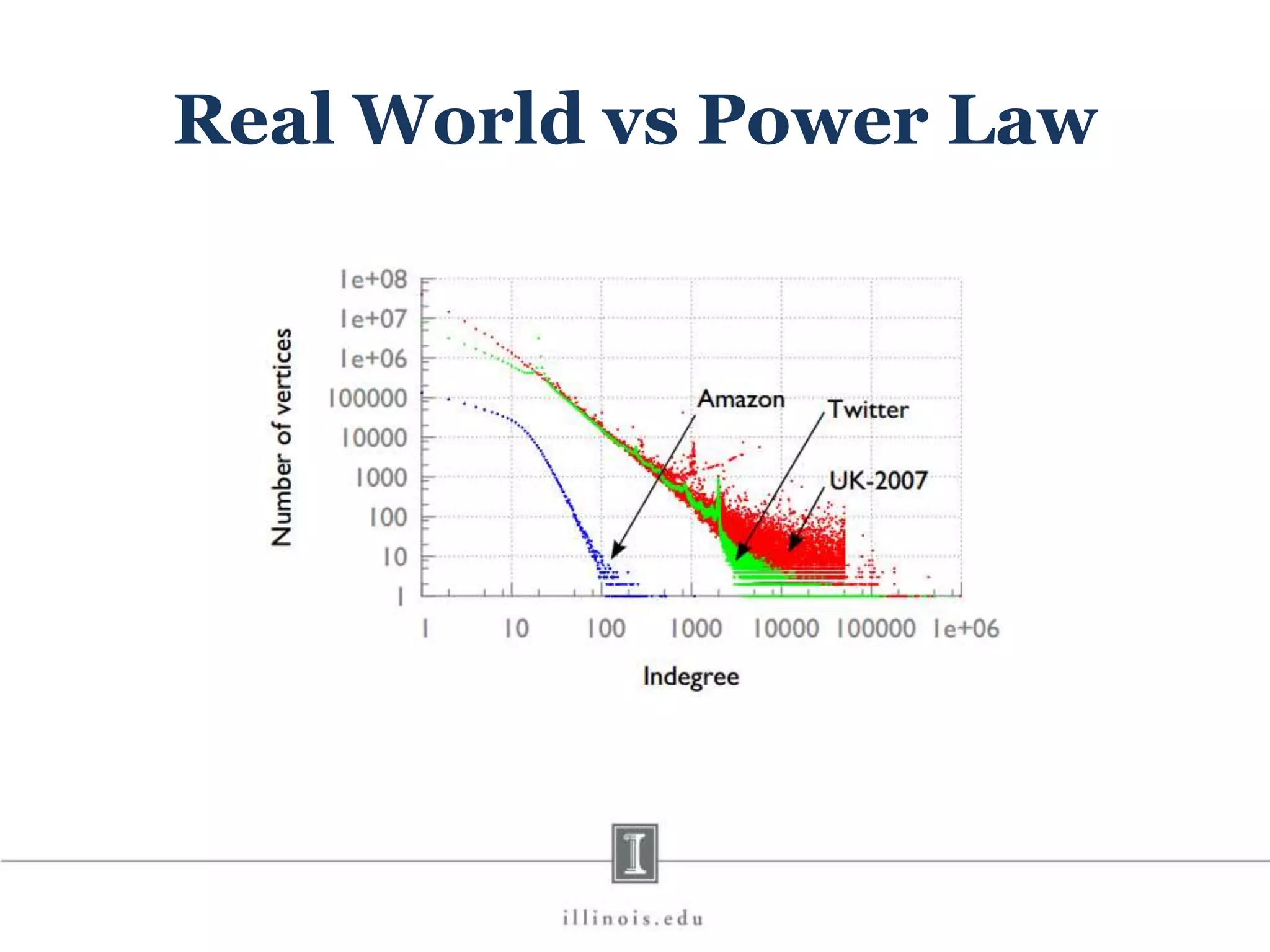
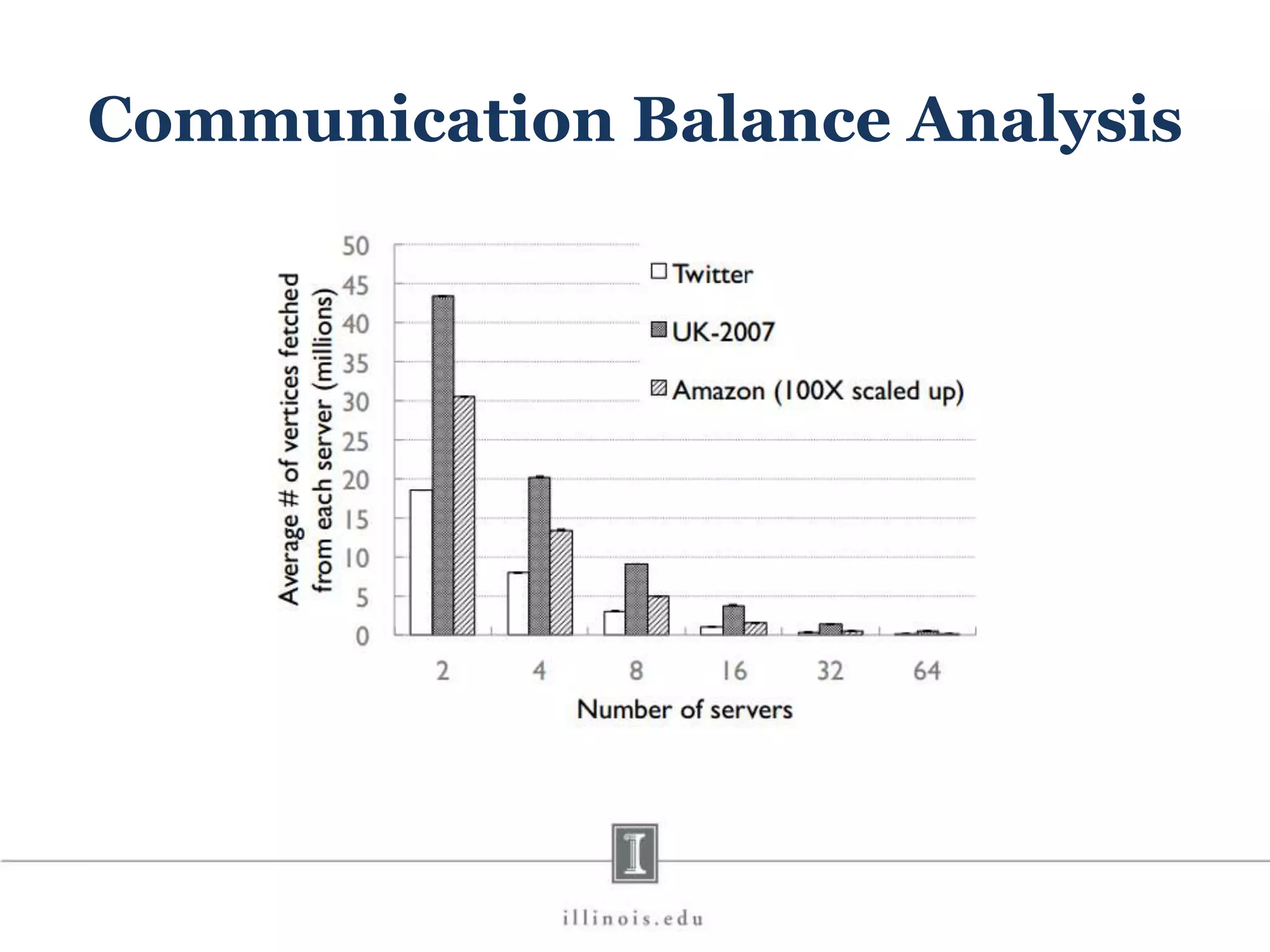
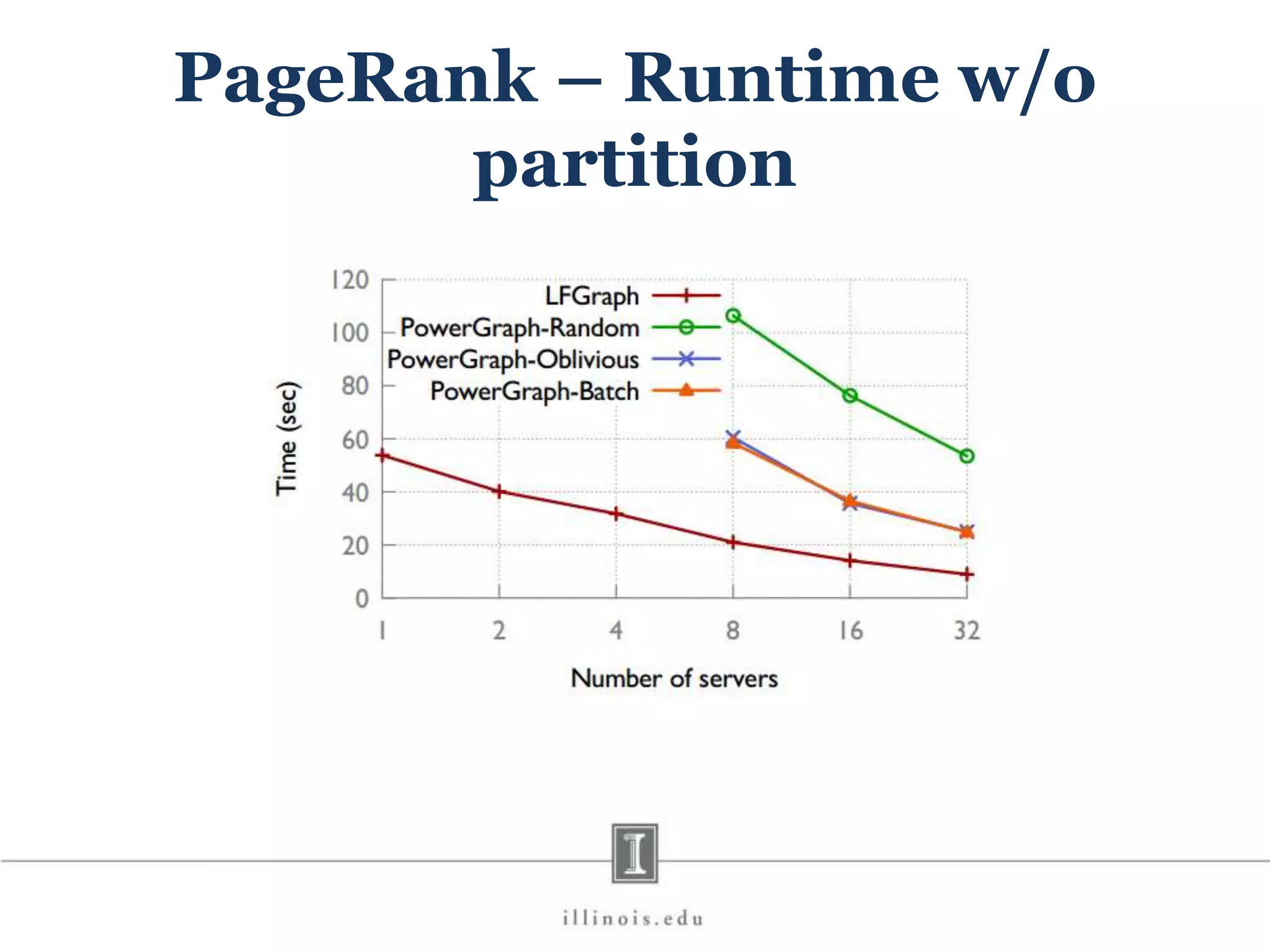










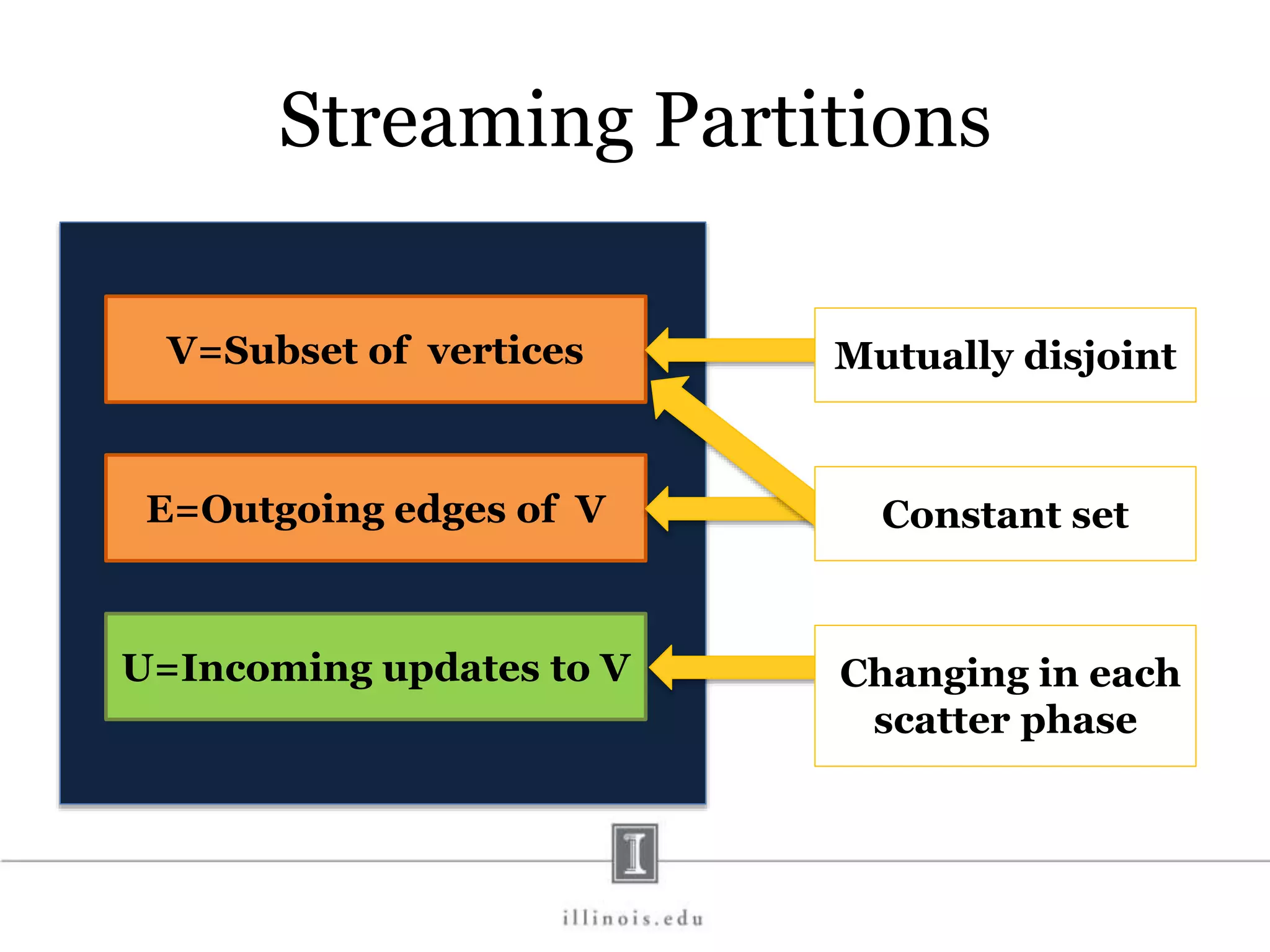

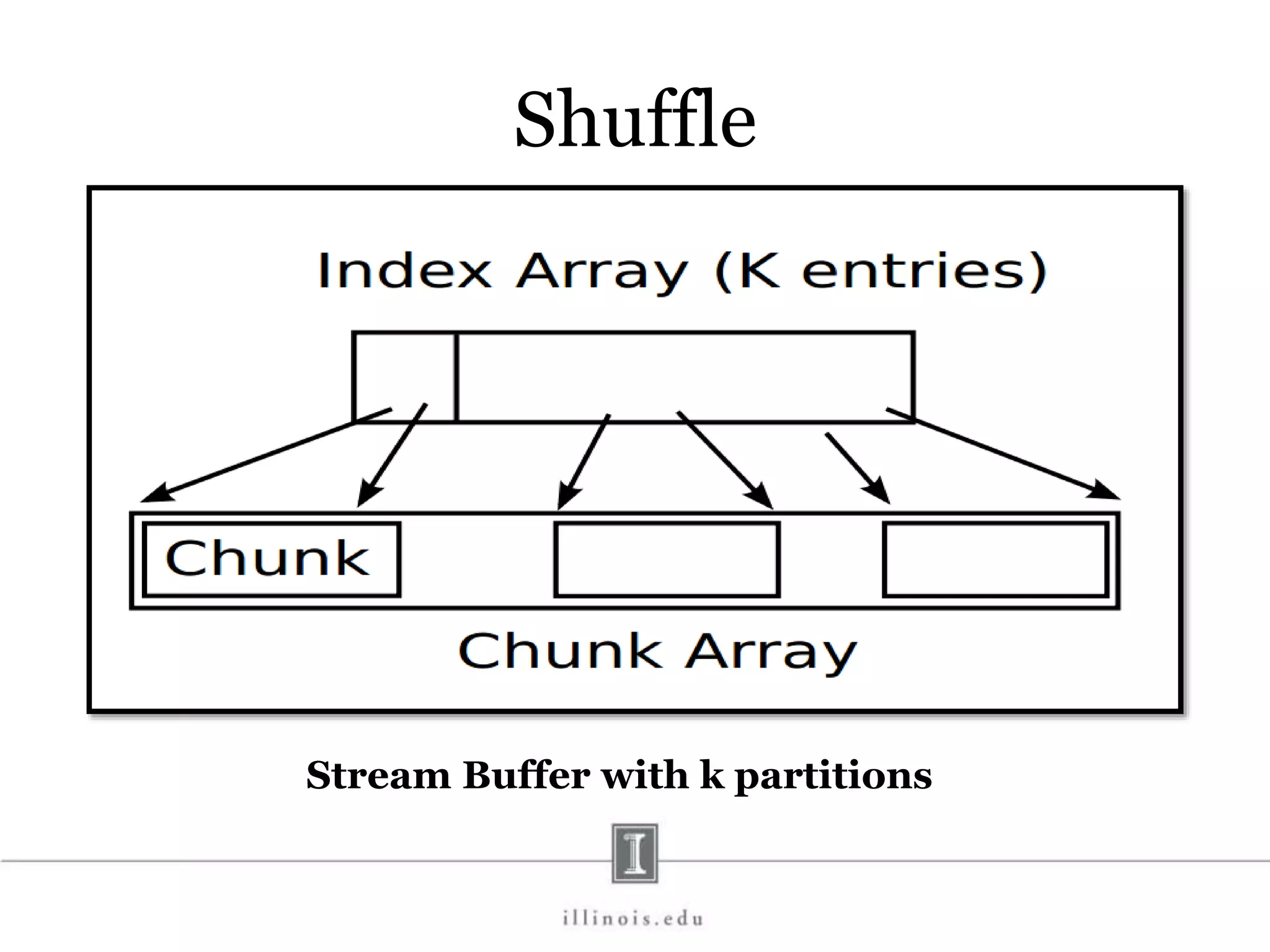
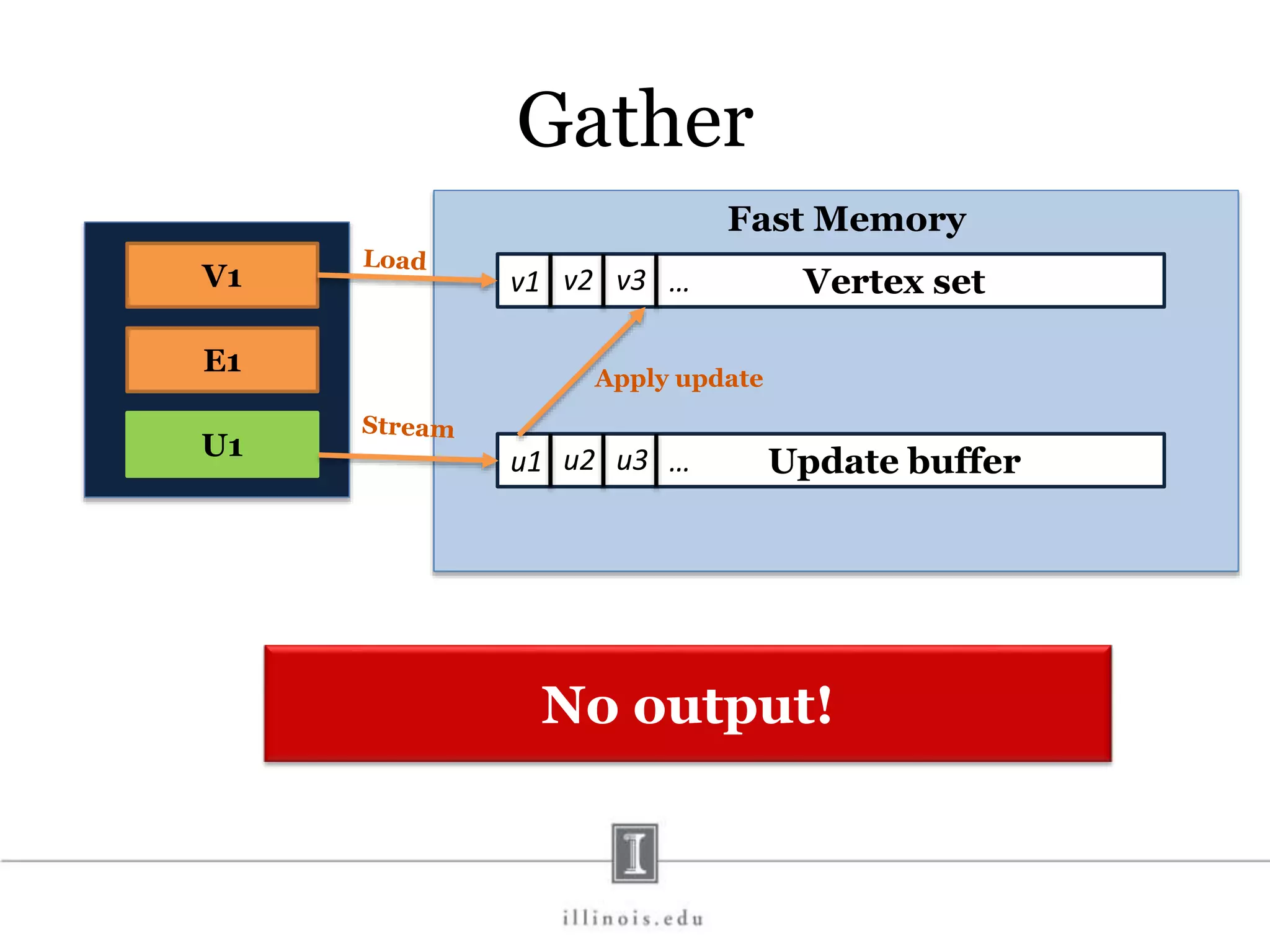


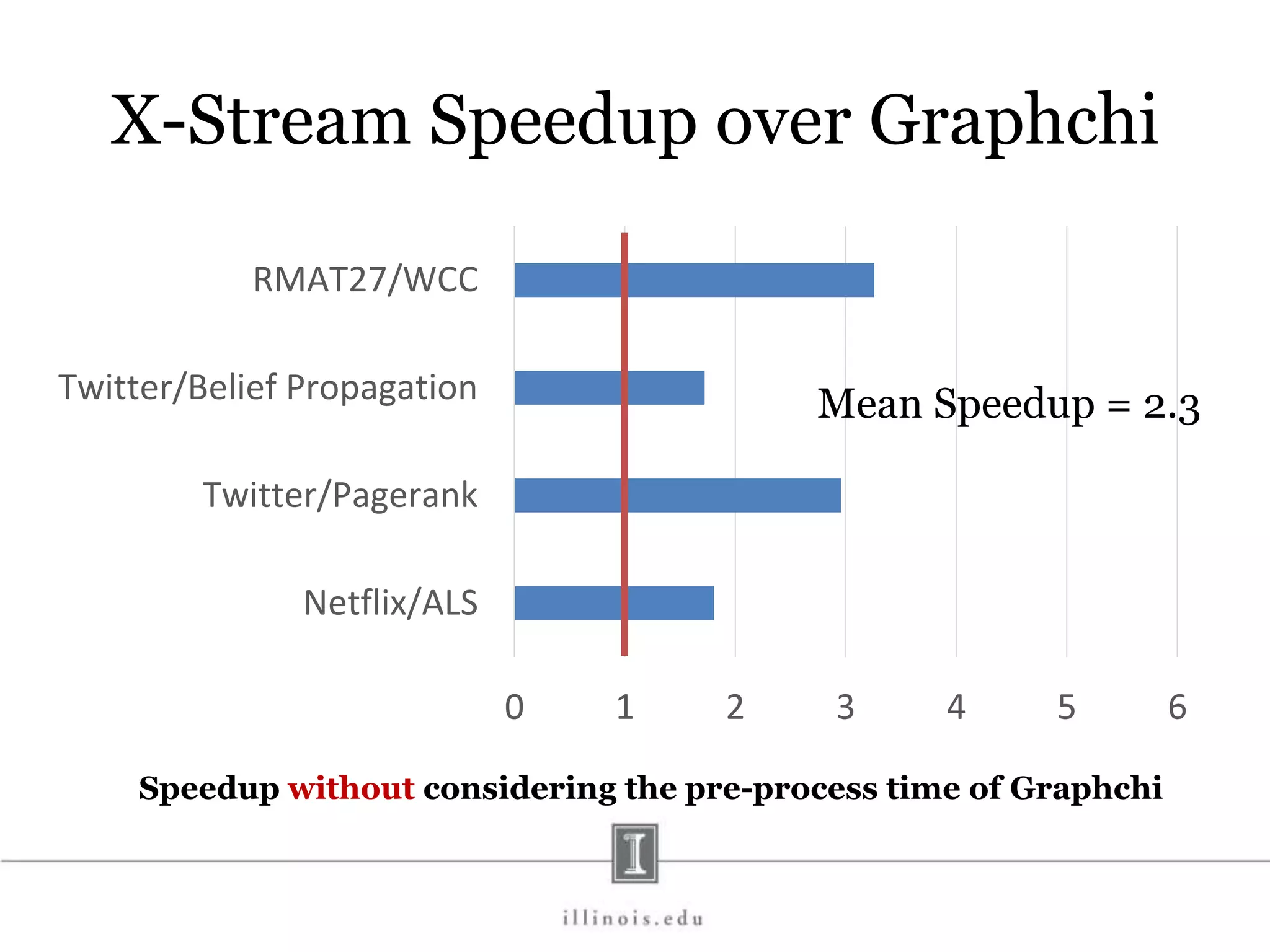
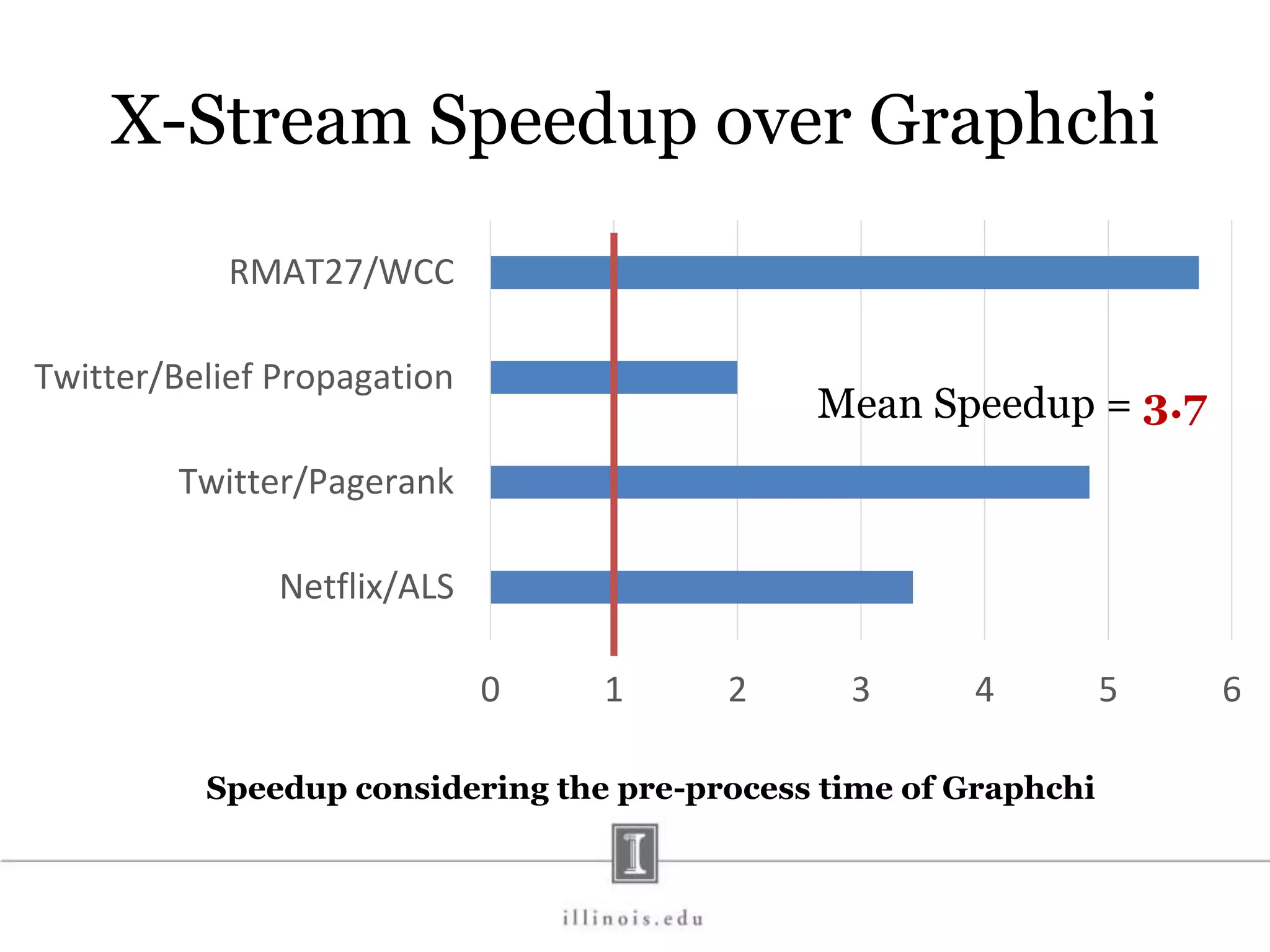


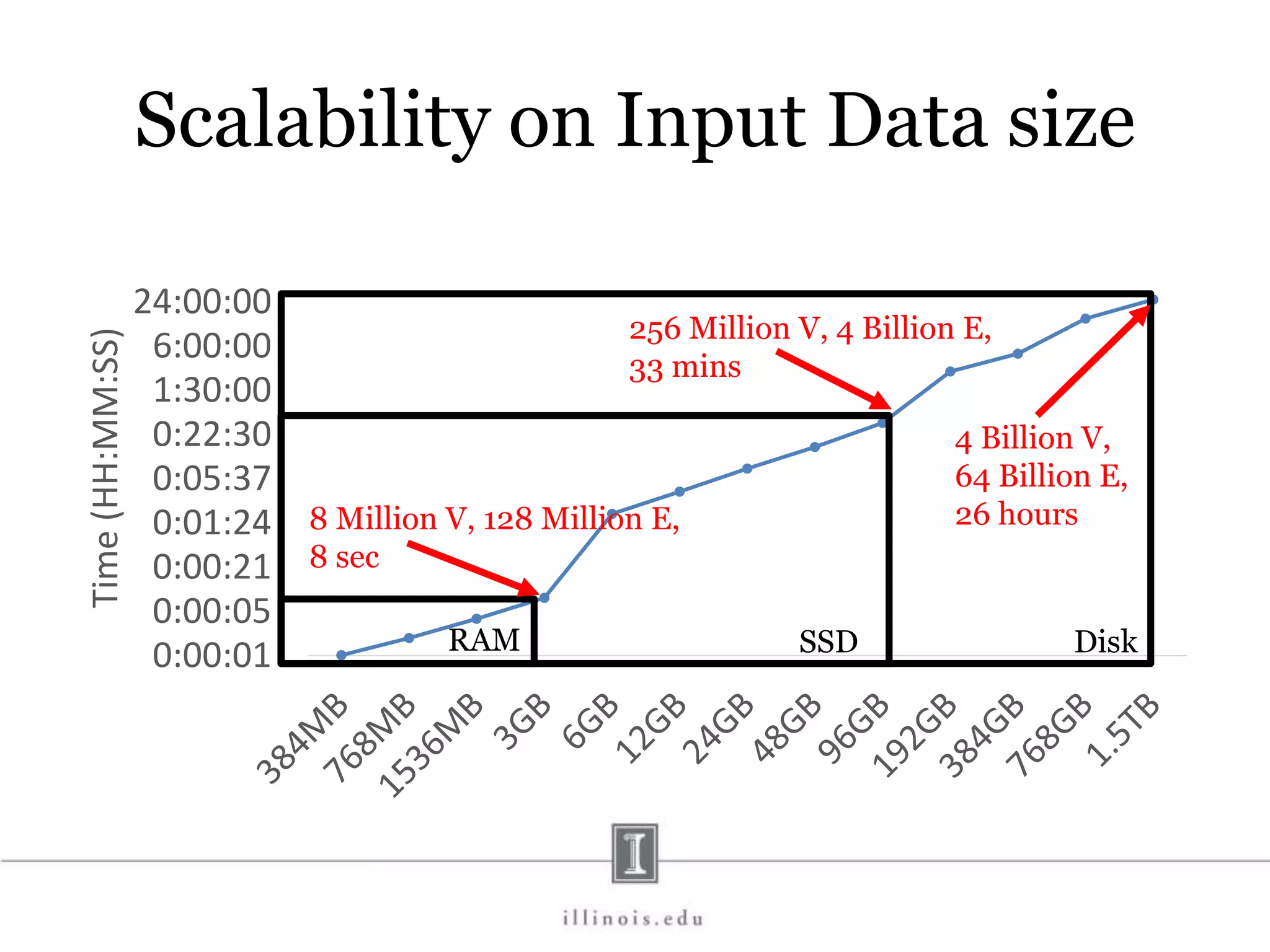





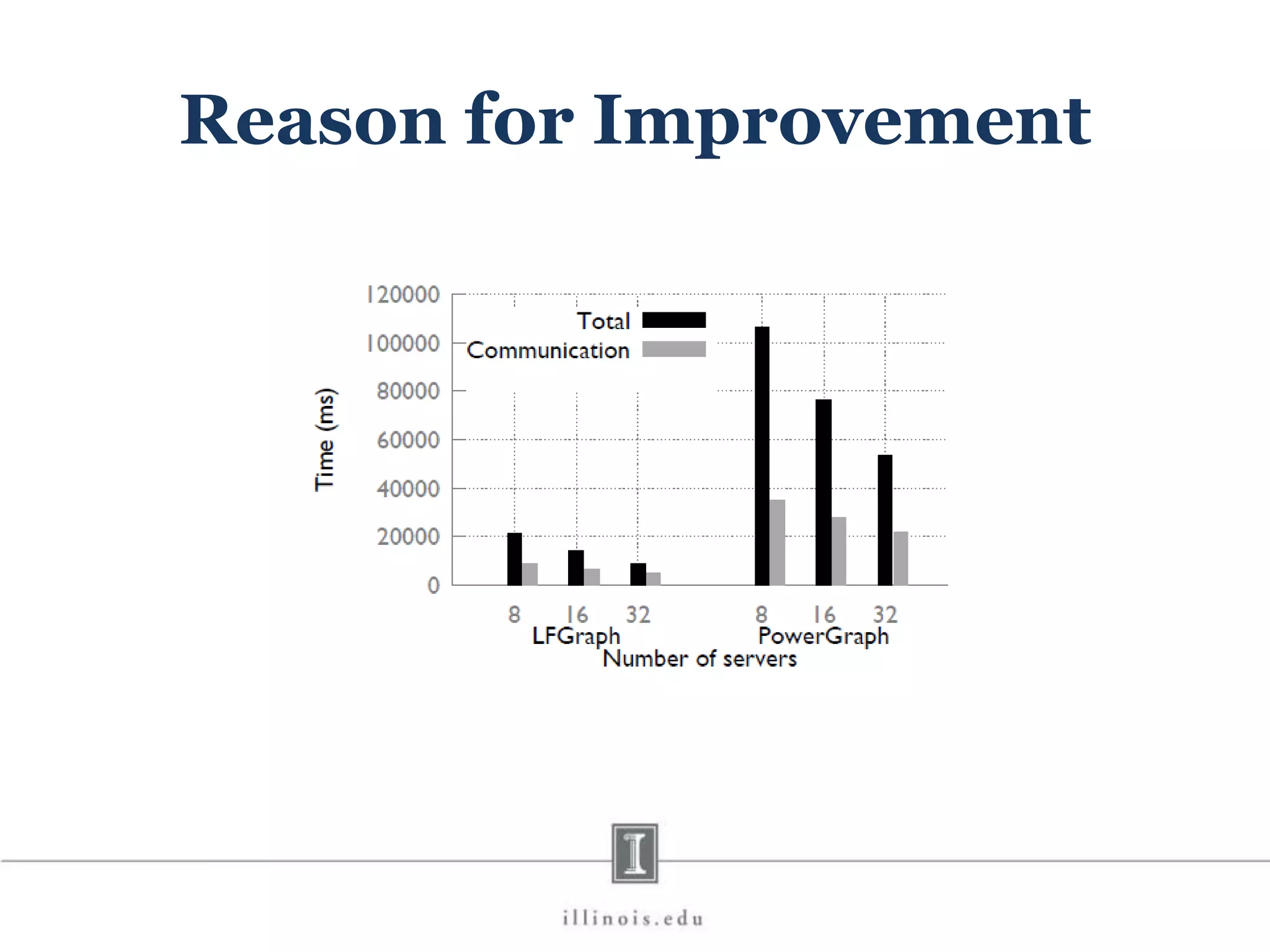

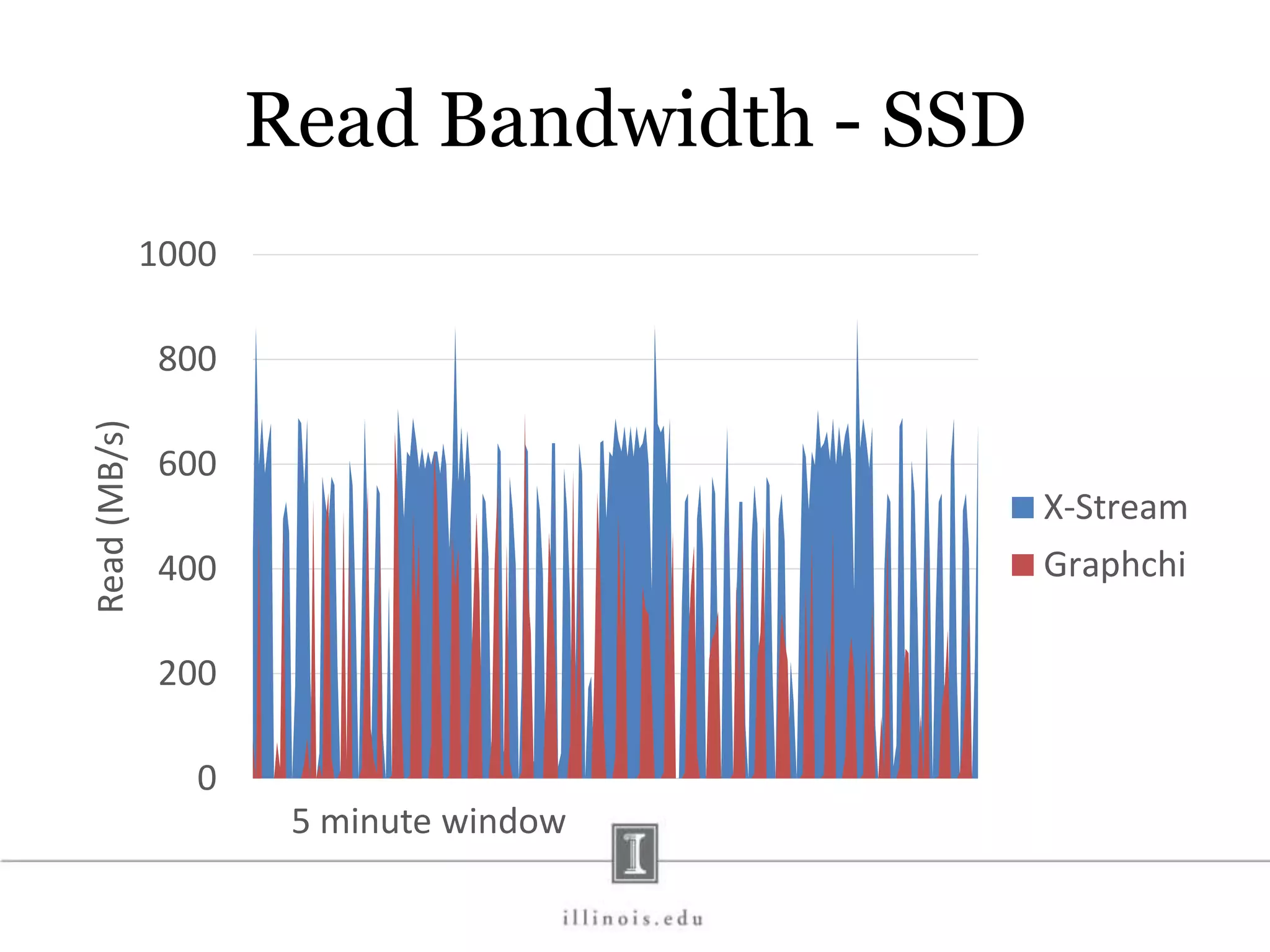
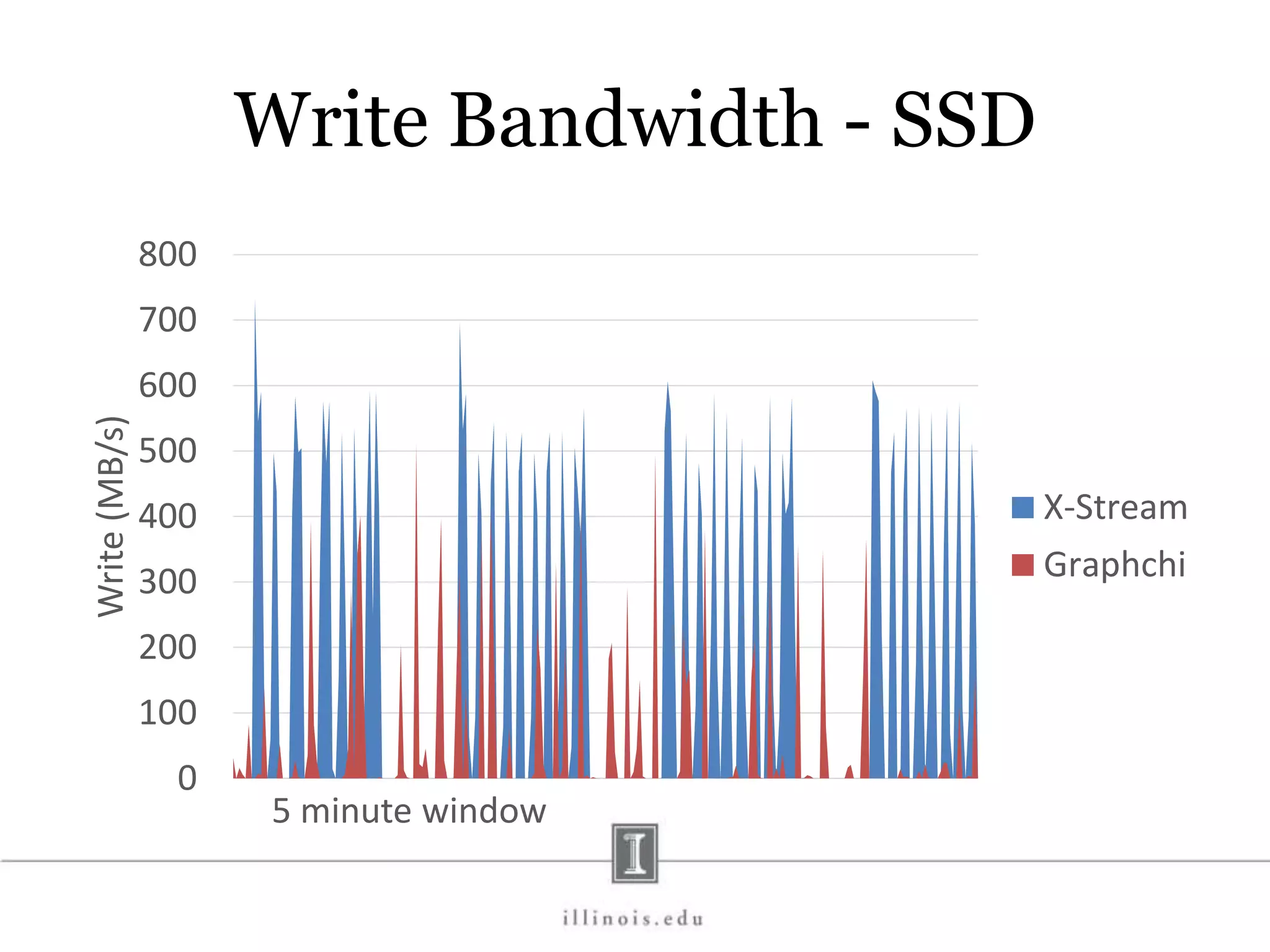
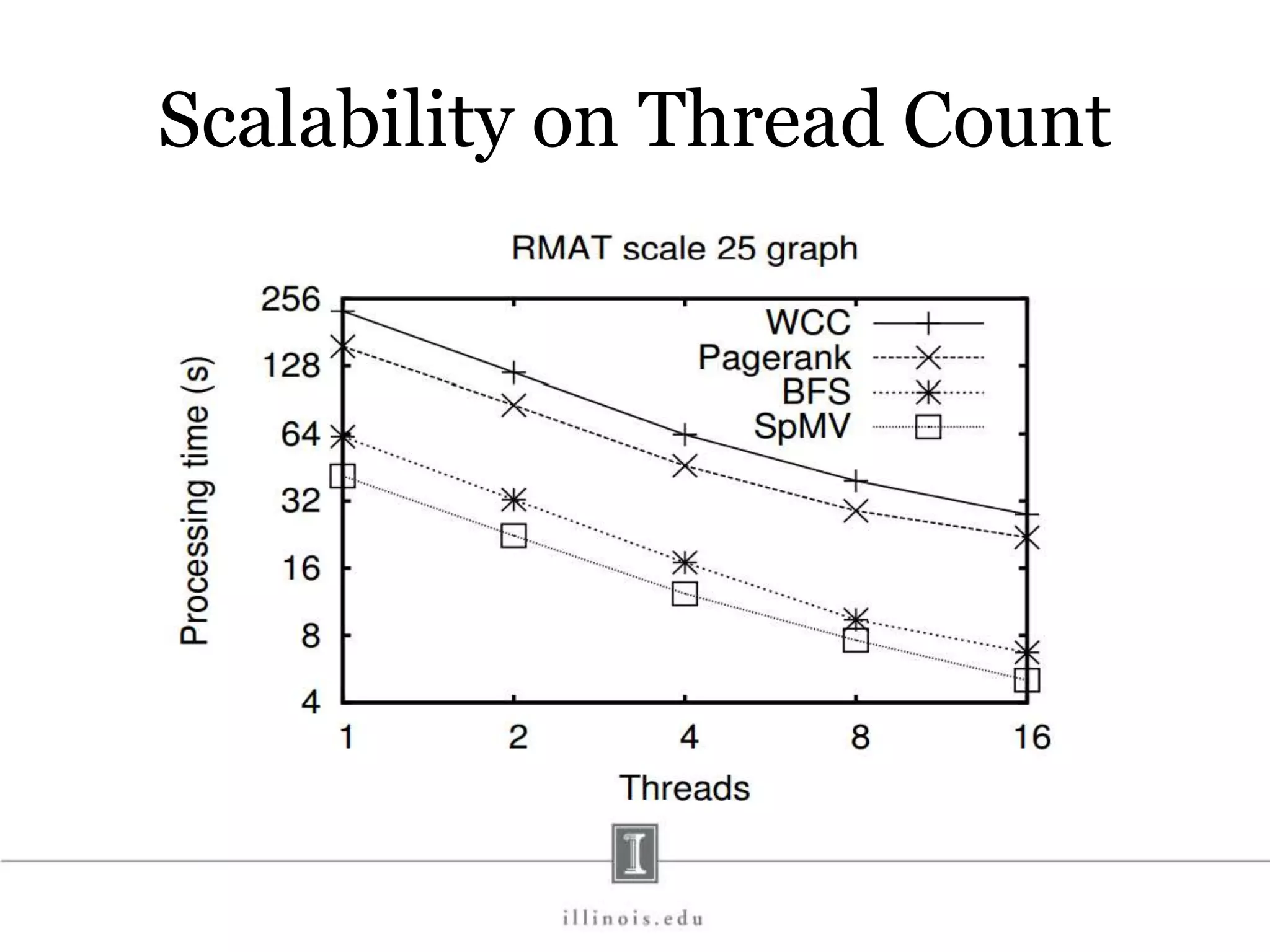
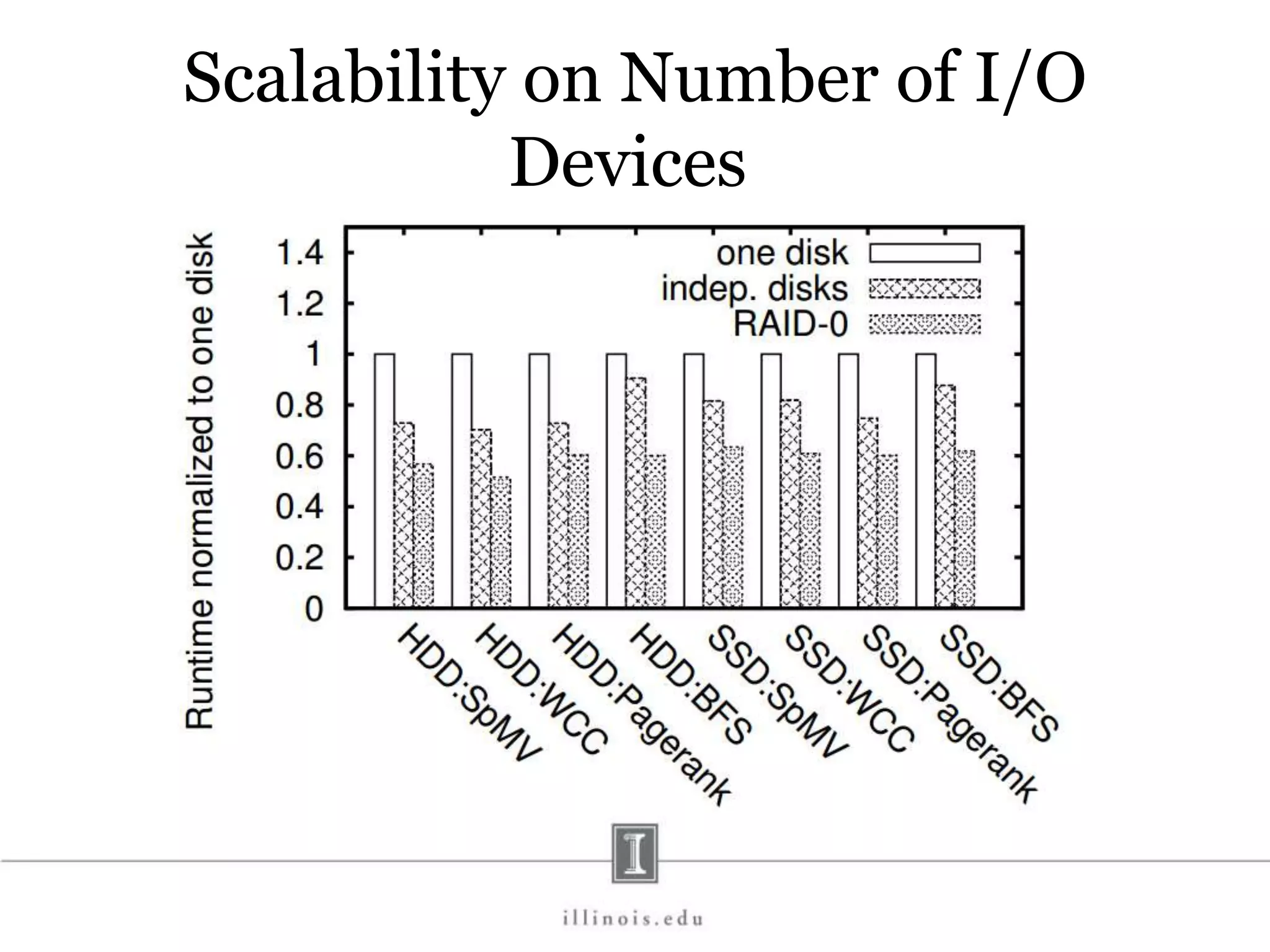

![In-Memory X-Stream Performance 0 50 100 1 2 4 8 16 Runtime(s)Loweris better Threads BFS (32M vertices/256M edges) BFS-1 [HPC 2010] BFS-2 [PACT 2011] X-Stream](https://image.slidesharecdn.com/graphprocessing-150619161603-lva1-app6892/75/Graph-processing-94-2048.jpg)