DIGITAL COMMUNICATION: ENCODING AND DECODING OF CYCLIC CODE

ENCODING AND DECODING OF CYCLIC CODE PREPARED BY:- SHIVANGI SINGH E.C DEPT. SIXTH SEMESTER

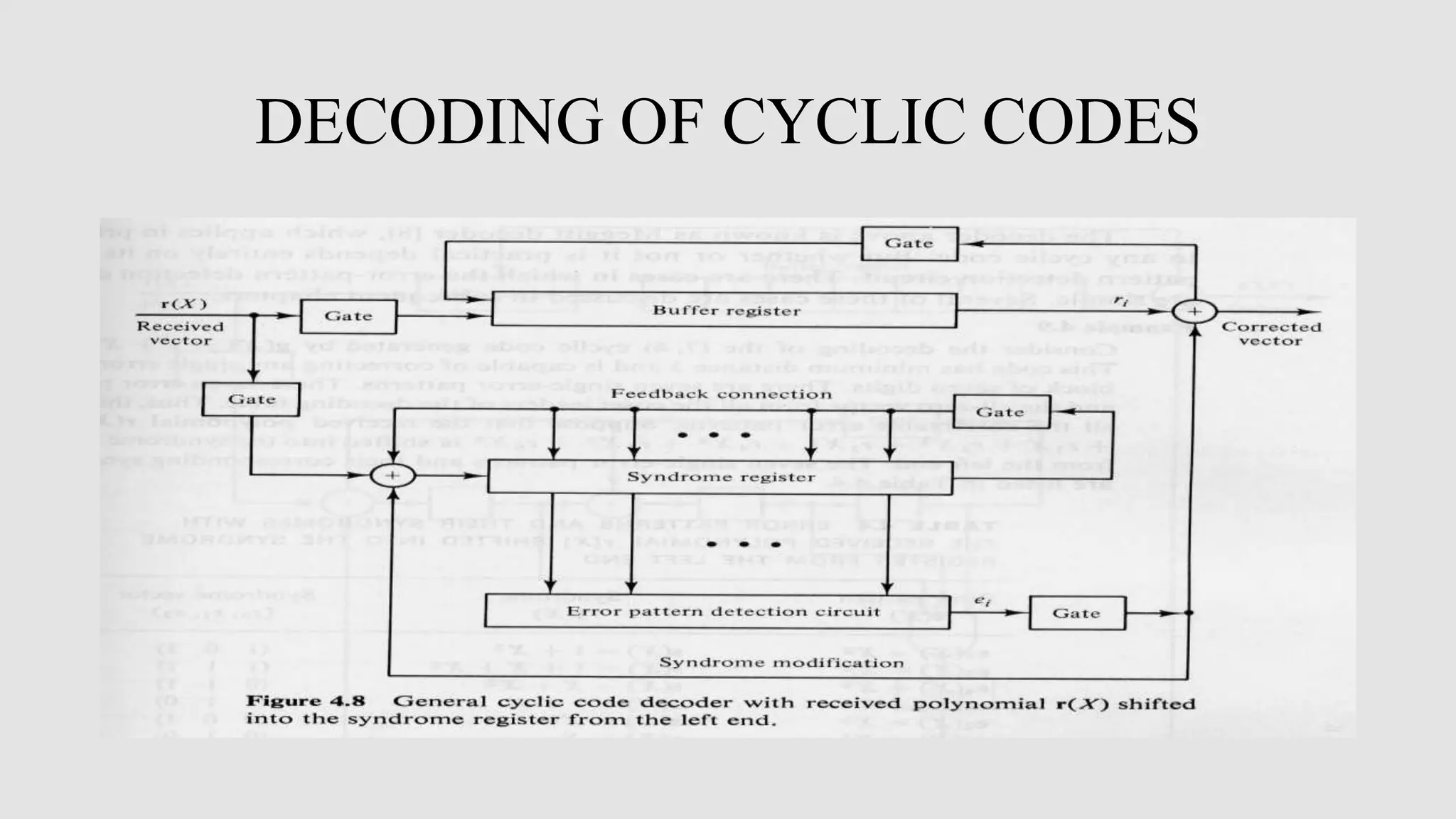
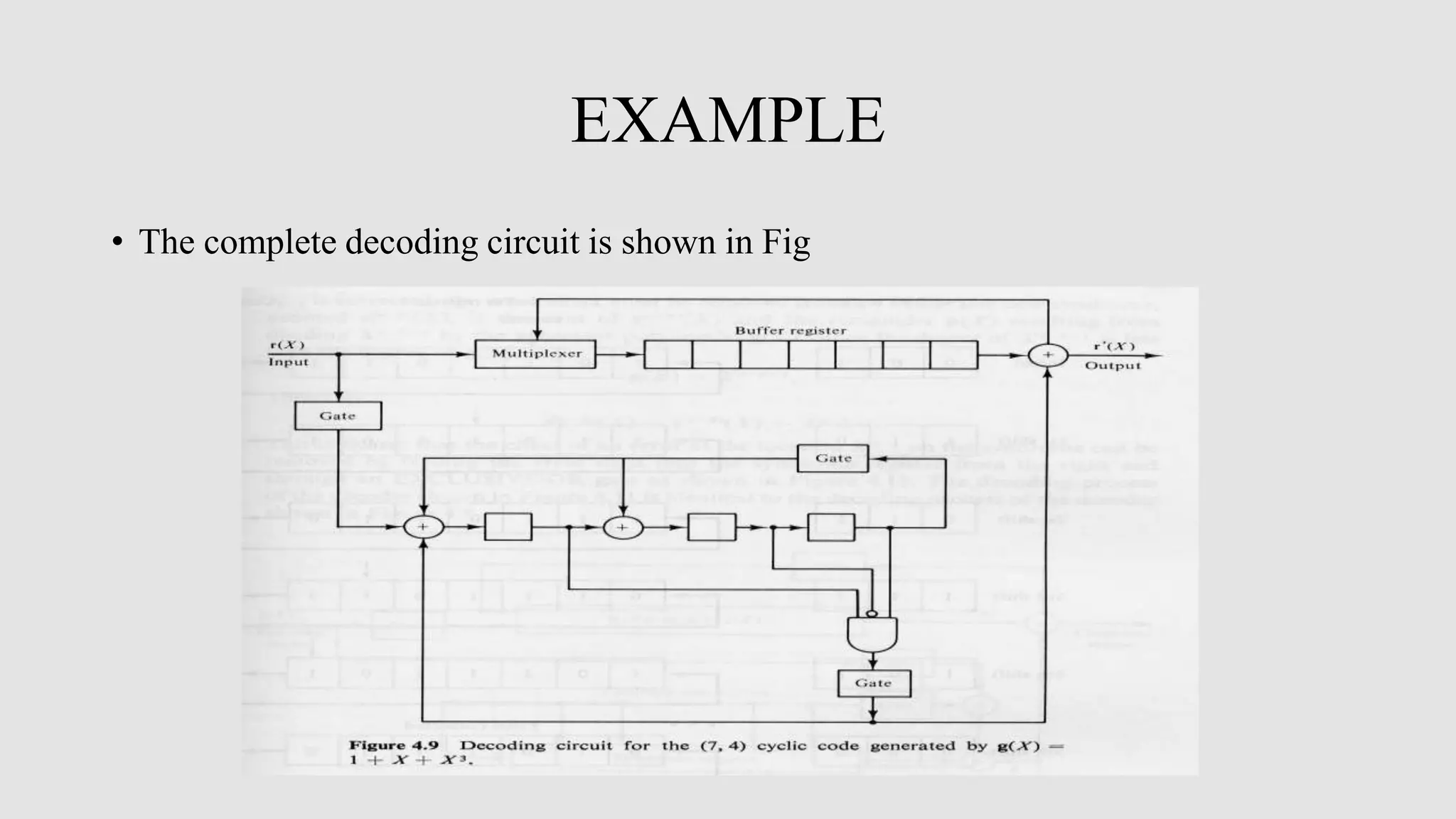
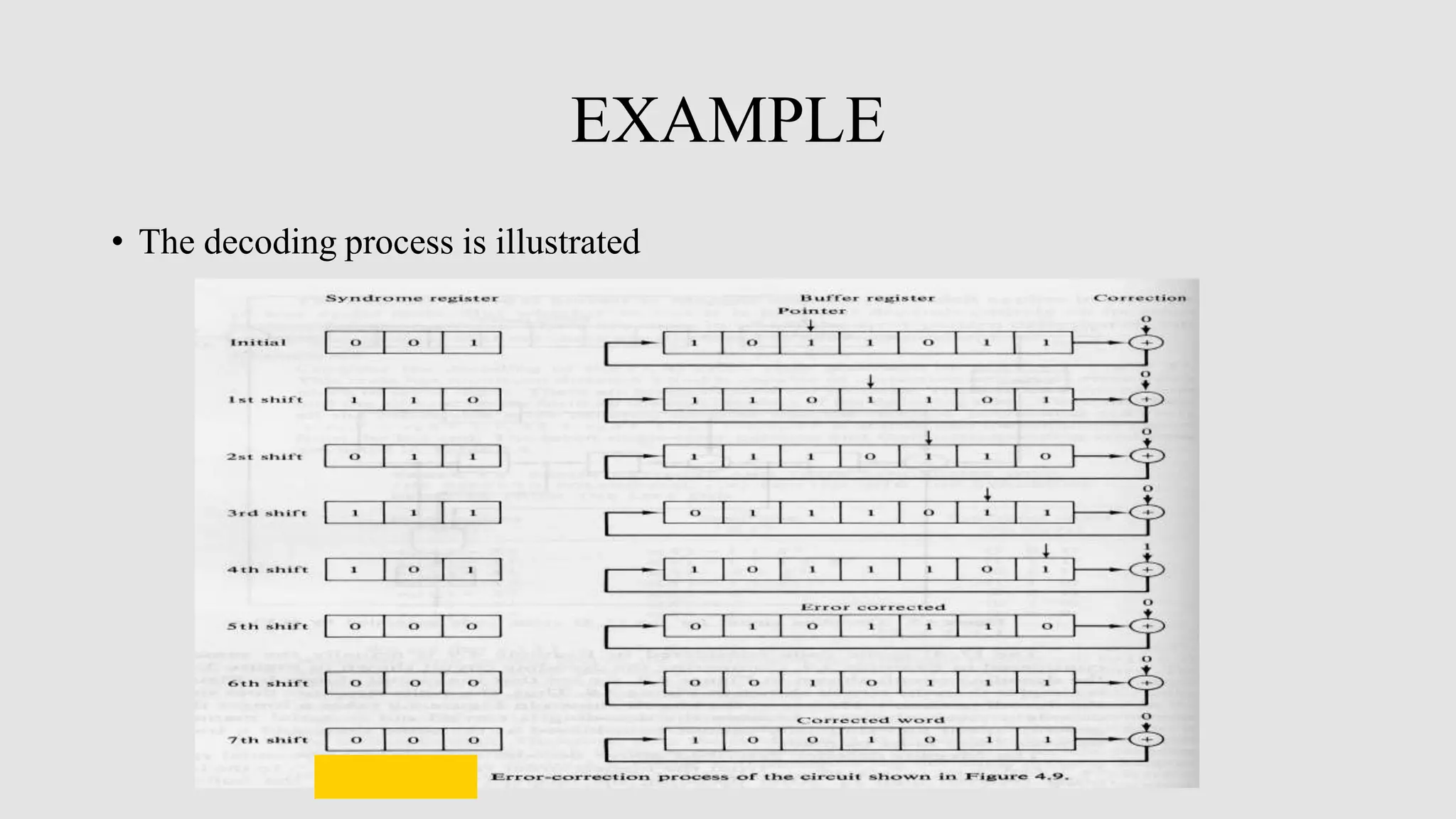
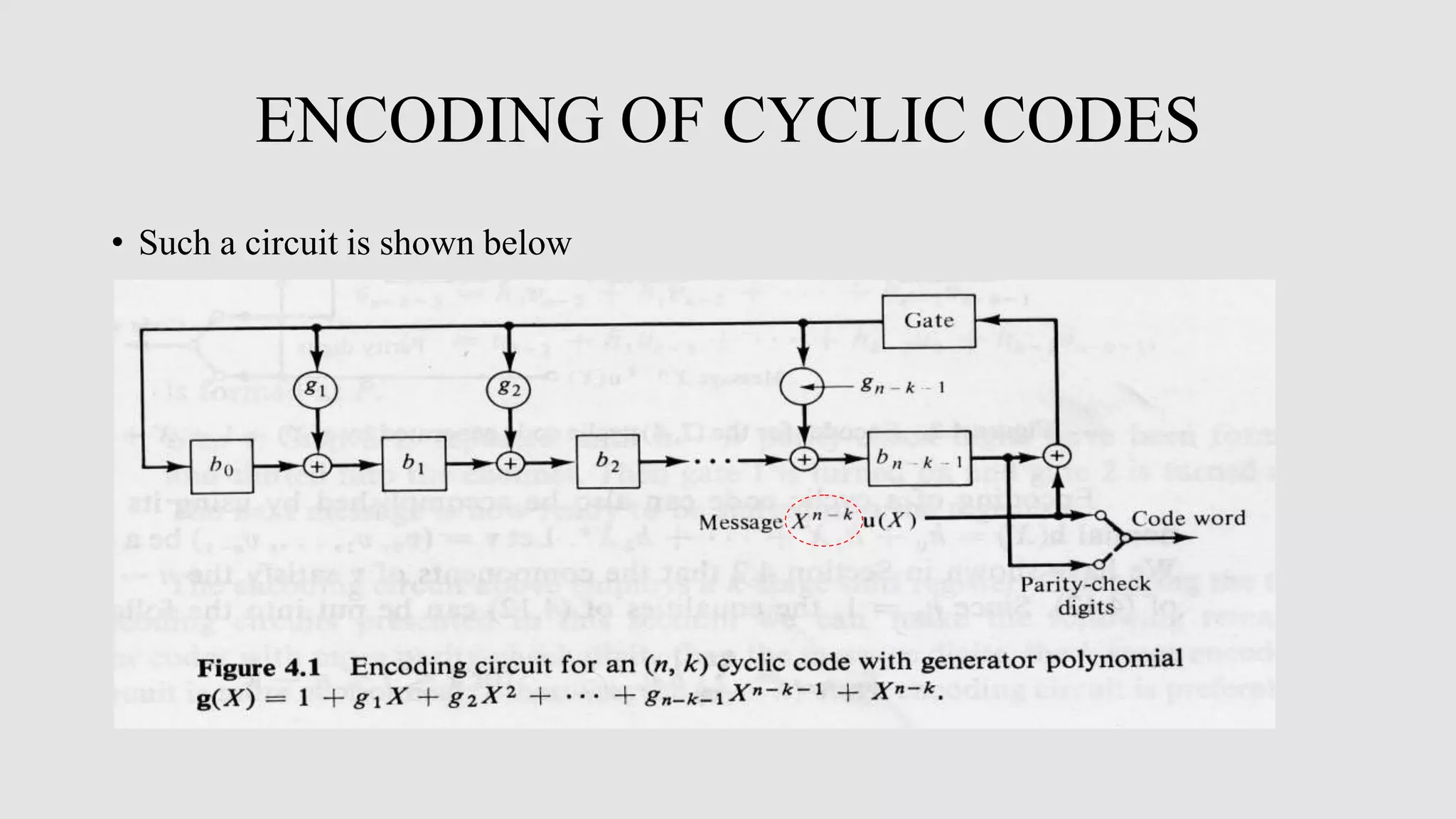
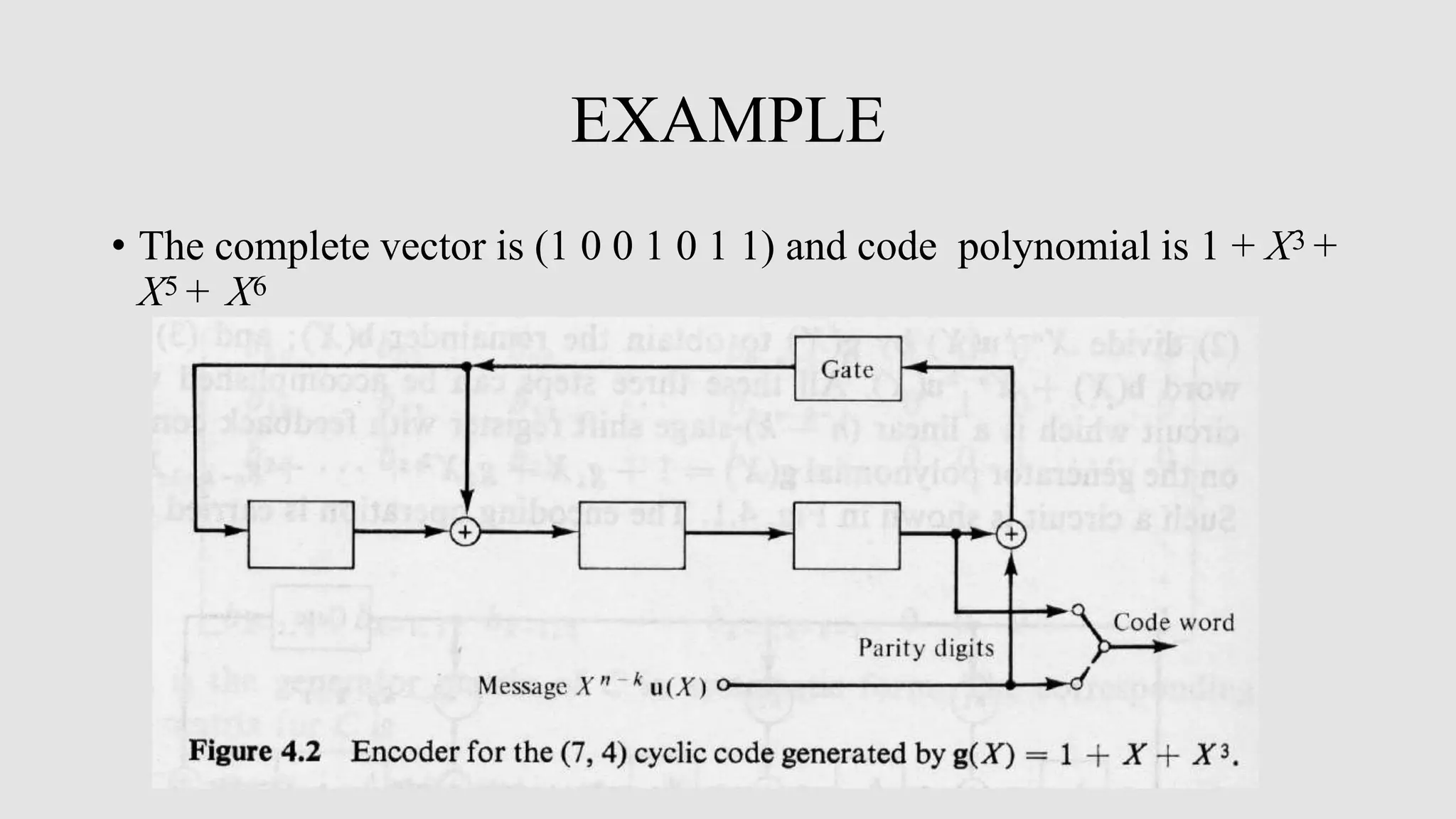
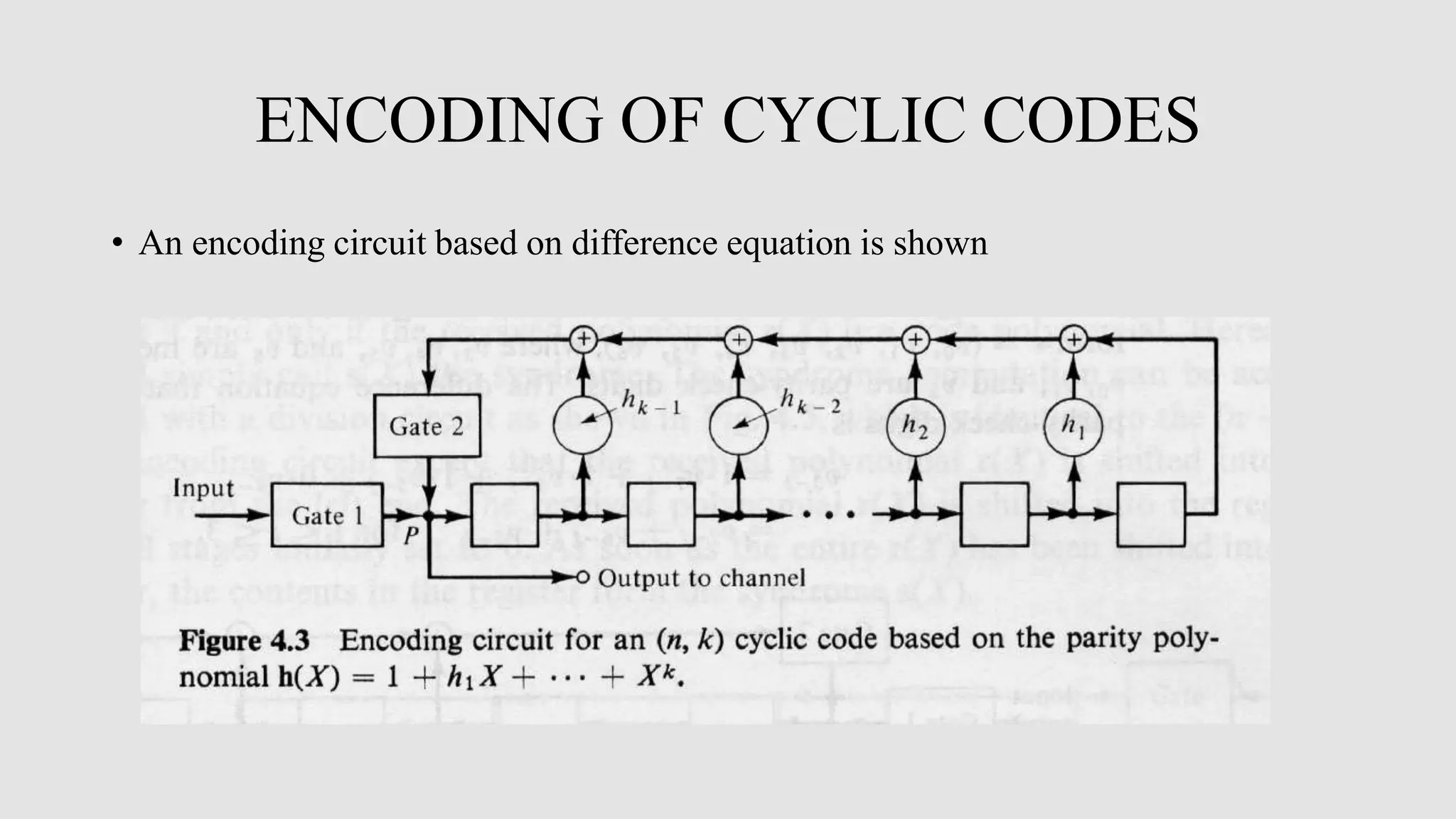
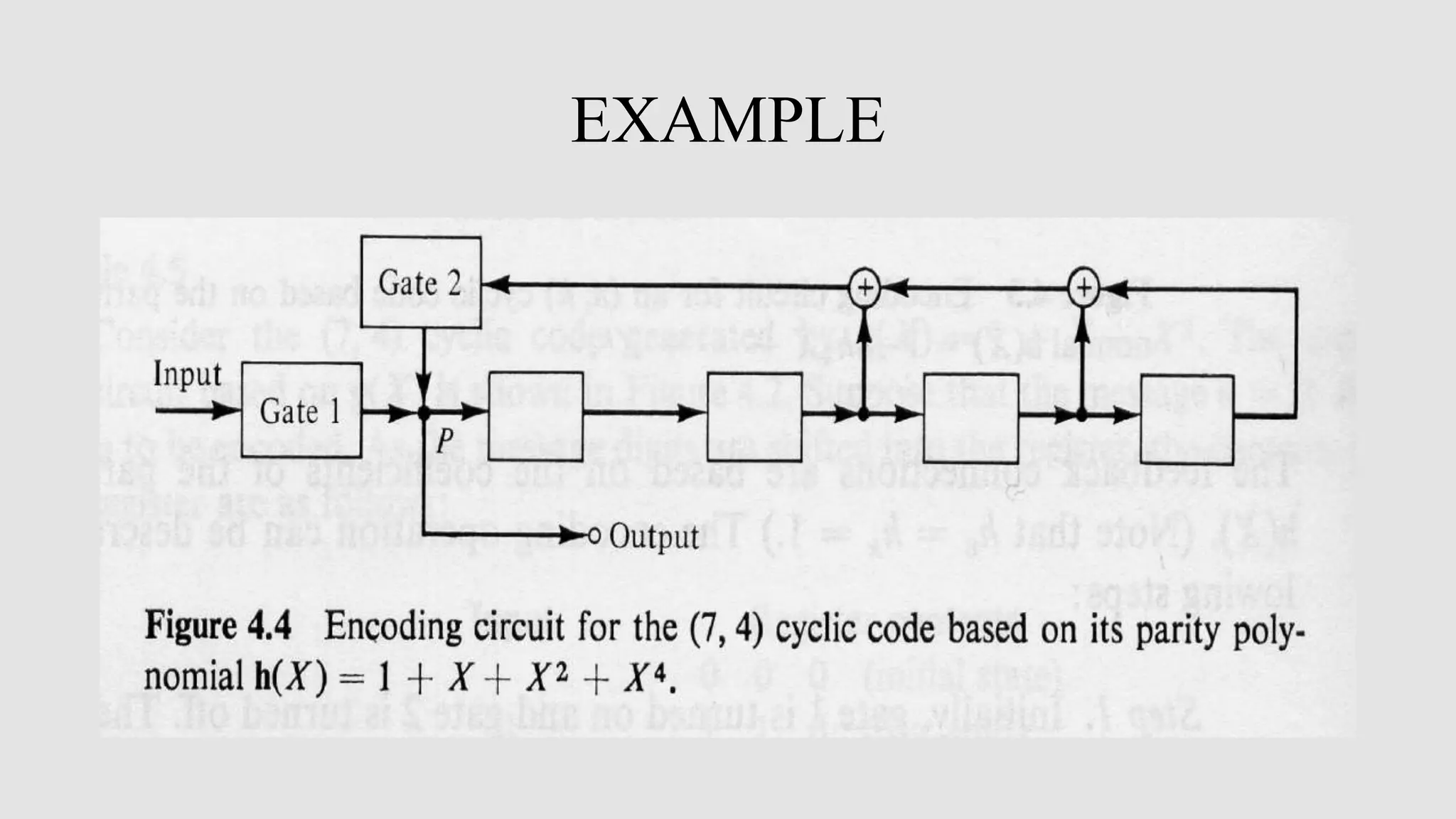
INTODUCTON Cyclic codes form an important subclass of linear codes. These codes are attractive for two reasons: • Encoding and syndrome computation can be implemented easily by employing shift registers with feedback connections (or linear sequential circuits). • Because they have considerable inherent algebraic structure, it is possible to find various practical methods for decoding them.

DESCRIPTION OF CYCLIC CODES • If the n-tuple v = (v0, v1,…, vn-1) are cyclic shifted one place to the right, we obtain another n-tuple • v(1) = (vn-1, v0, v1,…,vn-2) which is called a cyclic shift of v • If the v are cyclically shifted i places to the right, we have v(i) = (vn–i, vn–i+1,…, vn-1, v0, v1, …,vn-i-1) • Cyclically shifting v i places to the right is equivalent to cyclically shifting v (n – i) place to the left

DESCRIPTION OF CYCLIC CODES Definition An (n, k) linear code C is called a cyclic code if every cyclic shift of a code vector in C is also a code vector in C • The (7, 4) linear code given in Table is a cyclic code • To develop the algebraic properties of a cyclic code, we treat the components of a code vector v = (v0, v1,…, vn-1) as the coefficients of a polynomial as follows: • v(X) = v0 + v1X + v2X2 + ··· + vn-1Xn-1 • If vn-1 ≠ 0, the degree of v(X) is n –1 • If vn-1 = 0, the degree of v(X) is less than n –1 • The correspondence between the vector v and the polynomial • v(X) is one-to-one

DESCRIPTION OF CYCLIC CODES The code polynomial that corresponds to the code vector v(i) is v(i)(X) = vn-i + vn-i+1X + ··· + vn-1Xi-1 + v0Xi + v1Xi+1 + ··· + vn-i-1Xn-1 Multiplying v(X) by Xi , we obtain Xi v(X) = v0Xi + v1Xi+1 + ··· + vn-i-1Xn-1 + ··· +vn-1Xn+i-1 • The equation above can be manipulated into the following form : Xi v(X) = vn-i + vn-i+1X +··+ vn-1Xi-1 + v0Xi + ··· + vn-i-1Xn-1 + vn-i(Xn+1) + vn-i+1X(Xn+1) + ··· + vn-1Xi-1(Xn+1) = q(X)·(Xn + 1) + v(i)(X)

ENCODING OF CYCLIC CODES • Encoding of an (n, k) cyclic code in systematic form consists of three steps: • Multiply the message polynomial u(X) by Xn-k Divide Xn-ku(X) by g(X) to obtain the remainder b(X) Form the code word b(X) + Xn-ku(X) • All these three steps can be accomplished with a division circuit which is a linear (n–k)-stage shift register with feedback connections based on the generator polynomial g(X) = 1 + g1X + g2X2 + …+ gn-k-1Xn-k-1 + Xn-k

ENCODING OF CYCLIC CODES • Such a circuit is shown below

ENCODING OF CYCLIC CODES Step 1 • With the gate turned on, the k information digits u0, u1, …, uk-1 are shifted into the circuit and simultaneously into the communication channel • Shifting the message u(X) into the circuit from the front end is equivalent to premultiplying u(X) by Xn-k • As soon as the complete message has entered the circuit, the n – k digits in the register form the remainder and thus they are the parity-check digits Step 2 • Brake the feedback connection by turning off the gate Step 3 • Shift the parity-check digits out and send them into the channel These n – k parity- check digits b0, b1, …, bn-k-1, together with the k information digits, form a complete code vector

EXAMPLE • Consider the (7, 4) cyclic code generated by g(X) = 1 + X + X3 The encoding circuit based on g(X) is shown in Fig. Suppose that the message u = (1 0 1 1) is to be encoded • As the message digits are shifted into the register, the contents in the register are as follows: • After four shift, the contents of the register are (1 0 0) Input Register contents 0 0 0 (initial state) 1 1 1 0 (first shift) 1 1 0 1 (second shift) 0 1 0 0 (third shift) 1 1 0 0 (fourth shift)

EXAMPLE • The complete vector is (1 0 0 1 0 1 1) and code polynomial is 1 + X3 + X5 + X6

ENCODING OF CYCLIC CODES • Encoding of a cyclic code can also be accomplished by using its parity polynomial h(X) = h0 + h1X + ··· +hkXk • Let v = (v0, v1,…, vn-1) be a code vector Since hk = 1, the equalities of can be put into the following form: which is known as a difference equation. • Given the k information digits, it is a rule to determine the n – k parity-check digits, v0, v1, …, vn-k-1 vnk  j  hivni j k1 i=0 for 1 j  n  k

ENCODING OF CYCLIC CODES • An encoding circuit based on difference equation is shown

ENCODING OF CYCLIC CODES • The feedback connections are based on the coefficients of the parity polynomial h(X) • The encoding operation can be described in the following steps : Step 1 • initially gate 1 is turned in and gate 2 is turned off • The k information digits u(X) = u0 + u1X + ··· + uk-1Xk-1 are shifted into the register and the communication channel simultaneously

ENCODING OF CYCLIC CODES Step 2 • As soon as the k information digits have entered the shift register, gate 1 is turned off and gate 2 is turned on • The first parity-check digit vn-k-1 = h0vn-1 + h1vn-2 + ··· + hk-1vn-k = uk-1 + h1uk-2 + ··· + hk-1u0 is formed and appears at point P Step 3 • The first parity-check digits is shifted into the channel and is also shifted into the register

ENCODING OF CYCLIC CODES Step 3 (cont.) • The second parity-check digits vn-k-2 = h0vn-2 + h1vn-3 + ··· +hk-1vn-k-1 = uk-2 + h1uk-3 + ··· + hk-2u0 +hk-1vn-k-1 is formed at P Step 4 • Step 3 is repeated until n – k parity-check digits have been formed and shifted into the channel Then gate 1 is turned on and gate 2 is turned off • The next message is now ready to be shifted into the register

EXAMPLE • The parity polynomial of the (7, 4) cyclic code generated by • g(X) = 1 + X + X3 is h(X) = X7 + 1 / 1 + X + X3 = 1 + X + X2 + X4 • The encoding circuit based on h(X) is shown in Fig The difference equation that determines the parity-check digits is v3-j = 1·v7-j+ 1·v6-j + 1·v5-j + 0·v4-j = v7-j+ v6-j + v5-j for 1 ≤j ≤3 • Suppose that the message to be encoded is (1 0 1 1), then v3= 1, v4= 0, v5= 1, v6= 1

EXAMPLE • The first parity-check digits is • v2 = v6 + v5 + v4 = 1 + 1 + 0 = 0 • The second parity-check digits is • v1 = v5 + v4 + v3 = 1 + 0 + 1 = 0 • The third parity-check digits is • v0 = v4 + v3 + v2 = 0 + 1 + 0 = 1 • Thus, the code vector that corresponds to the message (1 0 1 1) is (1 0 0 1 0 1 1)

DECODING OF CYCLIC CODES • Decoding of cyclic code consists of the same three steps as for decoding linear codes: • Syndrome computation • Association of the syndrome to an error pattern • Error correction • The syndrome computation for cyclic codes can be accomplished with a division circuit whose complexity is linearly proportional to the number of parity-check digits (i.e., n – k) • A straightforward approach to the design of a decoding circuit is via a combinational logic circuit that implements the table-lookup procedure

DECODING OF CYCLIC CODES • The limit to this approach is that the complexity of the decoding circuit tends to grow exponentially with the code length and the number of errors that we intend to correct • The cyclic structure of a cyclic code allows us to decode a received vector r(X)=r0+r1X+r2X2+…+rn-1Xn-1 in a serial manner. • The received digits are decoded one at a time and each digit is decoded with the same circuitry. • As soon as the syndrome has been computed, the decoding circuit checks whether the syndrome s(X) corresponds to a correctable error pattern e(X)= e0+ e1X+…+en- 1Xn-1 withan error at the highest-order position Xn-1 (i.e.,en-1=1).

DECODING OF CYCLIC CODES •If s(X) does not correspond to an error pattern with en-1=1, the received polynomial and the syndrome register are cyclically shifted once simultaneously. By doing so, we obtain r(1)(X)=rn-1+r0X+r1X2+…+rn-2Xn-1 and the new contents in the syndrome register form the syndrome s(1)(X) of r(1)(X). • The same decoding circuit will check whether s(1)(X) corresponds to an error pattern with an error at location Xn-1. If the syndrome s(X) does correspond to an error pattern with en-1=1, the first received digit rn-1 is an erroneous digit and it must be corrected. • This correction is carried out by rn-1♁en-1 .

DECODING OF CYCLIC CODES • This correction results in a modified received polynomial • r1(X)=r0+r1X+r2X2+…+(rn-1♁en-1 )Xn-1. • The effect of the error digit en-1 on the syndrome is then removed from the syndrome s(X). • This can be achieved by adding the syndrome of • e’(X)= Xn-1 to s(X). • This sum is the syndrome of the modified received polynomial r1(X). • Cyclically shift r1(X) and the syndrome register once simultaneously. • This shift results in a received polynomial • r1 (1)(X) =(rn-1♁en-1 ) +r0X+…+rn-2Xn-1.

DECODING OF CYCLIC CODES The syndrome s1 (1)(X) of r1 (1)(X) is the remainder resulting from dividing X[s(X)+Xn-1] by the generator polynomial g(X). Since the remainders resulting from dividing Xs(X) and Xn by g(X) are s(1)(X) and 1, respectively, we have s1 (1)(X)= s(1)(X)+1. Therefore, if 1 is added to the left end of the syndrome register while it is shifted, we obtain s1 (1)(X). • A general decoder for an (n, k) cyclic code is shown in Fig. 5.8 It consists of three major parts • A syndrome register • An error-pattern detector • A buffer register to hold the received vector

DECODING OF CYCLIC CODES • To remove the effect of an error digit on the syndrome, we simply feed the error digit into the shift register from the left end through an EXCLUSIVE-OR gate • The decoding operation is described as follows: Step 1 • The syndrome is formed by shifting the entire received vector into the syndrome register • At the same time the received vector is stored into the buffer register Step 2 • The syndrome is read into the detector and is tested for the corresponding error pattern

DECODING OF CYCLIC CODES Step 2 (cont.) • The detector is a combinational logic circuit which is designed in such a way that its output is 1 if the syndrome in the syndrome register corresponds to a correctable error pattern with an error at the highrst-order position Xn–1 • if a “1” appears at the output of the detector, the received symbol in the rightmost stage of the buffer register is assumed to be erroneous and must be corrected • If a “0” appears at the output of the detector, the received symbol at the rightmost stage of the buffer register is assumed to be correct and no correction necessary • The output of the detector is the estimated error value for the symbol to come out of the buffer

DECODING OF CYCLIC CODES Step 3 • The first received symbol is read out of the buffer • If the first received symbol is detected to be an erroreous symbol, it is corrected by the output of the detector • The output of the detector is fed back to the syndrome register to modify the syndrome • This results in a new syndrome, which corresponds to the altered received vector shifted one place to the right Step 4 • The new syndrome formed in step 3 is used to detect whether or not the second received symbol is an erroneous symbol • The decoder repeats step 2 and 3

DECODING OF CYCLIC CODES Step 5 • The decoder decodes the received vector symbol by symbol in the manner outlined above until the entire received vector is read out of the buffer register • The decoder above is known as Meggitt decoder

EXAMPLE • Consider the decoding of the (7, 4) cyclic code generated by g(X) = 1 + X + X3 • This code has minimum distance 3 and is capable of correcting any single error over a block of seven digits • There are seven single-error patterns • These seven error patterns and the all-zero vector form all the coset leader of the decoding table

EXAMPLE • They form all the correctable error patterns Suppose that the received polynomial • r(X) = r0 + r1X +r2 X2 + … + r6 X6 •is shifted into the syndrome register from the left end The seven single-error patterns and their corresponding syndromes are listed in Table

EXAMPLE • The complete decoding circuit is shown in Fig

EXAMPLE • The decoding process is illustrated

DIGITAL COMMUNICATION: ENCODING AND DECODING OF CYCLIC CODE

More Related Content

What's hot

Similar to DIGITAL COMMUNICATION: ENCODING AND DECODING OF CYCLIC CODE

More from ShivangiSingh241

Recently uploaded

In this document

DIGITAL COMMUNICATION: ENCODING AND DECODING OF CYCLIC CODE