Controller Design Based On Fuzzy Observers For T-S Fuzzy Bilinear Models

Controller Design Based On Fuzzy Observers For T-S Fuzzy Bilinear Models

• 1.
  International Journal ofControl Theory and Computer Modeling (IJCTCM) Vol.6, No.1/2, April 2016 DOI : 10.5121/ijctcm.2016.6201 1 CONTROLLER DESIGN BASED ON FUZZY OBSERVERS FOR T-S FUZZY BILINEAR MODELS Dhikra Saoudi LSA - Laboratoire des Systèmes Avancés, Polytechnic High School of Tunisia, University of Carthage, BP 743, 2078 La Marsa, Tunisia. ABSTRACT This article is devoted to the design of a fuzzy-observer-based control for a class of nonlinear systems with bilinear terms. The class of systems considered is the Takagi-Sugeno (T-S) fuzzy bilinear model. A new procedure to design the observer-based fuzzy controller for this class of systems is proposed. The aim is to design the fuzzy controller and the fuzzy observer of the augmented system separately in order to guarantee that the error between the state and its estimation converges faster to zero. By using the Lyapunov function, sufficient conditions are derived such that the closed-loop system is globally asymptotically stable. Moreover, sufficient conditions for controller design based on state estimation for robust stabilization of T- S FBS with parametric uncertainties is proposed. The observer and controller gains are obtained by solving some linear matrix inequalities (LMIs). An example is given to illustrate the effectiveness of the proposed approach. Keywords T-S fuzzy bilinear model, Fuzzy observer-based control, Lyapunov function, Parametric uncertainty, LMI. 1. INTRODUCTION In recent years, the stability analysis and the synthesis of controllers/observers for nonlinear systems have been the subject of many research works. In recent years, the stability analysis and the synthesis of controllers/observers for nonlinear systems are still open problems owing to their nature complexity and have been the subject of many research works. It is well known that Takagi-Sugeno (T-S) fuzzy model is a modelling method [1] that can represent or approximate a large class of nonlinear systems by a set of local linear dynamics [2]. Various results have been devoted to the stability analysis and stabilization of T-S fuzzy systems [3]-[7]. These results use different techniques such as the system parameters to be known but in reality the parameters of the system can be either uncertain or time-dependent. Moreover, the problem of stabilization remains an important issue in the controller designs of uncertain nonlinear systems [8], [9]. It is also necessary to consider the robust stability of uncertain T-S fuzzy models in order to guarantee both stability and the robustness with respect to the latter. The study of robustness in fuzzy model-based control has been studied widely in the literature for nonlinear systems. For example, fuzzy model-based control for T-S fuzzy models has been studied in [10]-[12] and for T-S fuzzy models with parametric uncertainties has been given in [13]-[15]. Moreover, it is noted that all of the aforementioned assume that the system states are measured, which is not true in many control systems and real applications. For this reason, observer-based fuzzy controllers were considered
• 2.
  International Journal ofControl Theory and Computer Modeling (IJCTCM) Vol.6, No.1/2, April 2016 2 in many researches. In [16]-[18], the authors have studied the controller designs based on fuzzy observers for T-S fuzzy systems. Nonetheless, in [19]-[21], the authors have proposed sufficient design conditions for robust stabilization of T-S fuzzy models with parametric uncertainties based on state estimation. In recent years, the fuzzy bilinear systems (FBS) based on the T-S fuzzy model with bilinear rule consequence were considered in [22]-[24]. It is proved in these papers that often nonlinear behaviours can be approximated by T-S bilinear multimodel description. This modeling method is based on the bilinearization of the nonlinear system around some operating points and using adequate weighting functions. This kind of T-S fuzzy model is especially suitable for a nonlinear system with a bilinear term. Some topics of control are extended to T-S fuzzy bilinear model (FBM). For example; in [22] proposed a fuzzy controller to stabilize the FBS and also for the fuzzy bilinear systems with parametric uncertainties. In [23], [26], the authors studied the robust ∞H control problem for T-S FBS. In [25], the authors developed a static output feedback controller for T-S discrete fuzzy bilinear systems (DFBS). Furthermore, the stabilization problems of T-S FBS and T-S DFBS with time-delay have been proposed in [27],[28]. Moreover, some studies have investigated the observer problem for T–S fuzzy bilinear systems [29]-[34] and application to fault diagnosis and fault tolerant control, have been examined for this class of systems in [35]-[37]. Unfortunately, to the best of our knowledge, no previous study has investigated the problem of an observer-based control for T-S fuzzy bilinear models and a robust stabilization for uncertain T-S fuzzy models. In this paper, an observer-based control design for uncertain nonlinear systems in order to guarantee the closed-loop stability is proposed. The T-S FBM is employed to represent a nonlinear system with parametric uncertainties. This kind of T-S fuzzy model is especially suitable for a nonlinear system with a bilinear term. The goal is to design the fuzzy controller and the fuzzy observer of the augmented system separately in order to guarantee that the error between the state and its estimation converges faster to zero. By employing the Lyapunov function, design conditions are derived. The gains of the observer and the controller are obtained by solving some linear matrix inequalities. So, this paper brings some results for the observer- based control design dedicated to fuzzy bilinear models and uncertain fuzzy bilinear models. This paper is organized as follows. In section 2, the considered structure of the T-S fuzzy bilinear system is presented. In Section 3, the problem of observer-based control for the fuzzy bilinear systems is developed. In section 4, the method of controller design based on state estimation for robust stabilization of T-S FBS with parametric uncertainties is proposed. an illustrative example is provided to show the effectiveness of the proposed approach in Section 5. Finally, Section 6 concludes the paper. 2. T-S FUZZY BILINEAR MODEL REPRESENTATION In a fuzzy modelling framework, the fuzzy bilinear models based on the T-S fuzzy model with bilinear rule consequence were an extension of the T-S fuzzy ordinary model. It is proved that often nonlinear behaviours can be approximated by T-S fuzzy bilinear model description. This technique is based on the bilinearization of the nonlinear system around some operating points and using adequate weighting functions. This kind of T-S fuzzy model is especially suitable for a nonlinear system with a bilinear term. Then, the fuzzy bilinear model is described by the following fuzzy if-then rules: 1 1: if ( ) is and and ( ) isLi i g igR t F t Fξ ξ
• 3.
  International Journal ofControl Theory and Computer Modeling (IJCTCM) Vol.6, No.1/2, April 2016 3 then ( ) ( ) ( ) ( )u(t) ( ) ( ) = + +  = & i i ix t A x t Bu t N x t y t Cx t (1) where iR denotes the th i fuzzy rule $ { }1, ,∀ = Li r , r is the number of if-then rules, ( )i tξ are the premise variables which can be measurable or not measurable, and ( (t))ij jF ξ are fuzzy set. ( )∈ℜn x t is the state vector, ( )∈ℜu t is the control input, and ( )∈ℜp y t is the system output. The matrices , , ,i i iA B N C are known matrices. Then, the overall FBM can be described as follows: ( ) 1 ( ) ( ( )) ( ) ( ) ( )u(t) ( ) ( ) =  = + +   = ∑& r i i i i i x t h t A x t Bu t N x t y t Cx t ξ (2) where (.)ih verify the following properties: { }1 ( ( )) 1 1,2, , 0 ( ( )) 1 =  = ∀ ∈  ≤ ≤ ∑ L r i i i h t i r h t ξ ξ (3) Remark 1: Matrices , ,i i iA B N and C can be obtained by using the polytopic transformation [2]. The advantage of this method is in one hand to lead to a bilinear transformation of the nonlinear model without any approximation error, and in another hand to reduce the number of local models compared to other methods [22]. 3. CONTROL OF THE FUZZY BILINEAR MODEL In this section, we will develop the observer-based control problem for the fuzzy bilinear systems. Thereafter, we will propose sufficient conditions that guarantees the closed-loop stability by using a Lyapunov function-based design approach. The goal is to design the fuzzy controller and the fuzzy observer of the augmented system separately in order to guarantee that the error between the state and its estimation converges faster to zero. Many studies consider that all the state variables of the system are available. However in practice this assumption often does not hold. Hence, we need to define a fuzzy observer to estimate the states and make an analysis of the error system, from which we provides a design method of a fuzzy observer for the fuzzy bilinear system (2). Then, the proposed structure of the fuzzy bilinear observer has the following form:. Then, the proposed structure of the fuzzy bilinear observer has the following form: ( )( ) 1 ˆ ˆ ˆ ˆ( ) ( ( )) ( ) ( ) ( )u(t) ( ) ( ) ˆ ˆ( ) ( ) =  = + + + ϒ −   = ∑& r i i i i i i x t h t A x t Bu t N x t y t y t y t Cx t ξ (4)
• 4.
  International Journal ofControl Theory and Computer Modeling (IJCTCM) Vol.6, No.1/2, April 2016 4 where ˆ( )x t is the estimated state vector of ( )x t , and , 1, ,ϒ = Li i r are observer parameters to be determined. In this paper, it is assumed that all of the premise variables do not depend on the state variables estimated by a fuzzy observer. Following the design concept in [38], the fuzzy control law for FBM is formulated as follows: ( ) ( ) ( ) 1 1 1 ˆ( ) ( ) ( ) ˆ ˆ1 ( ) ( ) ˆ( ) sin ( ) ˆˆ( ) ( )cos ( ) = = = = + = = ∑ ∑ ∑ r i i T T i i i r i i i r i i i i D x t u t h t x t D D x t h t t h t D x t t ρ ξ ξ ρ θ ξ ρ θ (5) where: ˆ( ) 1ˆ ˆsin ( ) , cos ( ) ˆ ˆ ˆ ˆ1 ( ) ( ) 1 ( ) ( ) ˆ , 2 2 = = + +   ∈ −    i i iT T T T i i i i i D x t t t x t D D x t x t D D x t θ θ π π θ ρ is a given scalar, and 1 , 1, ,r× ∈ℜ = Ln iD i are vectors to be determined. Let us define the state estimation error: ( ) ( ) ( )ˆ= −e t x t x t (6) Then, one can obtain the fuzzy observer error dynamics from (2), (4), and (5): ( ) ( ) ( )( )1 1 ˆ( ) ( ) ( ) + sin ( ) ( ) = = = + ϒ∑∑& r r i j i i i j i j e t h t h t A C N t e tξ ξ ρ θ (7) Let us define the augmented system containing both the fuzzy controller and observer    TT T x e which dynamics is given by the augmented system: ( ) ( ) ( ) ( ) ( ) ( )     =        & & x t x t A t e t e t ξ (8)
• 5.
  International Journal ofControl Theory and Computer Modeling (IJCTCM) Vol.6, No.1/2, April 2016 5 where the matrices ( )( )A tξ are given by: ( ) ( ) ( ) 1 1 ( ) ( ) ( ) = = = ∑∑ r r i j ij i j A t h t h t Aξ ξ ξ with: ˆ ˆ ˆsin cos cos ˆ0 sin  + + =   + ϒ +   i i j i j j i j j ij i i i j A N B D B D A A C N ρ θ ρ θ ρ θ ρ θ The goal is to design the observer-based fuzzy controller (5) for the fuzzy bilinear system (2) such that the closed-loop augmented system (8) becomes globally asymptotically stable. Therefore, the main result is then propounded in the following theorem. Theorem 1: If there exist symmetric positive definite matrices 1P and 2P , matrices ,i iW V and positive scalars 0 , 0> >ε ρ such that LMIs (9) and (10) are satisfied, then the augmented system described by (8) is asymptotically stable 1 , 1∀ = ∀ =L Li r j r 1 1 1 * * * * * * * 00 * * 0 0 * 0 0 0  +   −    <−   −   −  T i i i i j T i A P PA N P I BV I I I B I ρ ε (9) 2 2 2 1 * * * * * 0 0 * 0 0 −  + + +   −  <  −   −   T T T i i i i i j P A A P WC C W P N I I I D I ρ ε (10) The gains of the observer and the state feedback control law are given by: 1 1 − =i iD V P (11) 1 2 − ϒ =i iP W (12) Proof: In order to ensure the global, asymptotic stability, a new procedure for designing the observer-based fuzzy controller (5) for the fuzzy bilinear system (2) is proposed such that the closed-loop system (8) becomes asymptotically robust stable by using a Lyapunov function-based design approach. Then from (8), the sufficient conditions must be verified: ( )0 , , 0∃ = > = + <T D T ij ij ij ijQ Q M A Q A Q QA (13)
• 6.
  International Journal ofControl Theory and Computer Modeling (IJCTCM) Vol.6, No.1/2, April 2016 6 Where 11 22 0 0   =     Q Q Q (14) Let us define ( ) 1 2 , = +D D D ij ij ij ijM A Q M M (15) with 11 21 1 2 12 22 0 0 , 0 0     = =           ij ijD D ij ij ij ij D D M M D D (16) ( ) ( ) ( ) 11 11 11 11 11 11 11 12 22 22 22 22 22 22 21 22 22 22 ˆ ˆsin sin ˆ ˆcos cos ˆ ˆsin sin ˆcos ˆcos = + + + + + = + + + + ϒ + ϒ = = T T ij i i i j i j T i j j i j j T T ij i i i j i j T i i ij i j j T ij i j j D AQ Q A N Q Q N Q B D B D Q D AQ Q A N Q Q N CQ Q C D B D Q D Q B D ρ θ ρ θ ρ θ ρ θ ρ θ ρ θ ρ θ ρ θ (17) In order to investigate the stability criteria, the following lemma will be also used [39]. Lemma 1: For any matrices A and B with appropriate dimensions, the following property holds for any positive scalar λ : 1− + ≤ +T T T T A B B A A A B Bλ λ (18) Let 11 1=Q P and 1 22 2 − =Q P . From (16) and by using the separation Lemma (1) [40], one obtains: ( ) 1 2 0 , 0   ≤      ijD ij ij ij R M A Q R (19) In order to verify (13), we must have: 1 2 0 0 0   <     ij ij R R (20)
• 7.
  International Journal ofControl Theory and Computer Modeling (IJCTCM) Vol.6, No.1/2, April 2016 7 Which implies : 1 2 0 0 < < ij ij R R (21) where: ( ) ( ) 1 1 1 1 1 1 1 1 2 1 1 1 1 2 2 2 2 1 1 1 1 2 2 2 2 ˆ ˆ ˆsin sin cos ˆcos ˆ ˆsin sin − − − − − − − − − = + + + + + + = + + + + ϒ + ϒ + T T ij i i i j i j i j j T T i j j i i T T ij i i i j i j T T i i j j R A P PA N P PN B D P P B D B B R A P P A N P P N CP P C P D D P ρ θ ρ θ ρ θ ρ θ ε ρ θ ρ θ ε From the following variable changes 1=i iV D P , 2= ϒi iW P , by using Lemma (1) and using the Schur’s complement [39] to (21) results in (9) and (10). This completes the proof of the theorem. 4. ROBUST CONTROL OF THE FUZZY BILINEAR MODEL WITH UNCERTAINTIES In this section, we want to design the robust control of the FBM. The objective is to consider parametric uncertainties in the system for modelling the behaviour of complex nonlinear dynamic systems in order to design of a stabilizing control law, based on state estimation. The nonlinear system is modeled as a T-S fuzzy bilinear model. Then, the dynamic equation of the fuzzy bilinear system can be formulated in the following form: ( ) ( ) ( )1 ( ) ( ) ( ) ( ( )) ( ) ( ) ( ) ( ) =   + ∆ + + ∆ =    + + ∆    = ∑& r i i i i i i i i A A x t B B u t x t h t N N x t u t y t Cx t ξ (22) The parameter uncertainties considered here are norm-bounded and presented by the form [ ] [ ]1 2 3∆ ∆ ∆ =i i i i i i i iA B N M F E E E (23) where 1 2 3, , ,i i i iM E E E are known real constant matrices of appropriate dimensions, and iF is an unknown matrix function satisfying ( ) ( ) ≤T i iF t F t I , in which I is the identity matrix of appropriate dimension. The feedback controller and the state of fuzzy bilinear observer for T-S fuzzy bilinear model with parametric uncertainties (22) is the same as that for (2). In order to examine the robustness of the fuzzy controller (5), the augmented system is represented as follows: ( )ˆ( ) ( ) ( )=& a aX t A t X tξ (24) where the matrices ( )ˆ ( )A tξ and the augmented vector ( )aX t are respectively given by:
• 8.
  International Journal ofControl Theory and Computer Modeling (IJCTCM) Vol.6, No.1/2, April 2016 8 ( ) ( ) ( ) 1 1 ˆ ˆ( ) ( ) ( ) ( ) ( ) ( ) = = =   =     ∑∑ r r i j ij i j a A t h t h t A x t X t e t ξ ξ ξ with 11 12 21 22 ˆ Ξ Ξ  =  Ξ Ξ  ijA ( ) ( ) ( ) ( ) ( ) 11 12 21 22 ˆ ˆsin cos ˆcos ˆ ˆsin cos ˆ ˆsin cos Ξ = + ∆ + + ∆ + + ∆ Ξ = + ∆ Ξ = − ∆ + ∆ + ∆ Ξ = + + ϒ − ∆ i i i i j i i j j i i j j i i j i j j i i j i i j j A A N N B B D B B D A N B D A N C B D ρ θ ρ θ ρ θ ρ θ ρ θ ρ θ ρ θ The objective of this section is to seek a fuzzy observer-based controller of the form (5) such that the closed-loop fuzzy augmented system (24) is globally asymptotically stable. Therefore, we have a result that is summarized in the following theorem. Theorem 2: If there exist symmetric positive definite matrices 1P and 2P , matrices ,i iW V and positive scalars 0 , 0> >ε ρ such that LMIs (25) and (26) are satisfied, then the augmented system described by (24) is asymptotically stable 1 , 1∀ = ∀ =L Li r j r ( ) 1 1 1 2 3 1 1 1 2 2 1 1 * * * * * * * * * * * * * * * * * * * 0 * * * * * * * * 0 0 * * * * * * * 0 0 0 * * * * * * 0 0 0 0 * * * * * 0 0 0 0 0 * * * * 1 2 0 0 0 0 0 0 * * * 0 0 0 0 0 0 0 * * 0 0 0 0 0 0 0 0 * 0 0 0 0 0 0 0 0 0 − − − Π   −  −  −  −  −  −   + −   −  −  −  i i j i T i j i j T i i i j E P I E V I E P I M I V I E V I M I N P I BV I I I ε ε ε ρ ε ε ε ρ ε ρ 0        <         (25)
• 9.
  International Journal ofControl Theory and Computer Modeling (IJCTCM) Vol.6, No.1/2, April 2016 9 ( ) 2 1 2 3 2 2 1 2 2 1 2 2 * * * * * * * * * * * * * * * * * 0 * * * * * * * 0 0 * * * * * * 0 0 0 * * * * * 00 0 0 0 * * * * 0 0 0 0 0 * * * 1 2 0 0 0 0 0 0 * * 0 0 0 0 0 0 0 * 0 0 0 0 0 0 0 0 − − Π   −   −   −   −   <−   −    + −    −   −   i i j i T i T i i j T i i E I E D I E I B P I M P I E D I M P I P N I I I ε ε ε ρ ε ρ ε ε ρ ε ρ (26) where : 1 1 1 2 2 2,Π = + Π = + + +T T T T i i i i i iA P PA P A A P WC C W The gains of the observer and the state feedback control law are given by: 1 1 − =i iD V P (27) 1 2 − ϒ =i iP W (28) Proof: To prove the stability of the closed-loop for the augmented system (24), the sufficient conditions must be verified: ( )ˆ ˆ ˆˆ0 , , 0∃ = > = + <T D T ij ij ij ijQ Q M A Q A Q QA (29) Where 11 22 0 0   =     Q Q Q (30) Let us define ( ) 1 2ˆˆ ˆ ˆ, = +D D D ij ij ij ijM A Q M M (31) where 1 11 12 1 2 21 222 ˆ 0 ˆ ˆ, ˆ0    ∆ ∆ = =    ∆ ∆      ij ij ijD D ij ij ij ijij D M M D (32)
• 10.
  International Journal ofControl Theory and Computer Modeling (IJCTCM) Vol.6, No.1/2, April 2016 10 ( ) ( ) 1 11 11 11 11 11 11 2 22 22 22 22 22 22 11 11 11 11 11 11 ˆ ˆ ˆ ˆˆ sin sin cos cos ˆ ˆˆ sin sin ˆ ˆsin sin = + + + + + = + + + + ϒ + ϒ ∆ = ∆ + ∆ + ∆ + ∆ + ∆ TT T ij i i i j i j i j j i j j TT T ij i i i j i j i i T T ij i i i j i j D AQ Q A N Q Q N Q B D B D Q D AQ Q A N Q Q N CQ Q C AQ Q A N Q Q N Q B ρ θ ρ θ ρ θ ρ θ ρ θ ρ θ ρ θ ρ θ ρ ( ) ( ) ( ) ( ) 11 12 22 22 22 11 11 21 22 22 22 11 11 22 ˆ ˆcos cos ˆ ˆsin cos ˆ ˆcos cos ˆ ˆsin cos ˆ ˆcos cos + ∆ ∆ = − ∆ − ∆ − ∆ + ∆ + ∆ = −∆ − ∆ − ∆ + + ∆ ∆ T i j j i j j TT T ij i i j i j j i j j i j j ij i i j i j j T T i j j i j j ij D B D Q Q A Q N Q B D B D Q B D Q AQ N Q B D Q Q B D Q B D θ ρ θ ρ θ ρ θ ρ θ ρ θ ρ θ ρ θ ρ θ ρ θ ( )22 22 ˆ ˆcos cos= − ∆ − ∆ T i j j i j jB D Q Q B Dρ θ ρ θ (33) The equation 2ˆ D ijM can be reformulated as follows 2 1 2 3ˆ = Ψ + Ψ + ΨD ij ij ij ijM (34) with: 12 12 11 1 21 2 3 21 21 22 1 2 0 0 0 , , 0 0 0      Ψ Ψ ∆ Ψ = Ψ = Ψ =      Ψ Ψ ∆           ij ij ij ij ij ij ij ij ij (35) ( ) ( ) ( ) 12 1 22 22 22 21 1 22 22 22 12 2 11 11 21 2 11 11 ˆ ˆsin cos ˆ ˆsin cos ˆ ˆcos cos ˆ ˆ= cos cos Ψ = − ∆ − ∆ − ∆ Ψ = −∆ − ∆ − ∆ Ψ = ∆ + Ψ + ∆ TT T ij i i j i j j ij i i j i j j ij i j j i j j T T ij i j j i j j Q A Q N Q B D AQ N Q B D Q B D Q B D Q Q B D Q B D ρ θ ρ θ ρ θ ρ θ ρ θ ρ θ ρ θ ρ θ (36) Let 11 1=Q P and 1 22 2 − =Q P . Using the uncertainties structure and by using the separation Lemma (1) [40], one obtains: 1 2 2 ˆ 0 ˆ ˆ0   ≤      ijD ij ij T M T (37)
• 11.
  International Journal ofControl Theory and Computer Modeling (IJCTCM) Vol.6, No.1/2, April 2016 11 where: ( )1 2 1 1 1 2 2 1 1 2 1 1 1 1 1 1 1 2 2 1 1 1 3 3 1 2 1 1 1 1 1 1 1 1 1 2 1 1 2 2 3 3 2 2 2 2 2 ˆ 1 2 ˆ − − − − − − − − − − − − − = + + + + + + + = + + T T T T T ij i i i i j j j i i j T T T T T i i i i i i j i i j T i i T T T T ij i i i i j i i j T M F F M PD D P PD E E D P M F F M PE E P PD E E D P PE E P T P E E P P E E P P D E E D P ρ ε ε ε ε ρ ε ε ε ε ε ε ( )1 2 1 2 2 1 1 2 2 2 2 1 2− − − − + + + + + T T T T T i i i i i i i i i i T T j i i j B B M F F M M FF M P D E E D P ε ρ ε ρ ρ ε ε (38) From (31), (33) and (37), we have: ( ) 1 1 2 2 ˆ ˆ 0 ˆˆ , ˆ ˆ0  + ≤   +   ij ijD ij ij ij ij D T M A P D T (39) In order to verify (29), we must have: 1 2 ˆ 0 0 ˆ0   <     ij ij R R (40) where: 1 1 1 2 2 2 ˆ ˆ ˆ ˆ ˆ ˆ = + = + ij ij ij ij ij ij R D T R D T (41) Which implies : 1 2 ˆ 0 ˆ 0 < < ij ij R R (42) Using the following variable changes 1=i iV D P , 2= ϒi iW P , and using the Schur’s complement [39] to (42) results in (25) and (26). This completes the proof of the theorem. To illustrate the theoretical development and the design algorithm, numerical example is proposed in the following section. 5. SIMULATION EXAMPLE In this section, an example is given to illustrate the effectiveness of the proposed design conditions. Consider a nonlinear system represented by a T-S fuzzy bilinear model with uncertainties of two local models:
• 12.
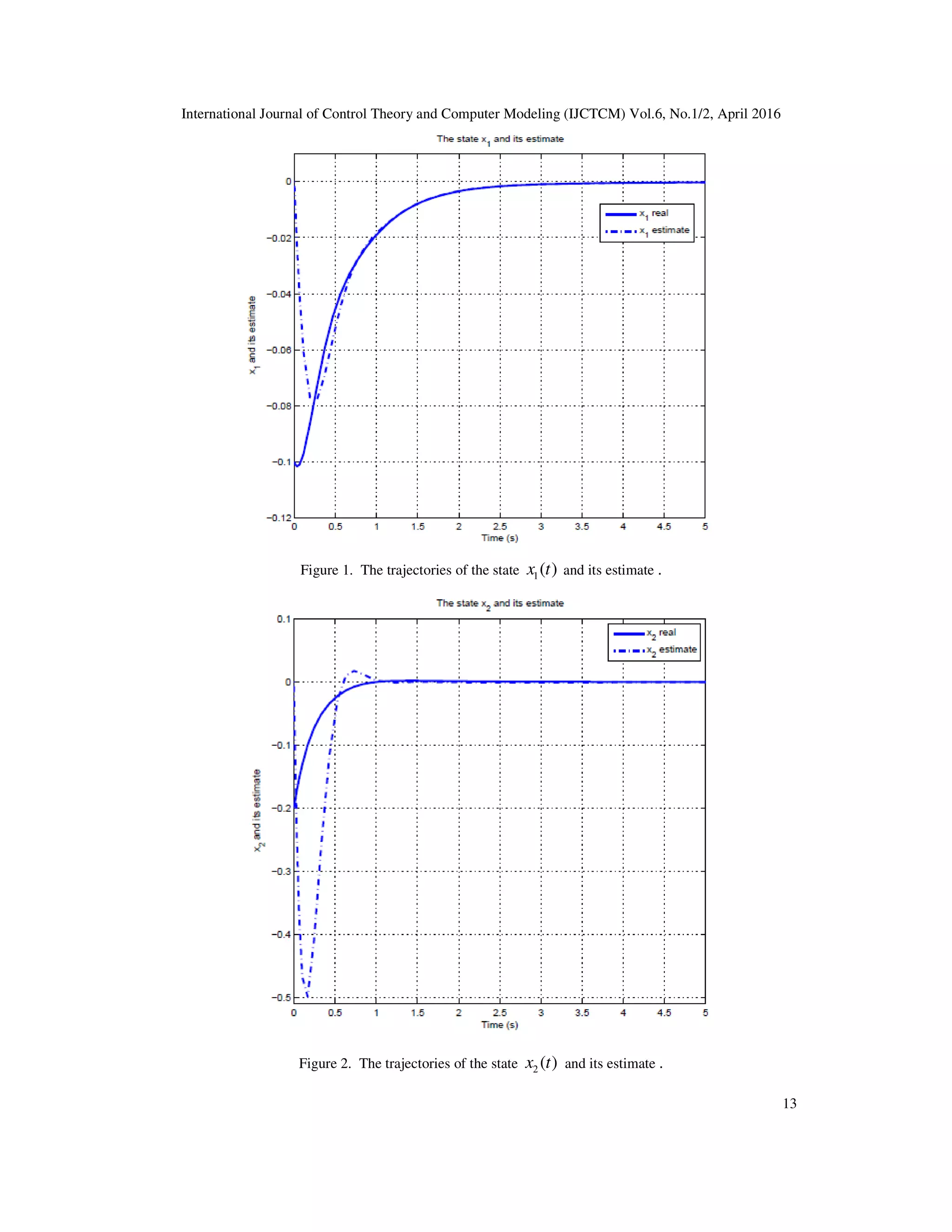
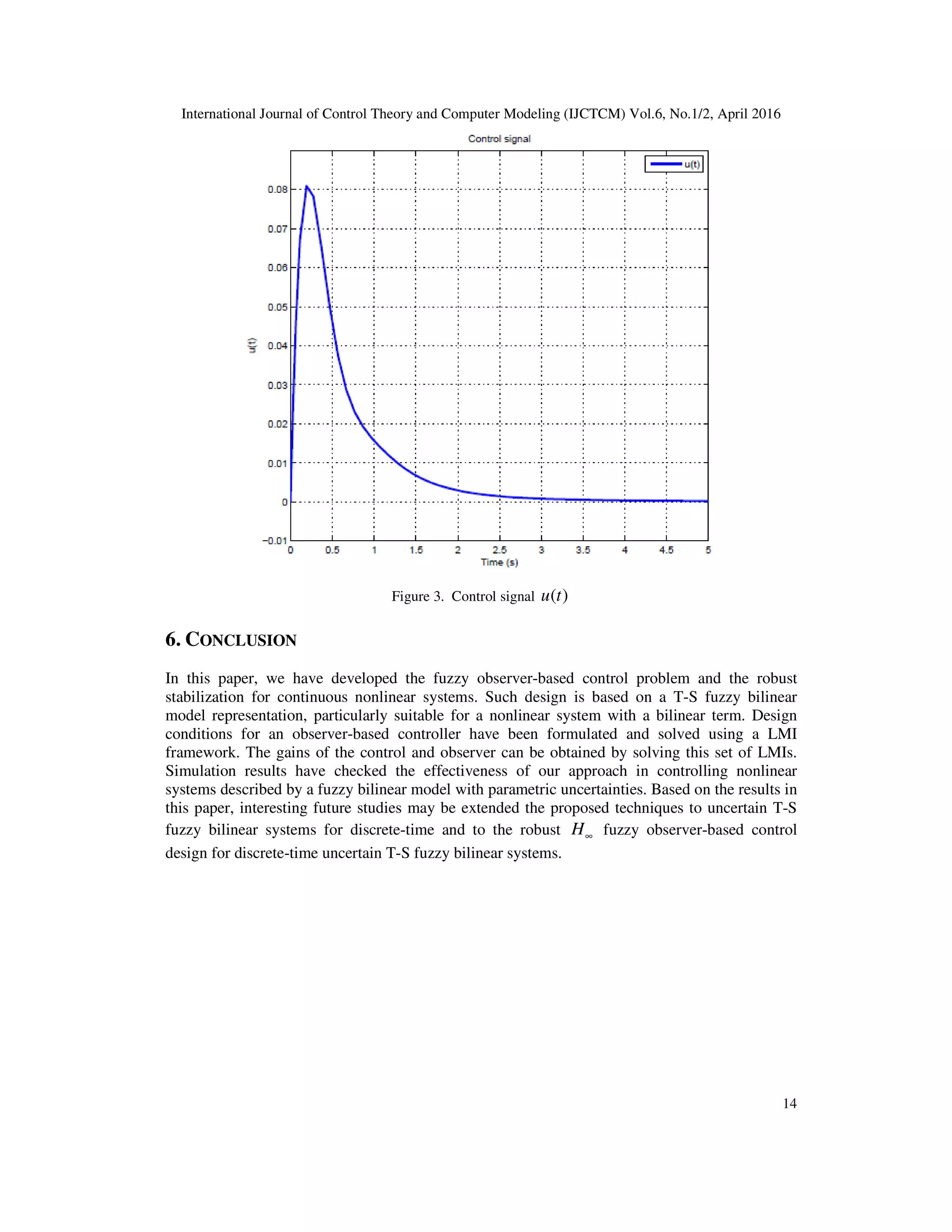
  International Journal ofControl Theory and Computer Modeling (IJCTCM) Vol.6, No.1/2, April 2016 12 ( ) ( ) ( ) 2 1 ( ) ( ) ( ) ( ( )) ( ) ( ) ( ) ( ) =   + ∆ + + ∆ =    + + ∆    = ∑& i i i i i i i i A A x t B B u t x t h t N N x t u t y t Cx t ξ The numerical values of those parameters are defined by: [ ] 1 1 1 2 2 2 0 0.8 1 1 0 , , 1.5 3.2 1 0 1 0 0.5 2 1 0 , , 1.5 3.4 1 0 1 1 0 −      = = =     − − − −      −      = = =     − − − −      = A B N A B N C Uncertainties are also defined by the following matrices: 1 11 21 31 2 12 22 32 0.1 0 0 0.5 1 0 0 , , , 0 0.1 0 0.3 0.5 0 0 0.1 0 0 0.5 1 0 0 , , , 0 0.1 0 0.6 0.5 0 0         = = = =                        = = = =                M E E E M E E E The weighting functions are defined by: ( ) ( ) ( ) 2 1 1 2 1 51( ) exp , ( ) 1 ( ) 2 2  +  = = −      x h x t h x t h x t In order to design robust observer-based controller for this uncertain T-S fuzzy bilinear system, we solve LMIs of theorem 2. So, we obtain the following controller and observer gain matrices respectively with 0.7=ρ : [ ] [ ] [ ] [ ] 2 2 1.94 0.18 , 1.35 0.08 , 7.74 80.83 , 7.79 82.25 = − − = − − ϒ = − − ϒ = − − i T T i D D The simulation results are shown in figures (1)-(3). Figures (1) and (2) show respectively the trajectories of states 1( )x t and 2 ( )x t of the considered system and their corresponding observer variables. One can see that the estimated states can closely track the original states despite of the presence of norm-bounded parametric uncertainties. Figure (3) shows the evolution of the control signal.
• 13.
  International Journal ofControl Theory and Computer Modeling (IJCTCM) Vol.6, No.1/2, April 2016 13 Figure 1. The trajectories of the state 1( )x t and its estimate . Figure 2. The trajectories of the state 2 ( )x t and its estimate .
• 14.
  International Journal ofControl Theory and Computer Modeling (IJCTCM) Vol.6, No.1/2, April 2016 14 Figure 3. Control signal ( )u t 6. CONCLUSION In this paper, we have developed the fuzzy observer-based control problem and the robust stabilization for continuous nonlinear systems. Such design is based on a T-S fuzzy bilinear model representation, particularly suitable for a nonlinear system with a bilinear term. Design conditions for an observer-based controller have been formulated and solved using a LMI framework. The gains of the control and observer can be obtained by solving this set of LMIs. Simulation results have checked the effectiveness of our approach in controlling nonlinear systems described by a fuzzy bilinear model with parametric uncertainties. Based on the results in this paper, interesting future studies may be extended the proposed techniques to uncertain T-S fuzzy bilinear systems for discrete-time and to the robust ∞H fuzzy observer-based control design for discrete-time uncertain T-S fuzzy bilinear systems.
• 15.
  International Journal ofControl Theory and Computer Modeling (IJCTCM) Vol.6, No.1/2, April 2016 15 REFERENCES [1] T. Takagi & M. Sugeno, (1985) “Fuzzy identification of systems and its applications to modeling and control”, IEEE Trans. Syst., Man, Cybern., Vol. SMC-15, no. 1, pp. 116-132. [2] K. Tanaka, T. Ikeda, and H. O. Wang, (1998) “Fuzzy regulators and fuzzy observers: Relaxed stability conditions and LMI-based designs”, IEEE Trans. Fuzzy syst., Vol. 6, no. 2, pp. 250-265. [3] K. Tanaka & H. O. Wang (2001) Fuzzy control systems design and analysis: a linear matrix inequality approach, New York: Wiley. [4] M. Chadli & T.-M. Guerra, (2012) “LMI solution for robust static output feedback control of Takagi- Sugeno fuzzy models”, IEEE Transaction on Fuzzy Systems, Vol. 20, no. 6, pp. 1160-1165. [5] E. Kim & H. Lee, (2000) “New approaches to relaxed quadratic stability condition of fuzzy control systems”, IEEE Transaction on Fuzzy Systems, Vol. 8, no. 5, pp. 523-534. [6] G. Feng & G. Chen, (2005) “Adaptive control of discrete-time chaotic systems: a fuzzy control approach”, Chaos, Solitons and Fractals, Vol. 23, no. 2, pp. 459-467. [7] B. Chen, X. P. Lin, , C. Lin, S. C. Tong, (2008) “Observer-based stabilization of T-S fuzzy systems with input delay”, IEEE Transaction on Fuzzy Systems, Vol. 16, no. 3, pp. 652-663. [8] S. K. Nguang & P. Shi, (2008) “ fuzzy output feedback control design for nonlinear systems: an LMI approach”, IEEE Transaction on Fuzzy Systems, Vol. 11, no. 3, pp. 331-340. [9] J. Yoneyama, M. Nishikawa, H. Katayama, A. Ichikawa, (2000) “Output stabilization of Takagi- Sugeno fuzzy systems”, IEEE Transaction on Fuzzy Systems, Vol. 111, no. 2, pp. 253-266. [10] C.-H. Fang, Y.-S. Liu, S.-W. Kau, L. Hong, C.-H. Lee, (2006) “A new LMI-based approach to relaxed quadratic stabilization of T-S fuzzy control systems”, IEEE Transaction on Fuzzy Systems, Vol. 14, no. 3, pp. 386-397. [11] T.M. Guerra & L. Vermeiren, (2004) “LMI-based relaxed nonquadratic stabilization conditions for nonlinear systems in the Takagi-Sugeno’s form”, Automatica, Vol. 40, no. 5, pp. 823-829. [12] K. Tanaka, T. Hori, H.O. Wang, (2003) “A multiple Lyapunov function approach to stabilization of fuzzy control systems”, IEEE Transaction on Fuzzy Systems, Vol. 11, no. 4, pp. 582-589. [13] H.-N. Wu & K.-Y. Cai, (2006) “ guaranteed cost fuzzy control design for discrete-time nonlinear systems with parameter uncertainty”, Automatica, Vol. 42, no. 7, pp. 1183-1188. [14] S. Zhou, G. Feng, J. Lam, S. Xu, (2005) “Robust control for discrete-time fuzzy systems via basis- dependent Lyapunov functions.”, Inf. Sci., Vol. 174, no. 3-4, pp. 197-217. [15] H.J. Lee, J.B. Park, G. Chen, (2001) “Robust fuzzy control of nonlinear systems with parametric uncertainties”, IEEE Transaction on Fuzzy Systems, Vol. 9, no. 2, pp. 369-379. [16] C.-S Tseng, B.-S Chen and Y.-F Li, (2009) “Robust fuzzy observer-based fuzzy control design for nonlinear systems with persistent bounded disturbances: A novel decoupled approach”, Fuzzy Sets Syst., Vol. 160, no. 19, pp. 2824-2843. [17] J.-C. Lo & M.-L. Lin, (2004) “Observer-based robust control for fuzzy systems using two-step procedure”, IEEE Transaction on Fuzzy Systems, Vol. 12, no. 3, pp. 350-359. [18] X. Liu & Q. Zhang, (2003) “New approaches to controller designs based on fuzzy observers for T-S fuzzy systems via LMI”, Automatica, Vol. 39, no. 9, pp. 1571-1582. [19] B. Mansouri, N. Manamanni, K. Guelton, A. Kruszewski and T.M. Guerra, (2009) “Output feedback LMI tracking control conditions with criterion for uncertain and disturbed T-S models”, Information Sciences, Vol. 179, no. 4, pp. 446-457. [20] J. Yoneyama, (2006) “Robust control analysis and synthesis for Takagi-Sugeno general uncertain fuzzy systems: A novel decoupled approach”, Fuzzy Sets Syst., Vol. 157, no. 16, pp. 2205-2223. [21] S. Tong & H.-X. Li, (2002) “Observer-based robust fuzzy control of nonlinear systems with parametric uncertainties”, Fuzzy Sets Syst., Vol. 131, no. 2, pp. 165-184. [22] T.-H.S. Li & S.-H. Tsai, (2007) “T-S Fuzzy Bilinear Model and Fuzzy Controller Design for a Class of Nonlinear Systems”, IEEE Trans. Fuzzy Syst., Vol. 15, no. 3, pp. 494-506. [23] T.-H.S. Li & S.-H. Tsai, (2008) “Robust fuzzy control for a class of uncertain discrete fuzzy bilinear systems”, IEEE Trans. on system, Man, and Cybernetics, Vol. 38, no. 2, pp. 510-526. [24] S.-H. Tsai & T.-H.S. Li, (2009) “Robust fuzzy control of a class of fuzzy bilinear systems with time- delay”, Chaos, Solitons Fractals, Vol. 39, no. 15, pp. 2028-2040. [25] G. Zhang & M. Song, (2010) “Static output feedback control for discrete-time fuzzy bilinear system”, J. Syst. Eng. Electron, Vol. 21, no. 2, pp. 296-299.
• 16.
  International Journal ofControl Theory and Computer Modeling (IJCTCM) Vol.6, No.1/2, April 2016 16 [26] S.-H. Tsai, (2011) “Robust control for Van de Vusse reactor via T-S fuzzy bilinear scheme”, Expert Systems with Applications, Vol. 38, no. 5, pp. 4935-4944. [27] R. Takada, Y. Uchida and J. Yoneyama, (2013) “Output feedback control design with guaranteed cost for fuzzy bilinear time-delay systems”, Applied Mathematical Sciences, Vol. 7, no. 27, pp. 1303- 1318. [28] T.-H.S. Li, S.-H. Tsai, and M.-Y. Hsiao, (2009) “Robust fuzzy control for a class of time-delay fuzzy bilinear systems with an additive disturbance”, Int. J. Nonlinear Sci. Numerical Simul., Vol. 10, no. 3, pp. 315-322. [29] D. Saoudi , M. Chadli and N. B. Braiek (2015) Robust Estimation Design for Unknown Inputs Fuzzy Bilinear Models: Application to Faults diagnosis, Springer book: Complex system modelling and control through intelligent soft computations studies in fuzziness and soft computing, Vol. 319, pp. 655-685. [30] D. Saoudi , M. Chadli and N. B. Braiek, (2014) “Robust fault detection for fuzzy bilinear systems via unknown input observer”, In Proc. 22th Medit. Conf. Contr. Aut., pp. 281-286. [31] D. Saoudi , M. Chadli and N. B. Braiek, (2013) “State Estimation for Unknown Input Fuzzy Bilinear Systems: Application to Fault Diagnosis”, European Control Conference ECC, pp. 2465-2470. [32] D. Saoudi , M. Chadli C. Mechmeche and N. B. Braiek, (2012) “Unknown Input Observer Design for Fuzzy Bilinear System: an LMI Approach”, J. of Mathematical Problems in Engineering MPE, pp. 1- 21. [33] J. Baek & M. Park, (2012) “Fuzzy bilinear state feedback control design based on T-S fuzzy bilinear model for DC-DC converters”, Electrical Power and Energy Systems, Vol. 42, no. 1, pp. 710-720. [34] S.-H. Tsai, (2012) “A Global Exponential Fuzzy Observer Design for time-Delay Takagi–Sugeno Uncertain Discrete Fuzzy Bilinear Systems with Disturbance”, IEEE Trans. Fuzzy Syst., Vol. 20, no. 6, pp. 1063-1075. [35] D. Saoudi, M. Chadli and N. B. Braeik, (2015) “Fault Tolerant Control for Uncertain Fuzzy Bilinear Models”, Proc. of the IFAC Safeprocess'15, Vol. 48, no. 21, pp. 1256-1261. [36] D. Saoudi, C. Mechmeche, M. Chadli and N. B. Braeik, (2012) “Robust residual generator design for Takagi-Sugeno fuzzy bilinear system subject to unknown inputs”, Proc. of the IFAC Safeprocess'12, pp. 1023-1028. [37] D. Saoudi, M. Chadli and N. B. Braeik, (2014) “Fault Tolerant Control for Nonlinear Systems Described by Fuzzy Bilinear Models”, International Conference on Electrical Engineering and Control Applications ICEECA, pp. 1-6. [38] J.-S. Chiou, F.-C. Kung, T.-H.S. Li, (2000) “Robust stabilization of a class of singularly perturbed discrete bilinear systems”, IEEE Transactions on Automatic Control, Vol. 45, no. 6, pp. 1187-1191. [39] S. Boyd, L. El Ghaoui, E. Feron, V. Balakrishnan, (1994) Linear Matrix Inequalities in System and Control Theory, SIAM, Society for Industrial and Applied Mathematics, University City Science Center, Philadelphia, Pennsylvania. [40] G. Shi, Y. Zou, C. Yang, (1992) “An algebraic approach to robust control via state feedback”, System Control Letters, Vol. 18, no. 5, pp. 365-370.