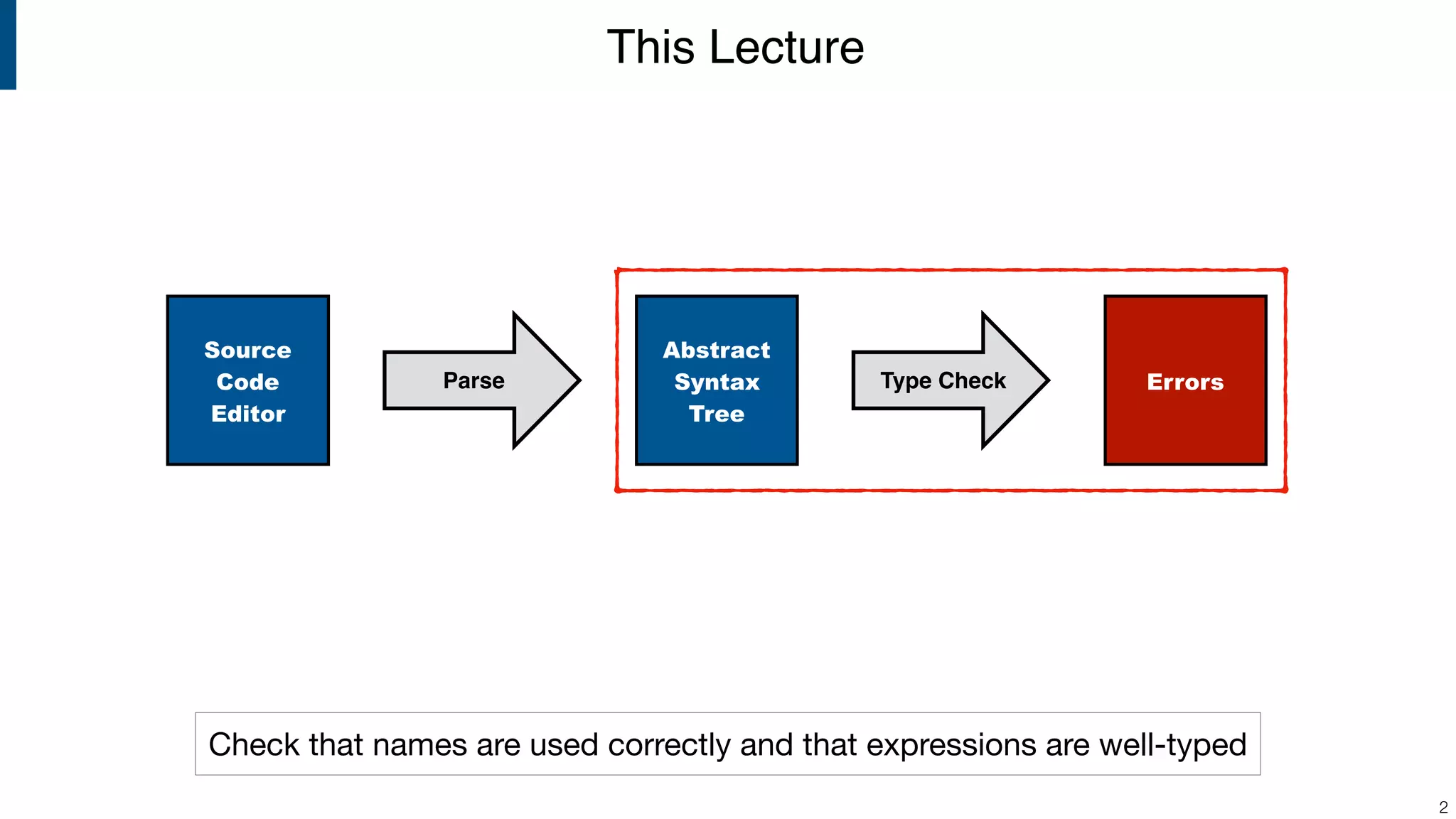
The lecture by Eelco Visser discusses static analysis in compiler construction, focusing on type checking and name binding in programming languages. It introduces concepts such as constraint-based type checkers, scope graphs, and the upcoming Statix DSL for defining type systems. The document also compares static and dynamic type checking while providing examples of syntax definitions and issues related to context-sensitive properties.










![Syntax of Book Catalogues !13 context-free syntax Document.Catalogue = [ <catalogue> [Book*] </catalogue> ] Book.Book = [ <book> [Title] [Author] [Publisher] </book> ] …Schema-specific syntax definition <catalogue> <book> <title>Modern Compiler Implementation in ML</title> <author>Andrew Appel</author> <publisher>Cambridge</publisher> </book> <book> <title>Parsing Schemata</title> <author>Klaas Sikkel</author> <publisher>Springer</publisher> </book> </catalogue>](https://image.slidesharecdn.com/cs4200-2018-6-intro-to-static-analysis-181002210659/75/Compiler-Construction-Lecture-6-Introduction-to-Static-Analysis-13-2048.jpg)
![A Generic Syntax of XML Documents !14 context-free start-symbols Document sorts Tag Word lexical syntax Tag = [a-zA-Z][a-zA-Z0-9]* Word = ~[<>]+ lexical restrictions Word -/- ~[<>] sorts Document Elem context-free syntax Document.Doc = Elem Elem.Node = [ <[Tag]> [Elem*] </[Tag]> ] Elem.Text = Word+ {longest-match} <catalogue> <book> <title>Modern Compiler Implementation in ML</title> <author>Andrew Appel</author> <publisher>Cambridge</publisher> </book> <book> <title>Parsing Schemata</title> <author>Klaas Sikkel</author> <publisher>Springer</publisher> </book> </catalogue> Doc( Node( "catalogue" , [ Node( "book" , [ Node("title", [Text(["Modern Compiler Implementation in ML"])], "title") , Node("author", [Text(["Andrew Appel"])], "author") , Node("publisher", [Text(["Cambridge"])], "publisher") ] , "book" ) , Node( "book" , [ Node("title", [Text(["Parsing Schemata"])], "title") , Node("author", [Text(["Klaas Sikkel"])], "author") , Node("publisher", [Text(["Springer"])], "publisher") ] , "book" ) ] , "catalogue" ) )](https://image.slidesharecdn.com/cs4200-2018-6-intro-to-static-analysis-181002210659/75/Compiler-Construction-Lecture-6-Introduction-to-Static-Analysis-14-2048.jpg)
![A Generic Syntax of XML Documents !15 context-free start-symbols Document sorts Tag Word lexical syntax Tag = [a-zA-Z][a-zA-Z0-9]* Word = ~[<>]+ lexical restrictions Word -/- ~[<>] sorts Document Elem context-free syntax Document.Doc = Elem Elem.Node = [ <[Tag]> [Elem*] </[Tag]> ] Elem.Text = Word+ {longest-match} <catalogue> <book> <title>Modern Compiler Implementation in ML</title> <author>Andrew Appel</author> <publisher>Cambridge</publisher> </book> <book> <title>Parsing Schemata</title> <author>Klaas Sikkel</author> <publisher>Springer</publisher> </book> </catalogue> What is the problem with this approach?](https://image.slidesharecdn.com/cs4200-2018-6-intro-to-static-analysis-181002210659/75/Compiler-Construction-Lecture-6-Introduction-to-Static-Analysis-15-2048.jpg)
![Generic Syntax is Too Liberal! !16 context-free start-symbols Document sorts Tag Word lexical syntax Tag = [a-zA-Z][a-zA-Z0-9]* Word = ~[<>]+ lexical restrictions Word -/- ~[<>] sorts Document Elem context-free syntax Document.Doc = Elem Elem.Node = [ <[Tag]> [Elem*] </[Tag]> ] Elem.Text = Word+ {longest-match} <catalogue> <book> <title>Modern Compiler Implementation in ML</title> <author>Andrew Appel</author> <publisher>Cambridge</publisher> <year></year> </book> <language> <name>SDF3</name> <purpose>Syntax Definition</purpose> <implementedin>SDF3</implementedin> </language> <book> //<title>Parsing Schemata</title> <author>Klaas Sikkel</author> <publisher>Springer</publisher> </book> <book> </koob> </catalogue> Year is not a valid element of book Only books in catalogue Book should have a title Closing tag is not consistent with starting tag](https://image.slidesharecdn.com/cs4200-2018-6-intro-to-static-analysis-181002210659/75/Compiler-Construction-Lecture-6-Introduction-to-Static-Analysis-16-2048.jpg)



![Doc( Node( "catalogue" , [ Node( "book" , [ Node("title", [Text(["Modern Compiler Implementation in ML"])], "title") , Node("author", [Text(["Andrew Appel"])], "author") , Node("publisher", [Text(["Cambridge"])], "publisher") , Node("year", [], "year") ] , "book" ) , Node( "language" , [ Node("name", [Text(["SDF3"])], "name") , Node("purpose", [Text(["Syntax Definition"])], "purpose") , Node("implementedin", [Text(["SDF3"])], "implementedin") ] , "language" ) , Node( "book" , [ Node("author", [Text(["Klaas Sikkel"])], "author") , Node("publisher", [Text(["Springer"])], "publisher") ] , "book" ) , Node("book", [], "koob") ] , "catalogue" ) ) Checking Context-Context-Sensitive Properties in Spoofax !20 rules // Analysis editor-analyze: (ast, path, project-path) -> (ast', error*, warning*, info*) with ast' := <id> ast ; error* := <collect-all(constraint-error)> ast' ; warning* := <collect-all(constraint-warning)> ast' ; info* := <collect-all(constraint-info)> ast' parse errors](https://image.slidesharecdn.com/cs4200-2018-6-intro-to-static-analysis-181002210659/75/Compiler-Construction-Lecture-6-Introduction-to-Static-Analysis-20-2048.jpg)

![Check Violations using Constraint-Error Rules !22 <catalogue> <book> <title>Modern Compiler Implementation in ML</title> <author>Andrew Appel</author> <publisher>Cambridge</publisher> <year></year> </book> <language> <name>SDF3</name> <purpose>Syntax Definition</purpose> <implementedin>SDF3</implementedin> </language> <book> //<title>Parsing Schemata</title> <author>Klaas Sikkel</author> <publisher>Springer</publisher> </book> <book> </koob> </catalogue> Closing tag does not match starting tag rules constraint-error : Node(tag1, elems, tag2) -> (tag2, $[Closing tag does not match starting tag]) where <not(eq)>(tag1, tag2) Origin Error message](https://image.slidesharecdn.com/cs4200-2018-6-intro-to-static-analysis-181002210659/75/Compiler-Construction-Lecture-6-Introduction-to-Static-Analysis-22-2048.jpg)
![Check Violations using Constraint-Error Rules !23 <catalogue> <book> <title>Modern Compiler Implementation in ML</title> <author>Andrew Appel</author> <publisher>Cambridge</publisher> <year></year> </book> <language> <name>SDF3</name> <purpose>Syntax Definition</purpose> <implementedin>SDF3</implementedin> </language> <book> //<title>Parsing Schemata</title> <author>Klaas Sikkel</author> <publisher>Springer</publisher> </book> <book> </koob> </catalogue> Book should have a title rules constraint-error : n@Node(tag@"book", elems, _) -> (tag, $[Book should have title]) where <not(has(|"title"))> elems has(|tag) = fetch(?Node(tag, _, _)) Containment checks](https://image.slidesharecdn.com/cs4200-2018-6-intro-to-static-analysis-181002210659/75/Compiler-Construction-Lecture-6-Introduction-to-Static-Analysis-23-2048.jpg)
![Check Violations using Constraint-Error Rules !24 <catalogue> <book> <title>Modern Compiler Implementation in ML</title> <author>Andrew Appel</author> <publisher>Cambridge</publisher> <year></year> </book> <language> <name>SDF3</name> <purpose>Syntax Definition</purpose> <implementedin>SDF3</implementedin> </language> <book> //<title>Parsing Schemata</title> <author>Klaas Sikkel</author> <publisher>Springer</publisher> </book> <book> </koob> </catalogue> Catalogue can only have books rules constraint-error : Node("catalogue", elems, _) -> error where <filter(not-a-book)> elems => [error | _] not-a-book : Node(tag, _, _) -> (tag, $[Catalogue can only have books]) where <not(eq)> (tag, "book") Containment checks](https://image.slidesharecdn.com/cs4200-2018-6-intro-to-static-analysis-181002210659/75/Compiler-Construction-Lecture-6-Introduction-to-Static-Analysis-24-2048.jpg)
![Check Violations using Constraint-Error Rules !25 <catalogue> <book> <title>Modern Compiler Implementation in ML</title> <author>Andrew Appel</author> <publisher>Cambridge</publisher> <year></year> </book> <language> <name>SDF3</name> <purpose>Syntax Definition</purpose> <implementedin>SDF3</implementedin> </language> <book> //<title>Parsing Schemata</title> <author>Klaas Sikkel</author> <publisher>Springer</publisher> </book> <book> </koob> </catalogue> Book can only have title, author, publisher rules constraint-error : Node("book", elems, _) -> error where <filter(not-a-book-elem)> elems => [error | _] not-a-book-elem : Node(tag, _, _) -> (tag, $[Book can only have title, author, publisher]) where <not(elem())> (tag, ["title", "author", "publisher"]) Containment checks](https://image.slidesharecdn.com/cs4200-2018-6-intro-to-static-analysis-181002210659/75/Compiler-Construction-Lecture-6-Introduction-to-Static-Analysis-25-2048.jpg)
















![Testing Name Resolution !43 test inner name [[ let type t = u type u = int var x: u := 0 in x := 42 ; let type [[u]] = t var y: [[u]] := 0 in y := 42 end end ]] resolve #2 to #1 test outer name [[ let type t = u type [[u]] = int var x: [[u]] := 0 in x := 42 ; let type u = t var y: u := 0 in y := 42 end end ]] resolve #2 to #1](https://image.slidesharecdn.com/cs4200-2018-6-intro-to-static-analysis-181002210659/75/Compiler-Construction-Lecture-6-Introduction-to-Static-Analysis-43-2048.jpg)
![Testing Type Checking !44 test variable reference [[ let type t = u type u = int var x: u := 0 in x := 42 ; let type u = t var y: u := 0 in y := [[x]] end end ]] run get-type to INT() test integer constant [[ let type t = u type u = int var x: u := 0 in x := 42 ; let type u = t var y: u := 0 in y := [[42]] end end ]] run get-type to INT()](https://image.slidesharecdn.com/cs4200-2018-6-intro-to-static-analysis-181002210659/75/Compiler-Construction-Lecture-6-Introduction-to-Static-Analysis-44-2048.jpg)
![Testing Errors !45 test undefined variable [[ let type t = u type u = int var x: u := 0 in x := 42 ; let type u = t var y: u := 0 in y := [[z]] end end ]] 1 error test type error [[ let type t = u type u = string var x: u := 0 in x := 42 ; let type u = t var y: u := 0 in y := [[x]] end end ]] 1 error](https://image.slidesharecdn.com/cs4200-2018-6-intro-to-static-analysis-181002210659/75/Compiler-Construction-Lecture-6-Introduction-to-Static-Analysis-45-2048.jpg)

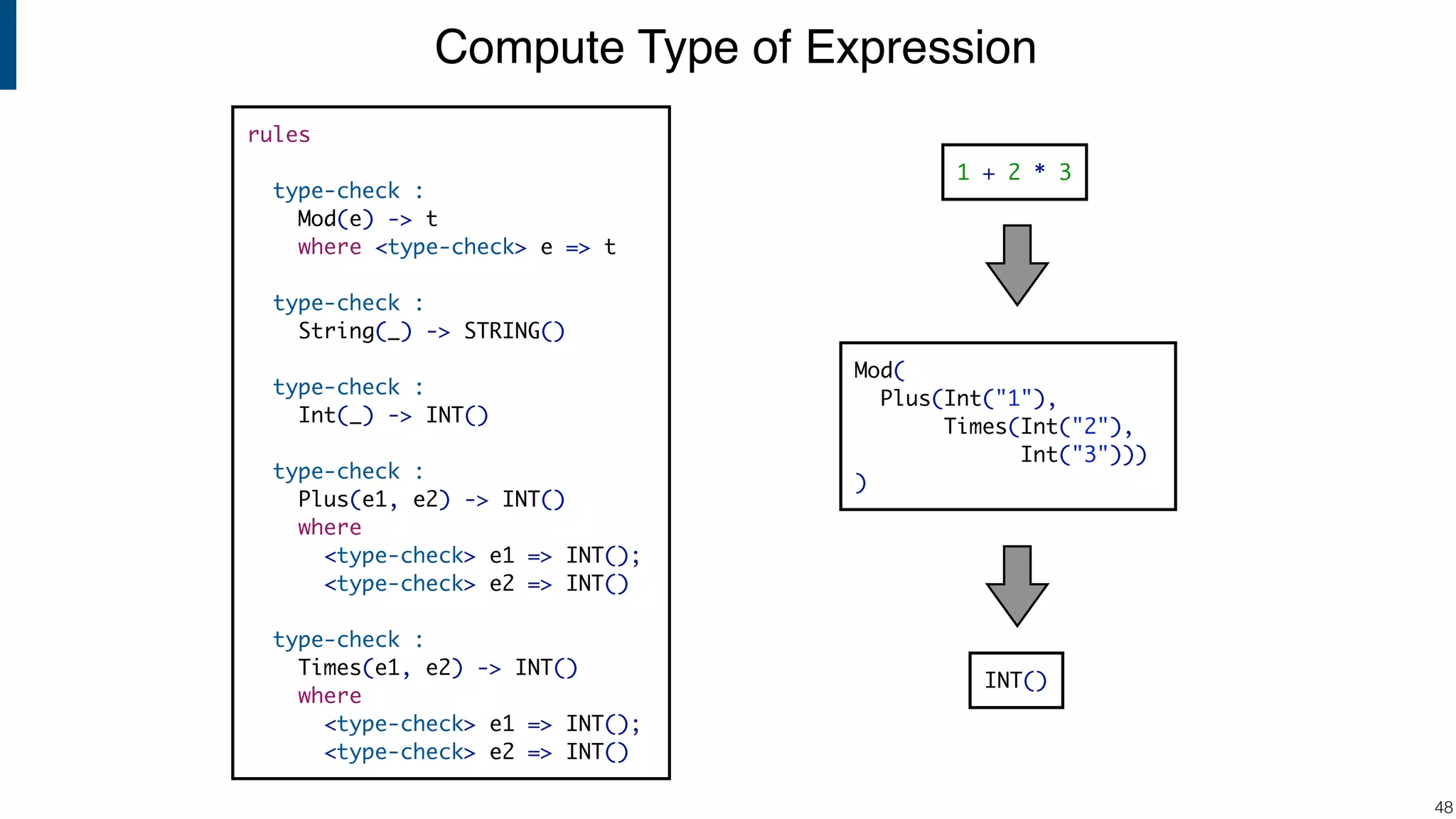
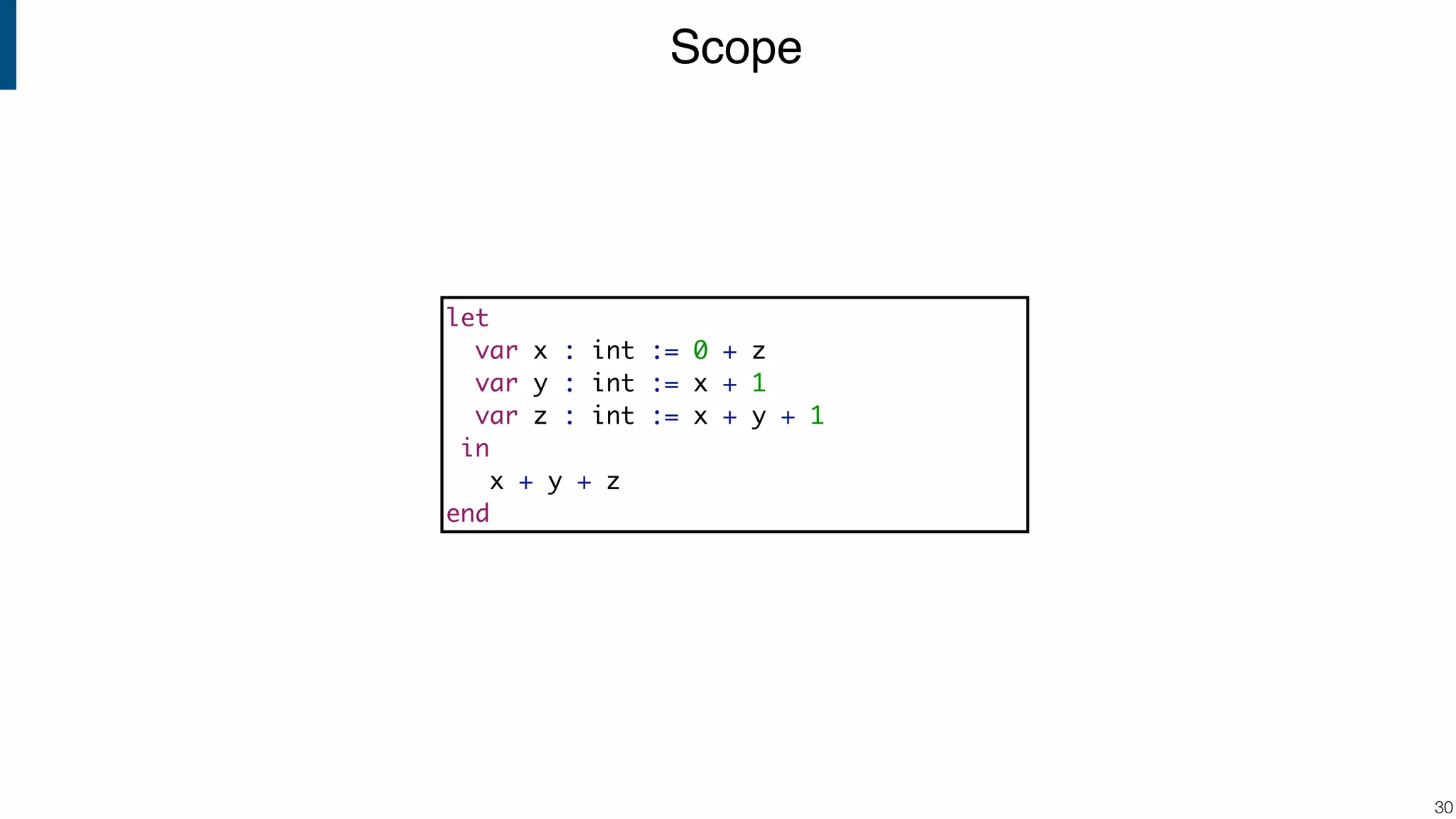
![Compute Type of Variable? !49 rules type-check : Let([VarDec(x, e)], e_body) -> t where <type-check> e => t_e; <type-check> e_body => t type-check : Var(x) -> t // ??? let var x := 1 in x + 1 end Mod( Let( [VarDec("x", Int("1"))] , [Plus(Var("x"), Int("1"))] ) ) ?](https://image.slidesharecdn.com/cs4200-2018-6-intro-to-static-analysis-181002210659/75/Compiler-Construction-Lecture-6-Introduction-to-Static-Analysis-49-2048.jpg)
![Type Checking Variable Bindings !50 rules type-check(|env) : Let([VarDec(x, e)], e_body) -> t where <type-check(|env)> e => t_e; <type-check(|[(x, t_e) | env])> e_body => t type-check(|env) : Var(x) -> t where <fetch(?(x, t))> env let var x := 1 in x + 1 end INT()Store association between variable and type in type environment Mod( Let( [VarDec("x", Int("1"))] , [Plus(Var("x"), Int("1"))] ) )](https://image.slidesharecdn.com/cs4200-2018-6-intro-to-static-analysis-181002210659/75/Compiler-Construction-Lecture-6-Introduction-to-Static-Analysis-50-2048.jpg)
![Pass Environment to Sub-Expressions !51 rules type-check : Mod(e) -> t where <type-check(|[])> e => t type-check(|env) : String(_) -> STRING() type-check(|env) : Int(_) -> INT() type-check(|env) : Plus(e1, e2) -> INT() where <type-check(|env)> e1 => INT(); <type-check(|env)> e2 => INT() type-check(|env) : Times(e1, e2) -> INT() where <type-check(|env)> e1 => INT(); <type-check(|env)> e2 => INT() let var x := 1 in x + 1 end INT() Mod( Let( [VarDec("x", Int("1"))] , [Plus(Var("x"), Int("1"))] ) )](https://image.slidesharecdn.com/cs4200-2018-6-intro-to-static-analysis-181002210659/75/Compiler-Construction-Lecture-6-Introduction-to-Static-Analysis-51-2048.jpg)



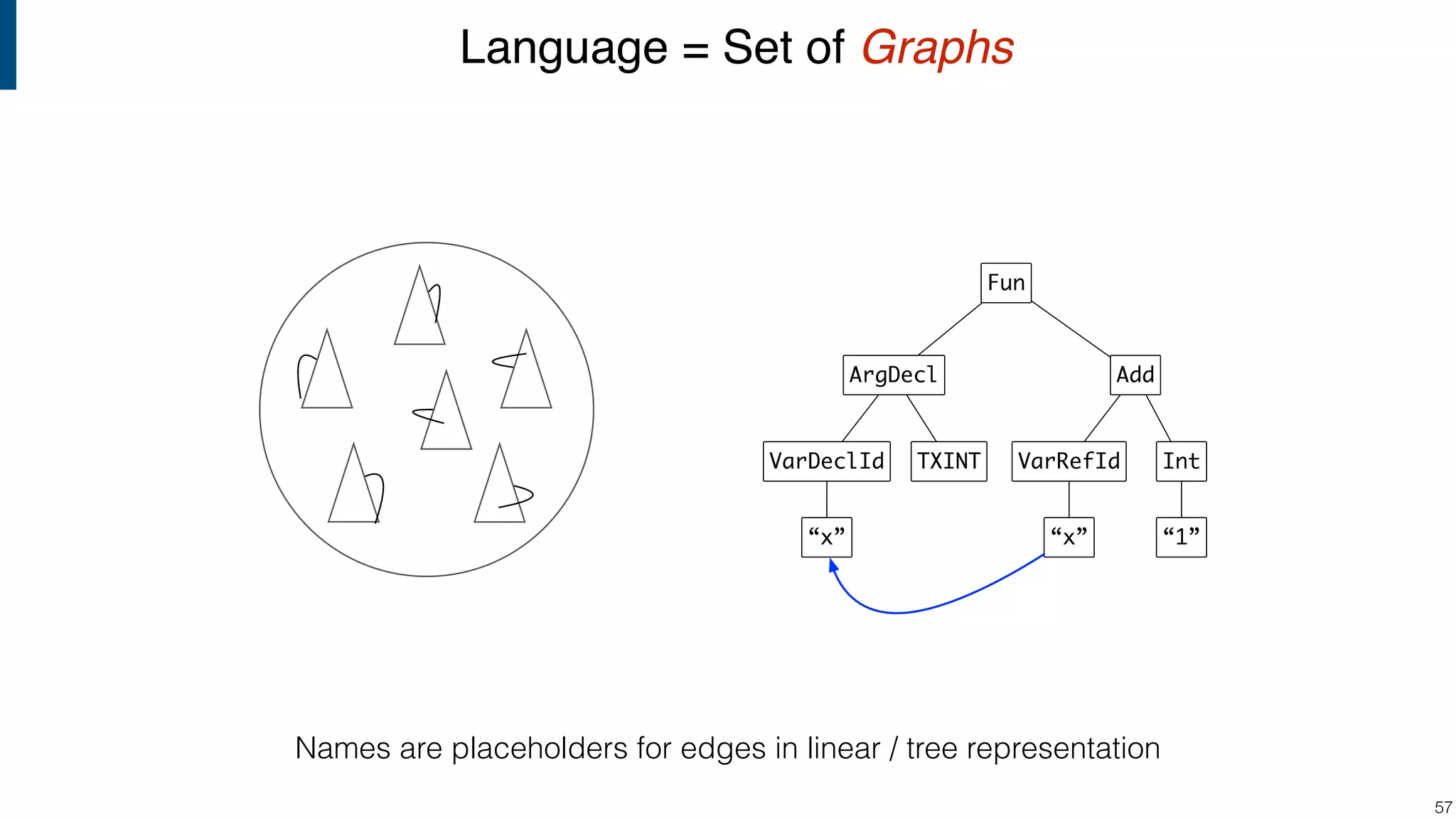














![DSLs for specifying binding structure of a (target) language - Ott [Sewell+10] - Romeo [StansiferWand14] - Unbound [Weirich+11] - Cαml [Pottier06] - NaBL [Konat+12] Generate code to do resolution and record results What is the semantics of such a name binding language? !72 Name Binding Languages](https://image.slidesharecdn.com/cs4200-2018-6-intro-to-static-analysis-181002210659/75/Compiler-Construction-Lecture-6-Introduction-to-Static-Analysis-72-2048.jpg)





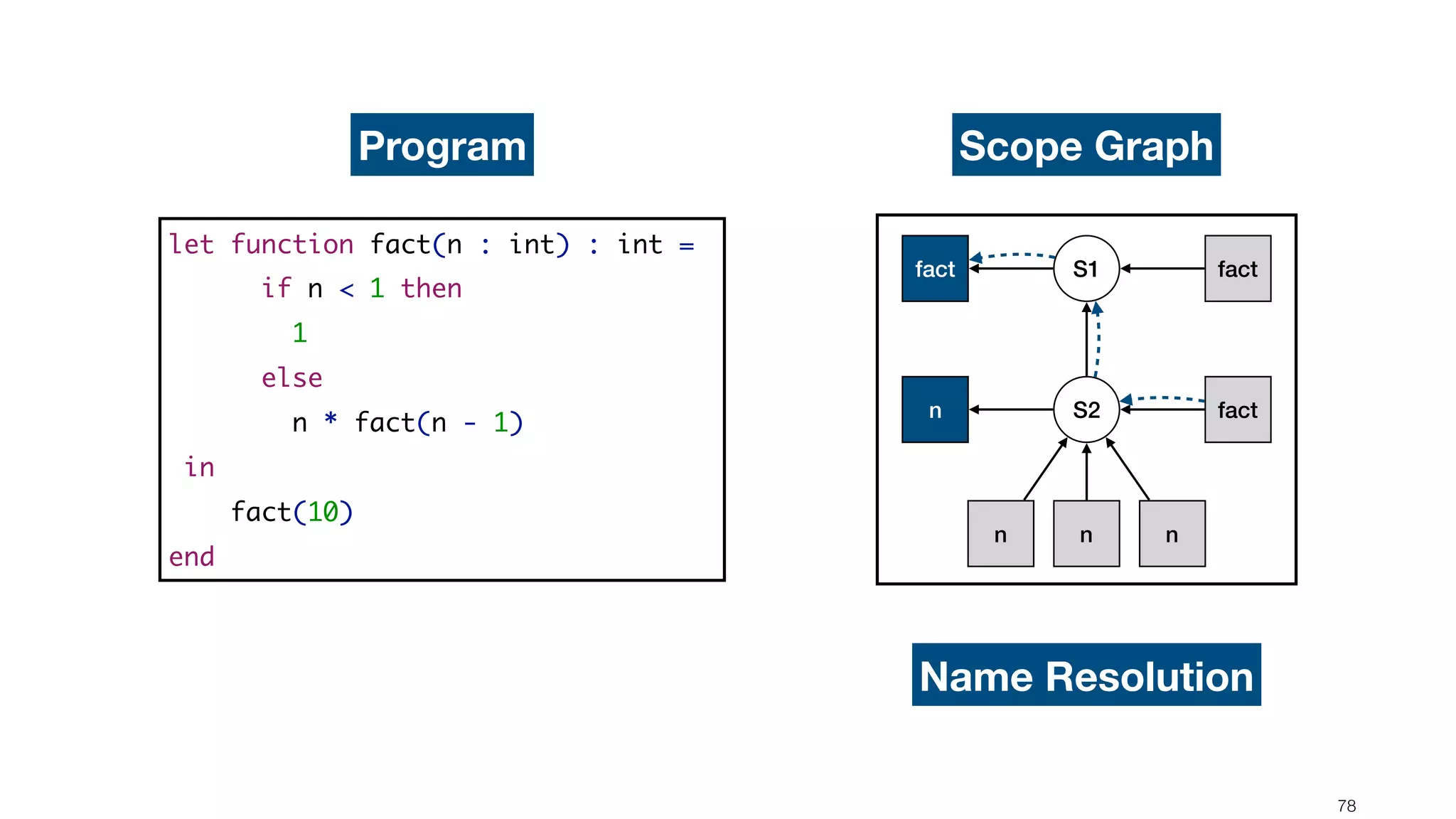
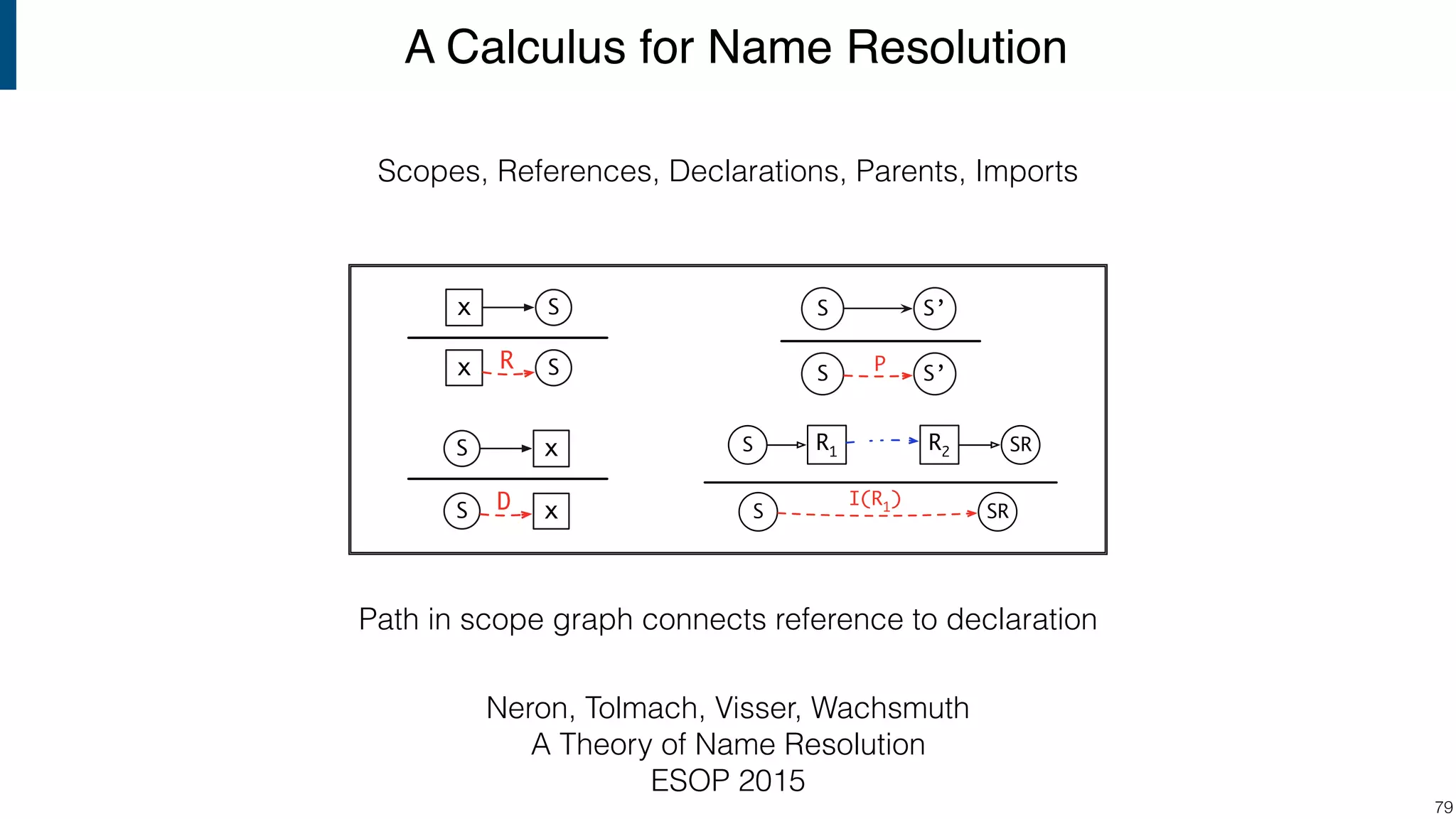
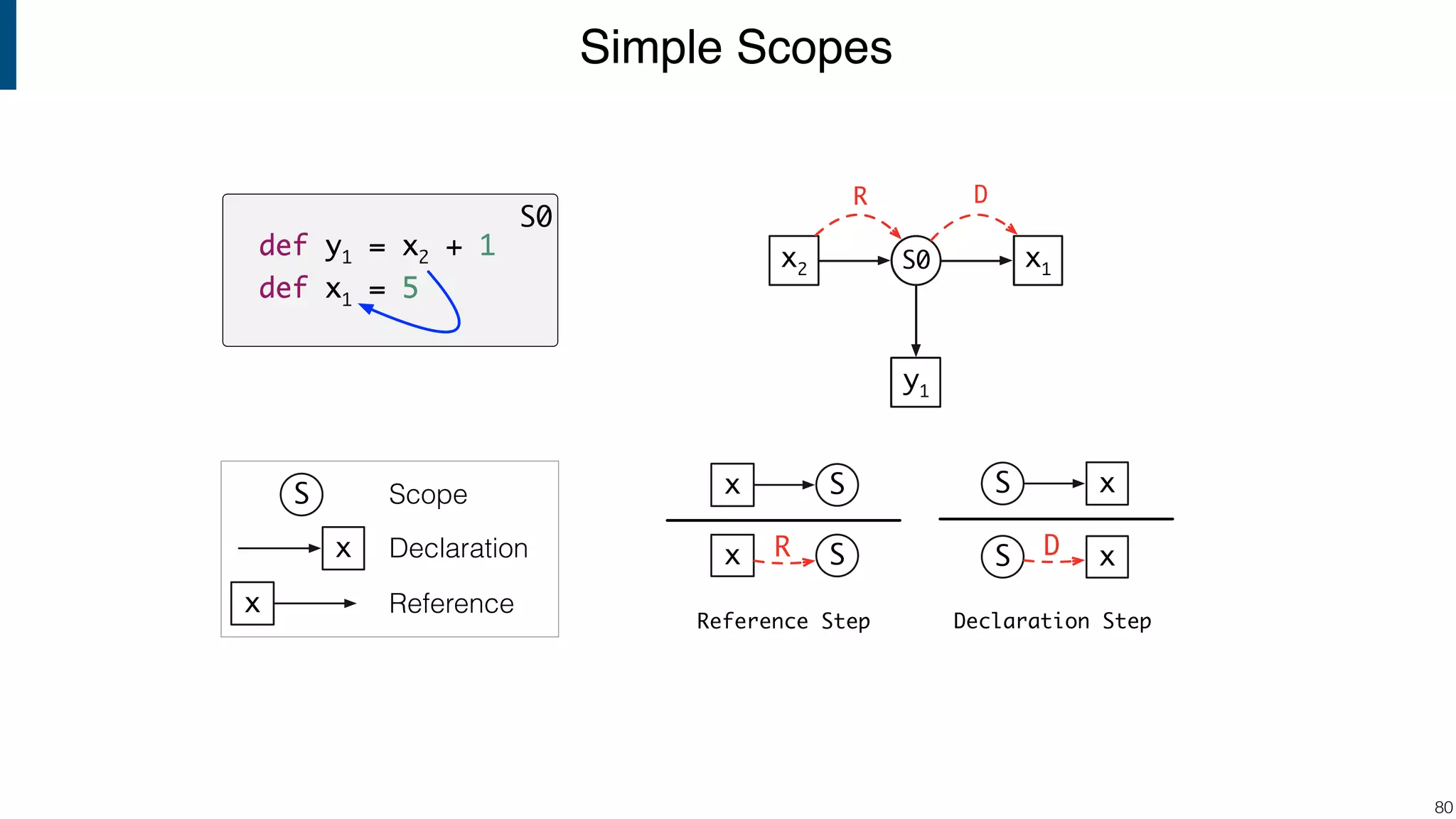
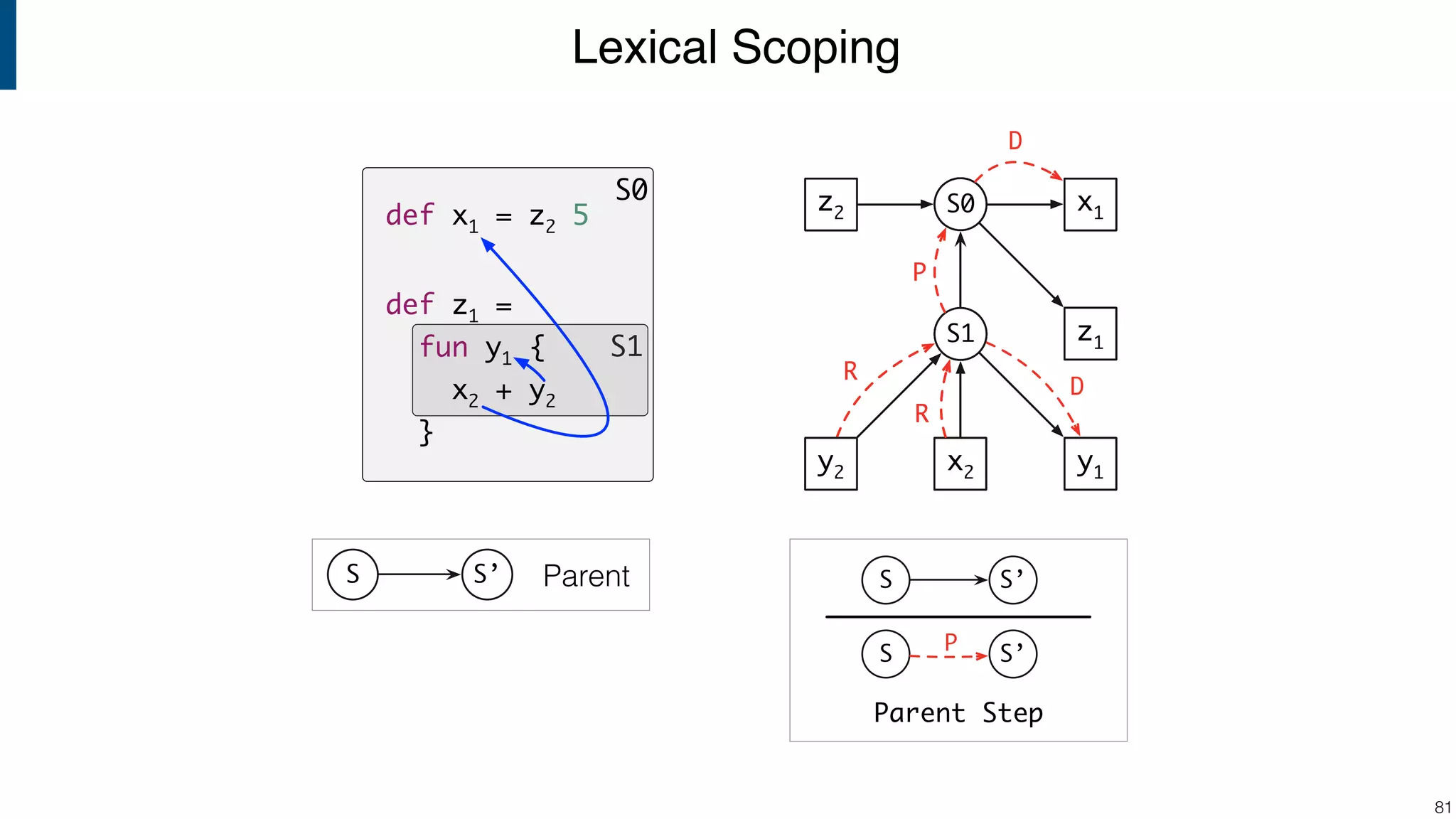
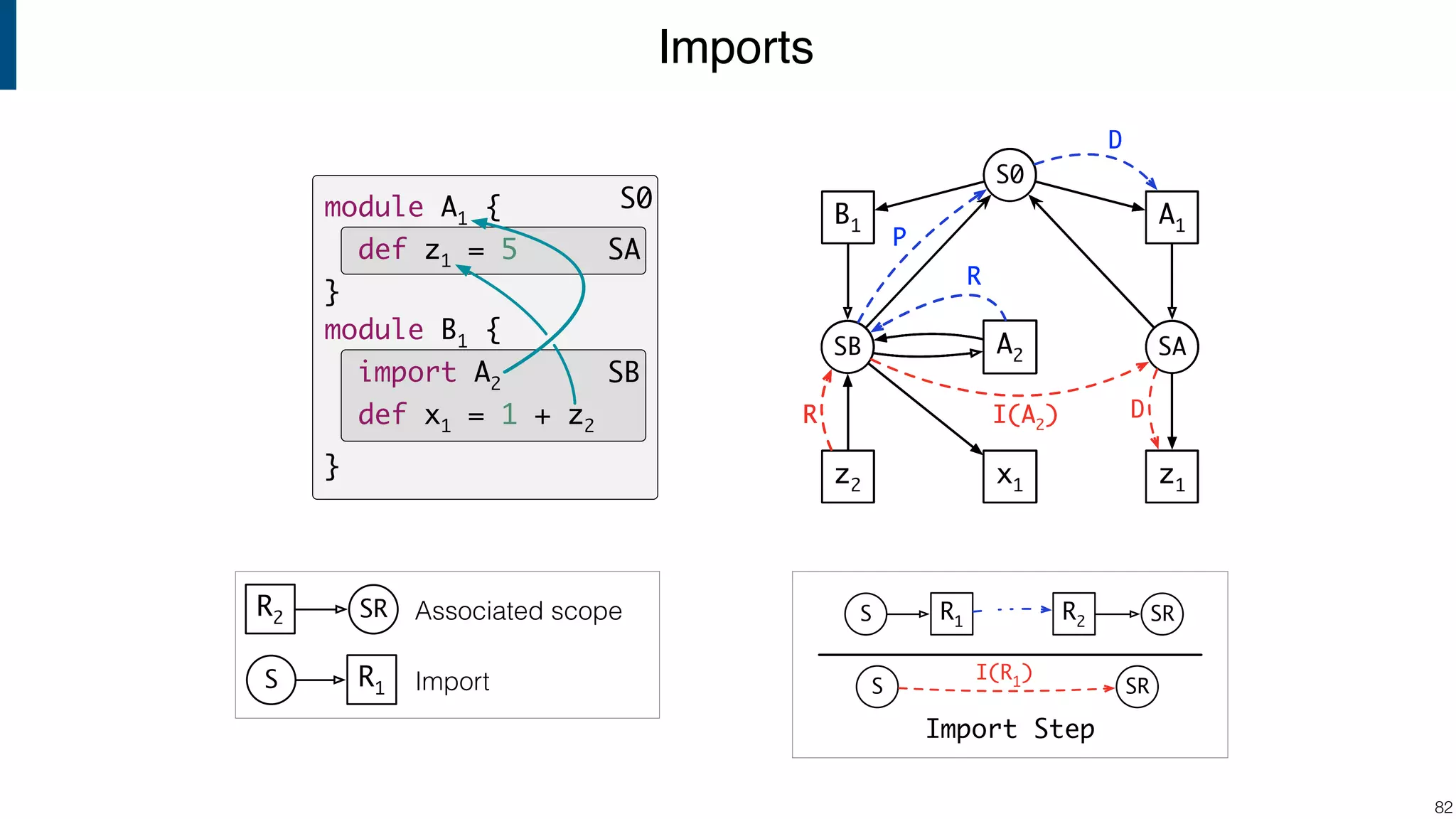
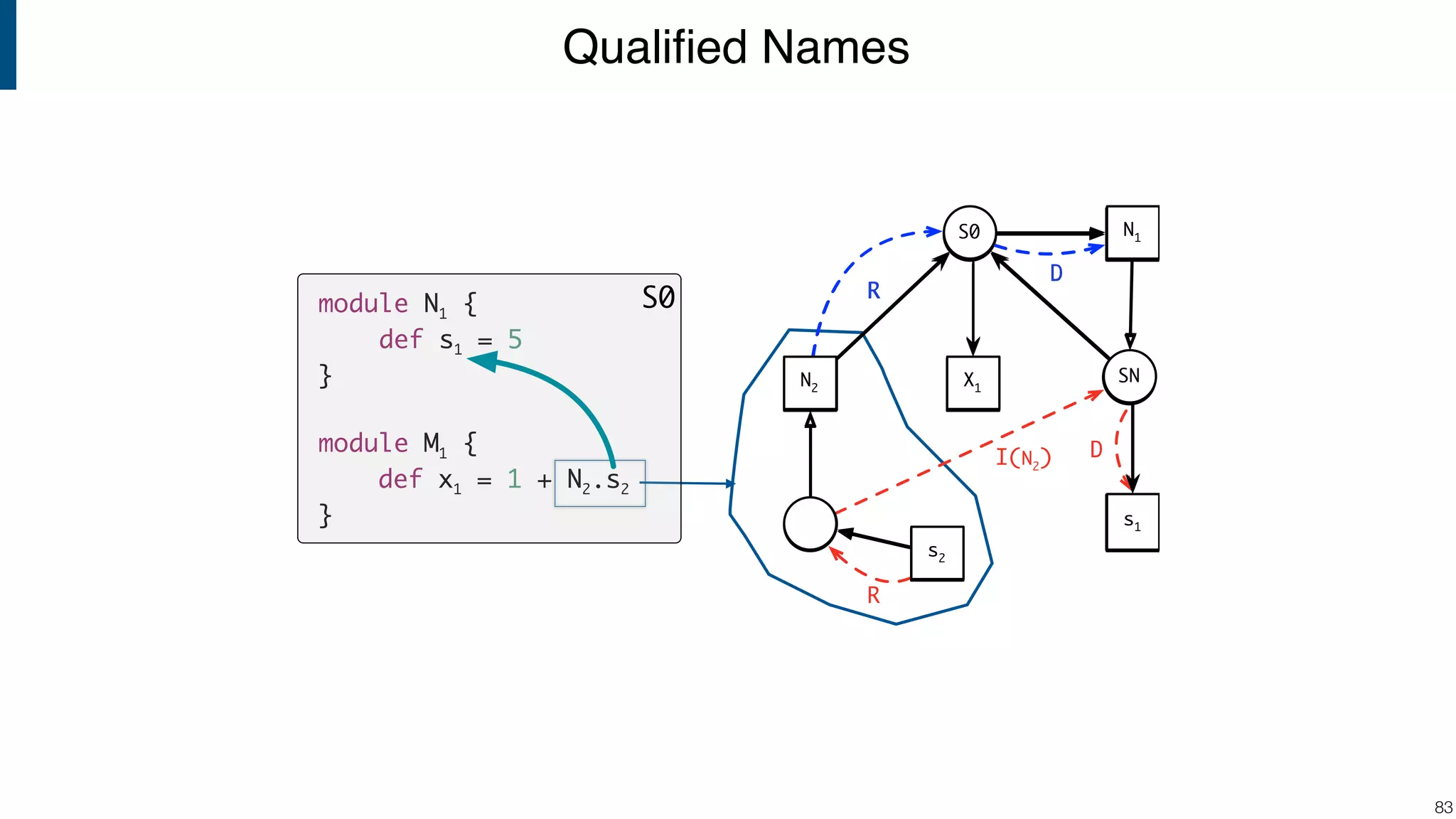
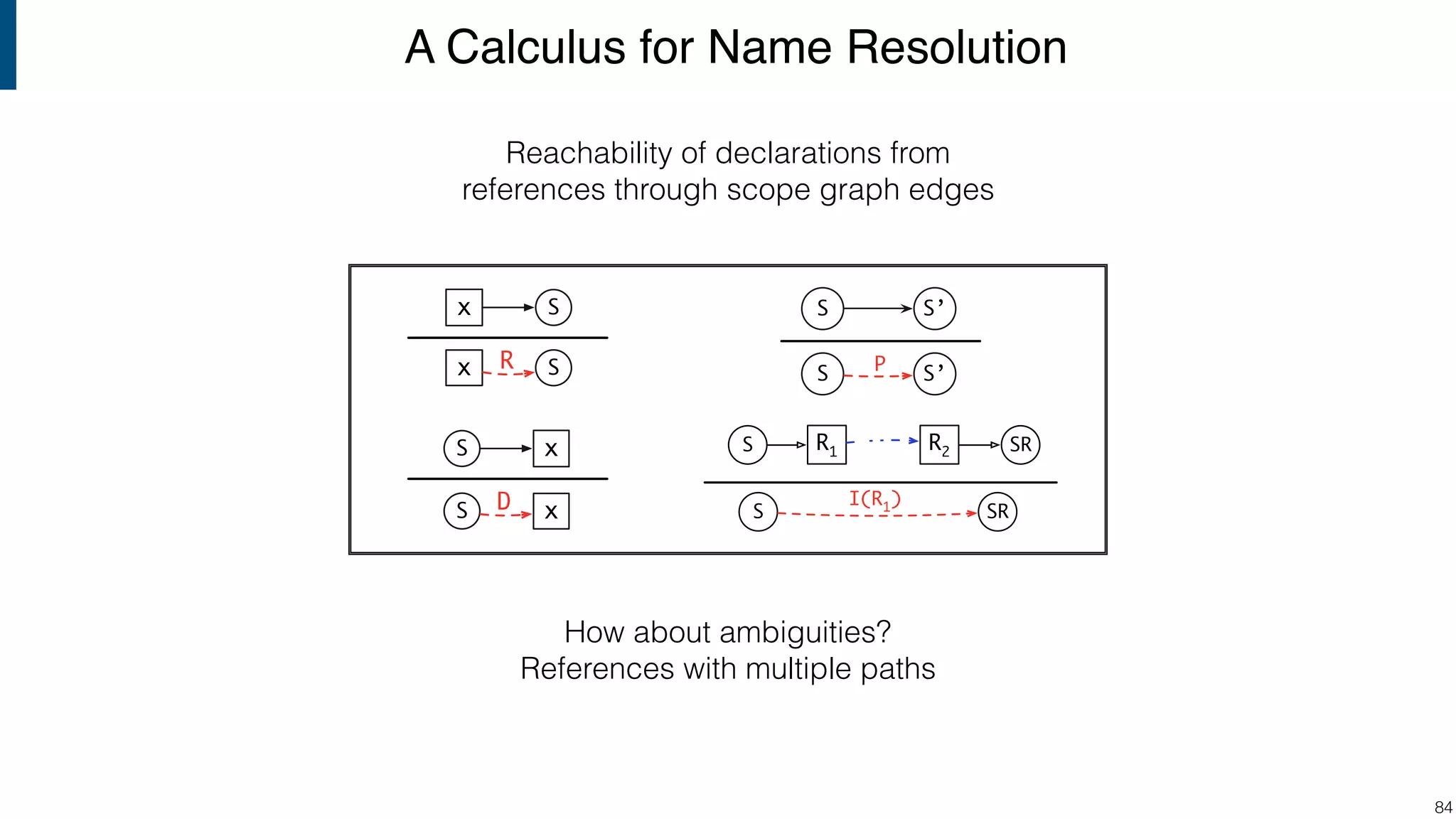
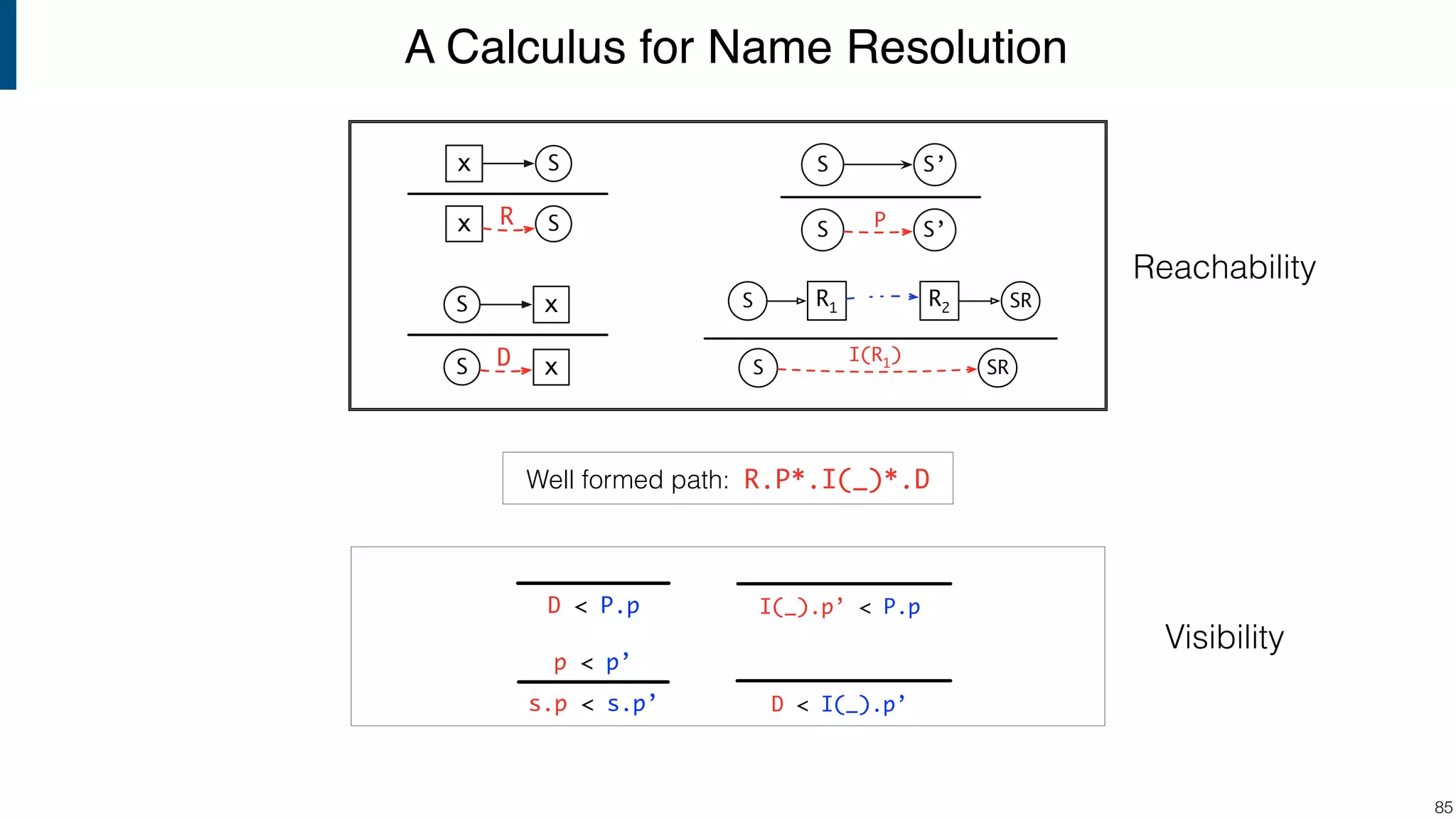
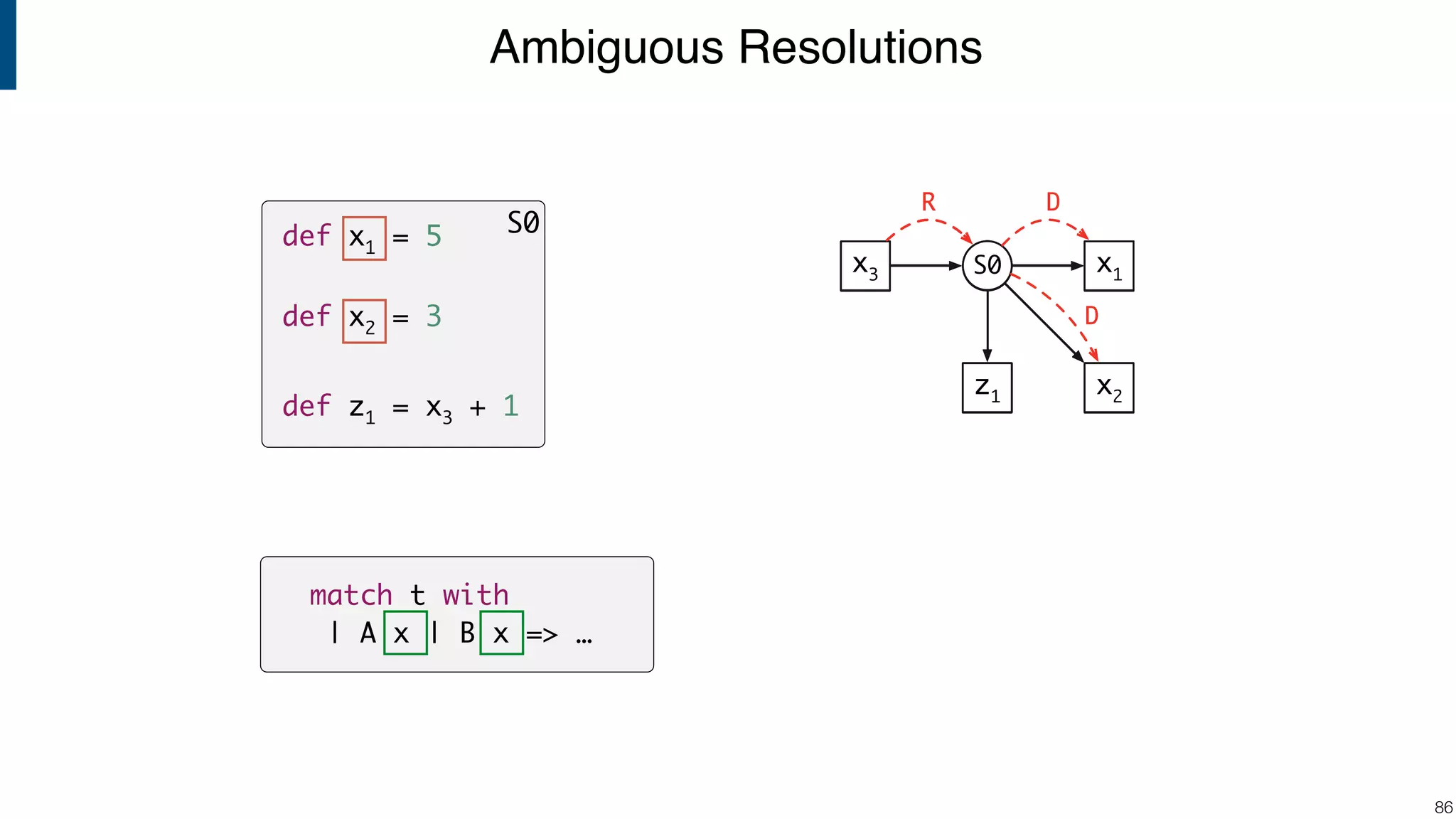
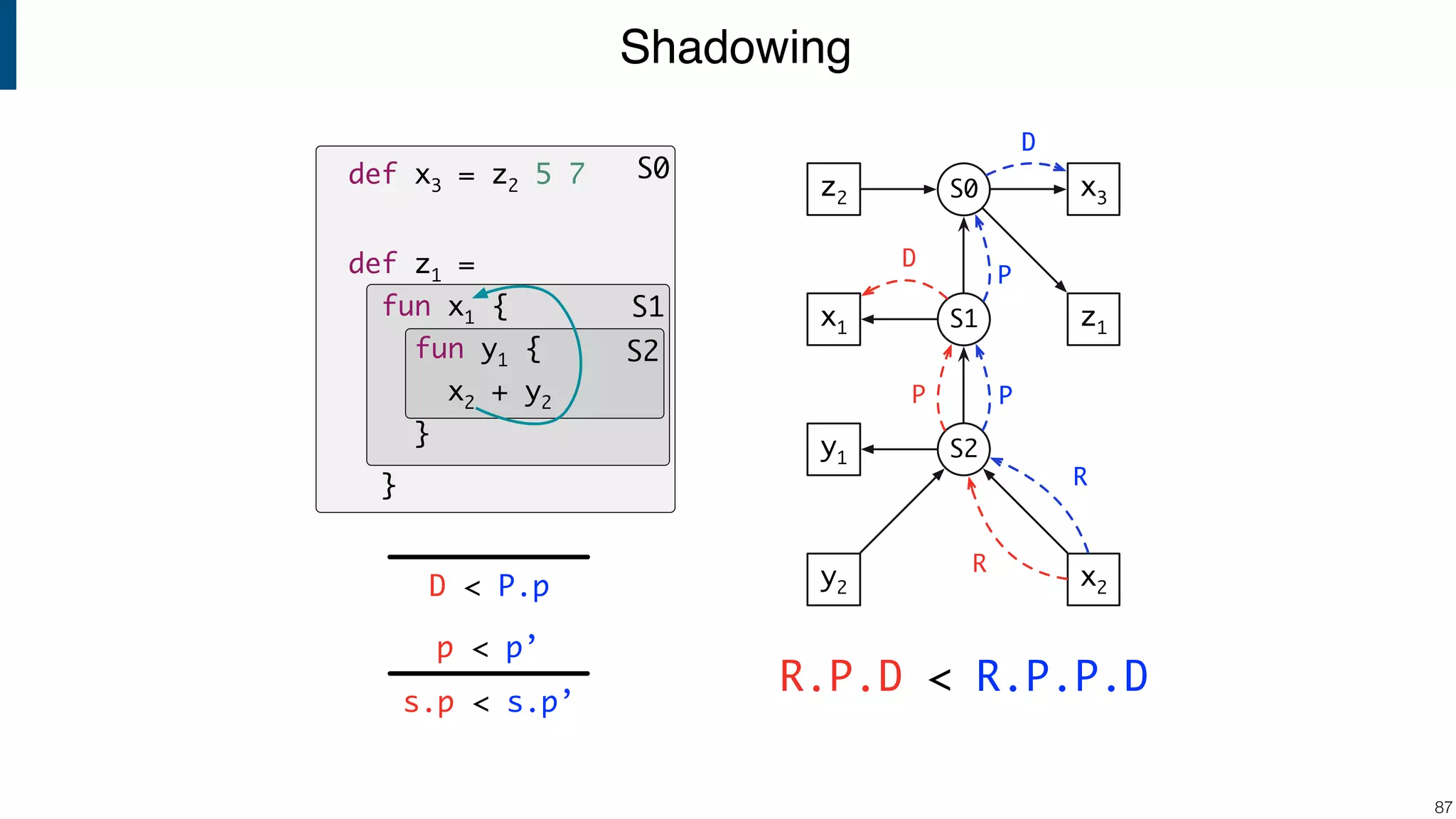
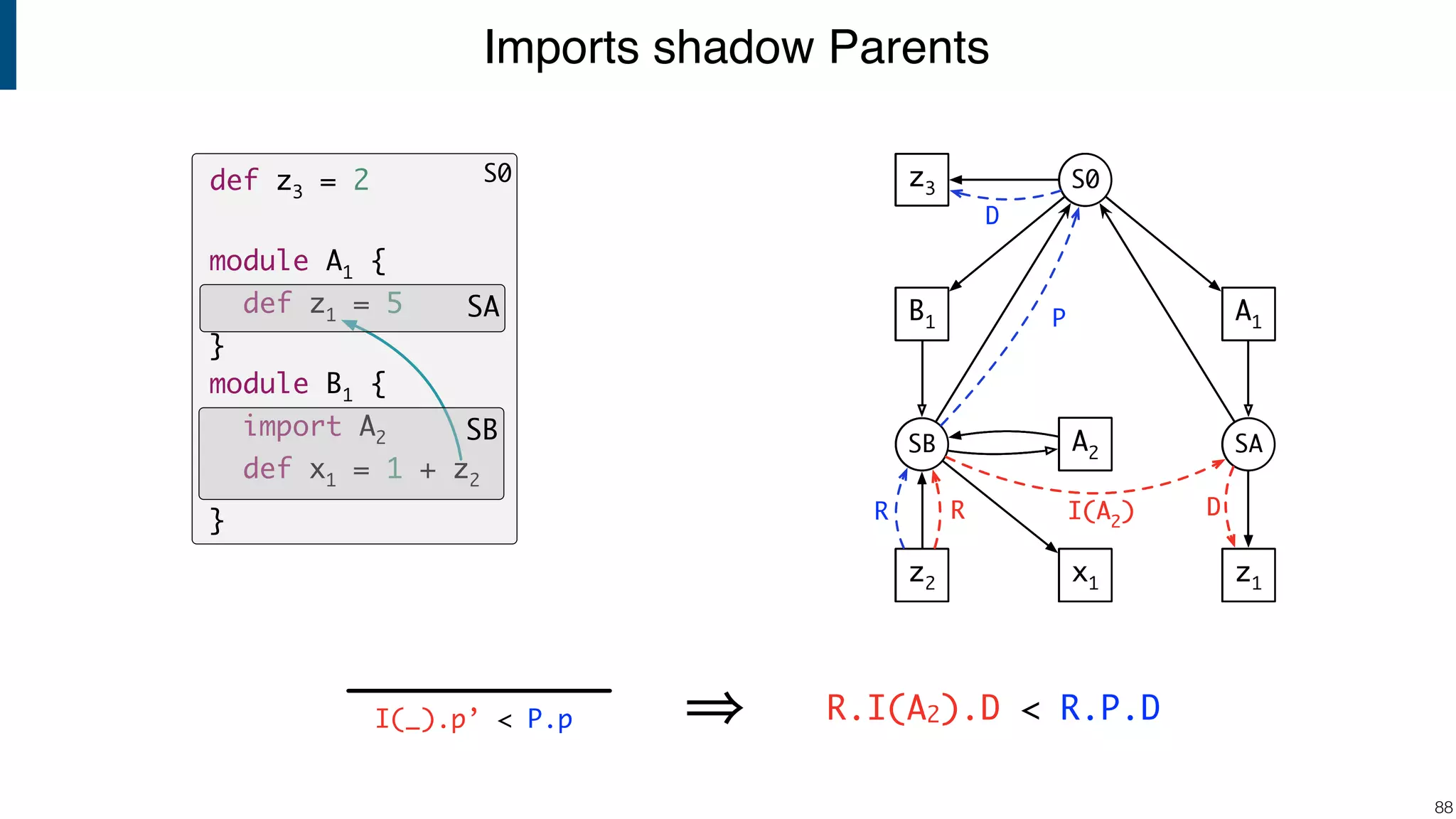
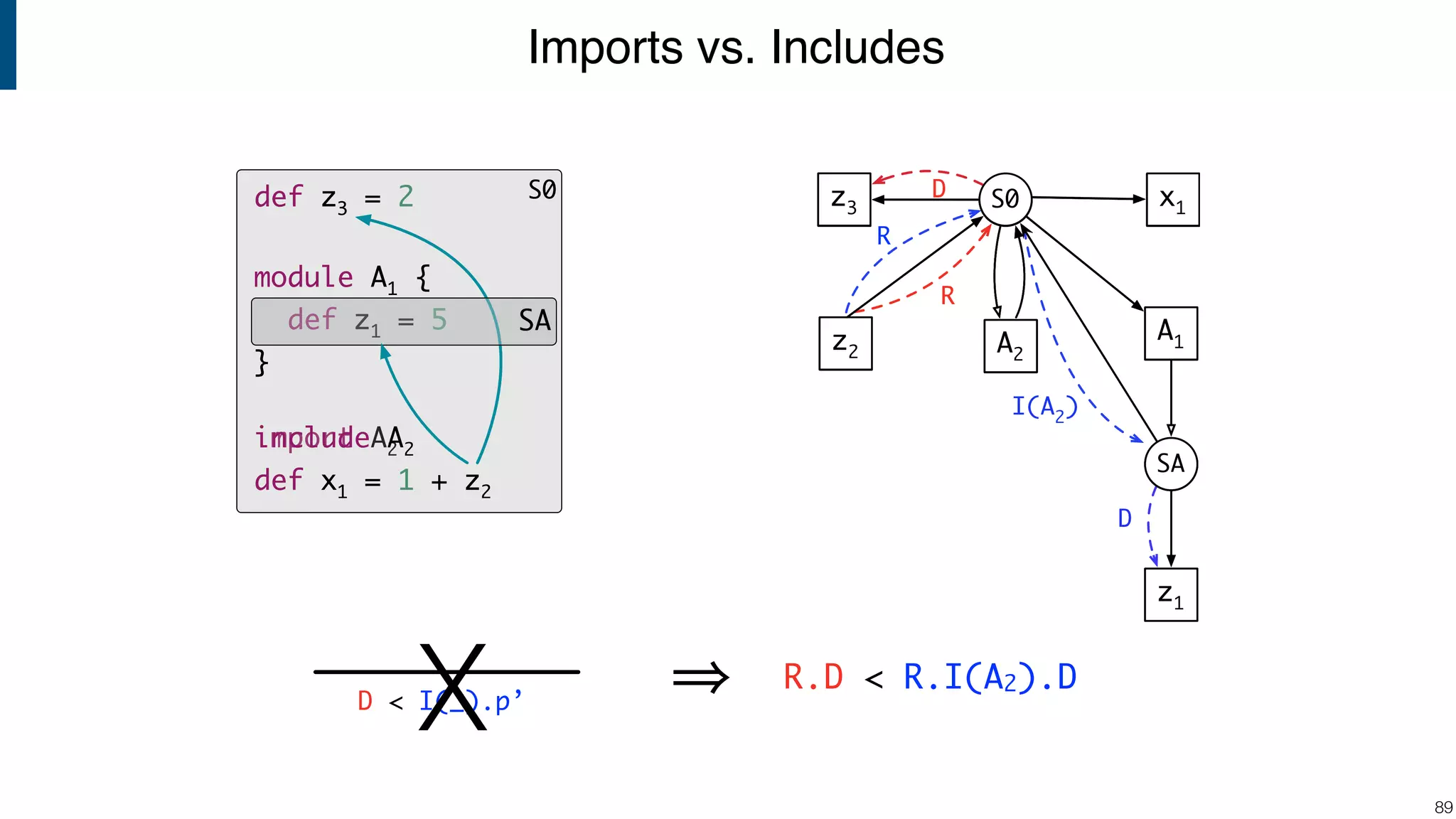
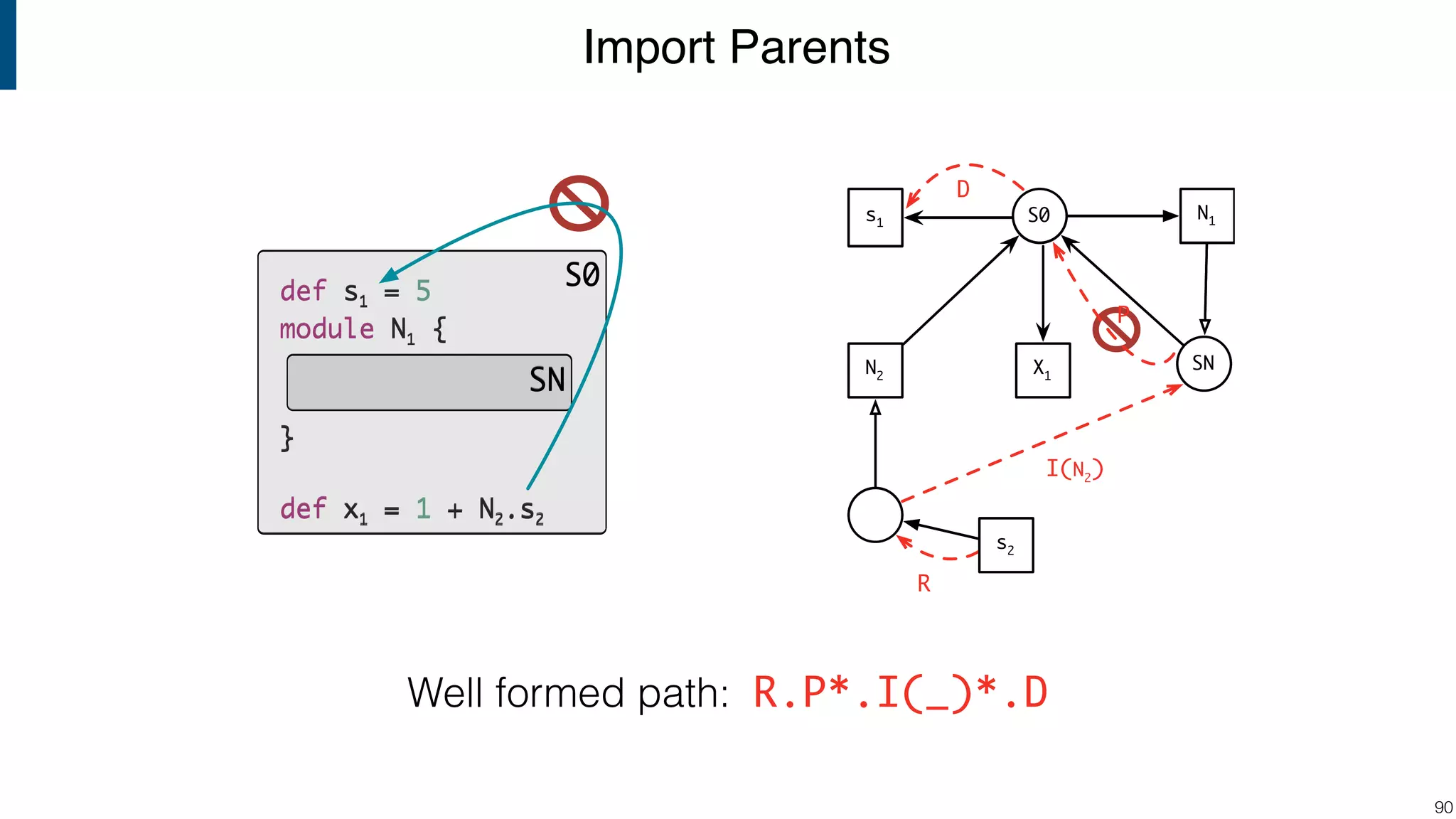
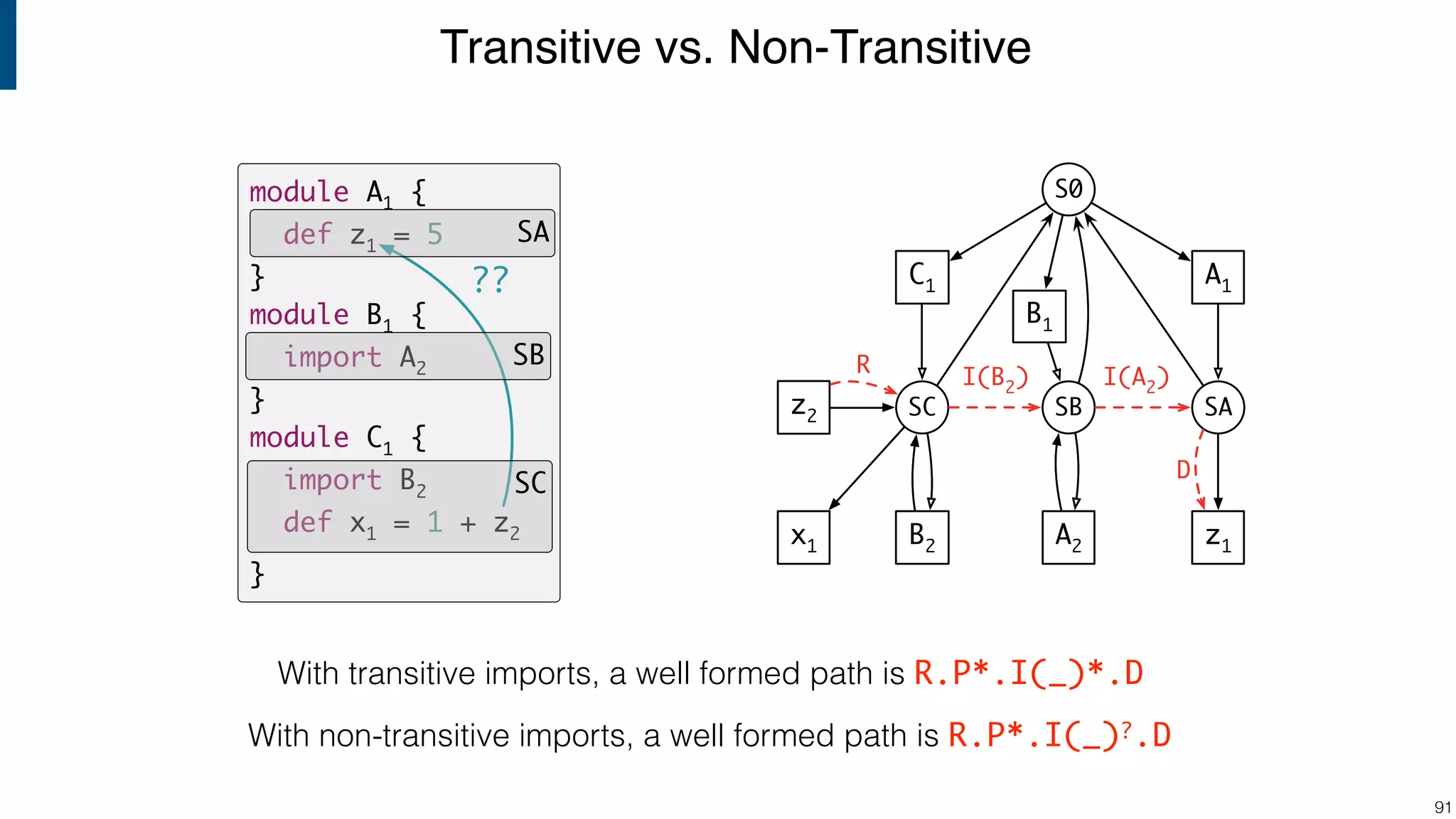
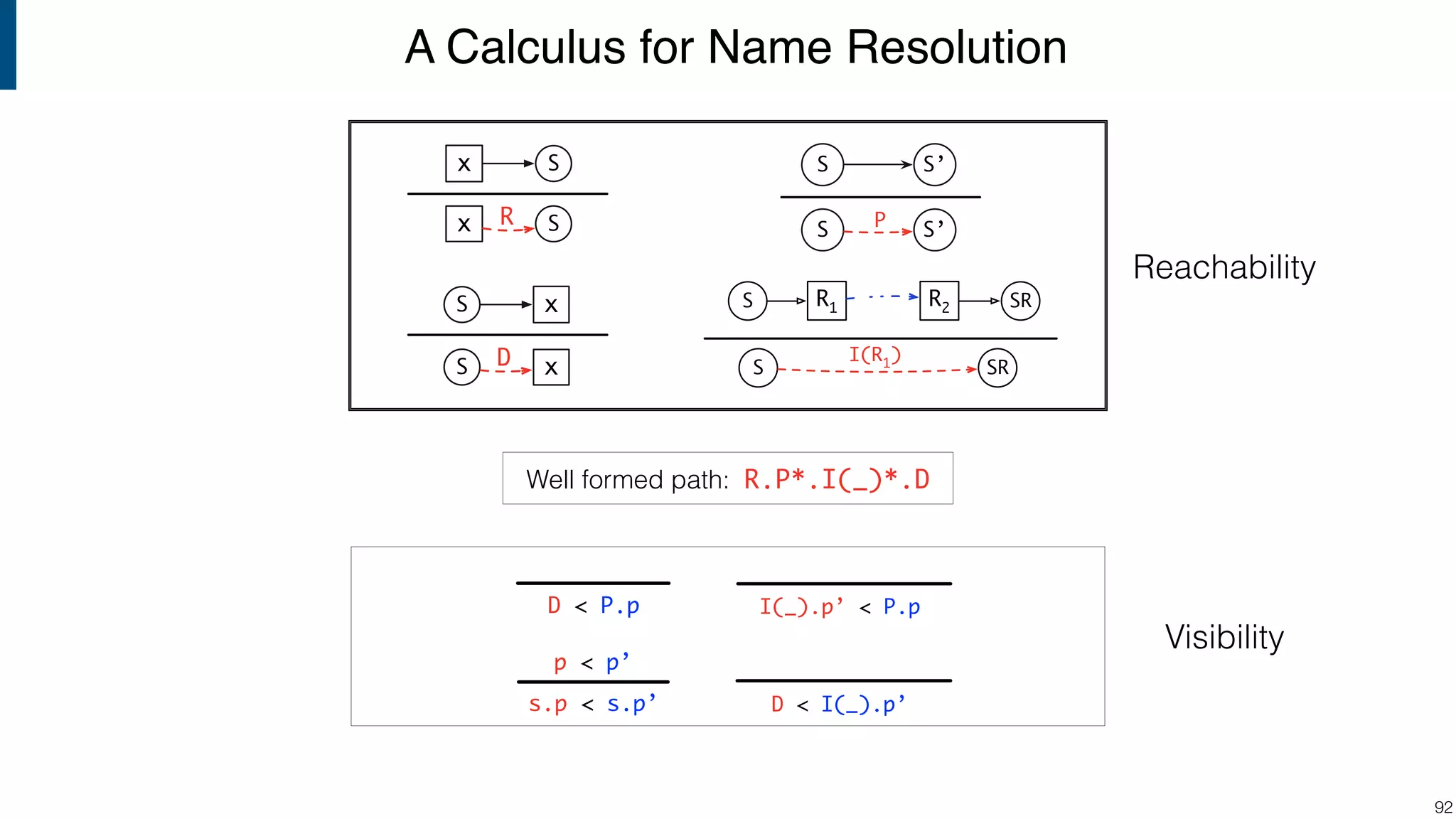


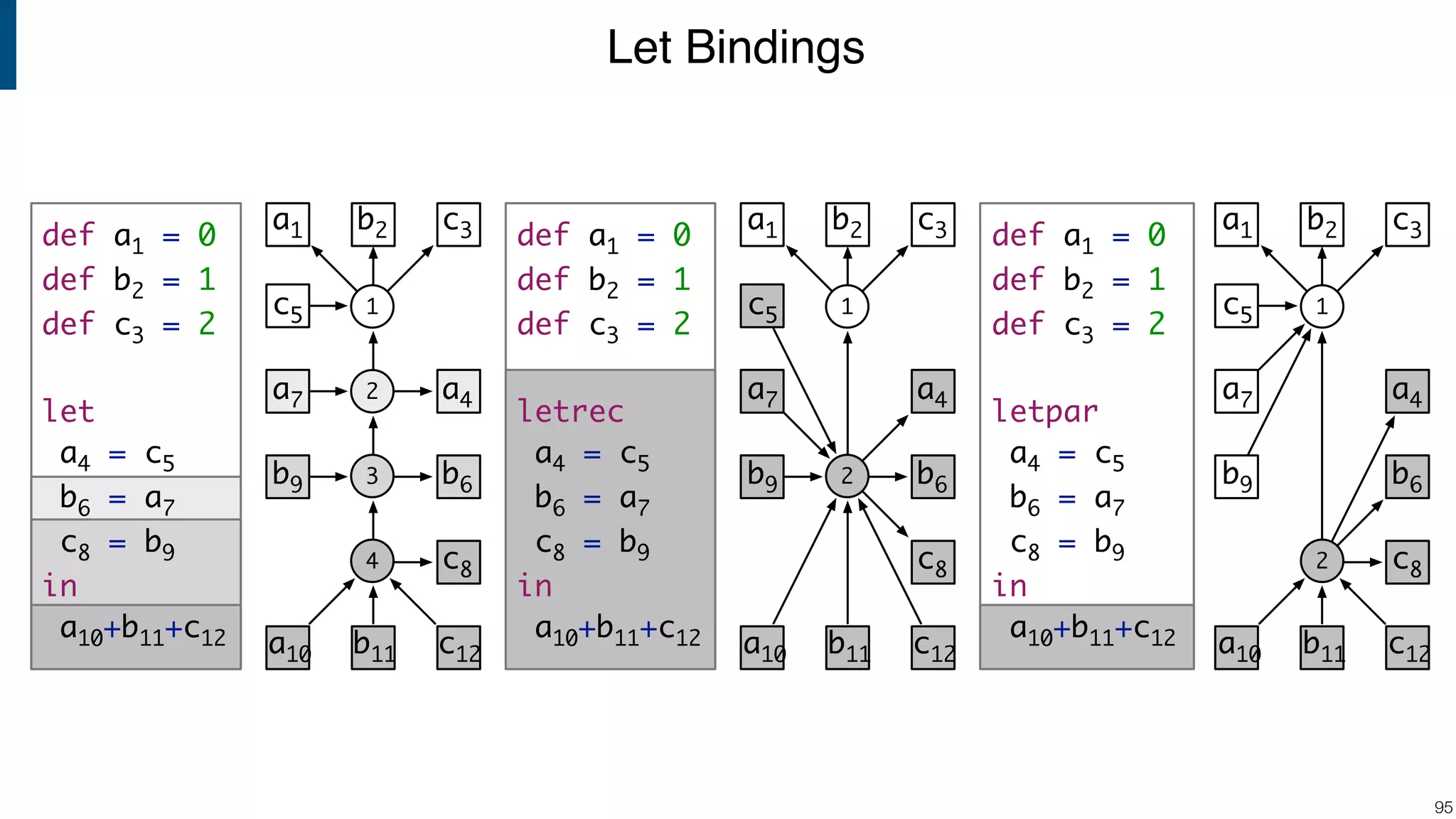
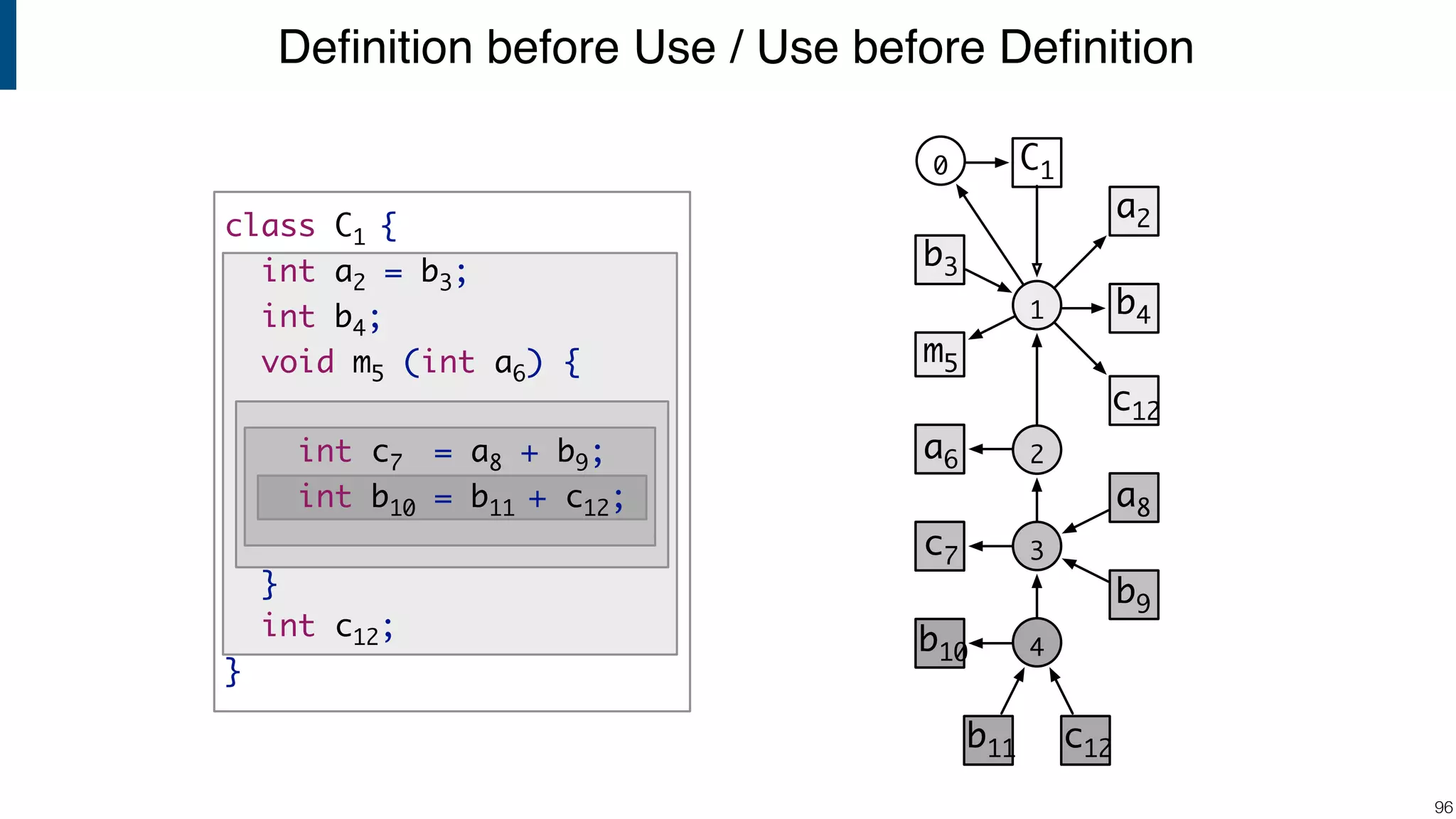
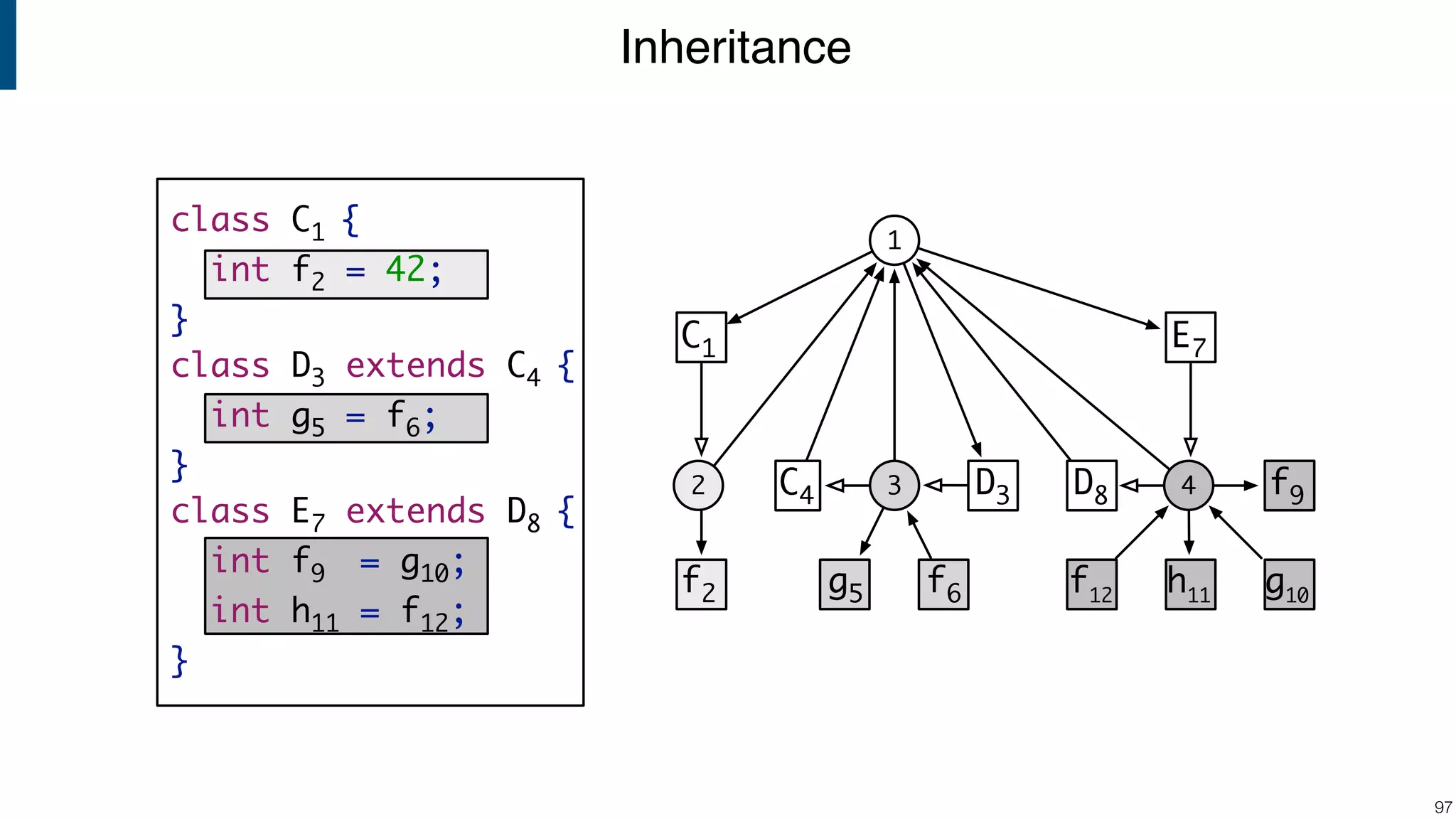
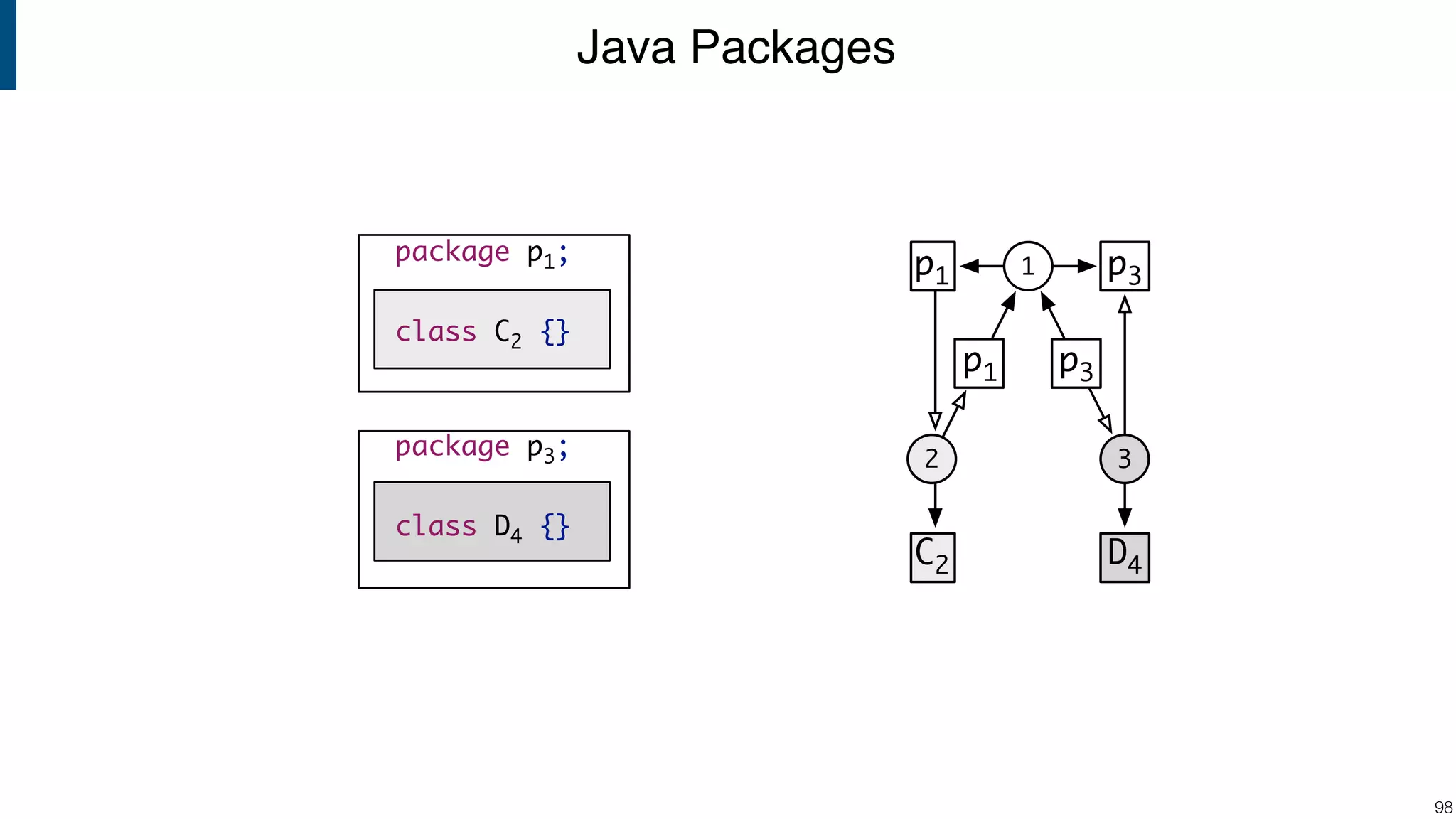
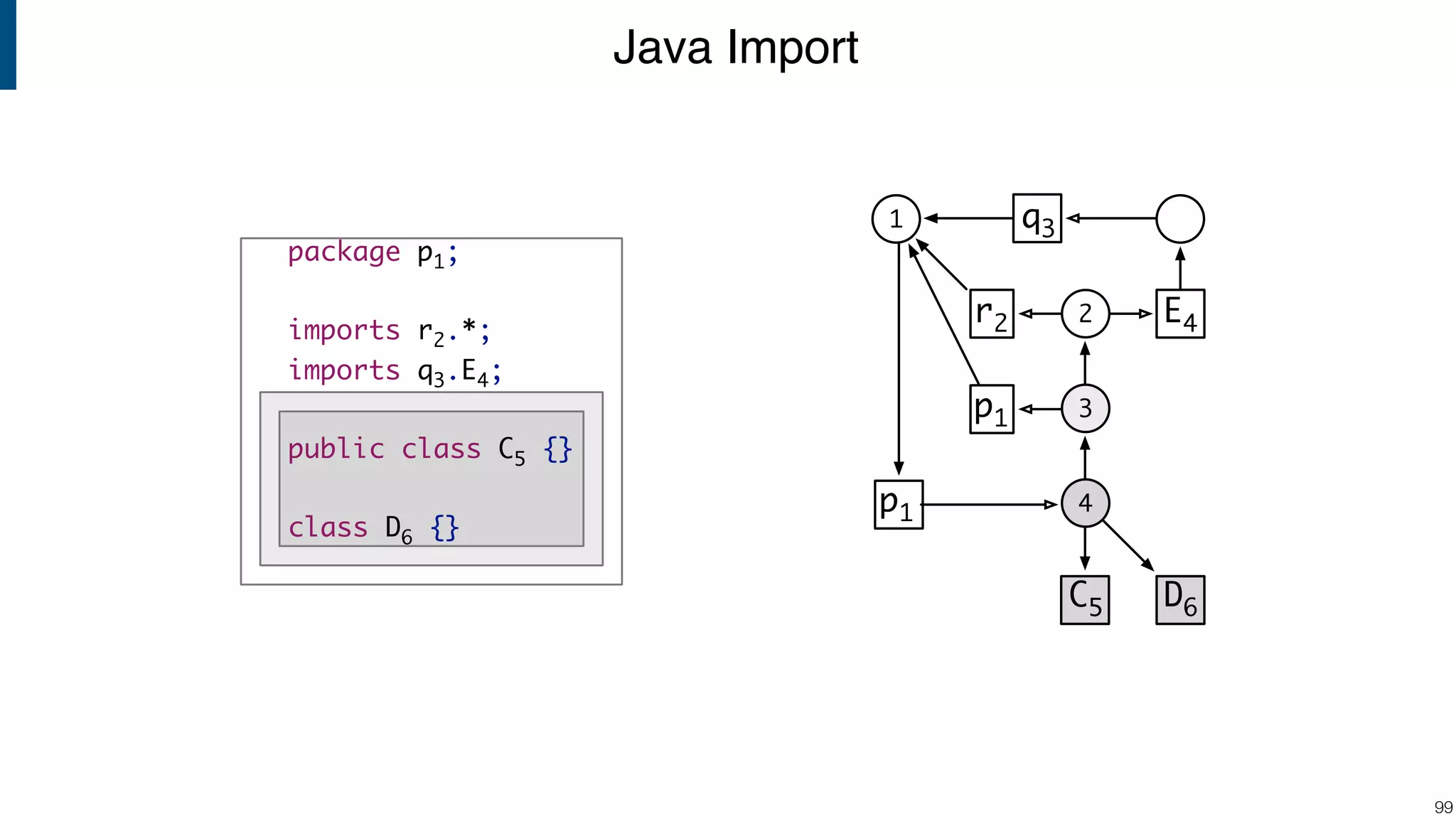
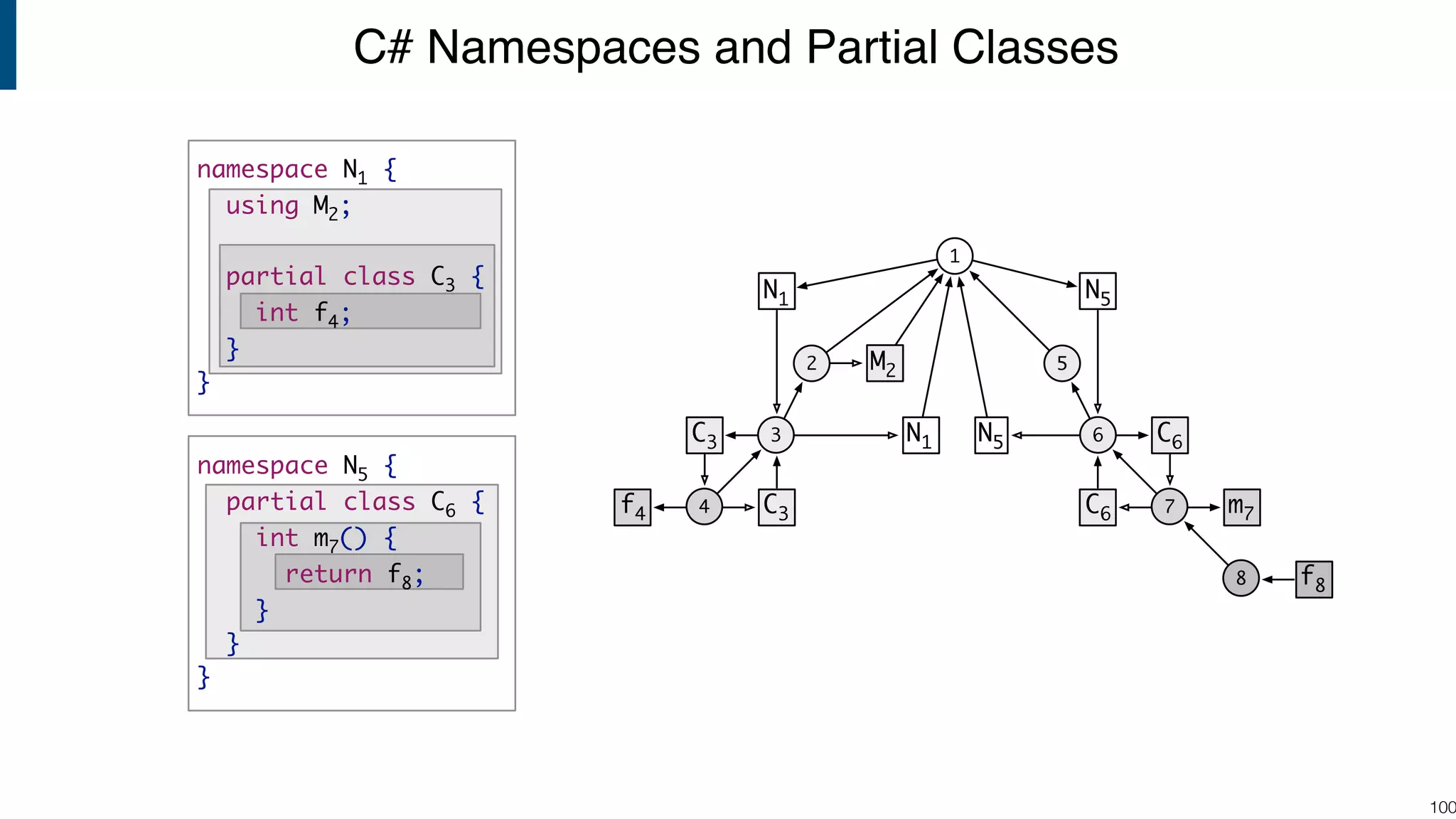




![Scope graph semantics for binding languages [OOPSLA18] - starting with NaBL - or rather: a redesign of NaBL based on scope graphs Dynamic analogs to static scope graphs [ECOOP16] - how does scope graph relate to memory at run-time? Supporting mechanized language meta-theory [POPL18] - relating static and dynamic bindings Resolution-sensitive program transformations - renaming, refactoring, substitution, … !105 Ongoing/Future Work](https://image.slidesharecdn.com/cs4200-2018-6-intro-to-static-analysis-181002210659/75/Compiler-Construction-Lecture-6-Introduction-to-Static-Analysis-105-2048.jpg)



![Representation - ? Declarative Rules - ? Language-Independent Tooling - Name resolution - Code completion - Refactoring - … !109 Separation of Concerns in Name Binding Scope & Type Constraint Rules [PEPM16] Scope Graphs](https://image.slidesharecdn.com/cs4200-2018-6-intro-to-static-analysis-181002210659/75/Compiler-Construction-Lecture-6-Introduction-to-Static-Analysis-109-2048.jpg)