coding.pdf

Information Network Security Administration Intelligence Technology Excellence Division Signal Analyst Team Module-II Phase-I Presentation on: By: Mebit Birara January , 2023 Arithmetic coding and Low density parity check (LDPC) codes

Outline ➢ Arithmetic coding ❖Algorithms ❖Examples ❖Characterization ❖Comparison ➢ Low density parity check (LDPC) codes ❖ Introduction ❖ Types of LDPC codes ❖ LDPC Code Properties ❖ Construction of Parity Check Matrix H ❖ Graphical Representation ❖ LDPC Encoding

Arithmetic coding ❑ Arithmetic coding is a more modern coding method that usually out- performs Huffman coding. ❑ Huffman coding assigns each symbol a codeword which has an integral bit length. Arithmetic coding can treat the whole message as one unit. ❑ A message is represented by a half-open interval [a, b) where a and b are real numbers between 0 and 1. Initially, the interval is [0, 1). When the message becomes longer, the length of the interval shortens and the number of bits needed to represent the interval increases.

Arithmetic coding ❑ In arithmetic coding a message is encoded as a number from the interval [0, 1). ❑ The number is found by expanding it according to the probability of the currently processed letter of the message being encoded. ❑ This is done by using a set of interval ranges IR determined by the probabilities of the information source as follows: IR={[0,𝑝1),[𝑝1,𝑝1+𝑝2),[ca𝑝1 + 𝑝2,𝑝1 + 𝑝2 + 𝑝3),…[𝑝1+…+𝑝𝑛−1, 𝑝1+…+𝑝𝑛)} Putting,𝑞𝑗 = σ𝑖=1 𝑗 𝑝𝑖, we n write IR ={[0,𝑞1),[𝑞1, 𝑞2),[𝑞𝑛−1,1) ❑ In arithmetic coding these subintervals also determine the proportional division of any other interval [L, R) contained in [0, 1) into subintervals 𝐼𝑅[𝐿,𝑅] as follows:

algorithms 𝐼𝑅[𝐿,𝑅] = {[𝐿, 𝐿 + (𝑅 − 𝐿) 𝑞1),[L+(R-L) 𝑞1,L+(R-L) 𝑞2), [𝐿 + 𝑅 − 𝐿 𝑞2, 𝐿 + (𝑅 − 𝐿) 𝑞3),[L+(R-L) 𝑞𝑁−1,L+(R-L))} ❑ Using these definitions the arithmetic encoding is determined by the Following algorithm: ArithmeticEncoding ( Message ) 1. CurrentInterval = [0, 1); While the end of message is not reached 2. Read letter 𝒙𝒊 from the message; 3. Divid CurrentInterval into subintervals 𝑰𝑹𝑪𝒖𝒓𝒓𝒆𝒏𝒕𝑰𝒏𝒕𝒆𝒓𝒗𝒂𝒍; Output any number from the CurrentInterval (usually its left boundary);

Examples Examples: consider the transmission of a message “mekonen” comprising a string of characters with probability. Solution: take the following procedures. Procedures: Step1: divide the numerical range 0 to 1 into number of different symbol present in the message. Step2: expand the first latter to be coded along with the range. further subdivide this range into number of symbols. Step3: repeat the procedures until termination character is encoded.

Examples The source message is “mekonen”. d=upper bound-lower bound Range of symbol=lower limit : d(probability of symbol) symbol probability Initial range e 0.2857 [0,0.2857) k 0.1429 [0.2857,0.4286) m 0.1429 [0.4286,0.5714) n 0.2857 [0.5714,0.8571) o 0.1429 [0.8571,1)

Examples 1 0.5714 0.4694 0.4461 0.4461 0.4459 0.4457 0.4457 o o o o o o o 0.8571 0.5510 0.4636 0.4453 0.4459 0.4459 0.4457 n n n n n n n 0.5714 0.5102 0.4519 0.4436 0.4456 0.4458 0.4457 m m m m m m m 0.4286 0.4898 0.4461 0.4428 0.4456 0.4457 0.4456 k k k k k k k 0.2857 0.4694 0.4403 0.4420 0.4455 0.4457 0.4456 e e e e e e e 0 0.4286 0.4286 0.4403 0.4453 0.4456 0.4456 0.4457

Examples Lets calculate each interval based on algorithms by take iteration i: For i=1: d=high-low=1-0=1 L(e)=0, U(e)=0+1(0.2857)=0.2857 L(K)=0.2857=U(e), U(K)=0.2857+1(0.1429)=0.4286 L(m)=0.4286=U(k) U(m)=0.4286+1(0.1429)=0.5714 L(n)=0.5714=U(k) U(n)=0.5714+1(0.2857) =0.8571 L(o)=0.8571=U(n) U(o)=0.8571+1(0.1429) =1 For i=2 d=0.5714-0.4286=0.1428 L(e)=0.4286 U(e)=0.4286+0.1428(0.2857) =0.4694 L(K)=0.4694=U(e) U(K)=0.4694+0.1428(0.1429)=0.4898

Examples L(m)=0.4898=U(k) U(m)=0.4898+0.1428(0.1429)=0.5102 L(n)=0.5102=U(m) U(n)=0.5102+0.1428(0.1429)=0.5510 L(o)=0.5510=U(n) U(o)=0.5510+0.1428(0.1429)=0.5714 For i=3 d=0.4694-0.4286=0.0408 L(e)=0.4286 U(e)=0.4286+0.0408(0.2857)=0.4403 L(k)=0.4403=U(e) U(k)=0.4403+0.0408(0.1429)=0.4461 L(m)=0.4461=U(k) U(m)=0.4461+0.0408(0.1429)=0.4519 L(n)=0.4519=U(m) U(n)=0.4519+0.0408(0.2857)=0.4636 L(o)=0.4636=U(n) U(o)=0.4636+0.0406(0.1429)=0.4694

Examples For i=4 d=0.4461-0.4403=0.0058 L(e)=0.4403 U(e)=0.4403+0.0058(0.2857)=0.4420 L(k)=0.4420=U(e) U(k)=0.4420+0.0058(0.1429)=0.4428 L(m)=0.4428=U(k) U(m)=0.4428+0.0058(0.1429)=0.4436 L(n)=0.4436=U(m) U(n)=0.4436+0.0058(0.2857)=0.4453 L(o)=0.4453=U(n) U(o)=0.4453+0.0058(0.1429)=0.4461 For i=5 d=0.4461-0.4453=0.0008 L(e)=0.4453 U(e)=0.4453+0.0008(0.2857)=0.4455 L(k)=0.4455=U(e) U(k)=0.4455+0.0008(0.1429)=0.4456

Examples L(m)=0.4456=U(k) U(m)=0.4456+0.0008(0.1429)=0.4456 L(n)=0.4456=U(m) U(n)=0.4456+0.0008(0.2857)=0.4459 L(o)=0.4459=U(n) U(o)=0.4459+0.0008(0.1429)=0.4461 For i=6 d=0.4459-0.4456=0.0003 L(e)=0.4456 U(e)=0.4456+0.0003(0.2857)=0.4457 L(k)=0.4457=U(e) U(k)=0.4457+0.0003(0.1429)=0.4457 L(m)=0.4457=U(k) U(m)=0.4457+0.0003(0.1429)=0.4458 L(n)=0.4458=U(m) U(n)=0.4458+0.0003(0.2857)=0.4459 L(o)=0.4459=U(n) U(o)=0.4459+0.0003(0.1429)=0.4459

Examples For i=7 d=0.4457-0.4456=0.0001 L(e)=0.4456 U(e)=0.4456+0.0001(0.2857)=0.4456 L(k)=0.4456=U(e) U(k)=0.4456+0.0001(0.1429)=0.4456 L(m)=0.4456=U(k) U(m)=0.4456+0.0001(0.1429)=0.4457 L(n)=0.4457=U(m) U(n)=0.4457+0.0001(0.2857)=0.4457 L(o)=0.4457=U(n) U(o)=0.4457+0.0001(0.1429)=0.4457 Therefore the interval of the termination character “n” is [0.4457,0.4457).The output is any number between the interval of last character. Mostly take the average or left interval(lower limit).

Characterization So, the codeword is bounded as follows: 0.4457<=codeword<0.4457 Codeword=0.4457. Characterization: ➢ One codeword for the whole message ➢ Message is represented by a (small) interval in [0, 1) ➢ Each successive symbol reduces the interval size ➢ Interval size = product of symbol probabilities ➢ Final code = any value from the interval

Comparison Comparison of arithmetic and Huffman encoding: ❑ Arithmetic coding is more complicated that the Huffman coding ,but arithmetic coding allows us to code sequence of symbols. ❑ The efficiency of arithmetic code is always better or at least identical to Huffman code, because generating only one tag for the complete message. ❑ The major disadvantage of Huffman code is that even if there is a small change in the code, the entire message is lost. ❑ A fixed number of bits are used in Arithmetic coding which gives better compression ratio but increases the compression time. ❑ It is concluded that Huffman coding surpasses other algorithms for real time applications.

Comparison Comparession tables: Compression method Arithmetic Huffman Compression ratio Very good good Compression speed Slow Fast Decompression speed Slow Fast

Low density parity check(LDPC) codes ❑ Low density parity check (LDPC) codes are forward error-correction codes, invented by Robert Gallager in his MIT Ph.D. dissertation, 1960. ❑ The LDPC codes are ignored for long time due to their high computational complexity and domination of highly structured algebraic block and convolutional codes for forward error correction. ❑ A number of researchers produced new irregular LDPC codes which are known as new generalizations of Gallager’s LDPC codes that outperform the best turbo codes with certain practical advantages. ❑ LDPC codes have already been adopted in satellite based digital video broadcasting and long-haul optical communication standards.

Low density parity check(LDPC) codes LDPC Code Properties ❑ Low Density Parity Check (LDPC) code is a linear error-correcting code that has a parity check matrix H, which is sparse i.e. with less nonzero elements in each row and column. ❑ LDPC codes can be categorized into: 1.regular and 2.irregular LDPC codes. When the parity-check matrix 𝐻 𝑛−𝑘 ×𝑛 has the same number 𝑤𝑐 of ones in each column and the same number 𝑤𝑟 of once in each row, the code is a regular (𝑤𝑐, 𝑤𝑟).

Low density parity check(LDPC) codes ❑ The original Gallager codes are regular binary LDPC codes. The size of H is usually very large, but the density of nonzero element is very low. ❑ LDPC code of length n, or denoted as an (n, 𝑤𝑐, 𝑤𝑟) LDPC code. Thus, each information bit is involved with 𝑤𝑐 parity checks, and each parity-check bit is involved with , 𝑤𝑟 information bits. ❑ Irregular LDPC codes have different number of 1’s in each rows and in each columns. ❑ Fundamentals of LDPC Codes: 1.Parity-check matrices(H) 2.Tanner graph (TGs)

Low density parity check(LDPC) codes Construction of Parity Check Matrix H Gallager Codes ❑ Gallager first proposed regular LDPC codes with three parameters (n, 𝑤𝑐, 𝑤𝑟) to denote the code length, the number of 1s in each column, and the number of 1s in each row, respectively. ❑ A parity-check matrix H for Gallager codes is constructed by random column permutations, and has the following structure: 1. The parity-check matrix H can be split into 𝑤𝑐 submatrices 𝐻1, 𝐻2, . . . , 𝐻𝑤𝑐 .

Low density parity check(LDPC) codes 2.The matrix 𝐻1 has n columns and n/𝑤𝑟 rows . ❑ The 𝐻1 contains a single 1 in each column and contains 1s in its ith row from column (i-1) 𝑤𝑟+1 to column i(𝑤𝑟). ❑ For 𝐻1 the row elements equal to 1 are arranged in sloping fashion. 3. Permuting randomly the columns of 𝐻1 with equal probability, the matrices 𝐻1 to 𝐻𝑤𝑐 are obtained. ❑ Finally the parity check matrices H have n/𝑤𝑟(𝑤𝑐) rows and n columns.

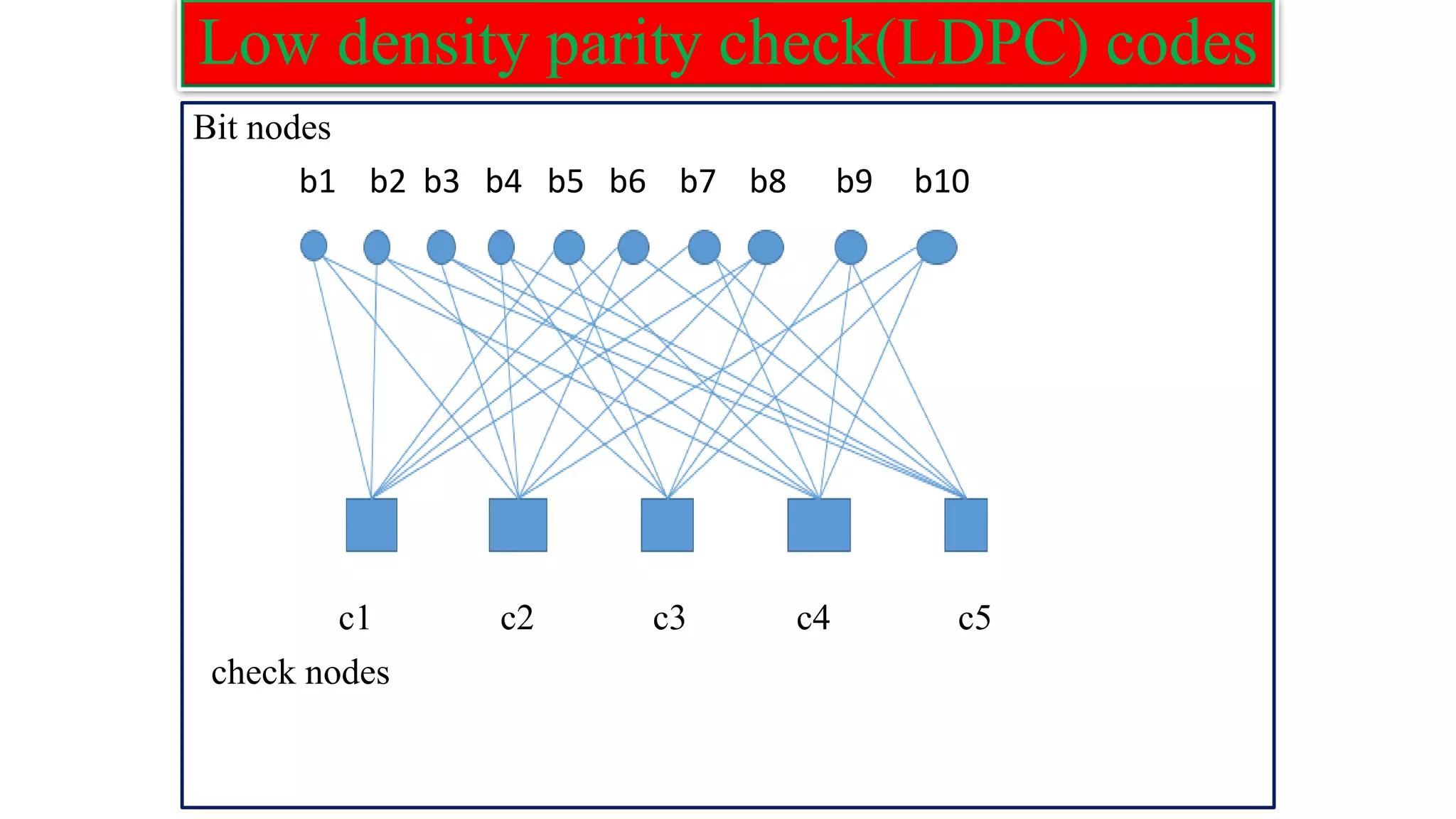
Low density parity check(LDPC) codes Examples :The parity check matrix for (n=20, 𝑤𝑐=3, 𝑤𝑟=4) code constructed by Gallager is given as: H= [𝐻1 𝐻2 𝐻3] 𝐻1 Rows of : 𝐻1=n/𝑤𝑟=20/4=5 Columns of: 𝐻1=n=20 𝐻2 Rows of H: m= n/𝑤𝑟(𝑤𝑐) =5*3=15 Columns of H: n=20 𝐻3

Low density parity check(LDPC) codes Graphical Representation ❑ Tanner studied LDPC codes and illustrated how they can be represented by the so-called Tanner graph, or TG for brevity, which is similar to the trellis graph of a convolutional code in the sense of facilitating description of the code and relevant algorithms. ❑ A TG is a bipartite graph whose nodes are separated into two categories: 1. variables nodes (or symbol nodes) 2. check nodes (or constraint nodes) Bit nodes or variable nodes (VN) equal to the number of columns of H, and check nodes (CN) equal to the number of rows of H.

Low density parity check(LDPC) codes ❑ If 𝐻𝑗𝑖=1,(if variable i participates in the jth parity-check constraint), then check node j is connected to variable node i . Example: Construct Tanner graph for the following parity check matrix. H= Number of bit nodes: VN= 10 ,which is represent by circle. Number of check nodes: CN=5,which is represent by rectangle.

Low density parity check(LDPC) codes Bit nodes b1 b2 b3 b4 b5 b6 b7 b8 b9 b10 c1 c2 c3 c4 c5 check nodes

Low density parity check(LDPC) codes LDPC Encoding 1.Preprocessing Method ❑ Derive a generator matrix G from the parity check matrix H for LDPC codes by means of Gaussian elimination in modulo-2 arithmetic. ❑ As such this method can be viewed as the preprocessing method. 1-by-n code vector c is first partitioned as: C=[b:m] where m is k by 1message vector, and b is the n−k by 1 parity vector correspondingly. ❑ The parity check matrix H is partitioned as: 𝐻𝑇 =[𝐻1;𝐻2]; where H1 is a square matrix of dimensions (n − k)×(n − k), and H2 is a rectangular matrix of dimensions k × (n − k).

Low density parity check(LDPC) codes ❑ Imposing the constraint C𝐻𝑇=0. [b:m][𝐻1;𝐻2]=0 or equivalently b𝐻1+m𝐻2=0. ❑ The vectors m and b are related by: b=mp ,p=𝐻2𝐻1 −1 ❑ where 𝐻1 −1 is the inverse matrix of 𝐻1, which is naturally defined in modulo-2 arithmetic. ❑ Finally, the generator matrix of LDPC codes is defined by: G=[p:𝐼𝑘] = [𝐻2𝐻1 −1 :𝐼𝑘]

Low density parity check(LDPC) codes ❑ The codeword can be generated as: C=mG Example: Construct LDPC code word for the following parity check matrix with the message vector m = [1 0 0 0 1]. H= Solution: The parity check matrix H is of the order 5 X 10 . ❑ We know that 𝑯𝑻 =[𝐻1;𝐻2]

Low density parity check(LDPC) codes 𝑯𝑻 = 𝐻1= 𝐻2=

Low density parity check(LDPC) codes ❑ Letting m𝐻1=u. [𝑏0 𝑏1 𝑏2 𝑏3 𝑏4] =[𝑢0 𝑢1 𝑢2 𝑢3 𝑢4] ❑ The above relation between b and u leads to the following equations: 𝑏0+𝑏1+𝑏4 = 𝑢𝑜 𝑏0+ 𝑏2+ 𝑏3 = 𝑢1 𝑏1+ 𝑏3+ 𝑏4 = 𝑢2 𝑏0+ 𝑏2+ 𝑏4 = 𝑢3 𝑏1+ 𝑏2+ 𝑏3 = 𝑢4

Low density parity check(LDPC) codes ❑ Solving the above equations, we obtain: 𝑏0=𝑢2+𝑢3+𝑢4 𝑏1=𝑢1+𝑢2+𝑢3 𝑏2=𝑢0+𝑢1+𝑢2 𝑏3=𝑢0+𝑢3+𝑢4 𝑏4=𝑢0+𝑢1+𝑢4 ❑ Since b=u𝐻1 −1 . ❑ the above equations can be write in matrix form ads:

Low density parity check(LDPC) codes b = [u] thus, 𝐻1 −1 = 𝐻2 𝐻1 −1 = =

Low density parity check(LDPC) codes ❑ The generator matrix: G=[𝐻2 𝐻1 −1 𝐼𝑘]. G= ❑ The codeword can be generated as C=mG. C=[1 0 0 0 1] =[1 0 0 1 0 1 0 0 0 1].

Low density parity check(LDPC) codes 2.Efficient Encoding of LDPC Codes ❑ The preprocessing method has a complexity of O(𝑛2). ❑ LDPC code can be encoded using the parity-check matrix directly by using the efficient encoding method which has a complexity of O(n). ❑ The stepwise procedure of efficient coding of LDPC coding is as follows: Step 1:By performing row and column permutations, the nonsingular parity check matrix H is to be brought into a lower triangular form indicated in Fig. More precisely, the H matrix is brought into the form

Low density parity check(LDPC) codes 𝐻𝑡= with a gap length g as small as possible. ❑ Where A is (m − g)×(n − m) matrix, B is (m − g)×g matrix, T is (m − g)×(m − g) matrix, C is g × (n − m) matrix, D is g × g matrix and E is g × (m − g)matrix. All of these matrices are sparse and T is lower triangular with ones along the diagonal. The parity-check matrix in approximate lower triangular form

Low density parity check(LDPC) codes Step 2: Premultiply 𝐻𝑡 by: 𝐻𝑡= = ❑ In order to check that −𝐸𝑇−1𝐵 + 𝐷 is nonsingular. It is to be ensured by performing column permutations further.

Low density parity check(LDPC) codes Step 3: Obtain 𝑝1 using the following: 𝐻𝐶𝑇=0,from this equation get 𝑝1. 𝑝1 𝑇 =−𝑑−1 (−𝐸𝑇−1 𝐴 + 𝐶)𝑠𝑇 Where d=−𝐸𝑇−1𝐵 + 𝐷 and s is message vector. Step 4: Obtain 𝑝2 using the following: 𝑝2 𝑇 =−𝑇−1(A𝑠𝑇+B𝑝1 𝑇 ) Step 5: Form the code vector c as: c = [s p1 p2] 𝑝1 holds the first g parity and 𝑝2 contains the remaining parity bits.

Low Density Parity Check code THANK YOU!

coding.pdf

More Related Content

Similar to coding.pdf

Recently uploaded

coding.pdf