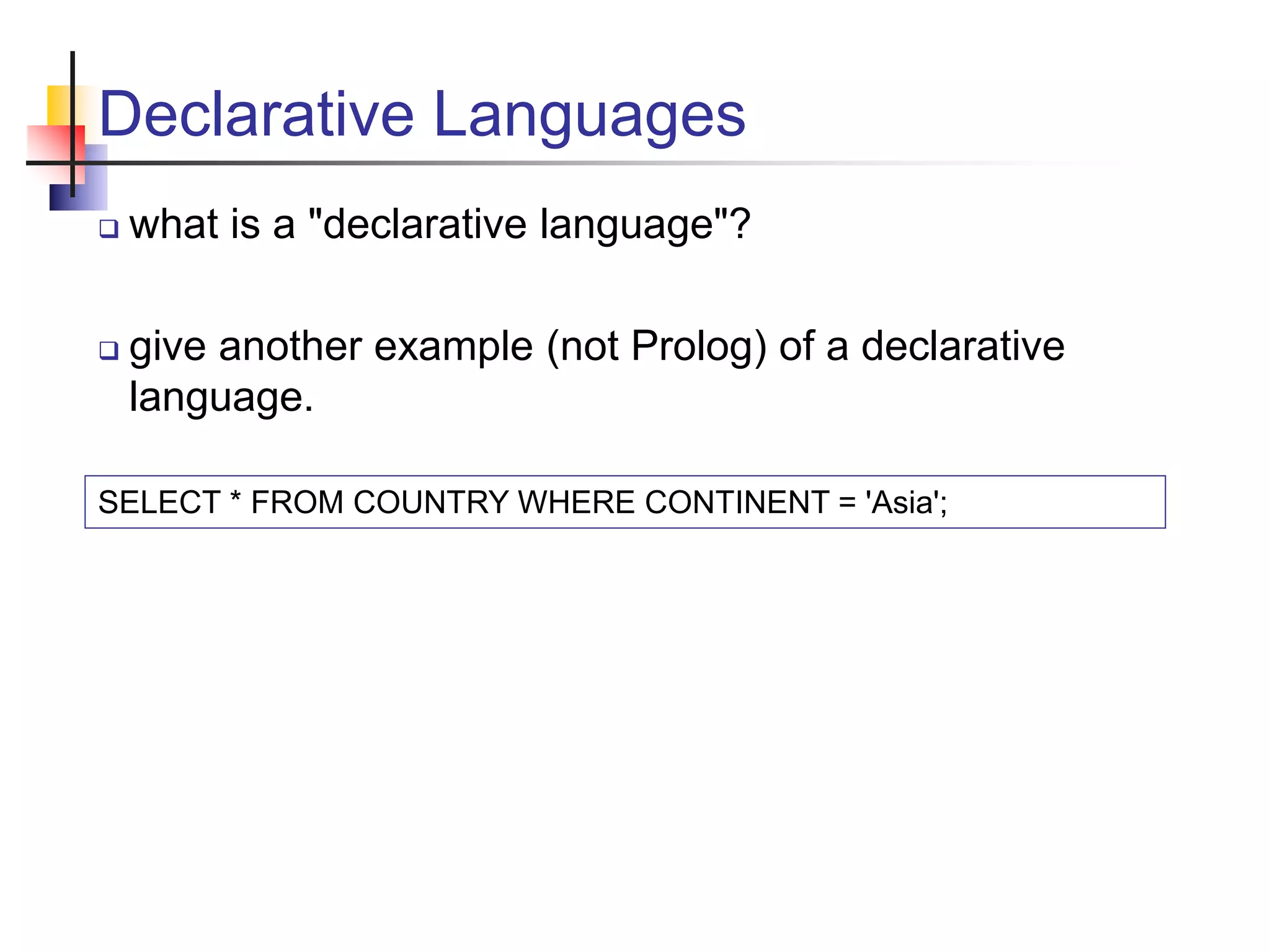
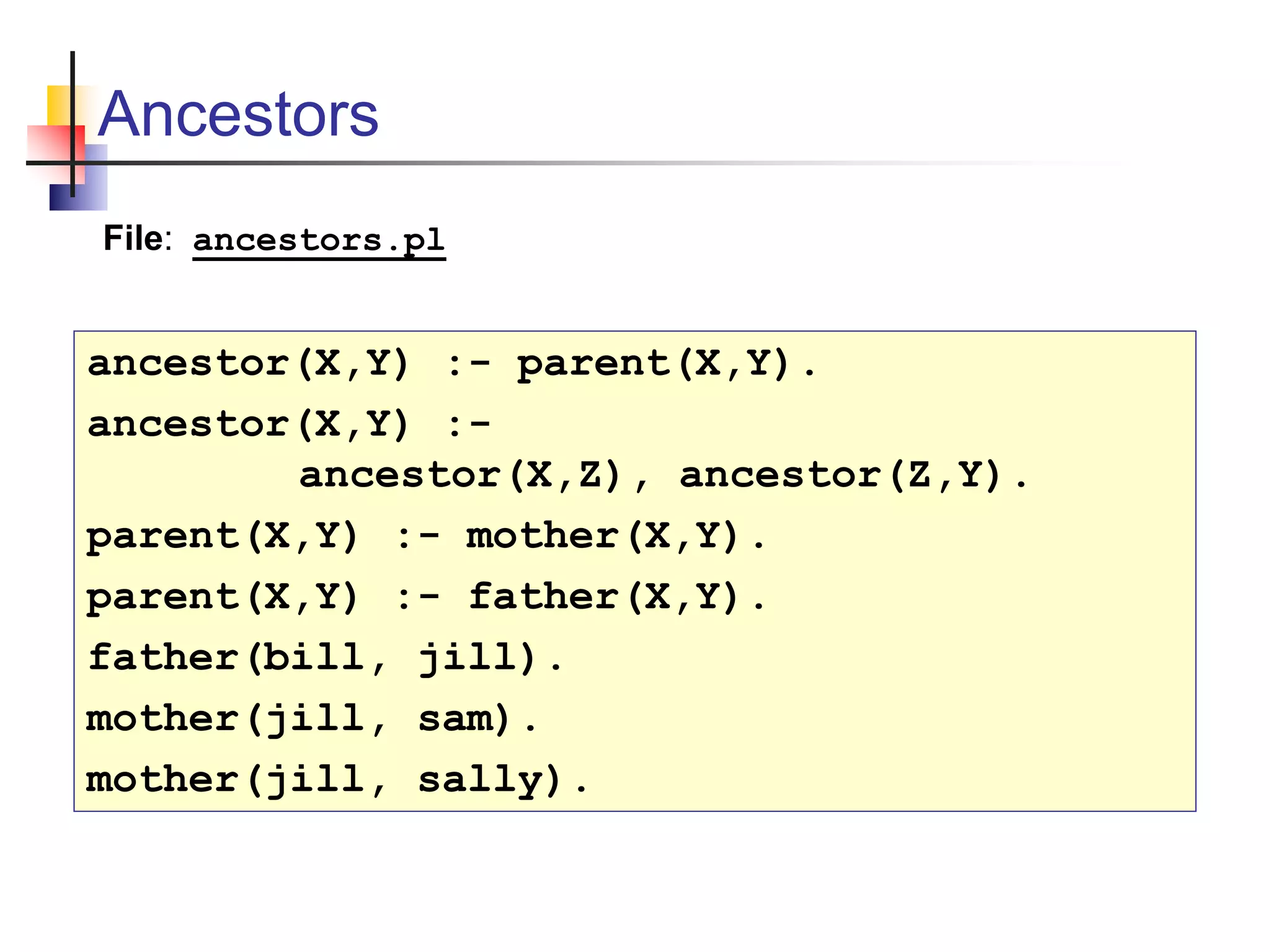
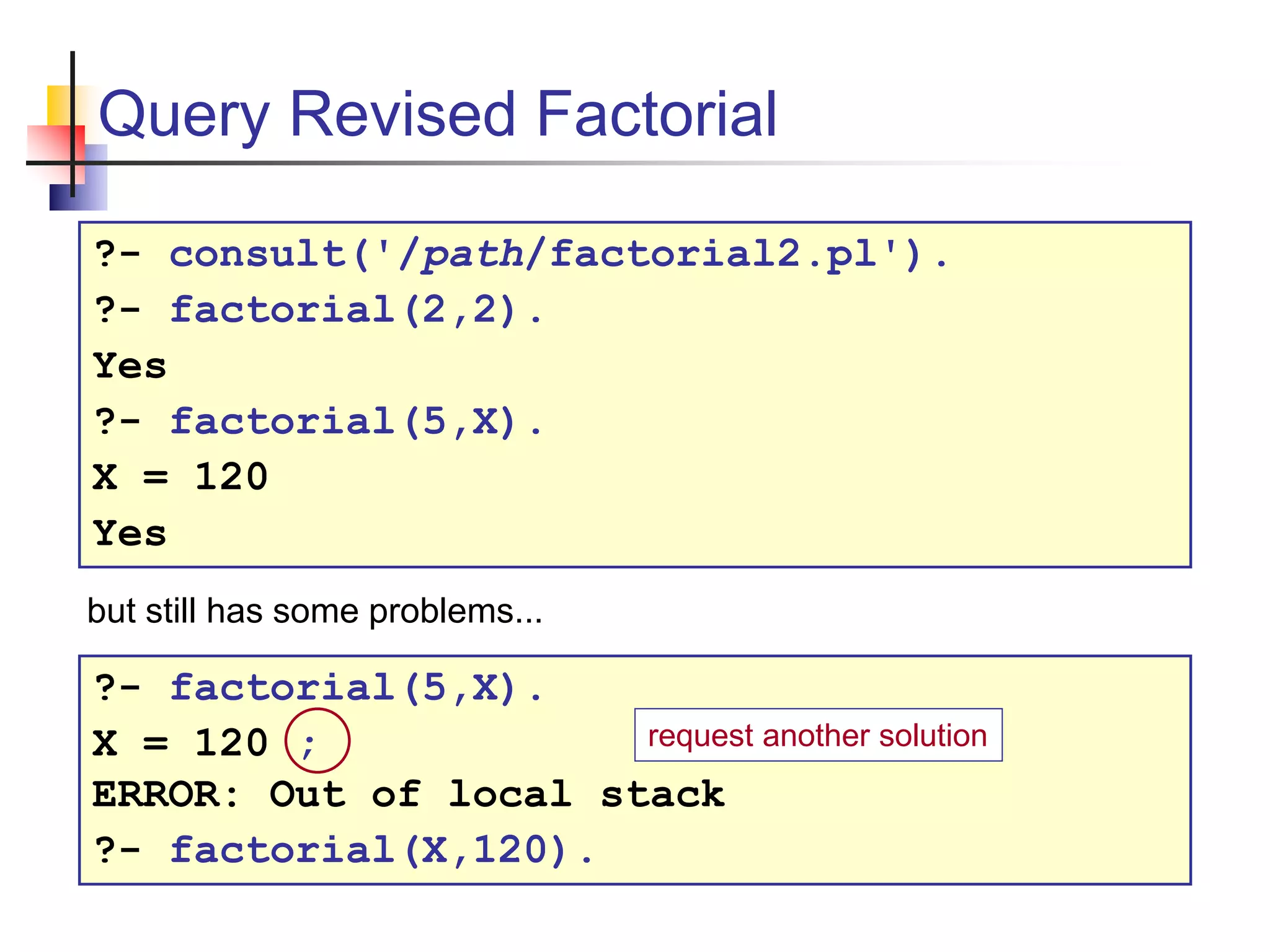
This document provides an overview of logic programming and the logic programming language Prolog. It discusses declarative programming and how Prolog uses declarative rules, facts, and predicates. It explains how Prolog performs logical operations like unification and resolution to evaluate queries against its knowledge base. It provides examples of using Prolog to represent graphs, lists, arithmetic, and more.






























![List Processing [Head | Tail] works like "car" and "cdr" in Scheme. Example: ?- [H | T ] = [a,b,c,d,e]. returns: H = a T = [b,c,d,e] This can be used to build lists and decompose lists. Can use [H|T] on the left side to de/construct a list: path(X, Y, [X|P]) :- edge(X, Node), path(Node, Y, P).](https://image.slidesharecdn.com/09logic-programming-211203090745/75/09-logic-programming-38-2048.jpg)
![member Predicate Test whether something is a member of a list ?- member(a, [b,c,d]). No. can be used to have Prolog try all values of a list as values of a variable. ?- member(X, [a1,b2,c3,d4] ). X = a1 X = b2 X = c3](https://image.slidesharecdn.com/09logic-programming-211203090745/75/09-logic-programming-39-2048.jpg)
![member Predicate example Use member to try all values of a list. Useful for problems like Queen safety enumerating possible rows and columns in a game. % dumb function to find square root of 9 squareroot9(N) :- member(N,[1,2,3,4,5,5,6,7,8,9]), 9 is N*N.](https://image.slidesharecdn.com/09logic-programming-211203090745/75/09-logic-programming-40-2048.jpg)
![appending Lists ?- append([a,b],[c,d,e],L). L = [a,b,c,d,e] append can resolve other parameters, too: ?- append(X, [b,c,d], [a,b,c,d] ). X = a ?- append([],[a,b,c],L). L = [a,b,c]](https://image.slidesharecdn.com/09logic-programming-211203090745/75/09-logic-programming-41-2048.jpg)
![Defining your own 'append' append([], List, List). append([Head|Tail], X, [Head|NewTail]) :- append(Tail, X, NewTail).](https://image.slidesharecdn.com/09logic-programming-211203090745/75/09-logic-programming-42-2048.jpg)

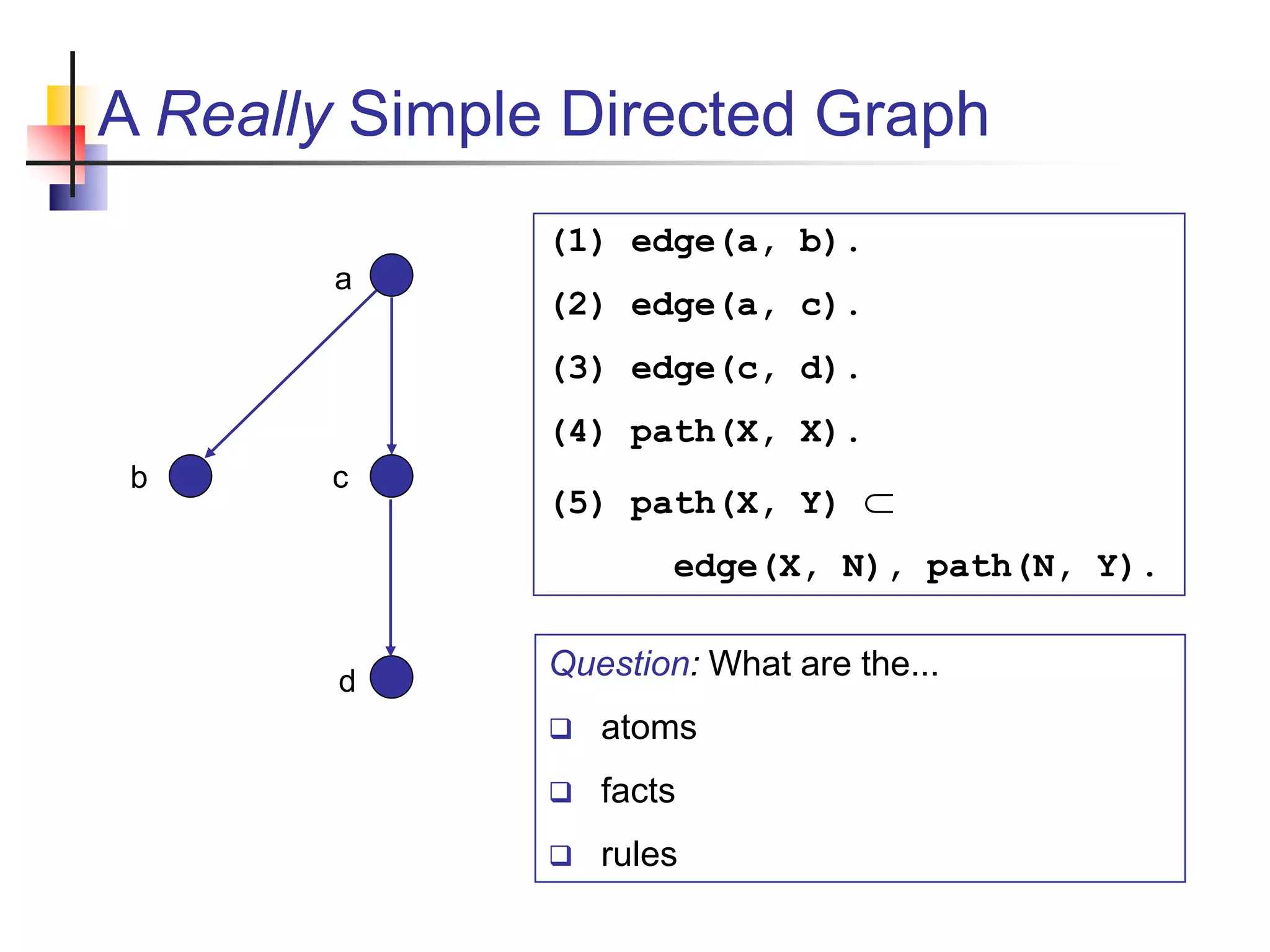
![Tracing the Solution ?- trace. [trace] ?- path(a,d). Call: (8) path(a, d) ? creep Call: (9) edge(a, _L169) ? creep Exit: (9) edge(a, b) ? creep Call: (9) path(b, d) ? creep Call: (10) edge(b, _L204) ? creep Exit: (10) edge(b, c) ? creep Call: (10) path(c, d) ? creep Call: (11) edge(c, _L239) ? creep ^ Call: (12) not(c=_G471) ? creep ^ Fail: (12) not(c=_G471) ? creep Fail: (11) edge(c, _L239) ? creep Fail: (10) path(c, d) ? creep Redo: (10) edge(b, _L204) ? creep](https://image.slidesharecdn.com/09logic-programming-211203090745/75/09-logic-programming-44-2048.jpg)
![Solution Process Stack Substitution (Instantiation) [path(a,c), path(X,X)] [path(a,c), path(a,a)] X = a Undo. [path(a,c), path(X,X)] [path(a,c), path(c,c)] X = c Undo. (1) path(X,X). (2) path(X,Y) := edge(X,Z), path(Z,Y). ?- path(a,c).](https://image.slidesharecdn.com/09logic-programming-211203090745/75/09-logic-programming-45-2048.jpg)
![Solution Process (2) Stack Substitution (Instantiation) [path(a,c), path(X,Y)] (Rule 2) [path(a,c), path(a,Y)] X = a X = a, Y = c edge(a,Z), path(Z,c) new subgoals edge(a,b), path(b,c) X = a, Y = c, Z = b path(b,c) edge(a,b) is a fact - pop it. (1) path(X,X). (2) path(X,Y) := edge(X,Z), path(Z,Y). ?- path(a,c).](https://image.slidesharecdn.com/09logic-programming-211203090745/75/09-logic-programming-46-2048.jpg)
![What does this do? % what does this do? sub([], List). sub([H|T], List) :- member(H, List), sub(T, List).](https://image.slidesharecdn.com/09logic-programming-211203090745/75/09-logic-programming-47-2048.jpg)
![What does this do? % what does this do? foo([], _, []). foo([H|T], List, [H|P]) :- member(H, List), foo(T, List, P). foo([H|T], List, P) :- not( member(H, List) ), foo(T, List, P). Underscore (_) means "don't care". It accepts any value.](https://image.slidesharecdn.com/09logic-programming-211203090745/75/09-logic-programming-48-2048.jpg)
![Max Function Write a Prolog program to find the max of a list of numbers: max( List, X). max( [3, 5, 8, -4, 6], X). X = 8. Strategy: use recursion divide the list into a Head and Tail. compare X to Head and Tail. Two cases: Head = max( Tail ). in this case answer is X is Head. X = max( Tail ) and Head < X. what is the base case?](https://image.slidesharecdn.com/09logic-programming-211203090745/75/09-logic-programming-49-2048.jpg)
![Max Function % max(List, X) : X is max of List members max([X], X). base case max([H|Tail], H) :- 1st element is max max(Tail, X), H >= X. max([H|Tail], X) :- 1st element not max complete this case.](https://image.slidesharecdn.com/09logic-programming-211203090745/75/09-logic-programming-50-2048.jpg)

