Data Structures and Algorithms
Analysis of Algorithms
Acknowledgement
The contents of these slides have origin from
School of Computing, National University of
Singapore.
We greatly appreciate support from Mr. Aaron
Tan Tuck Choy, and Dr. Low Kok Lim for
kindly sharing these materials.
2
Policies for students
These contents are only used for students
PERSONALLY.
Students are NOT allowed to modify or
deliver these contents to anywhere or anyone
for any purpose.
3
Objectives
• To introduce the theoretical basis for
1 measuring the efficiency of algorithms
• To learn how to use such measure to
compare the efficiency of different
2 algorithms
[501043 Lecture 11: Analysis of Algorithms]
4
References
Book
• Chapter 10: Algorithm Efficiency
and Sorting, pages 529 to 541.
[501043 Lecture 11: Analysis of Algorithms]
5
Outline
1. What is an Algorithm?
2. What do we mean by Analysis of
Algorithms?
3. Algorithm Growth Rates
4. Big-O notation – Upper Bound
5. How to find the complexity of a program?
6. Some experiments
7. Equalities used in analysis of algorithms
[501043 Lecture 11: Analysis of Algorithms]
6
You are expected to know…
Proof by induction
Operations on logarithm function
Arithmetic and geometric progressions
Their sums
Linear, quadratic, cubic, polynomial
functions
ceiling, floor, absolute value
[501043 Lecture 11: Analysis of Algorithms]
7
1 What is an algorithm?
1 Algorithm
A step-by-step procedure for solving a problem.
Properties of an algorithm:
Each step of an algorithm must be exact.
An algorithm must terminate.
An algorithm must be effective.
An algorithm should be general.
Terminat
Exact
e
Effective General
[501043 Lecture 11: Analysis of Algorithms]
9
2 What do we mean by Analysis
of Algorithms?
2.1 What is Analysis of Algorithms?
Analysis of algorithms
Provides tools for contrasting the efficiency of different
methods of solution (rather than programs)
Complexity of algorithms
A comparison of algorithms
Should focus on significant differences in the efficiency
of the algorithms
Should not consider reductions in computing costs
due to clever coding tricks. Tricks may reduce the
readability of an algorithm.
[501043 Lecture 11: Analysis of Algorithms]
11
2.2 Determining the Efficiency of
Algorithms
To evaluate rigorously the resources (time and
space) needed by an algorithm and represent
the result of the analysis with a formula
We will emphasize more on the time
requirement rather than space requirement here
The time requirement of an algorithm is also
called its time complexity
[501043 Lecture 11: Analysis of Algorithms]
12
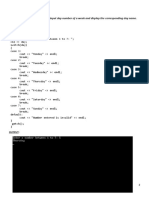
2.3 By measuring the run time?
TimeTest.java
public class TimeTest {
public static void main(String[] args) {
long startTime = System.currentTimeMillis();
long total = 0;
for (int i = 0; i < 10000000; i++) {
total += i;
}
long stopTime = System.currentTimeMillis();
long elapsedTime = stopTime - startTime;
System.out.println(elapsedTime);
}
}
Note: The run time depends on the compiler, the computer
used, and the current work load of the computer.
[501043 Lecture 11: Analysis of Algorithms]
13
2.4 Exact run time is not always needed
Using exact run time is not meaningful
when we want to compare two algorithms
coded in different languages,
using different data sets, or
running on different computers.
[501043 Lecture 11: Analysis of Algorithms]
14
2.5 Determining the Efficiency of
Algorithms
Difficulties with comparing programs instead of
algorithms
How are the algorithms coded?
Which compiler is used?
What computer should you use?
What data should the programs use?
Algorithm analysis should be independent of
Specific implementations
Compilers and their optimizers
Computers
Data
[501043 Lecture 11: Analysis of Algorithms]
15
2.6 Execution Time of Algorithms
Instead of working out the exact timing, we count
the number of some or all of the primitive
operations (e.g. +, -, *, /, assignment, …)
needed.
Counting an algorithm's operations is a way to
assess its efficiency
An algorithm’s execution time is related to the number
of operations it requires.
Examples
Traversal of a linked list
Towers of Hanoi
Nested Loops
[501043 Lecture 11: Analysis of Algorithms]
16
3 Algorithm Growth Rates
3.1 Algorithm Growth Rates (1/2)
An algorithm’s time requirements can be
measured as a function of the problem size, say n
An algorithm’s growth rate
Enables the comparison of one algorithm with another
Examples
Algorithm A requires time proportional to n2
Algorithm B requires time proportional to n
Algorithm efficiency is typically a concern for large
problems only. Why?
[501043 Lecture 11: Analysis of Algorithms]
18
3.1 Algorithm Growth Rates (2/2)
Problem size
Figure - Time requirements as a function of the problem size n
[501043 Lecture 11: Analysis of Algorithms]
19
3.2 Computation cost of an algorithm
How many operations are required?
for (int i=1; i<=n; i++) {
perform 100 operations; // A
for (int j=1; j<=n; j++) {
perform 2 operations; // B
}
}
Total Ops = A + B
[501043 Lecture 11: Analysis of Algorithms]
20
3.3 Counting the number of statements
To simplify the counting further, we can ignore
the different types of operations, and
different number of operations in a statement,
and simply count the number of statements
executed.
So, total number of statements executed in the
previous example is
[501043 Lecture 11: Analysis of Algorithms]
21
3.4 Approximation of analysis results
Very often, we are interested only in using a
simple term to indicate how efficient an algorithm
is. The exact formula of an algorithm’s
performance is not really needed.
Example:
Given the formula: 3n2 + 2n + log n + 1/(4n)
the dominating term 3n2 can tell us approximately how
the algorithm performs.
What kind of approximation of the analysis of
algorithms do we need?
[501043 Lecture 11: Analysis of Algorithms]
22
3.5 Asymptotic analysis
Asymptotic analysis is an analysis of algorithms
that focuses on
analyzing the problems of large input size,
considering only the leading term of the formula, and
ignoring the coefficient of the leading term
Some notations are needed in asymptotic
analysis
[501043 Lecture 11: Analysis of Algorithms]
23
4 Big O notation
4.1 Definition
Given a function f(n), we say g(n) is an (asymptotic)
upper bound of f(n), denoted as f(n) = O(g(n)), if there
exist a constant c > 0, and a positive integer n0 such
that f(n) c*g(n) for all n n0.
f(n) is said to be
bounded from c*g(n)
above by g(n).
O() is called the f(n)
“big O” notation.
g(n)
n0
[501043 Lecture 11: Analysis of Algorithms]
25
O(1)
O(logn)
O(n)
O(nlogn)
O(n^2)
O(n^3)
O(2^n)
Độ phức tạp nó phải rơi vào các hàm này
26
O(1): câu lệnh gán, điều kiện, công thức tính
toán
Quy tắc cộng: dành cho những câu lệnh cùng
cấp, độ phức tạp của nó là giá trị max.
Quy tắc nhân: dành cho những khối lệnh
lồng với nhau
27
4.2 Ignore the coefficients of all terms
Based on the definition, 2n2 and 30n2 have the
same upper bound n2, i.e.,
2n2 = O(n2)
Why?
30n2 = O(n2)
They differ only in the choice of c.
Therefore, in big O notation, we can omit the
coefficients of all terms in a formula:
Example: f(n) = 2n2 + 100n = O(n2) + O(n)
[501043 Lecture 11: Analysis of Algorithms]
28
4.3 Finding the constants c and n0
Given f(n) = 2n2 + 100n, prove that f(n) = O(n2).
Observe that: 2n2 + 100n 2n2 + n2 = 3n2
whenever n ≥ 100.
Set the constants to be c = 3 and n0 = 100.
By definition, we have f(n) = O(n2).
Notes:
1. n2 2n2 + 100n for all n, i.e., g(n) f(n), and yet g(n)
is an asymptotic upper bound of f(n)
2. c and n0 are not unique.
For example, we can choose c = 2 + 100 = 102, and
n0 = 1 (because f(n) 102n2 n ≥ 1)
Q: Can we write f(n) = O(n3)?
[501043 Lecture 11: Analysis of Algorithms]
29
4.4 Is the bound tight?
The complexity of an algorithm can be bounded
by many functions.
Example:
Let f(n) = 2n2 + 100n.
f(n) is bounded by n2, n3, n4 and many others according
to the definition of big O notation.
Hence, the following are all correct:
f(n) = O(n2); f(n) = O(n3); f(n) = O(n4)
However, we are more interested in the tightest
bound which is n2 for this case.
[501043 Lecture 11: Analysis of Algorithms]
30
4.5 Growth Terms: Order-of-Magnitude
In asymptotic analysis, a formula can be simplified
to a single term with coefficient 1
Such a term is called a growth term (rate of
growth, order of growth, order-of-magnitude)
The most common growth terms can be ordered
as follows: (note: many others are not shown)
O(1) < O(log n) < O(n) < O(n log n) < O(n2) < O(n3) < O(2n) < …
“fastest” “slowest”
Note:
“log” = log base 2, or log2; “log10” = log base 10; “ln” = log
base e. In big O, all these log functions are the same.
(Why?)
[501043 Lecture 11: Analysis of Algorithms]
31
4.6 Examples on big O notation
f1(n) = ½n + 4
= O(n)
f2(n) = 240n + 0.001n2
= O(n2)
f3(n) = n log n + log n + n log (log n)
= O(n log n)
Why?
[501043 Lecture 11: Analysis of Algorithms]
32
4.7 Exponential Time Algorithms
Suppose we have a problem that, for an input
consisting of n items, can be solved by going
through 2n cases
We say the complexity is exponential time
Q: What sort of problems?
We use a supercomputer that analyses 200
million cases per second
Input with 15 items, 164 microseconds
Input with 30 items, 5.36 seconds
Input with 50 items, more than two months
Input with 80 items, 191 million years!
[501043 Lecture 11: Analysis of Algorithms]
33
4.8 Quadratic Time Algorithms
Suppose solving the same problem with another
algorithm will use 300n2 clock cycles on a 80386,
running at 33MHz (very slow old PC)
We say the complexity is quadratic time
Input with 15 items, 2 milliseconds
Input with 30 items, 8 milliseconds
Input with 50 items, 22 milliseconds
Input with 80 items, 58 milliseconds
What observations do you have from the results of these
two algorithms? What if the supercomputer speed is
increased by 1000 times?
It is very important to use an efficient algorithm to solve a
problem
[501043 Lecture 11: Analysis of Algorithms]
34
4.9 Order-of-Magnitude Analysis and Big
O Notation (1/2)
Figure - Comparison of growth-rate functions in tabular form
[501043 Lecture 11: Analysis of Algorithms]
35
4.9 Order-of-Magnitude Analysis and Big
O Notation (2/2)
Figure - Comparison of growth-rate functions in graphical form
[501043 Lecture 11: Analysis of Algorithms]
36
4.10 Example: Moore’s Law
Intel co-founder Gordon
Moore is a visionary. In
1965, his prediction,
popularly known as Moore's
Law, states that the number
of transistors per square
inch on an integrated circuit
chip will be increased
exponentially, double about
every two years. Intel has
kept that pace for nearly 40
years.
[501043 Lecture 11: Analysis of Algorithms]
37
4.11 Summary: Order-of-Magnitude
Analysis and Big O Notation
Order of growth of some common functions:
O(1) < O(log n) < O(n) < O(n log n) < O(n2) < O(n3) < O(2n) < …
Properties of growth-rate functions
You can ignore low-order terms
You can ignore a multiplicative constant in the high-
order term
O(f(n)) + O(g(n)) = O( f(n) + g(n) )
[501043 Lecture 11: Analysis of Algorithms]
38
5 How to find the complexity of
a program?
5.1 Some rules of thumb and examples
Basically just count the number of statements executed.
If there are only a small number of simple statements in a
program – O(1)
If there is a ‘for’ loop dictated by a loop index that goes up
to n – O(n)
If there is a nested ‘for’ loop with outer one controlled by n
and the inner one controlled by m – O(n*m)
For a loop with a range of values n, and each iteration
reduces the range by a fixed constant fraction (eg: ½)
– O(log n)
For a recursive method, each call is usually O(1). So
if n calls are made – O(n)
if n log n calls are made – O(n log n)
[501043 Lecture 11: Analysis of Algorithms]
40
5.2 Examples on finding complexity (1/2)
What is the complexity of the following code fragment?
int sum = 0;
for (int i=1; i<n; i=i*2) {
sum++;
}
It is clear that sum is incremented only when
i = 1, 2, 4, 8, …, 2k where k = log2 n
There are k+1 iterations. So the complexity is O(k) or
O(log n)
Note:
In Computer Science, log n means log2 n.
When 2 is replaced by 10 in the ‘for’ loop, the complexity is O(log10 n)
which is the same as O(log2 n). (Why?)
log10 n = log2 n / log2 10
[501043 Lecture 11: Analysis of Algorithms]
41
5.2 Examples on finding complexity (2/2)
What is the complexity of the following code fragment?
(For simplicity, let’s assume that n is some power of 3.)
int sum = 0;
for (int i=1; i<n; i=i*3) {
for (j=1; j<=i; j++) {
sum++;
}
}
f(n) = 1 + 3 + 9 + 27 + … + 3(log3 n)
= 1 + 3 + … + n/9 + n/3 + n
= n + n/3 + n/9 + … + 3 + 1 (reversing the terms in previous step)
= n * (1 + 1/3 + 1/9 + …)
n * (3/2)
Why is (1 + 1/3 + 1/9 + …) 3/2?
= 3n/2
See slide 56.
= O(n)
[501043 Lecture 11: Analysis of Algorithms]
42
5.3 Eg: Analysis of Tower of Hanoi
Number of moves made by the algorithm is
n
2 – 1. Prove it!
Hints: f(1)=1, f(n)=f(n-1) + 1 + f(n-1), and prove by
induction
Assume each move takes t time, then:
f(n) = t * (2n-1) = O(2n).
The Tower of Hanoi algorithm is an exponential
time algorithm.
[501043 Lecture 11: Analysis of Algorithms]
43
5.4 Eg: Analysis of Sequential Search (1/2)
Check whether an item x is in an unsorted
array a[]
If found, it returns position of x in array
If not found, it returns -1
public int seqSearch(int[] a, int len, int x)
{
for (int i = 0; i < len; i++) {
if (a[i] == x)
return i;
}
return -1;
}
[501043 Lecture 11: Analysis of Algorithms]
44
5.4 Eg: Analysis of Sequential Search (2/2)
Time spent in each iteration through the loop is at most
some constant t1
Time spent outside the loop is at most some constant t2
Maximum number of iterations is n, the length of the array
Hence, the asymptotic upper bound is:
t1 n + t2 = O(n) public int seqSearch(int[] a,
int len, int x) {
for (int i = 0; i < len; i++) {
Rule of Thumb: if (a[i] == x)
In general, a loop of n return i;
iterations will lead to O(n) }
return -1;
growth rate (linear complexity). }
[501043 Lecture 11: Analysis of Algorithms]
45
5.5 Eg: Binary Search Algorithm
Requires array to be sorted in ascending order
Maintain subarray where x (the search key) might
be located
Repeatedly compare x with m, the middle element
of current subarray
If x = m, found it!
If x > m, continue search in subarray after m
If x < m, continue search in subarray before m
[501043 Lecture 11: Analysis of Algorithms]
46
5.6 Eg: Non-recursive Binary Search (1/2)
Data in the array a[] are sorted in ascending order
public static int binSearch(int[] a, int len, int
x) {
int mid, low = 0;
int high = len - 1;
while (low <= high) {
mid = (low + high) / 2;
if (x == a[mid]) return mid;
else if (x > a[mid]) low = mid + 1;
else high = mid - 1;
}
return -1;
}
[501043 Lecture 11: Analysis of Algorithms]
47
5.6 Eg: Non-recursive Binary Search (2/2)
Time spent outside the loop is at most t1
Time spent in each iteration of the loop is at most
t2
For inputs of size n, if we go through at most f(n)
iterations, then the complexity is
t1 + t2 f(n) public static int binSearch(int[] a, int len, int x)
{
int mid, low = 0;
or O(f(n)) int high = len - 1;
while (low <= high) {
mid = (low + high) / 2;
if (x == a[mid]) return mid;
else if (x > a[mid]) low = mid + 1;
else high = mid - 1;
}
return -1;
}
[501043 Lecture 11: Analysis of Algorithms]
48
5.6 Bounding f(n), the number of iterations (1/2)
At any point during binary search, part of array is “alive”
(might contain the point x)
Each iteration of loop eliminates at least half of previously
“alive” elements
At the beginning, all n elements are “alive”, and after
After 1 iteration, at most n/2 elements are left, or alive
After 2 iterations, at most (n/2)/2 = n/4 = n/22 are left
After 3 iterations, at most (n/4)/2 = n/8 = n/23 are left
:
After i iterations, at most n/2i are left
At the final iteration, at most 1 element is left
[501043 Lecture 11: Analysis of Algorithms]
49
5.6 Bounding f(n), the number of iterations (2/2)
In the worst case, we have to search all the way up to the
last iteration k with only one element left.
We have:
n/2k = 1
2k = n
k = log n
Hence, the binary search algorithm takes O(f(n)) , or O(log n)
times
Rule of Thumb:
In general, when the domain of interest is reduced by a
fraction (eg. by 1/2, 1/3, 1/10, etc.) for each iteration of a
loop, then it will lead to O(log n) growth rate.
The complexity is log n.
2
[501043 Lecture 11: Analysis of Algorithms]
50
5.6 Analysis of Different Cases
Worst-Case Analysis
Interested in the worst-case behaviour.
A determination of the maximum amount of time that an algorithm
requires to solve problems of size n
Best-Case Analysis
Interested in the best-case behaviour
Not useful
Average-Case Analysis
A determination of the average amount of time that an algorithm
requires to solve problems of size n
Have to know the probability distribution
The hardest
[501043 Lecture 11: Analysis of Algorithms]
51
5.7 The Efficiency of Searching Algorithms
Example: Efficiency of Sequential Search (data not
sorted)
Worst case: O(n)
Which case?
Average case: O(n)
Best case: O(1)
Why? Which case?
Unsuccessful search?
Q: What is the best case complexity of Binary Search
(data sorted)?
Best case complexity is not interesting. Why?
[501043 Lecture 11: Analysis of Algorithms]
52
5.8 Keeping Your Perspective
If the problem size is always small, you can
probably ignore an algorithm’s efficiency
Weigh the trade-offs between an algorithm’s
time requirements and its memory requirements
Compare algorithms for both style and efficiency
Order-of-magnitude analysis focuses on large
problems
There are other measures, such as big Omega (), big
theta (), little oh (o), and little omega (). These may be
covered in more advanced module.
[501043 Lecture 11: Analysis of Algorithms]
53
6 Some experiments
6.1 Compare Running Times (1/3)
We will compare a single loop, a double nested
loop, and a triply nested loop
See CompareRunningTimes1.java,
CompareRunningTimes2.java, and
CompareRunningTimes3.java
Run the program on different values of n
[501043 Lecture 11: Analysis of Algorithms]
55
6.1 Compare Running Times (2/3)
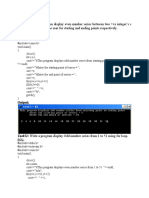
CompareRunningTimes1.java
System.out.print("Enter problem size n: ");
int n = sc.nextInt();
long startTime = System.currentTimeMillis();
int x = 0;
// Single loop
for (int i=0; i<n; i++) {
x++;
}
long stopTime = System.currentTimeMillis();
long elapsedTime = stopTime - startTime;
CompareRunningTimes2.java CompareRunningTimes3.java
int x = 0;
int x = 0; // Triply nested loop
// Doubly nested loop for (int i=0; i<n; i++) {
for (int i=0; i<n; i++) { for (int j=0; j<n; j++) {
for (int j=0; j<n; j++) { for (int k=0; k<n; k++) {
x++; x++;
} }
} }
[501043 Lecture 11: Analysis of Algorithms] } 56
6.1 Compare Running Times (3/3)
Single Doubly Triply
n loop nested Ratio nested Ratio
O(n) loop O(n2) loop O(n3)
100 0 2 29
200 0 7 7/2 = 3.5 131 131/29 = 4.52
400 0 12 12/7 = 1.71 960 7.33
800 0 17 17/12 = 1.42 7506 7.82
1600 0 38 38/17 = 2.24 59950 7.99
3200 1 124 124/38 = 3.26 478959 7.99
6400 1 466 3.76
12800 2 1844 3.96
25600 4 7329 3.97
51200 8 29288 4.00
[501043 Lecture 11: Analysis of Algorithms]
57
7 Equalities used in analysis of
algorithms
7.1 Formulas
Some common formulas used in the analysis of
algorithm is on the 501043 “Lectures” website
http://sakai.it.tdt.edu.vn
For example, in slide 39, to show
(1 + 1/3 + 1/9 + …) 3/2
We use this formula
For a geometric progression ,
If 0 < c < 1, then the sum of the infinite geometric series is
… (5)
ai = 1; c = 1/3
Hence sum = 1/(1 – 1/3) = 3/2
[501043 Lecture 11: Analysis of Algorithms]
59
End of file