MACHINE LEARNING ACCELERATOR

Tabular Data – Lecture 3

Course Overview
Lecture 1 Lecture 2 Lecture 3

• Introduction to ML • Feature Engineering • Optimization

• Model Evaluation • Tree-based Models • Regression Models

 Train-Validation-Test  Decision Tree • Regularization

 Overfitting  Random Forest • Boosting

• Exploratory Data Analysis • Hyperparameter Tuning • Neural Networks

• K Nearest Neighbors (KNN) • AWS AI/ML Services • AutoML

Optimization
Optimization in Machine Learning
• We build and train ML models, hoping for:

ML Model Features ML Model (Rules) ML Model Target

• In reality … error

ML Model Features ML Model (Rules) ML Model Prediction

• Learn better and better models, such that overall model error gets smaller
and smaller … ideally, as small as possible!
Optimization
• In ML, use optimization to minimize an error function of the ML model
 Error function: , where = input, = function, = output
 Optimizing the error function:
- Minimizing means finding the input that results in the lowest value
- Maximizing, means finding that gives the largest
Gradient Optimization
• Gradient: direction and rate of the fastest increase of a function.
 It can be calculated with partial derivatives of the function with respect
to each input variable in .
 Because it has a direction, the gradient is a “vector”.
Gradient Example
, with gradient vector
• Sign of the gradient shows direction the
function increases: + right and – left
Gradient Example
, with gradient vector
• Sign of the gradient shows direction the
function increases: + right and – left
Gradient Example
, with gradient vector
• Sign of the gradient shows direction the
function increases: + right and – left

• As we go towards to the bottom part of the

function, gradient gets smaller
Gradient Example
, with gradient vector
• Sign of the gradient shows direction the
function increases: + right and – left

• As we go towards to the bottom part of the

function, gradient gets smaller and becomes zero
(i.e., function can no longer change, can no longer
decrease – it reached the min!)
Gradient Descent Method
• Gradient Descent method uses gradients to find the minimum of a
function iteratively.
• Taking steps (proportional to the gradient size) towards the minimum, in
the opposite direction of the gradient.

• Gradient Descent Algorithm:

 Start at an initial point
 Update:
Gradient Descent Method

large Initial Values large

Global Minimum
Regression Models
Linear Regression
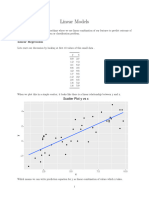
We use (linear) regression for
numerical value prediction.
Example: How does the price of a
house (target, outcome , ) change
relate to its square footage living
(feature, attribute )?

* Data source: King County, WA Housing Info. For ,

Multiple Linear Regression
Example: How does the price of a house (target, outcome ) change relate
to its square footage living (feature ), its number of bedrooms (feature
), its zip code ( ),…? That is, using multiple features…

Using the multiple linear regression equation:

• Assuming all other variables stay the same, an increase of by 1 foot
square, increases the price by
• Assuming all other variables stay the same, an increase of by 1
bedroom, increases the price by , and so on …
Linear Regression
Regression line , is
defined by: (intercept), (slope).
The vertical offset for each data point
from the line is the error between the
true label) and (the prediction based on
).
Best “line” (best , ) minimizes the
sum of squared errors (SSE):
Fitting a Model: Gradient Descent
• For a Linear Regression model:
,

with features , and parameters/weights

• Minimize the Mean Squared Error cost function:
: index; : number of samples
: output; : model prediction

• Iteratively update parameters/weights with Gradient Descent:

From Regression to Classification
Linear regression was useful when predicting continuous values

Can we use a similar approach to solve classification problems?

The most simple classification problem is a binary classification, where {0,
1}.
Examples:
Email: Spam or Not Spam
Text: Positive or Negative product review
Image: Cat or Not Cat
Logistic Regression
Idea: We can apply the Sigmoid function to
• Sigmoid (Logistic) function

“squishes” values to the 0 –1 range.

• Can define a “Decision boundary” at 0.5
- if 0.5, round down (class 0)
- if 0.5, round up (class 1)
• Our regression equation becomes:
Log-Loss (Binary Cross-Entropy)
Log-Loss: A numeric value that measures the performance of a binary
classifier when model output is a probability between 0 and 1:

: true class {0, 1}, = : probability of class, and : logarithm

• As the output of Logistic Regression is between 0 and 1, Log-Loss is a

suitable cost function for the Logistic Regression.
• To improve Logistic Regression model learning from data, minimize Log-
Loss.
Log-Loss (Binary Cross-Entropy)
Example: Let’s calculate the Log-Loss

for the following scenarios:

• : true class = 1, = 0.3

LogLoss
LogLoss
• : true class = 1, = 0.8 p=0.3
p=0.8

Better prediction gives smaller Log-Loss predicted probability

Fitting a Model: Gradient Descent
• For a Logistic Regression model:
,

with features , and parameters/weights

• Minimize the LogLoss cost function:
: index; : # samples
: output
: model prediction

• Iteratively update parameters/weights with Gradient Descent:

Regularization
Regularization
Underfitting: Model too simple, fewer features,
smaller weights, weak learning.
Overfitting: Model too complex, too many features,
larger weights, weak generalization.
‘Good Fit’ Model: Compromise between fit and
complexity (drop features, reduce weights).

Regularization does both: penalizes large weights,

sometimes reduced all the way to zero!
Regularization
• Tune model complexity by adding a penalty score for complexity to the
cost function (think error function, minimizing towards best fit!):

• Calibrate regularization strength by using a regularizer parameter,

• Standard regularization types:
 L2 regularization (Ridge): (L2: popular choice)
 L1 regularization (LASSO): (L1: useful as feature
selection, since most
 Both L2 and L1 (ElasticNet)
weights shrink to 0 -
sparsity)
• Note: Important to scale features first!
Regression in sklearn
LinearRegression: sklearn Linear Regression (and regularization)
LinearRegression()
Ridge(alpha=1.0), RidgeCV(alpha=1.0, cv=5)
Lasso(alpha=1.0), LassoCV(alpha=1.0, cv=5)
ElasticNet(alpha=1.0, l1_ratio=0.5), ElasticNetCV(cv=5)

LogisticRegression: sklearn Logistic Regression (and regularization)

LogisticRegression(penalty='l2', C=1.0, l1_ratio=None)
LogisticRegressionCV(penalty='l2', C=1.0, l1_ratio=None, cv=5)
Ensemble Methods: Boosting
Boosting
Boosting method: build multiple weak models sequentially, each
subsequent model attempting to boost performance overall, by
overcoming/reducing the errors of the previous model.
Data

Weak Model Weak Model Weak Model …

Prediction 1 Prediction 2 Prediction 2

Ensemble Prediction
Boosting
Boosting method: build multiple weak models sequentially, each
subsequent model attempting to boost performance overall, by
overcoming/reducing the errors of the previous model.

Data Data Data

Weak Model Weak Model Weak Model …

Prediction 1 Prediction 2 Prediction 3
far from target far from target far from target
Boosting
Boosting method: build multiple weak models sequentially, each
subsequent model attempting to boost performance overall, by
overcoming/reducing the errors of the previous model.

Data 1

Weak Model 1

Prediction large error

far from target

Ensemble
Prediction
Boosting
Boosting method: build multiple weak models sequentially, each
subsequent model attempting to boost performance overall, by
overcoming/reducing the errors of the previous model.

Data 1

Weak Model 1

Prediction large error

far from target

Ensemble
Prediction
Boosting
Boosting method: build multiple weak models sequentially, each
subsequent model attempting to boost performance overall, by
overcoming/reducing the errors of the previous model.

Data 1 Data 2

Weak Model 1 Weak Model 2

Prediction large error

far from target

Ensemble
Prediction
Boosting
Boosting method: build multiple weak models sequentially, each
subsequent model attempting to boost performance overall, by
overcoming/reducing the errors of the previous model.

Data 1 Data 2

Weak Model 1 Weak Model 2

Prediction large error Prediction still large error

far from target far from target

Ensemble
Prediction
Boosting
Boosting method: build multiple weak models sequentially, each
subsequent model attempting to boost performance overall, by
overcoming/reducing the errors of the previous model.

…
Data 1 Data 2

Weak Model 1 Weak Model 2 …

Prediction large error Prediction still large error …

far from target far from target

Ensemble …
Prediction
Gradient Boosting Machines (GBM)
Gradient Boosting Machines (GBM): Boosting trees
• Train a weak model on the given data, and make predictions with it
• Iteratively create a new model to learn to overcome prediction errors of the
previous model (use previous prediction error as new target)
Features Features Features Features

Target 2- Prediction 2
Target 1- Prediction 1

Target 3- Prediction 3
Target 1 Target 2 Target 3 … Target N

Tree 1 Tree 2 Tree 3 … Tree N

Prediction 1 Prediction 2 Prediction 3 … Prediction N

Prediction 1 + Prediction 2 + Prediction 3 + … + Prediction N

Gradient Boosting in Python
• sklearn GBM algorithms:
 GradientBoostingClassifier (Regressor)
 HistGradientBoostingClassifier (Regressor) – faster, experimental
• Additional third-party libraries provide computationally efficient alternate
GBM implementations, with better results in practice:
 XGBoost (Extreme Gradient Boosting): efficient compute, memory
 LightGBM: much faster
 CatBoost (Category Gradient Boosting): fast, supports categoricals
Gradient Boosting in sklearn
GradientBoostingClassifier: sklearn’s Gradient Boosting classifier
(there is also a Regressor version) - .fit(), .predict()

GradientBoostingClassifier(n_estimators=100, learning_rate = 0.1,

min_samples_split=2, min_samples_leaf=1, max_depth=3)

The full interface is larger.

Notice the mix of boosting-specific and tree-specific parameters.
Gradient Boosting in sklearn
HistGradientBoostingClassifier: sklearn’s Light GBM classifier (there
is also a Regressor version), in experimental stage - .fit(), .predict()

from sklearn.experimental import enable_hist_gradient_boosting

HistGradientBoostingClassifier(max_iter=100, learning_rate = 0.1,
max_leaf_nodes=31, min_samples_leaf=20, max_depth=None)

The full interface is larger.

Neural Networks
Looking back at Regression Models
Output Linear Regression*: Given { },
predict :

(sum)
(weights)
Input

* Basically assuming that the output depends only on

first order interactions of the inputs
Looking back at Regression Models
Output Linear Regression*: Given { },
predict :

where is the linear function:

Activation function
(sum)
(weights)
Input

* Linear activation function

Looking back at Regression Models
Output Logistic Regression*: Given { },
predict , where ::

where is the logistic function:

Activation function
(sum)
(weights)
Input

* Non-linear activation function / binary classifier

Perceptron (Rosenblatt, 1957)
Output Perceptron*: Given { }, predict ,
where :

where is the step function:

Activation function
(sum)
(weights)
Input

* Non-linear activation function / binary classifier

Artificial Neuron
Output Artificial Neuron*: Given { },
predict :

where is a nonlinear activation

function (sigmoid, tanh, ReLU, …)
Activation function
(sum)
(weights)
Input

* Similar to how neurons in the brain function

Artificial Neuron
Output
Artificial Neuron: Captures mostly
linear interactions in the data.

Question: Can we use a similar

approach to capture non-linear
Activation function
interactions in the data?
(sum)
(weights)
Input Not a very good classifier
…
Neural Network/Multilayer Perceptron
Output
Artificial Neuron: Captures mostly
linear interactions in the data.

Question: Can we use a similar

(3 weights)
approach to capture non-linear
interactions in the data?

(6 weights)
Input Much better!
Neural Network/Multilayer Perceptron
Artificial Neuron: Captures mostly
linear interactions in the data
Output Layer
Question: Can we use a similar
(3 weights)
approach to capture non-linear
Hidden Layer
interactions in the data?

(6 weights) Neural Network/Multilayer

Input Layer
Perceptron (MLP): Use more
Artificial Neurons, stack in a layer!
Neural Network/Multilayer Perceptron
• A neural network consisting of
input, hidden and output layers.
Output Layer • Each layer is connected to the next
(3 weights) layer.
Hidden Layer • An activation function is applied on
each hidden layer (and output layer).
(6 weights) • More details
Input Layer
Neural Network/Multilayer Perceptron
• A neural network consisting of
input, hidden and output layers.
Output Layer • Each layer is connected to the next
(5 weights) layer.
Hidden • An activation function is applied on
Layer
each hidden layer (and output layer).
(12 weights) • More details
Input Layer
Neural Networks

MultiLayer Network: Two layers (one hidden layer, output layer), with five
hidden neurons in the hidden layer, and one output neuron.

MultiLayer Network: Two layers (one hidden layer, output layer), with five MultiLayer Network: Four layers (three hidden layer, output layer), with five-three-
hidden neurons in the hidden layer, and three output neurons. two hidden neurons in the hidden layers, and two output neurons.

More details
Build and Train a Neural Network

𝒐
(𝒐𝒖𝒕 ) We build a neural network for a binary
Output Layer
𝒐
(𝒊𝒏) classification task, with:

• (no bias, for simplicity)

• 2 inputs: = 0.5 and = 0.1
(𝒐𝒖𝒕 )
𝒉𝟏 𝒉𝟐
(𝒐𝒖𝒕 )
Hidden Layer • 1 hidden layer with 2 neurons
(𝒊𝒏) (𝒊𝒏)
𝒉𝟏 𝒉𝟐 • 1 output neuron in the output layer

Input Layer
Activation Functions
• “How to get from linear weighted sum input to non-linear output?”
Name Plot Function Description

1
The most common activation
Logistic (sigmoid) function. Squashes input to
0 x (0,1).

Hyperbolic tangent 1
Squashes input to (-1, 1).
(tanh) 0 x
-1
Popular activation function.
Rectified Linear Unit Anything less than 0, results
(ReLU) in zero activation.
0 x
Derivatives of these functions are also important (gradient descent).
Output Activations/Functions
• “How to output/predict a result”
Problem Description Name Function

Binary • Output probability for each class, in (0,1)

classification • Logistic regression of output of last layer Sigmoid

• Output probability for each class, in (0,1)

Multi-class
• Sum of outputs to be 1 (probability distribution)
classification • Training drives target class values up, others down Softmax

Regression Linear/ ReLU

Build and Train a Neural Network

𝒐
(𝒐𝒖𝒕 ) We build a neural network for a binary
Output Layer
𝒐
(𝒊𝒏) classification task, with:

• (no bias, for simplicity)

• 2 inputs: = 0.5 and = 0.1
(𝒐𝒖𝒕 )
𝒉𝟏 𝒉𝟐
(𝒐𝒖𝒕 )
Hidden Layer • 1 hidden layer with 2 neurons
(𝒊𝒏) (𝒊𝒏)
𝒉𝟏 𝒉𝟐 • 1 output neuron in the output layer
• All neurons have sigmoid activation function:

Input Layer
Forward Pass
(𝒐𝒖𝒕 )
𝒐 Output Layer
(𝒊𝒏)
𝒐

0.4 0.45

0 . 52 0 .53 Hidden Layer

0.1 0.13
0.25 0.2

0.15 0.4 Similarly,

0.5 0.1 Input Layer
Forward Pass

0 . 61
Output Layer
0.44

0.4 0.45

0 . 52 0 .53 Hidden Layer

0.1 0.13
0.25 0.2

0.15 0.4
For binary classification, we would
0.5 0.1 Input Layer classify this (0.5, 0.1) input data point, as
class 1 (as 0.61 > 0.5).
Cost Functions
• “How to compare the outputs with the truth?”
Problem Name Function Notes

Notations for Classification

Binary Cross entropy for • = training examples
classification logistic • = classes
• = prediction (probability)
• = true class (1/yes, 0/no)
Multi-class Cross entropy for
classification Softmax
Notations for Regression
• = training examples
Regression Mean Squared • = prediction (numeric, )
Error • = true value
Training Neural Networks
• Cost function is selected according to problem: Binary, Multi-class
Classification or Regression.
• Update network weights by applying the gradient descent method and
backpropagation. More details

• Weight update formula:

: Cost
Gradient with respect to
Dropout
• Regularization technique to prevent overfitting.
• Randomly removes some nodes with a fixed probability during the
training.

More details
Why Neural Networks?
• Automatically extract useful features
from input data.
• In recent years, deep learning has
achieved state-of-the art results in
many machine learning areas.

• Three pillars of deep learning:

 Data
 Compute
 Algorithms
Build and Train Neural Networks
• How to build and use these ML models?
• Can it be this simple?
Dive into Deep Learning

E-book on Deep Learning by Amazon Scientists, available here: https://d2l.ai

Related chapters:
Chapters 3: Linear Neural Networks: https://d2l.ai/chapter_linear-networks/index.html
Chapters 4: Multilayer Perceptrons: https://d2l.ai/chapter_multilayer-perceptrons/index.html
MXNet Hands-on
• Open source Deep Learning Library to train
and deploy neural networks.
• With the Gluon interface, we can define and
train neural networks easily.

MLA-TAB-Lecture3-MXNet.ipynb
Putting it all together: Lecture 3
• In this notebook, we continue to work with our review dataset to
predict the target field
• The notebook covers the following tasks:
 Exploratory Data Analysis
 Splitting dataset into training and test sets
 Data Balancing, categoricals encoding, text vectorization
 Train a Neural Network
 Check the performance metrics on test set

MLA-TAB-Lecture3-Neural-Networks.ipynb
AutoML
AutoML
AutoML helps automating some of the tasks related to ML model
development and training such as:
• Preprocessing and cleaning data
• Feature selection
• ML model selection
• Hyper-parameter optimization
Auto AutoML
• Open source AutoML Toolkit (AMLT) created by Amazon AI.
• Easy to Use – Built-in Application
Auto AutoML
With AutoGluon, state-of-the-art ML results can be achieved in a few
lines of Python code.
Auto AutoML
With AutoGluon, state-of-the-art ML results can be achieved in a few
lines of Python code.

MLA-TAB-Lecture3-AutoGluon.ipynb
THANK YOU