STATISTICS AND DATA
ANALYSIS
z Livestream Workshop
@ Purwadhika
Sunday, 10 May 2020
Andre Nurrohman
andrenurrohman@gmail.com
z
Outline
Statistics and Data Analysis
Central Tendency
Measures of Variability
Visualizing Data
Distribution (Normal Distribution)
Hands On Session
z
Statistics and Data Analysis
Statistics is the science concerned with developing and studying methods for collecting,
analyzing, interpreting and presenting empirical data.
z
Statistics and Data Analysis
Types of Data
z
Statistics and Data Analysis
Statistics
Descriptive Inferential
Presenting, organizing, and Drawing conclusions about a
summarizing data population based data observed in
sample
z
Statistics and Data Analysis
Descriptive
Statistics
Central Measures
Tendency of Variability
Mean, median, and mode. Range, variance, standard
deviation, and quartile
z
Statistics and Data Analysis
Population
PARAMETER sampling
Statistical Inference Sample
STATISTIC
Parametric Methods
Nonparametric Methods
z
Statistics and Data Analysis
Parametric Method Nonparametric Method
Data Type Interval or Ratio Nominal or Ordinal
Assumed Distribution Normal Any
Assumed Variance Homogeneous Homo/Heterogeneous
Number of Data >= 30 Flexible
Data set relationship Independent Any
Usual central measure Means Medians
Statistical Power Strong Weak
Analysis Type
Independent measures, 2 groups Independet measure t test Mann-whitney test
Independent measures, >2 groups ANOVA Krusskal-Wallis test
Repeated measures, 2 conditions Matched pair t-test Wilcoxon test
z
Statistics and Data
Analysis
Data Analysis is the process of
systematically applying statistical
and/or logical techniques to describe
and illustrate, condense and recap,
and evaluate data.
Epicycle of Data Analysis
Source: The Art of Data Analysis
z
Central Tendency
Central
Tendency
Mean Median Mode
z
Central Tendency: Mean
Example:
Number of children in each house in my street:
0, 2, 3, 2, 1, 0, 0, 2, 0
Hence, the mean is:
(0+2+3+2+1+0+0+2+0) / 9 = 1.11
In my street, a new neighborhood with 11 children come in, so the
new mean is:
(0+2+3+2+1+0+0+2+0+11) / 10 = 2.1
z
Central Tendency: Median
Median is the middle data point.
1. Dataset is odd, exactly on the middle.
2. Dataset is even, average of the two middle data point.
Example:
0, 2, 3, 2, 1, 0, 0, 2, 0
Sort it Median:
0, 0, 0, 0, 1, 2, 2, 2, 3
1
0, 2, 3, 2, 1, 0, 0, 0, 11
Sort it 1.5
0, 0, 0, 0, 1, 2, 2, 2, 3, 11
z
Central Tendency: Mode
Mode is the most frequently occurs.
Example:
0, 2, 3, 2, 1, 0, 0, 2, 0
Count each value:
0 => 4
1 => 1
2 => 3
3 => 1
How’s the mode if we add 11?
z
Measures of Variability
Measures of Boxplot
Variability
Variance and
Range Standard Quartile Outliers
Deviation
z
Measures of Variability: Range
The distance between the largest value and
the smallest value of the data.
The range of the data: (1, 4, 5, 2, 8) is ???
z
Measures of Variability:
Variance and Standard Deviation
The variance is the average of the
squared differences from the mean.
The standard deviation is the square root of
the variance and is used to measure
distance from the mean.
z
Measures of Variability:
Quartile and Outlier
Q1 Q2 Q3
IQR = Q3 – Q1
Upper outliers > Q3 + 1.5 * IQR
Lower outliers < Q1 – 1.5 * IQR
Example:
(1, 4, 5, 2, 8)
Sort it
(1, 2, 4, 5, 8)
So, Q1 = 1.5 ; Q2 = 4 ; Q3 = 6.5
IQR = 6.5 – 1.5 = 5
Outliers > 6.5 + 1.5 * 5 = 14
Outliers < 6.5 – 1.5 * 5 = -1
z
Measures of Variability: Boxplot
z
Visualizing Data
Visualizing
Data
Frequency Proportion
Chart Histograms
Table Table
z
Visualizing Data: Tables
Frequency Table Proportion Table
z
Visualizing Data: Charts
z
Visualizing Data: Histogram
z
Skewness and Kurtosis
z
Normal Distribution
Probability distribution is a list of all of the possible outcomes of a random variable
along with their corresponding probability values.
Example:
A probability distribution of a fair 6-sided die.
Probability distribution function is a statistical function that describes all the possible
values and likelihoods that a random variable can take within a given range.
Most common example for probability distribution is Normal Distribution
z
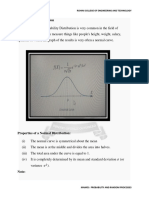
Normal Distribution
Properties of Normal Distribution:
1. The mean, mode and median are all
equal.
2. The curve is symmetric at the center
(i.e. around the mean).
3. Exactly half of the values are to the left
of center and exactly half the values
are to the right.
4. The total area under the curve is 1
z
TERIMAKASIH