Feedback Control Systems (FCS)
Lecture-18
Steady State Error
Dr. Imtiaz Hussain
email: imtiaz.hussain@faculty.muet.edu.pk
URL :http://imtiazhussainkalwar.weebly.com/
Introduction
• Any physical control system inherently suffers steady-
state error in response to certain types of inputs.
• A system may have no steady-state error to a step input,
but the same system may exhibit nonzero steady-state
error to a ramp input.
• Whether a given system will exhibit steady-state error for
a given type of input depends on the type of open-loop
transfer function of the system.
Classification of Control Systems
• Control systems may be classified according to
their ability to follow step inputs, ramp inputs,
parabolic inputs, and so on.
• The magnitudes of the steady-state errors due
to these individual inputs are indicative of the
goodness of the system.
Classification of Control Systems
• Consider the unity-feedback control system
with the following open-loop transfer function
• It involves the term sN in the denominator,
representing N poles at the origin.
• A system is called type 0, type 1, type 2, ... , if
N=0, N=1, N=2, ... , respectively.
Classification of Control Systems
• As the type number is increased, accuracy is
improved.
• However, increasing the type number
aggravates the stability problem.
• A compromise between steady-state accuracy
and relative stability is always necessary.
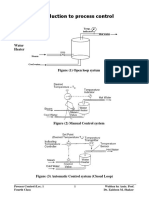
Steady State Error of Unity Feedback Systems
• Consider the system shown in following figure.
• The closed-loop transfer function is
Steady State Error of Unity Feedback Systems
• The transfer function between the error signal E(s) and the
input signal R(s) is
E( s ) 1
R( s ) 1 G( s )
• The final-value theorem provides a convenient way to find
the steady-state performance of a stable system.
• Since E(s) is
• The steady state error is
Static Error Constants
• The static error constants are figures of merit of control
systems. The higher the constants, the smaller the steady-
state error.
• In a given system, the output may be the position, velocity,
pressure, temperature, or the like.
• Therefore, in what follows, we shall call the output
“position,” the rate of change of the output “velocity,” and
so on.
• This means that in a temperature control system “position”
represents the output temperature, “velocity” represents
the rate of change of the output temperature, and so on.
Static Position Error Constant (Kp)
• The steady-state error of the system for a unit-step input is
• The static position error constant Kp is defined by
• Thus, the steady-state error in terms of the static position
error constant Kp is given by
Static Position Error Constant (Kp)
• For a Type 0 system
• For Type 1 or higher systems
• For a unit step input the steady state error ess is
Static Velocity Error Constant (Kv)
• The steady-state error of the system for a unit-ramp input is
• The static position error constant Kv is defined by
• Thus, the steady-state error in terms of the static velocity
error constant Kv is given by
Static Velocity Error Constant (Kv)
• For a Type 0 system
• For Type 1 systems
• For type 2 or higher systems
Static Velocity Error Constant (Kv)
• For a ramp input the steady state error ess is
Static Acceleration Error Constant (Ka)
• The steady-state error of the system for parabolic input is
• The static acceleration error constant Ka is defined by
• Thus, the steady-state error in terms of the static acceleration
error constant Ka is given by
Static Acceleration Error Constant (Ka)
• For a Type 0 system
• For Type 1 systems
• For type 2 systems
• For type 3 or higher systems
Static Acceleration Error Constant (Ka)
• For a parabolic input the steady state error ess is
Summary
Example#1
• For the system shown in figure below evaluate the static
error constants and find the expected steady state errors
for the standard step, ramp and parabolic inputs.
100( s 2 )( s 5)
R(S) C(S)
2
s ( s 8)( s 12)
-
Example#1 (Steady Sate Errors)
Kp Kv K a 10.4
0
0
0. 09
Example#1 (evaluation of Static Error Constants)
100( s 2)( s 5)
G( s )
s 2 ( s 8)( s 12)
K p lim G( s )
s 0 K v lim sG ( s )
s 0
100( s 2)( s 5)
K p lim 2 100s( s 2 )( s 5)
s 0 s ( s 8)( s 12) K v lim 2
s 0 s ( s 8)( s 12)
Kp
Kv
K a lim s 2G( s ) 100s 2 ( s 2)( s 5)
K a lim 2
s 0
s 0
s ( s 8 )( s 12 )
100( 0 2 )( 0 5)
K a 10. 4
( 0 8)( 0 12)
Example#8 (Lecture-16-17-18)
Figure (a) shows a mechanical vibratory system. When 2 lb of force
(step input) is applied to the system, the mass oscillates, as shown in
Figure (b). Determine m, b, and k of the system from this response
curve.
Example#8 (Lecture-22-23-24)
Figure (a) shows a mechanical vibratory system. When 2 lb of force
(step input) is applied to the system, the mass oscillates, as shown in
Figure (b). Determine m, b, and k of the system from this response
curve.
To download this lecture visit
http://imtiazhussainkalwar.weebly.com/
END OF LECTURES-18